Lacunary Generating Functions of Hybrid Type Polynomials in Viewpoint of Symbolic Approach

Nusrat Raza,Umme Zainab and Serkan Araci

1Mathematics Section,Women’s College,Aligarh Muslim University,Aligarh,202002,India

2Department of Mathematics,Aligarh Muslim University,Aligarh,202002,India

3Department of Economics,Faculty of Economics,Administrative of Social Sciences,Hasan Kalyoncu University,Gaziantep,TR-27410,Turkey

ABSTRACT In this paper,we introduce mon-symbolic method to obtain the generating functions of the hybrid class of Hermite-associated Laguerre and its associated polynomials.We obtain the series definitions of these hybrid special polynomials.Also,we derive the double lacunary generating functions of the Hermite-Laguerre polynomials and the Hermite-Laguerre-Wright polynomials.Further,we find multiplicative and derivative operators for the Hermite-Laguerre-Wright polynomials which helps to find the symbolic differential equation of the Hermite-Laguerre-Wright polynomials.Some concluding remarks are also given.

KEYWORDS Hermite-laguerre polynomials; laguerre-wright polynomials; hermite-laguerre-wright polynomials hermite-mittag-leffler functions

1 Introduction

Recently,it has been realized that the symbolic method of operational as well as umbral nature provides powerful tool for the study of special functions [1,2].Babusci et al.[3] developed the formalism of the symbolic method of operational nature for obtaining the generating functions of the Laguerre polynomials.By using symbolic method,the properties of the Laguerre polynomials could have accordingly been reduced to those of a Newton binomial containing an operator treated,in all the manipulations,as an ordinary algebraic quantity.Then Dattoli et al.[4]exploited symbolic method of umbral nature for obtaining the generating functions of the Hermite polynomials.

The Hermite and Laguerre polynomials,being orthogonal polynomial sequences,arise in various fields of engineering,mathematics and physics.The Hermite polynomials have applications in signal processing,probability,combinatorics,numerical analysis,quantum mechanics,random matrix theory,etc.These polynomials are also an example of Appell sequence,which obeys the umbral calculus.The Laguerre polynomials appear in quantum mechanics of the Morse potential,solution of the Schr¨odinger equation for a one-electron atom,oscillator system in phase space and 3D isotropic harmonic oscillator (see [5-8]),etc.The study of Laguerre polynomials becomes more convenient when these are expressed in terms of Laguerre-Wright polynomials.The symbolic method has emerged as a powerful tool to solve the problems involving certain special functions related to different branches of engineering and sciences for example fluid mechanics,physics,engineering and dynamical processes,etc.Most of the special functions do not show certain characteristics by classical methods and hence the importance of symbolic and umbral techniques are realized.These methods are widely used to establish numerous properties such as exponential and ordinary lacunary generating functions,symbolic definitions,symbolic differential equations,symbolic multiplicative and derivative operators etc.of known and new special functions and to evaluate various types of integrals involving these functions.A remarkable application of symbolic method is the convolution of two special functions to introduce and study new special functions.Motivated by the importance and applications of the Hermite and Laguerre-Wright polynomials and the usefulness of symbolic method,in this paper,we introduce and study the Hermite-Laguerre-Wright polynomials using symbolic method.

It has been shown that the concept related to monomiality techniques of the classical and generalized polynomials can be exploited to derive certain properties of families of polynomials,including Hermite and Laguerre polynomials used in pure and applied mathematics see for example [9,10].

The concept and formalism behind the monomiality principle and the symbolic methods can be exploited to introduce certain generalized as well as hybrid special polynomials and functions and to simplify the derivation of the properties of known and newly introduced special functions.The key element of this work is the introduction of the mon-symbolic method,which is the combination of monomiality techniques and symbolic method.

We recall that the ordinary Laguerre polynomialsLn(x)are defined by means of the following series definition [11]:

Babusci et al.have proved that the symbolic method of defining special functions can be exploited for obtaining several properties of certain special functions,which cannot be easily established by other well known methods [3].So this method filled a huge vacuum in the study of special functions.

Babusci defined a symbolic shift operatoras [3]:

which satisfies the propertyIn particular

In view of Eq.(1),the symbolic definition ofLn(x)is given as [3]:

Interchanging the variablesx→yandy→−xin the definition of Laguerre-Wright polynomials [3] the symbolic definition of the 2-variable Laguerre-Wright polynomials (2VLWP)(x,y)are as follows [3]:

which on simplifying,gives the following series definition for the 2VLWP(x,y)[3]:

The 2-variable associated Laguerre polynomials (2VALP)(x,y)are specified by means of the following series definition [12]:

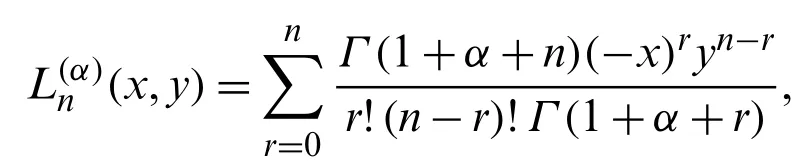
which in view of Eq.(6),gives [3]

where

In view of Eqs.(5),(7)and (8),symbolic definition of the 2VALP(x,y)is as follows [3]:

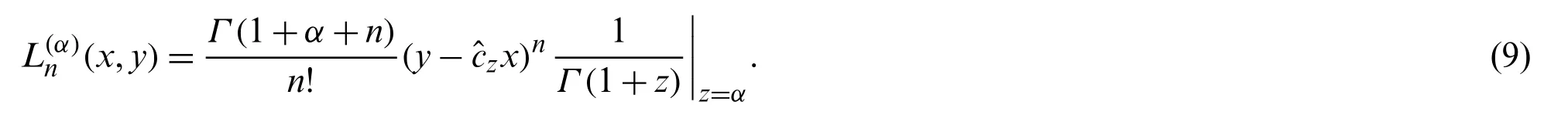
Fory=1,Eq.(5)gives the symbolic definition of the Laguerre-Wright polynomials (LWP)(x)in terms of operatoris as follows:

simplifying Eq.(10),we get the following series definition of LWP(x):

Next,we recall that the associated Laguerre polynomials (ALP)(x)are defined by the following series definition [11]:

In view of Eqs.(11)and (12),we have:

where

which in view of Eq.(10),gives:

In view of Eqs.(13)and (15),the symbolic definition of the ALP(x)is given as:

The symbolic definition of the Bessel-Wright functionWβ,α(x)is given as [3]:

which on simplifying,gives the following series definition ofWβ,α(x)[13,14]:

The symbolic definition of the Mittag-Leffler functionEβ,α(x)is given as [3]:

which on simplifying,gives the following series definition ofEβ,α(x)[13,14]:

The study of Hermite polynomials help to solve the classical boundary-value problems in the parabolic regions,through the use of parabolic coordinates and in quantum mechanics as well as in other areas of sciences.We recall that the 2-variable Hermite Kampe de Feriet polynomials(2VHKdFP)Hn(x,y)are defined by means of the following generating function and series definition [15]:

respectively.

Next,we recall that thenth-order Bessel functionJn(x)is defined by the following series definition [16]:

In view of Eq.(23)forn= 0,the 0th-order Bessel functionJn(x)is defined as [17]:

According to the monomi ality principle proposed by Steffensen [18] and developed by Dattoli [10],a polynomial setis called quasi-monomial if there exist two operators multiplicative operatorand derivative operator,respectively,such that [10]:

and

The multiplicative operatorand derivative operatorsatisfy the following commutation relation:

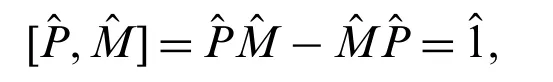
Some characteristics are as follows:

(ii)Assuming here and in the followingp0(x)= 1,thenpn(x)can be explicitly constructed as:

which gives the series definition forpn(x).

(iii)Consequently the generating function ofpn(x)can be obtained as:

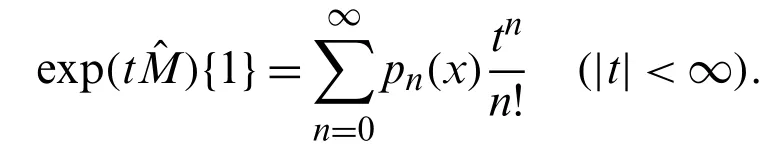
By induction,Eq.(25)gives:

We recall that the 2VHKdFPHn(x,y)is quasi-monomial with respect to the following multiplicative and derivative operators [10]:

respectively.

In view of Eq.(22),it can be easily verified that [10]:

Dattoli et al.[4] used the transition of 2VHKdFPHn(x,y)from monomiality to umbral interpretation.The newton binomial realizes the umbral image of 2VHKdFPHn(x,y).Dattoli et al.[4]have proved that the operational method become a fairly powerful tool once complimented with a notation of umbral nature.The umbral approach to the 2VHKdFPHn(x,y)is particularly useful for a straightforward derivation of the relevant properties.

Dattoli redefined the 2VHKdFPHn(x,y)using umbral approach of symbolic method as [4]:

which forr=0,givesφ0=1.Thus Eq.(33)can be rewritten as:

In view of Eqs.(28)and (35),we get the following symbolic multiplicative operator of 2VHKdFP:

The use of umbral formalism looks much promising to develop a new technique to study the theory of special polynomials and special functions as well.Hybrid special functions as well as polynomials and their applications has been recognized by Dattoli and his co-workers [2,9,12].

After you had gone away, said she, they tried to make me learn how to govern the kingdom, which wearied me to death, so that I begged and prayed Lolotte to take me away with her, and this she presently did, but very reluctantly

We recall that the 2-variable Hermite-Laguerre polynomials (2VHLP)HLn(x,y)are defined by means of the following series definition [9]:

and the Hermite-Bessel-Wright function (HBWF)HWβ,α(x,y)is defined by means of the following series definition [3]:

Motivated by the work of Babusci and his co-authors on lacunary generating functions for Laguerre polynomials [3] and application of the Laguerre polynomials [12,19,20],in this paper,we introduce certain generating functions for the 2-variable Hermite-Laguerre polynomials and some new families of polynomials.In Section 2,we introduce the Hermite-associated Laguerre polynomials and obtain ordinary generating function via mon-symbolic approach.Further,we define some new families of polynomials such as Hermite-Laguerre-Wright polynomials and find their exponential and ordinary generating functions.In Section 3,we derive the double and the triple lacunary 2-variable Hermite-Laguerre polynomials and find double lacunary generating functions for the 2-variable Hermite-Laguerre polynomials and the Hermite-Laguerre-Wright polynomials.In Section 4,we proposed an idea to find multiplicative and derivative operators for Hermite-Laguerre-Wright polynomials which helps to find symbolic differential equation for the same polynomials.

2 Generating Functions of the Hermite-Associated Laguerre and Hermite-Laguerre-Wright Polynomials

The most interesting example to understand the flexibility and usefulness of the symbolic method is derivation of generating functions of special polynomials and special functions as well.In this paper,we consider two types of generating functions,namely exponential and ordinary.

In this section,we introduce the Hermite-associated Laguerre polynomials and the Hermite-Laguerre-Wright polynomials by using the mon-symbolic method.Also,we obtain certain generating functions of these polynomials.

In view of Eqs.(15)and (36),we introduce the 1-parameter Hermite-Laguerre-Wright polynomials (1PHLWP)H(x,y)by means of the following symbolic definition:

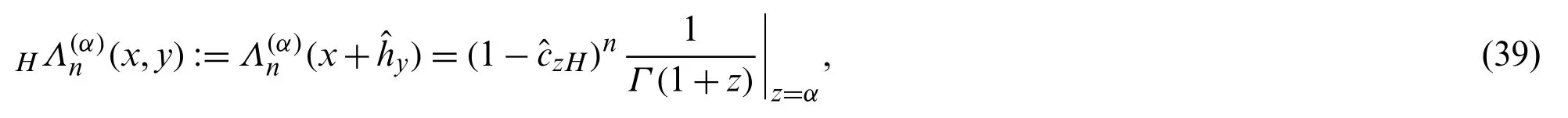
where

Since,in view of Eqs.(35)and (40),we have:

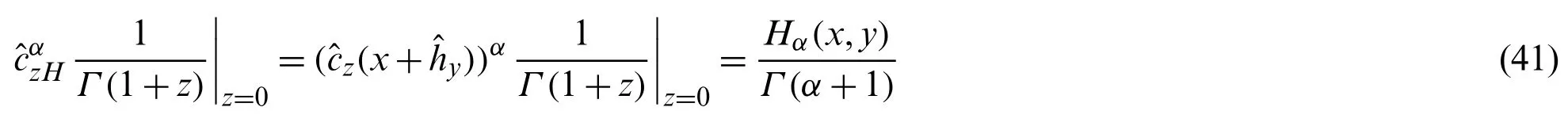
and

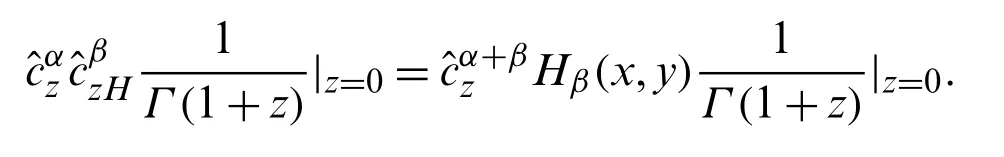
Binomially expanding the right hand side of Eq.(39)and then using Eqs.(35)and (40),we have:

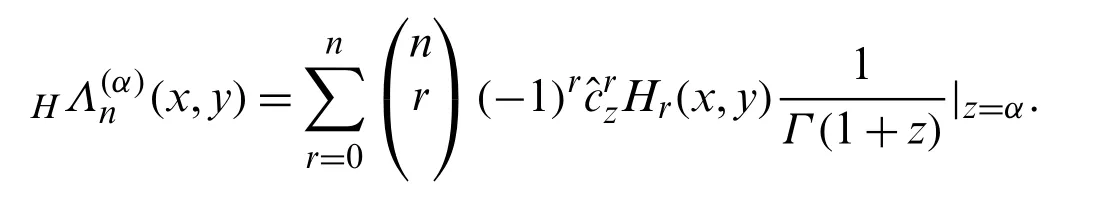
Simplifying,we get the following series definition of the 1PHLWP(x,y):

Now,in view of Eq.(39),we define the Hermite-associated Laguerre polynomials (HALP)(x,y)by replacingxwith(x+)in Eq.(13)as:

Next,we define the Hermite-Laguerre-Wright polynomials (HLWP)(x,y)by replacingxwith(x+)in Eq.(10)as:

which on using Eq.(35),gives the following series definition of(x,y):

In view of Eqs.(42)and (45),it is clear that:

In the recent years,Dattoli used the monomiality principle to find the generating functions for some special polynomials and special functions as well [9,10,12].Also,Babusci et al.[3] used the concept of symbolic method to find the generating function of the Laguerre Polynomials.In this paper,we combine the symbolic method with the monomiality technique to obtain the generating functions of the HALP(x,y)and the HLWP(x,y).

Now,we establish following result for the ordinary generating function of the HALP(x,y):

Theorem 2.1The ordinary generating function for HALP(x,y)is given by:

Proof.From Eq.(43),we have:

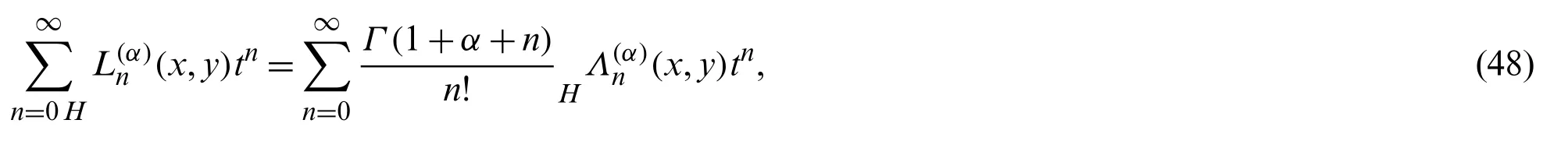
which on using Eqs.(44)and (46)in the right hand side,it gives:

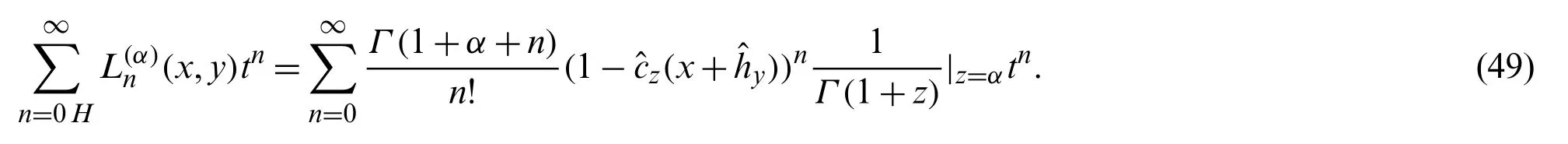
Using the following relation between Gamma function and pochhammer symbol:

in Eq.(49),we find:

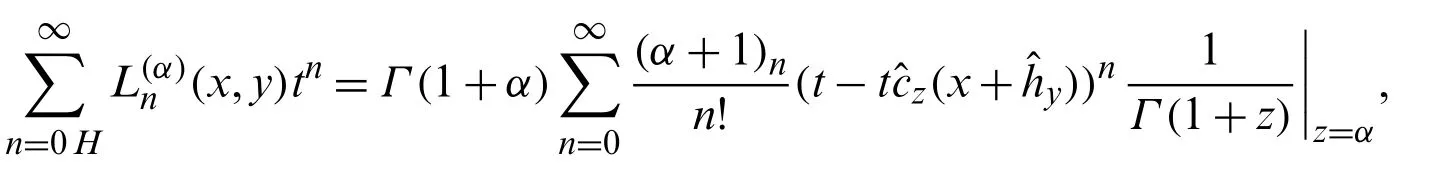
which on using the following series expansion:

gives:

Again,using Eqs.(50)and (51),we have:

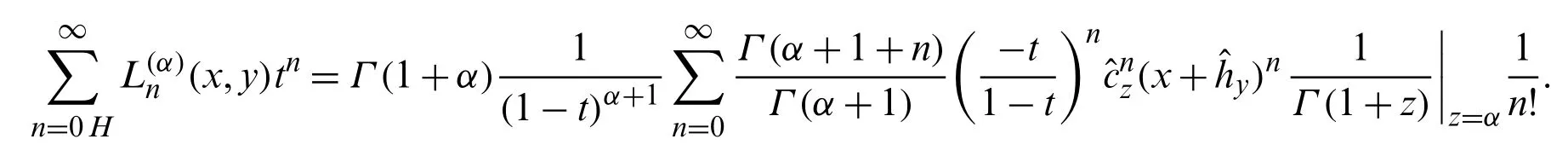
Using Eq.(35)in the right hand side of the above equation,we have:

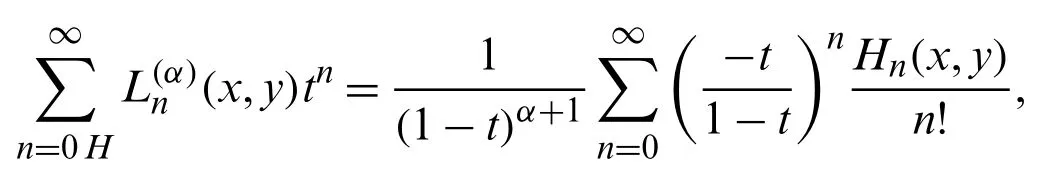
which on using Eqs.(21)and (32)gives assertion (47).

Next,we establish following result for the exponential generating function of the HLWP(x,y):

Theorem 2.2The exponential generating function for HLWP(x,y)is given by:

Proof.Using Eq.(44),we have:

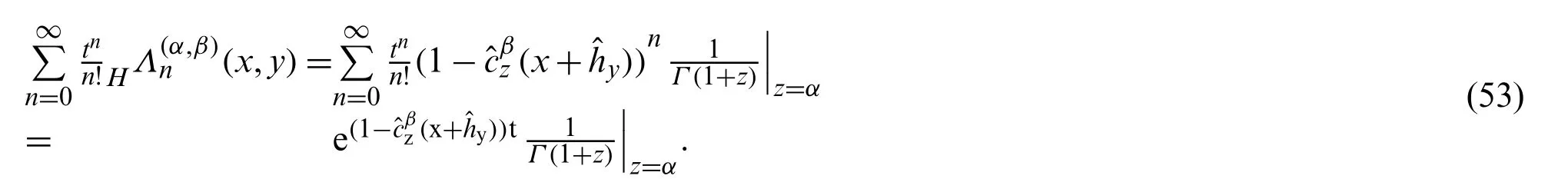
We find:

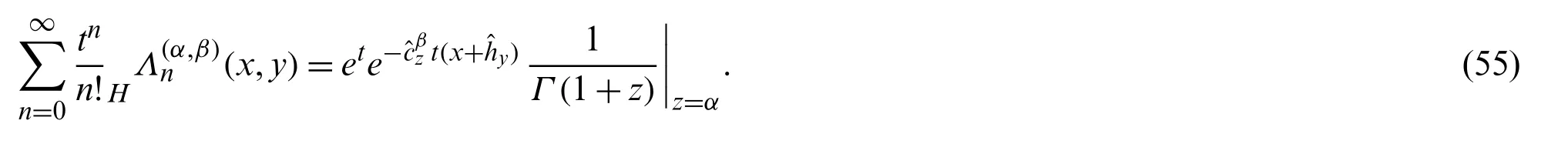
Now,expanding the second exponential in the right hand side of the above equation,Eq.(55)yields:

which on simplifying,gives:

Using Eq.(32)in Eq.(56),we have:

which in view of Eq.(38),yields assertion (52).

Since,in view of Eqs.(43)and (46),

Therefore,from Theorem 2.2,we get the following result.

Corollary 2.1The ordinary generating function for the polynomialis given by:

Now,we proceed to obtain the ordinary generating function for the HLWP(x,y).For obtaining the ordinary generating function for the HLWP(x,y),we define the Hermite-Mittag-Leffler function (HMLF)HEβ,α(x,y)by replacingxwith(x+)in Eq.(19)as:

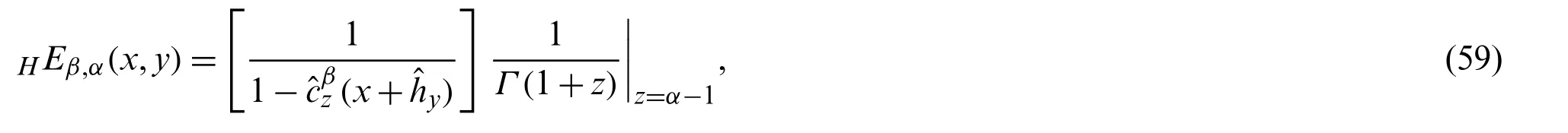
which on simplifying and then using Eq.(35),gives the following series definition for theHEβ,α(x,y):

Now,we establish following result for the ordinary generating function of the HLWP(x,y):

Theorem 2.3The ordinary generating function for HLWP(x,y)is given by:

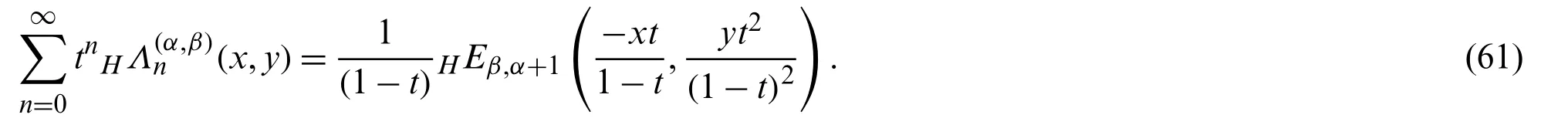
Proof.From Eq.(44),we have:

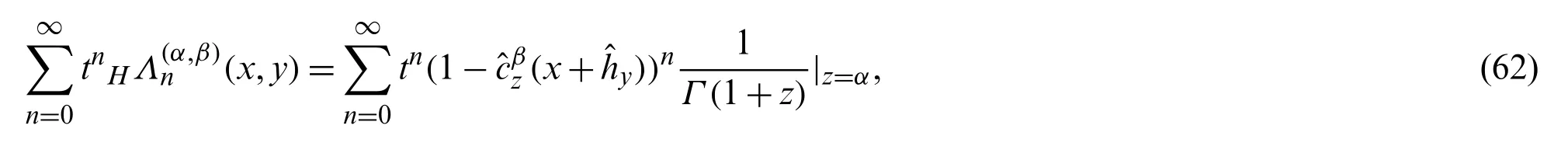
which on using Eq.(51)forα= 1,gives:

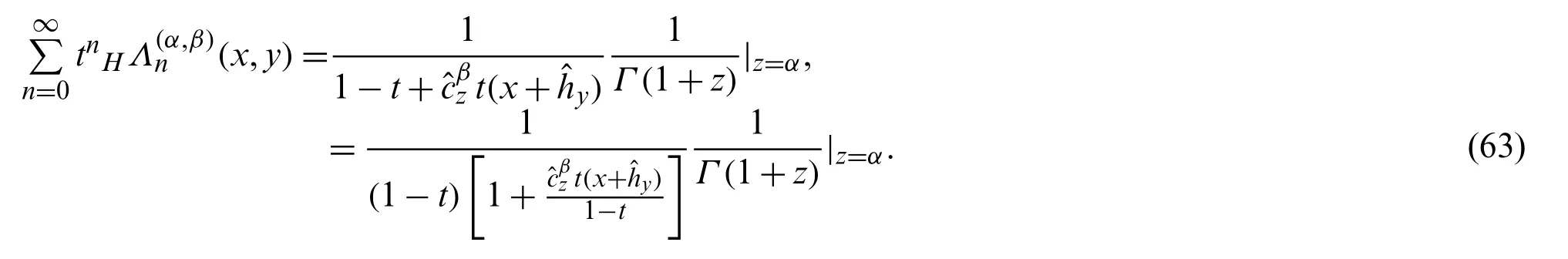
In view of Eq.(51)forα= 1,we find:

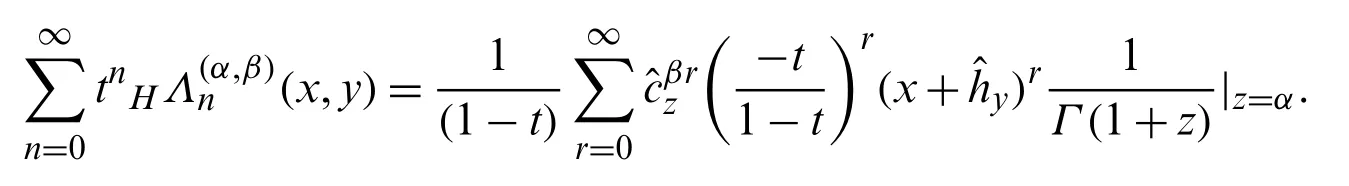
Using Eqs.(32)and (35)in the above equation,we have:

which in view of Eq.(60),gives assertion (61).

Now,we list the following examples of the special polynomials introduced or discussed in this paper.

In the next section,we obtain the lacunary generating functions of the Hermite-Laguerre polynomialsHLn(x,y)and the HLWP(x,y).

3 Lacunary Generating Functions

Babusci et al.redefined the Laguerre polynomials of degrees 2nand 3n(n∈N)by means of the series definitions and obtained the generating functions for these polynomials by using the symbolic method [3].The generating functions of the Laguerre polynomials of degrees 2nand 3n(n∈N)are named double and triple lacunary generating functions,respectively.Recently,Dattoli et al.[4] obtained the double lacunary generating function of the 2VHKdFPHn(x,y).

In this section,we define the 2-variable Hermite-Laguerre polynomialsHL2n(x,y)andHL3n(x,y)by using the symbolic method.Also,we obtain double lacunary generating functions for the 2VHLP and the HLWP.

In the case whenα= 0 in Eq.(43),the associated Laguerre polynomials(x)reduce to the Laguerre polynomialsLn(x)as follows:

which in view of Eqs.(39)and (40),gives the following symbolic definition of the 2VHLPHLn(x,y):

Now,we give the following theorem for the 2-variable Hermite-Laguerre polynomialsHL2n(x,y)andHL3n(x,y).

Theorem 3.1The series definition forHL2n(x,y)andHL3n(x,y)are given by:

and

Proof.In view of Eq.(64),we have:

which on simplifying,gives:

Using Eq.(39)in the right hand side of the above equation,we find:

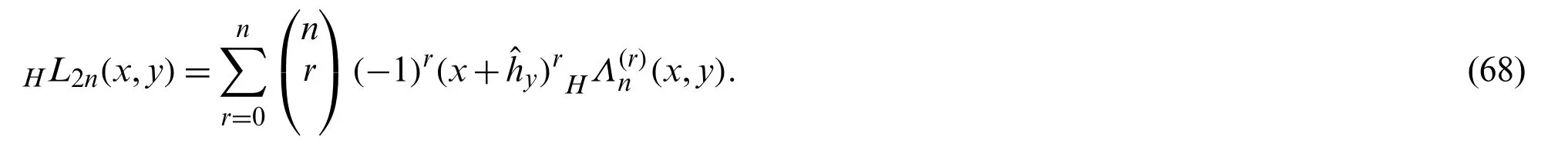
Therefore,in view of Eqs.(35)and (42),we have:

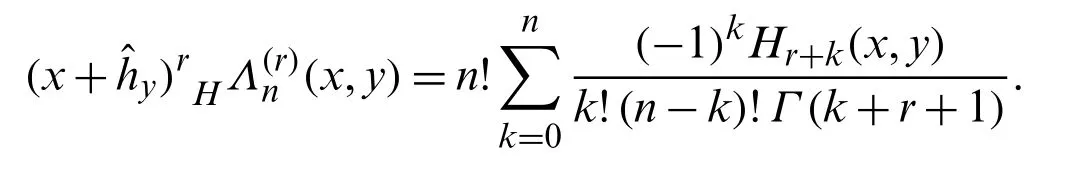
If we denotexr(x)by the polynomial(x),then by replacingxwith(x+),we find:

which on using Eq.(39),gives the following symbolic definition of the(x,y):

Thus,using Eq.(69)in Eq.(68),we get the assertion (65).

By the same way,we can prove it forHL3n(x,y),given by (66).

Now,we proceed to obtain the double lacunary generating function of the 2VHLPHLn(x,y).For this,we denote the product of two 2VHKdFPHn(x,y)andHn(z,w),byH2n(x,y;z,w)which are called Bi-Hermite polynomials.

Thus,in view of Eq.(33),we have:

Now,we define the Bi-Hermite-Bessel functionH2J0(x,y;z,w)as:

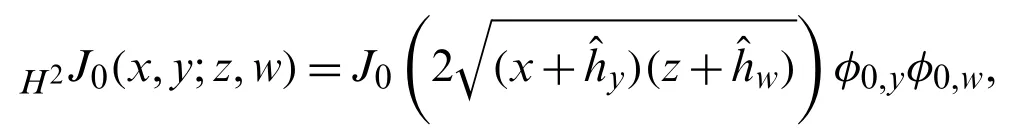
which on using Eq.(24),gives:

In view of Eq.(33),we get the following series definition ofH2J0(x,y;z,w):

Now,we are in a position to state the following theorem:

Theorem 3.2The double lacunary generating function for 2VHLPHLn(x,y)is given by:

whereH2J0(x,y; 2t,t)denotes the Bi-Hermite-Bessel function.

Proof.In view of Eq.(67),we have:

which becomes:

Simplifying the above equation,we find:

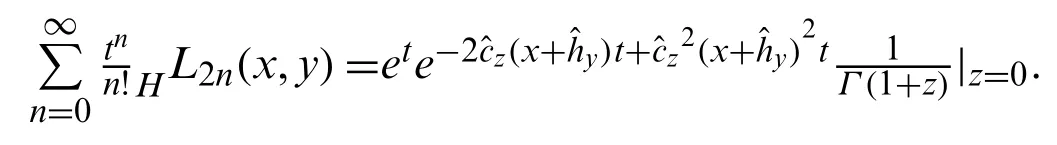
Using Eq.(21)in the above equation,we obtain:

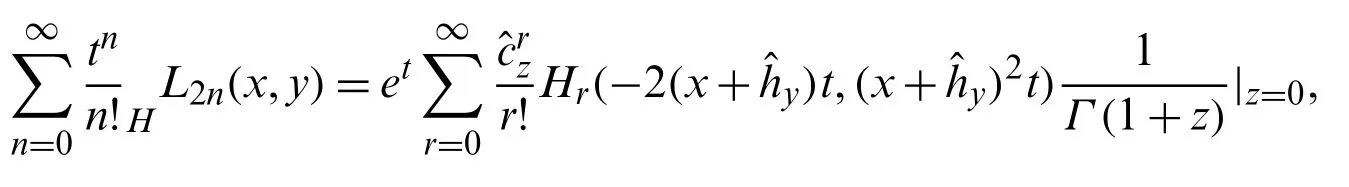
which on using Eqs.(32)and (35),it gives:

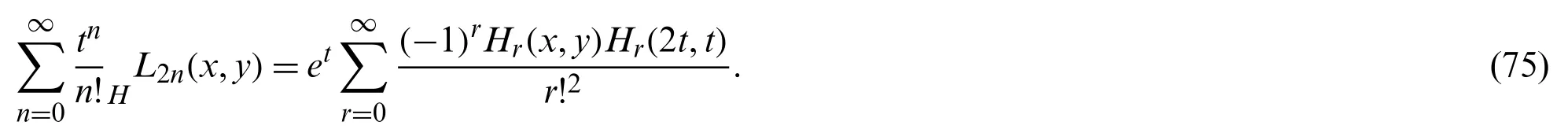
In view of Eqs.(72)and (75),we get assertion (73).

Similarly,to obtain the double lacunary generating function for the HLWP(x,y),we define the Bi-Hermite-Wright function (BHWF)H2Wβ,α(x,y;z,w)as:

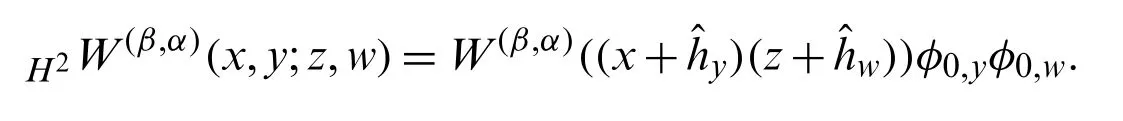
Using Eq.(18)in the right hand side of the above equation,we have:

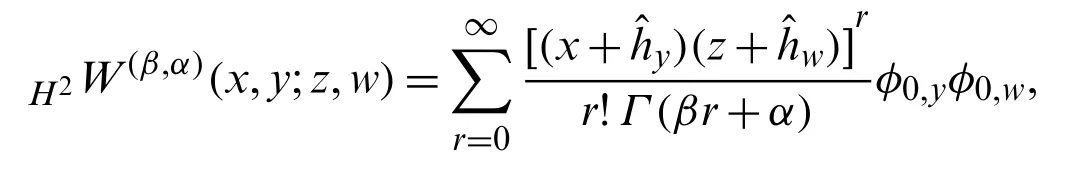
which on using Eq.(33),gives the following series definition ofH2W(β,α)(x,y;z,w):

We,now state the following theorem:

Theorem 3.3The double lacunary generating function for HLWP(x,y)is given by

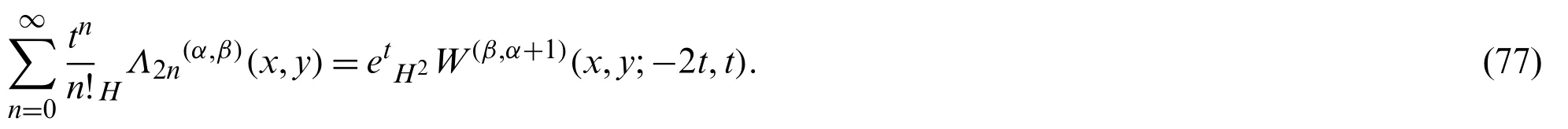
Proof.Using Eq.(44),we have

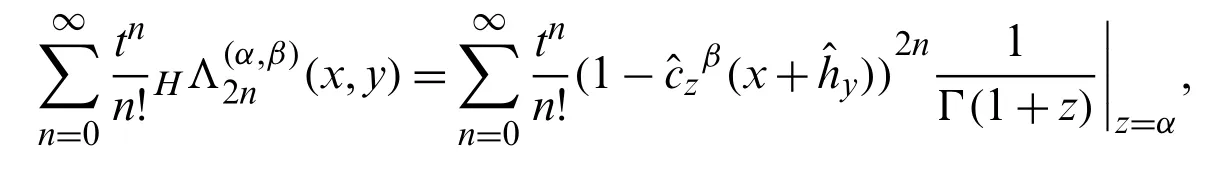
which can be written as:

which on using Eq.(21),gives:

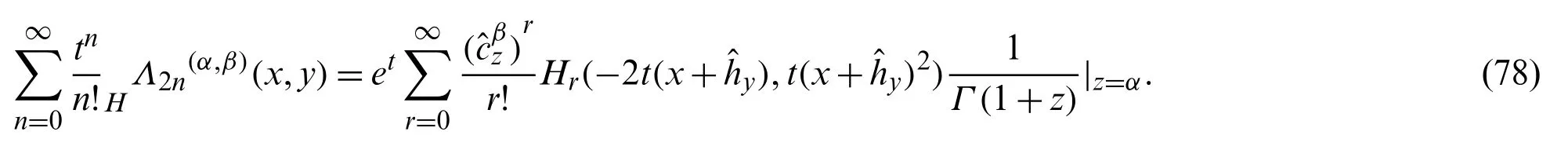
In view of Eqs.(32)and (35),we have:

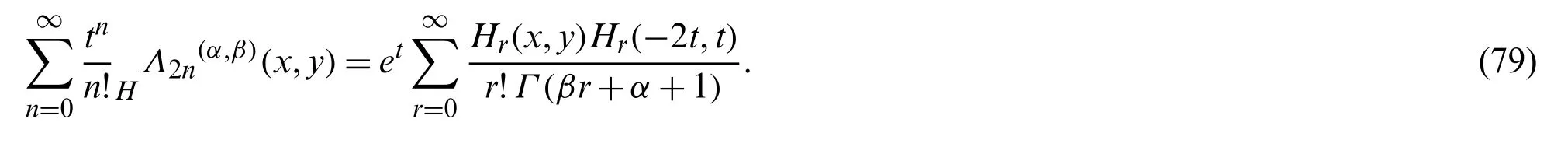
Using Eq.(76)in the right hand side of (79),we get assertion (77).

In the next section,we introduce the symbolic multiplicative and derivative operators and establish the symbolic differential equation for HLWP(x,y)by using the monomiality method.

4 Monomiality Principle and Symbolic Differential Equation

In this section,we develop the theory of symbolic multiplicative and derivative operators for the HLWP(x,y),which helps to find the symbolic differential equation for the HLWP(x,y).

We obtain the following symbolic-differential recurrence relation for HLWP(x,y):

Theorem 4.1The HLWP(x,y)satisfies the following recurrence relation:

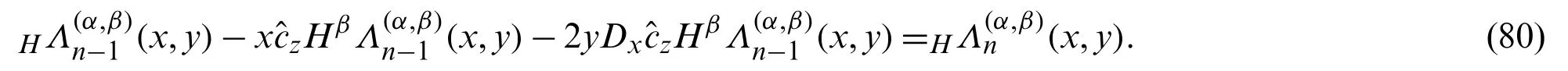
Proof.Using Eqs.(30)and (36)in Eq.(44),we have:

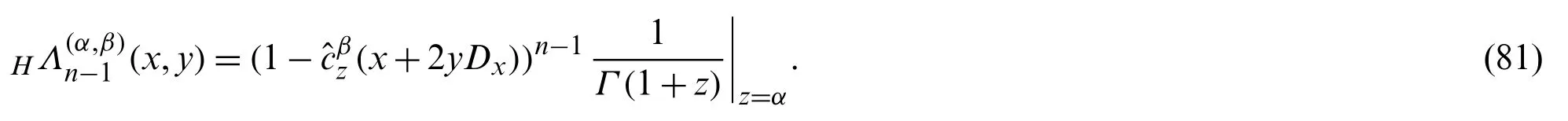
Operating(1 −(x+2yDx))on both sides of Eq.(81),and then using Eqs.(36)and (44),we obtain:

which on simplifying,gives assertion (80).

Now,we obtain the symbolic multiplicative and derivative operators for the HLWP(x,y).

Theorem 4.2The HLWP(x,y)is quasi-monomial with respect to the following symbolic multiplicative and derivative operators:

and

respectively.

Proof.Using Eqs.(30)and (36)in Eq.(44),we have:

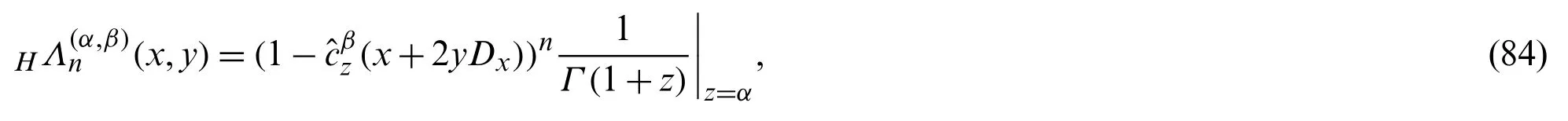
Now,operating(1 −(x+2yDx))in the both sides of Eq.(84),we have:

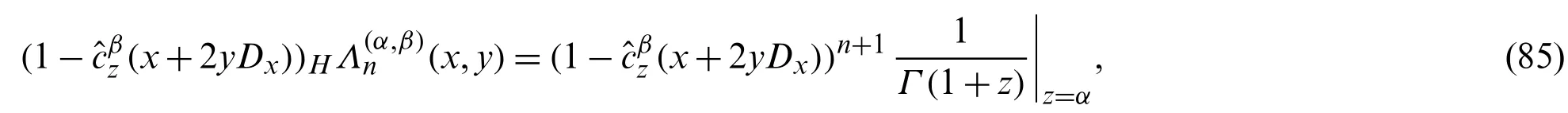
which on using (84),gives:

In view of Eqs.(25)and (86),we obtain assertion (83a).

Now,differentiating Eq.(45)partially with respect tox,we have:

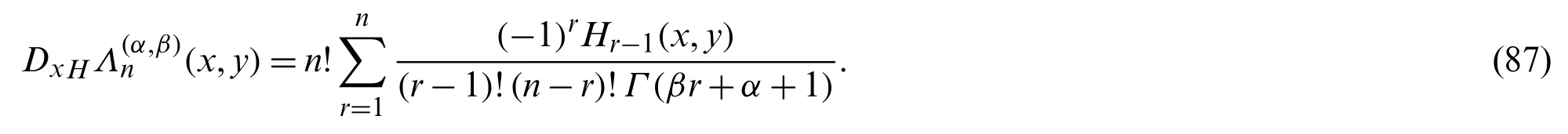
Replacingrbyr+ 1 and operatingon both sides of the above equation,we have:

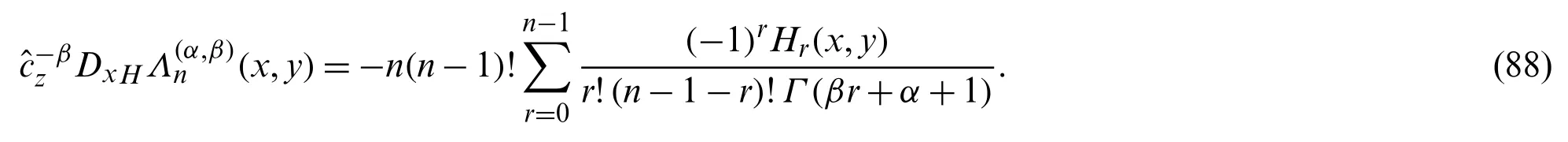
Using Eq.(45),we get:

which in view of Eq.(26),we get assertion (83b).

Further,we establish the following theorem for the HLWP(x,y):

Theorem 4.3The HLWP(x,y)satisfies the following symbolic differential equation:

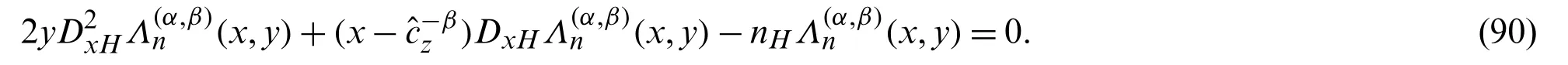
Proof.Using multiplicative and derivative operators given by Eqs.(83)and (84)in Eq.(27),we find:

which on simplification,gives assertion (90).

5 Concluding Remarks

It has been realized that the symbolic method serves as a useful tool to introduce several special polynomials and their lacunary forms.In this paper,we used the symbolic method to find the generating functions of different polynomials.In this section,we define the 2-parameter,2-variable Laguerre polynomials (2P2VLP)by using symbolic approach.

We introduce the 2-parameter,2-variable Laguerre polynomials (2P2VLP)(x,y)by means of the symbolic definition.

In view of Eqs.(13)and (14),we define the 2P2VLP(x,y)as:

which on using Eq.(5),gives the following symbolic definition of the 2P2VLP(x,y):

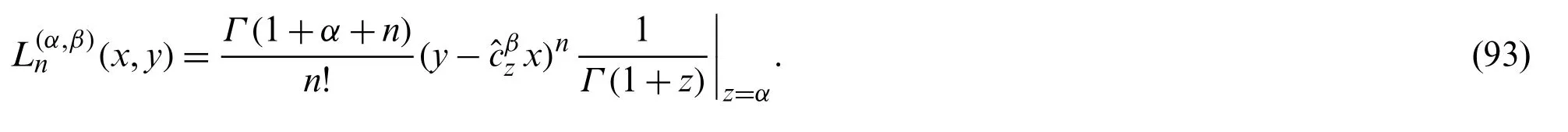
Using Eq.(11)in Eq.(93),we get the following series definition of the 2P2VLP(x,y):

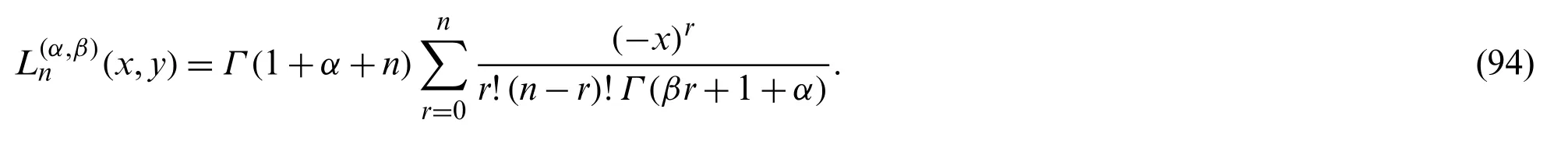
Finding generating functions of this polynomial is an open problem for further research.

The results established in this paper can also be obtained by using the umbra of 2VHKDFPHn(x,y)but the method will not be purely symbolic.We conclude this paper with the fact that the symbolic method makes study of special functions easier than classical techniques.

We are now in a position to conclude our paper by investigating the special cases for our main equations which was given below as Table 1.

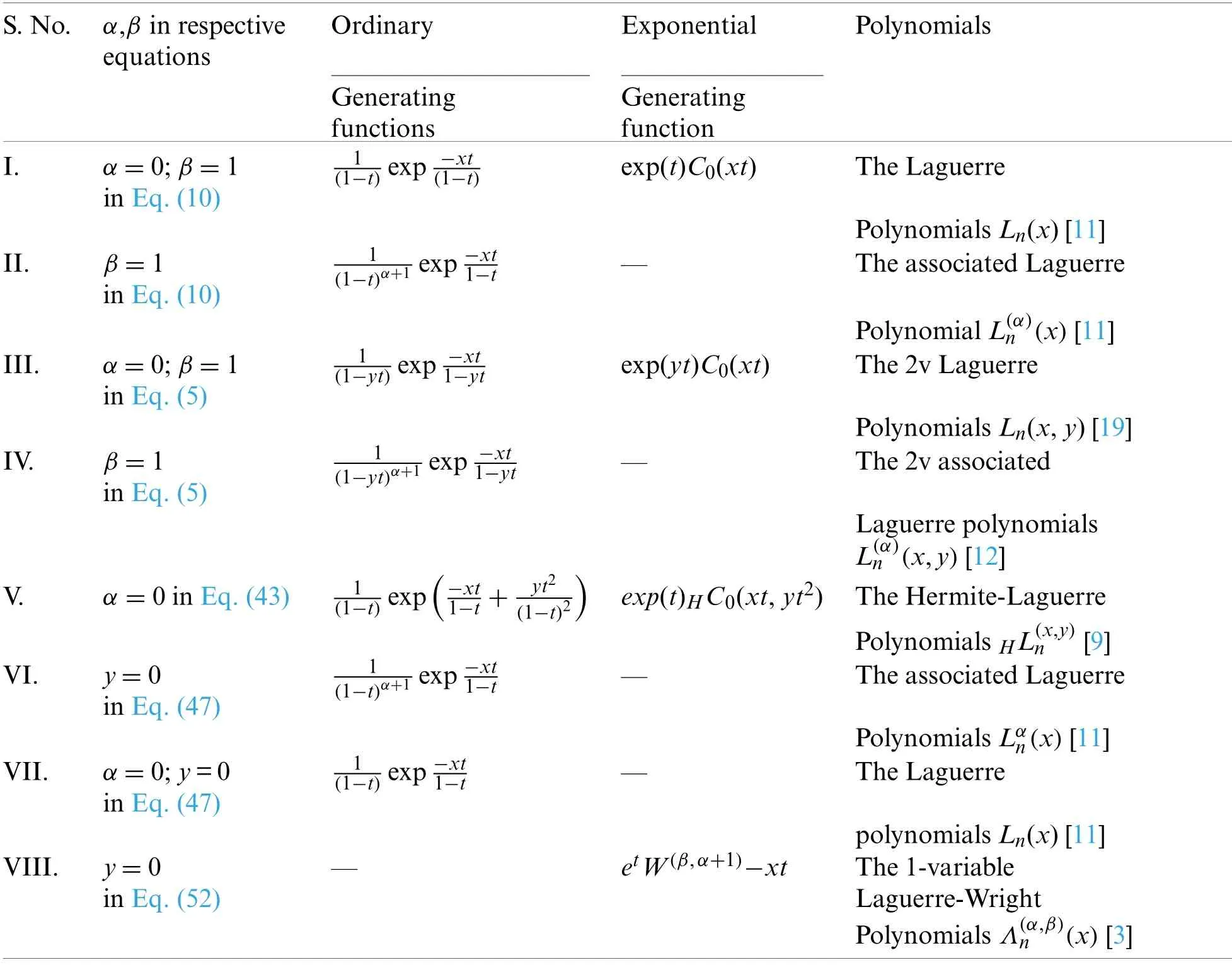
Table 1:Examples

Acknowledgement:The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that there are no conflicts of interest regarding the publication of this paper.