Some Formulas Involving Hypergeometric Functions in Four Variables

Hassen Aydi,Ashish Verma,Jihad Younis and Jung Rye Lee

1Universit´e de Sousse,Institut Sup´erieur D’Informatique et,Des Techniques de Communication,H.Sousse,4000,Tunisia

2Department of Mathematics and Applied Mathematics,Sefako Makgatho Health Sciences University,Ga-Rankuwa,South Africa

3China Medical University Hospital,China Medical University,Taichung,40402,Taiwan

4Department of Mathematics,V.B.S.Purvanchal University,Jaunpur,222003,India

5Department of Mathematics,Aden University,Khormaksar,P.o.Box 6014,Yemen

6Department of Data Science,Daejin University,Kyunggi,11159,Korea

ABSTRACT Several(generalized)hypergeometric functions and a variety of their extensions have been presented and investigated in the literature by many authors.In the present paper,we investigate four new hypergeometric functions in four variables and then establish several recursion formulas for these new functions.Also,some interesting particular cases and consequences of our results are discussed.

KEYWORDS Recursion formula; quadruple hypergeometric functions; pascal; identity

1 Introduction

In recent years,many researchers introduced and studied several extensions and generalizations of various special functions due to its applications in diverse areas of mathematical,physical,engineering,etc.Agarwal et al.[1,2] established some properties for generalized Gauss hypergeometric functions,which were introduced by Özergin et al.Later,Agarwal et al.[3] and Çetinkaya et al.[4] introduced and investigated further extensions of Appell’s hypergeometric functions of two variables and Lauricella’s hypergeometric functions of three variables by using the generalized Beta type function.Purohit et al.[5] investigated Chebyshev type inequalities involving fractional integral operator containing a multi-index Mittag-Leffler function in the kernel.Suthar et al.[6]introduced certain generalized forms of the fractional kinetic equation pertaining to the (p,q)-Mathieu-type power series using the Laplace transforms technique.Chandola et al.[7] defined a new extension of beta function using the Appell series and the Lauricella function.The interested reader may be referred to several recent papers on the subject (see,e.g.,[8-11] and the references cited therein).

Hypergeometric functions in several variables have many applications in applied problems (see,e.g.,[12-16]).Also,multidimensional hypergeometric functions are used to solve boundary value problems (Dirichlet problem,Neumann problem,Holmgren problem,etc)for multidimensional degenerate differential equations (see [17-19]).In [20],Exton defined twenty one complete hypergeometric functions in four variables denoted by the symbolsK1,K2,...,K21.In [21],Sharma et al.introduced eighty three complete quadruple hypergeometric functions,namelyVery recently,Younis et al.[22] introduced and studied further quadruple hypergeometric functions denoted byEach quadruple hypergeometric function in [20-22] is of the form:

whereΔ(m,n,p,q)is a certain sequence of complex parameters and there are twelve parameters in each seriesX(4)(.)(eighta′sand fourc′s).The 1st,2nd,3rd and 4th parameters inX(4)(.)are connected with the integersm,n,pandq,respectively.Each repeated parameter in the seriesX(4)(.)points out a term with double parameters inδ(m,n,p,q).For example,X(4)(σ1,σ1,σ2,σ2,σ3,σ3,σ4,σ5)mean that (σ1)m+n(σ2)p+q(σ3)m+n(σ4)p(σ5)qincludes the term.Similarly,X(4)(σ1,σ1,σ1,σ2,σ1,σ1,σ2,σ3)points out the term (σ1)2m+2n+p(σ2)p+q(σ3)qandX(4)(σ1,σ1,σ2,σ4,σ1,σ2,σ3,σ5)shows the existence of the term (σ1)2m+n(σ2)n+p(σ3)p(σ4)q(σ5)q.Thus,it is possible to form various combinations of indices.There seems to be no way of establishing independently the number of distinct Gaussian hypergeometric series for any given integern≥2 without stating explicitly all such series.Thus,in every situation withn= 4,one ought to begin by actually constructing the set just as in the casen= 3 (see [23]).Motivated by the works [20-22],we decide to define further hypergeometric functions in four variables as follows:

where

Here,C,Z−0and N denote the sets of complex numbers,non-positive integers,and positive integers,respectively.

Recently,many authors have obtained several recursion formulas involving hypergeometric functions in several variables.In Opps et al.[24],introduced the recursion formulas for the Appell’s functionF2and gave its applications to radiation field problems.Wang [25] presented the recursion formulas for Appell functionsF1,F2,F3andF4.Sahai et al.[26,27] established the recursion formulas for Lauricella’s triple functions,Srivastava hypergeometric functions in three variables,k-variable Lauricella functions and the Srivastava-Daoust and related multivariable hypergeometric functions.Shehata et al.[28] discussed and derived new recursion relations for the Horn’s hypergeometric functions.In this present paper,we aim to establish several recursion formulas for the new hypergeometric functions in four variables defined by (1.1)-(1.4).

The following abbreviated notations are used in this paper.We,for example,writefor the series(σ1,σ1,σ2,σ4,σ1,σ2,σ3,σ5;ρ1,ρ1,ρ2,ρ1;x,y,z,u)and(σ1+n)for(σ1+n,σ1+n,σ2,σ4,σ1,σ2,σ3,σ5;ρ1,ρ1,ρ2,ρ1;x,y,z,u).The notation1+n,σ2+n1)stands for(σ1+n,σ1+n,σ2+n1,σ4,σ1+n,σ2+n1,σ3,σ5;ρ1,ρ1,ρ2,ρ1;x,y,z,u)and(σ1+n,σ2+n1,ρ1+n2)stands for(a1+n,σ1+n,σ2+n1,σ4,σ1+n,σ2+n1,σ3,σ5;ρ1+n2,ρ1+n2,ρ2,ρ1;x,y,z,u),etc.

2 Main Results

Here,we establish several recursion formulas for our hypergeometric functions in four variables.

Theorem 2.1The following recursion formulas hold true for the numerator parameterσ1,σ2,σ3,σ4,σ5of the:

Proof.From the definition of the hypergeometric functionand the relation

we obtain the following contiguous relation:

To find a contiguous relation for(σ1+2),we replaceσ1byσ1+1 in (16)and simplify.This leads to:

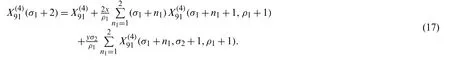
Iterating this processn-times,we obtain (5).For the proof of (6),replace the parameterσ1byσ1−1 in (15).This implies that

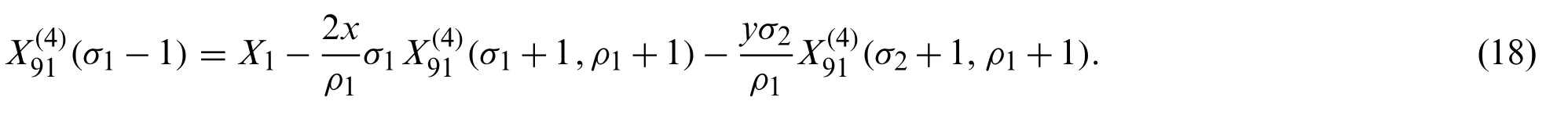
Iteratively,we get (6).

The recursion formulas from (7)-(14)can be proved in a similar manner.

Theorem 2.2The following recursion formulas hold true for the numerator parameterσ2,σ3,σ4,σ5of theX(4)91 :

Proof.The proof of (19)is based upon the principle of a mathematical induction onn∈N.Forn=1,the result (19)is true obviously following (7).Suppose (19)is true forn=m,that is,

Replacingσ2withσ2+1 in (27)and using the contiguous relation (7)forn=1,we get

By a simplification,(28)takes the form

Using the Pascal’s identity in (29),we have

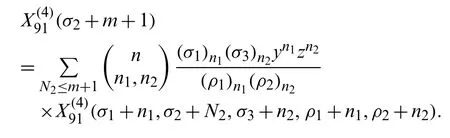
This establishes (19)forn=m+ 1.Hence,by induction,the result given in (19)is true for all values ofn.The recursion formulas (20)-(26)can be proved in a similar manner.

Theorem 2.3The following recursion formulas hold true for the denominator parameterρ1,ρ2of the:

Proof.Applying the definition of the hypergeometric functionand the relation

we have:

Using this contiguous relation to thewith the parameterρ1−nforn-times,we get the result (30).The recursion formula (31)can be proved in a similar manner.

Theorem 2.4The following recursion formulas hold true for the numerator parameterσ1,σ2,σ3,σ4,σ5of the

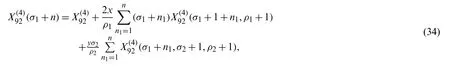
Theorem 2.5The following recursion formulas hold true for the numerator parameterσ2,σ3,σ4,σ5of the

whereN2=n1+n2.

Theorem 2.6The following recursion formulas hold true for the denominator parameterρ1,ρ2of the

Theorem 2.7The following recursion formulas hold true for the numerator parameterσ1,σ2,σ3,σ4,σ5of the

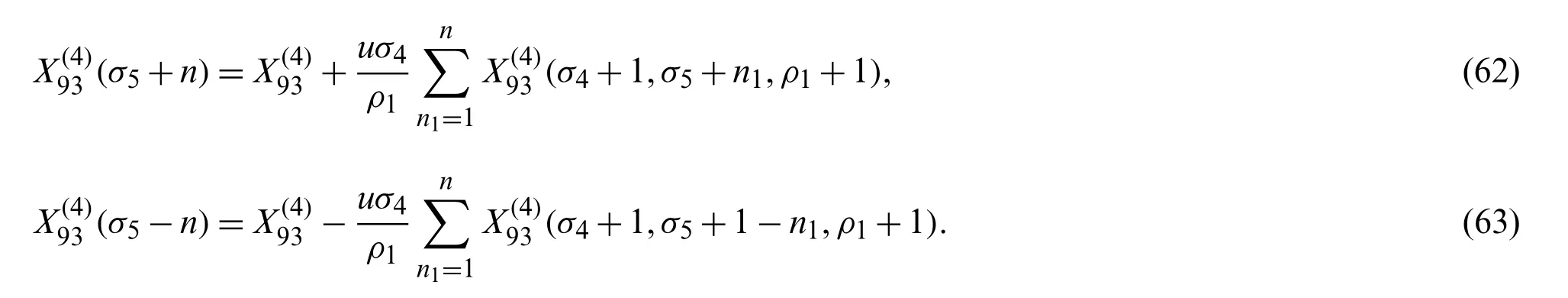
Theorem 2.8The following recursion formulas hold true for the numerator parameterσ2,σ3,σ4,σ5of the

whereN2=n1+n2.

Theorem 2.9The following recursion formulas hold true for the denominator parameterρ1,ρ2of the

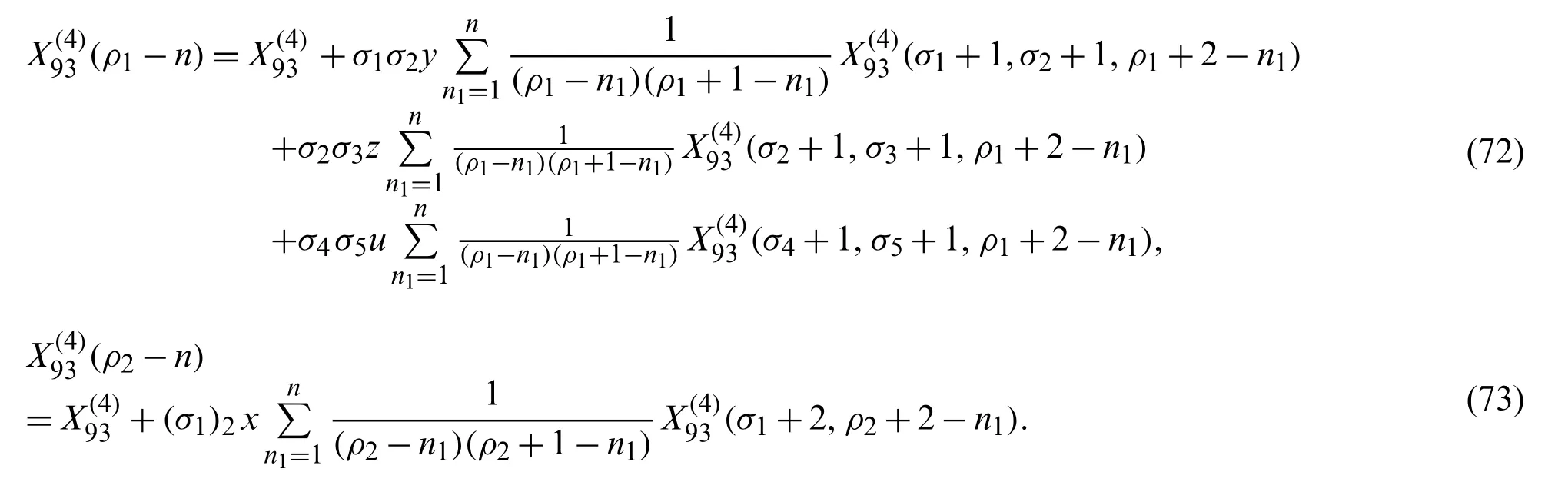
Theorem 2.10The following recursion formulas hold true for the numerator parameterσ1,σ2,σ3,σ4,σ5of the

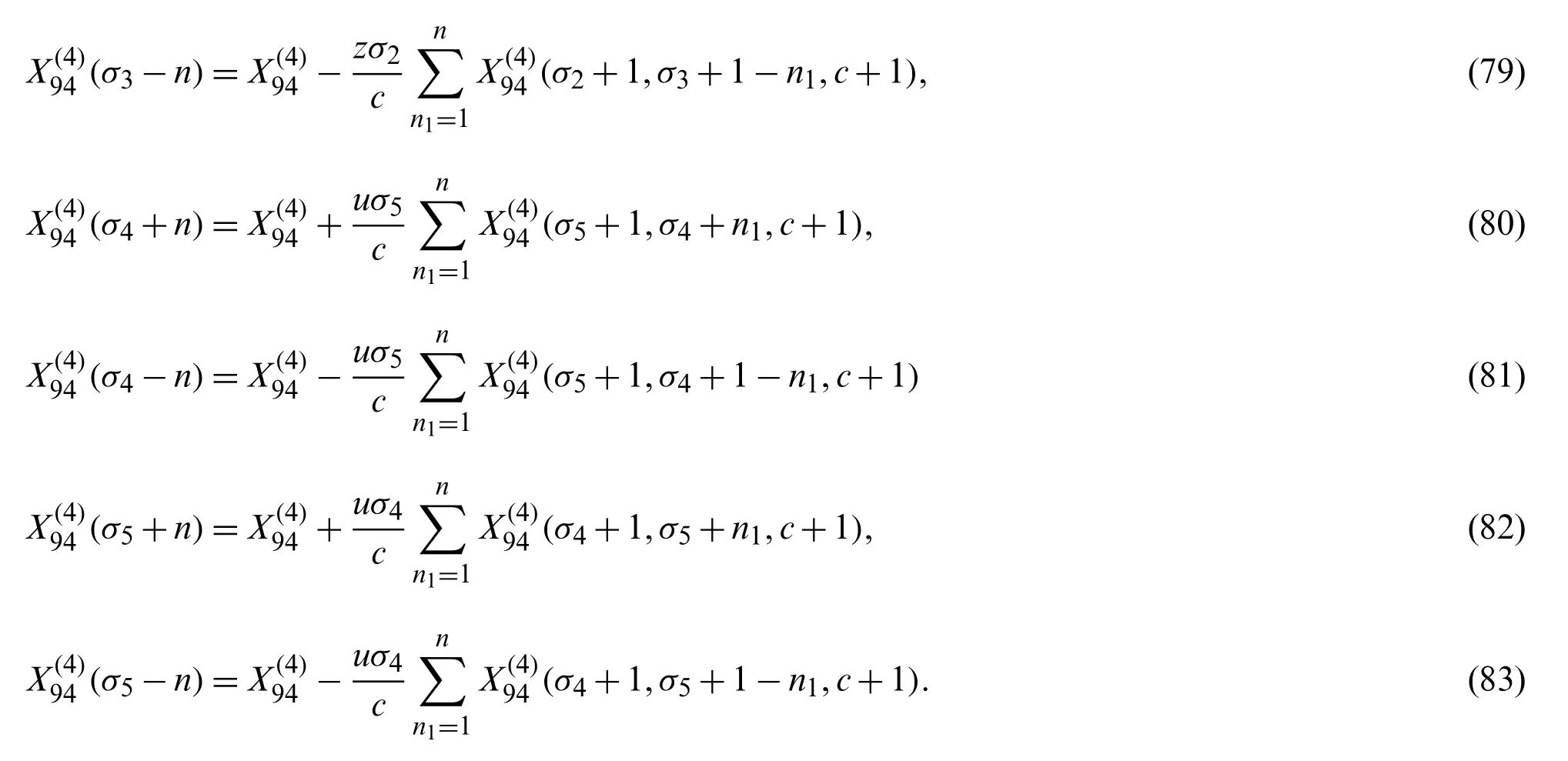
Theorem 2.11The following recursion formulas hold true for the numerator parameterσ2,σ3,σ4,σ5of the

whereN2=n1+n2.

Theorem 2.12The following recursion formulas hold true for the denominator parameter c of the

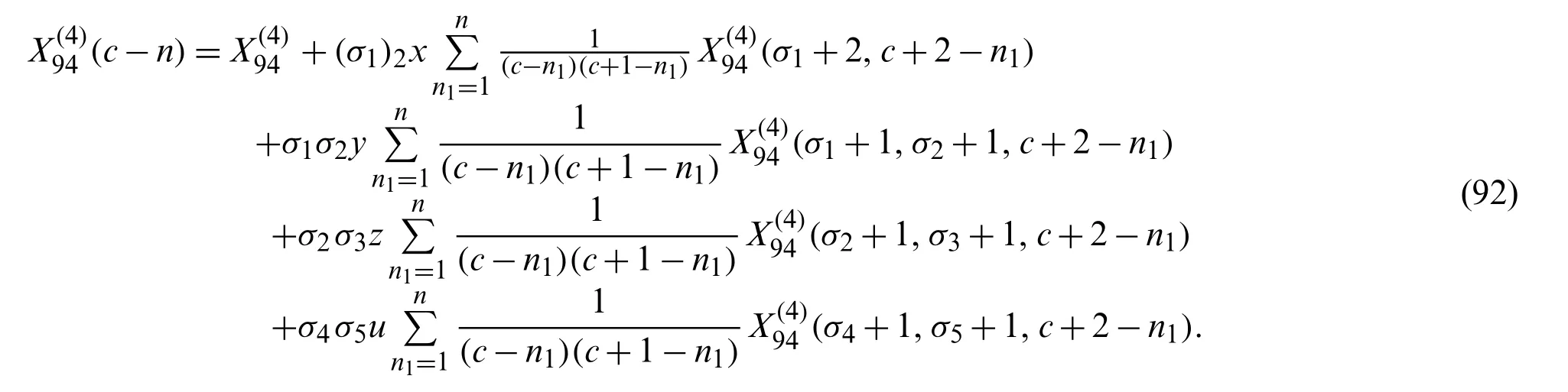
3 Conclusion

Hypergeometric functions in several variables play an essential role in diverse areas of science and engineering.The advancements in applied mathematics,mathematical physics,and other areas of science have led to increasing interest in the study of hypergeometric functions.Also,special functions and its properties are used to solve various problems in science and engineering.In this paper,we have derived several recursion formulas for new hypergeometric functions in four variables.Also,some interested particular cases and consequences of our results have been discussed.In the future,these recursion formulas for the hypergeometric functions in four variables may find applications in various branches of mathematics,mathematical physics,engineering and related areas of study.

Data Availability:The data used to support the findings of this study are available from the corresponding author upon request.

Authors’Contributions:All authors contributed equally and significantly in writing this article.All authors read and approved the final manuscript.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no competing interests.