A Mathematical Model and Simulations of Low Temperature Nitriding

Bogusław Bo˙zek,Lucjan Sapa,★,Katarzyna Tkacz-miech,Marek Danielewski and Janusz Rybak

1AGH University of Science and Technology,Faculty of Applied Mathematics,Cracow,30-059,Poland

2AGH University of Science and Technology,Faculty of Materials Science and Ceramics,Cracow,30-059,Poland

ABSTRACT Low-temperature nitriding of steel or iron can produce an expanded austenite phase,which is a solid solution of a large amount of nitrogen dissolved interstitially in fcc lattice.It is characteristic that the nitogen depth profiles in expanded austenite exhibit plateau-type shapes.Such behavior cannot be considered with a standard analytic solution for diffusion in a semi-infinite solid and a new approach is necessary.We formulate a model of interdiffusion in viscoelastic solid(Maxwell model)during the nitriding process.It combines the mass conservation and Vegard’s rule with the Darken bi-velocity method.The model is formulated in any dimension,i.e.,a mixture is included in Rn,n=1,2,3.For the system in one dimension,n=1,we transform a differential-algebraic system of 5 equations to a differential system of 2 equations only,which is better to study numerically and analytically.Such modification allows the formulation of effective mixed-type boundary conditions.The resulting nonlinear strongly coupled parabolic-elliptic differential initial-boundary Stefan type problem is solved numerically and a series of simulations is made.

KEYWORDS Nitriding; expanded austenite; Maxwell solid; Darken method; Vegard rule

List of symbols

1,2 Components,1 ≡Fe,2 ≡N

ΩiPartial molar volume of the i-th component

Ω Molar volume of the mixture

DiDiffusivity of the i-th component

BiMobility of the i-th component

T Temperature

t Time

R Gas constant

ci(t,x) Concentration of the i-th component

Ni(t,x) Molar ratio of the i-th component

NsL(t) Surface nitrogen concentration at the left boundary

NsL,∞Steady-state nitrogen concentration at the left boundary

yi(t,x) Volume concentration of thei-th component

c(t,x) Overall concentration of the mixture

μi(t,x) Chemical potential of thei-th component

μ°iChemical potential of a reference state of thei-th component

ai(t,x) Activity of thei-th component

fi(t,x) Activity coefficient of thei-th component

θi(t,x) Thermodynamic factor of thei-th component

Ji(t,x) Overall flux of the ith component

Jdi (t,x) Diffusional flux of thei-th component

P(t,x) Local pressure(stress)

v(t,x) Local material velocity(drift velocity)velocity

ηViscosity coefficient,η∗=

EThe Young modulus

νPThe Poisson number

u0The lattice parameter

u(N2)A linear dependence between the lattice parameter and nitrogen content inFe

[Λ1(t),Λ2] Domain in R

Initial and boundary conditions

Y(x) Initial condition for the Fe volume concentration

PL(t) Dirichlet boundary condition for the dynamic pressure atx=Λ1(t)

YL(t) Dirichlet boundary condition for the Fe volume concentration atx=Λ1(t)

βConstant parameter inNs2(t) function

φ(t) Time dependent function used to expressYL(t)

kf,kb,FConstants used in the Chang-Jaffé boundary condition for nitrogen concentration atΛ1(t)

1 Introduction

Nitriding is a thermochemical surface treatment carried out below eutectoid temperature.In the method,a surface of a solid substrate is modified by inserting (diffusion)of nitrogen from the gas atmosphere,which leads to the development of a compound layer and diffusion zone near the substrate surface [1-3].Nitriding has shown the potential to enhance mechanical properties of the surface layer.The compound layer can improve wear and corrosion resistance [4].The diffusion zone,which grows beneath the compound layer,is responsible for the enhancement of fatigue strength.

Depending on a medium providing nitrogen,the nitriding process can be pack,salt-bath,gas,or plasma nitriding.In the pack nitriding,nitrogen-containing organic compounds are used as a nitrogen source.Salt-bath nitriding is carried out in a molten salt bath.In the gas nitriding process,nitrogen is supplied from the gas atmosphere,usually ammonia,NH3.Plasma-discharge technology is a basis for plasma nitriding [5-9].Basically,it is a glow discharge process in a mixture of nitrogen and hydrogen gases.A bias voltage applied to the substrate causes ions to collide with the surface and enhancing the nitriding effect.Plasma nitriding is the most versatile nitriding process and has many advantages over conventional salt-bath and gas nitriding [10-15].

For the last 30 years,it has been reported in many papers that it is possible to nitride stainless steel in such way that a phase of so called expanded austenite is formed,in which nitrogen concentration can reach 38% but remains in solid solution [13,15-30].Expanded austenite,also known as S phase orγNphase,is a metastable supersaturated solid solution of nitrogen (or carbon)in austenite that forms as a case by diffusion [31,32].It provides high hardness and high resistance against wear,corrosion and fatigue,which is a consequence of compressive residual stresses.Such stresses appear due to lattice expansion while the core material constraints the expansion.The composition-induced expansion accommodates elasto-plastically [33-35].It has been also demonstrated that when nitriding is carried out with the use of high-intensity nitrogen plasma pulses the expanded austenite phase can be formed in ARMCOα-iron.The pure iron,initially inαphase,can be transformed into theγaustenite structure,in which expanded austenite is present [36,37].TypicalN-depth profiles in expanded austenite show high value at the surface,an abrupt decrease following a nearly constant plateau and final decrease to a matrix value.Such behavior clearly deviates from the Fickian diffusion and several models have been proposed to predict formation of the expanded austenite.Williamson et al.[38] theorized that if theCratoms are present in the alloy they tend to trap N atoms nearby octahedral sites.When all theCrtraps are occupied,additionalNatoms rapidly diffuse to the edge of theγNlayer.This model has been mathematically formalized by Parascandola et al.[39] basing on the diffusion equation with trapping and detrapping and has been accepted by many authors [19,20,31,32].In several papers [18,21,22],the non-Fickian distribution of nitrogen has been modeled by assuming a presence of composition-dependent internal stress gradient generated by the nitrogen penetration.The stress gradient yields an additional driving force for the diffusion,next to the concentration gradient.

Galdikas et al.[40] considered a simple case,namely the diffusion flux of nitrogenJNbeing proportional to the gradient of chemical potentialμN(cN,T,p),depending on the nitrogen concentrationcN,temperatureT,and pressurep.Moreover they examined a degenerated situation when the pressurepin solids is proportional to internal stresses:p=−σ.In simple words the pressure is the hydrostatic part of the stress tensor,is analogue of the hydrostatic pressure.They neglected the interdiffusion in Fe-N system,consequently a drift was not analyzed and ignore plastic deformation (in our work we consider the Maxwell solid).They had also different,mathematically complicated boundary conditions on the nitrogen concentrationcNgiven by a suitable differential equation.Kücükyildiz et al.[41] modeled the low temperature plasma nitriding,T∈[420°C,445°C],of austenitic stainless steels,i.e.,the reactive diffusion of nitrogen in isotropic elastoplastic material.At such temperature the diffusivities of metals are very low and interdiffusion process is negligible.The one-dimensional model combines the diffusion of nitrogen,DN(cN,T),the elasto-plastic accommodation of the lattice expansion,the solid solution-strengthening by nitrogen and the reactions (trapping of nitrogen by chromium atoms).A very good agreement was foud between the predicted and experimental composition-depth profiles.

A treatment,which takes into account internal stresses,stress relaxation and the resulting convective transport has been developed by Stephenson [42,43].In his works,Stephenson focuses on the solution in an arbitrary binary system but a discussion of binary conditions is lacking.In this research,we use a similar approach as it has been presented by Stephenson in [42,43] and in our earlier paper [44].Namely,we combine the Darken bi-velocity method with the Vegard rule,the Maxwell model of viscoelestic material and the Gibbs-Duhem equation on chemical potentials.We formulate the model in any dimension.In one dimensional case,we equivalently transform such a differential-algebraic system of 5 equations to a differential system of 2 equations only.This modification allows us giving effective mixed type boundary conditions.The open boundary changes with time.Such a nonlinear strongly coupled parabolic-elliptic differential initial-boundary Stefan type problem is solved numerically using the constructed implicit finite difference methods.They are generated by some linearization and spliting ideas.From a numerical and analytical point of view,it is better to study the reduced differential system of 2 equations than the differentialalgebraic system of 5 equations proposed by Stephenson.The interdiffusion during the nitriding is simulated in one dimension and different boundary conditions are discussed.A comparison of our numerical simulations with simulations obtained with the use of some known physically simpler models,for example given in [40],we will present in our future papers.

2 Theory

The overall interdiffusion process can involve a variety of interactions between the diffusive transport,internal stresses,convection (drift)and deformation (plastic strain).Fundamental studies of Larche et al.[45] concerning the stress generated during the interdiffusion and its contribution to a diffusion potential neglect stress relaxation and convective transport due to the plastic deformation.In the Darken method,the potential necessary to drive the plastic deformation is neglected and it is assumed that plastic flow occurs sufficiently rapidly.In such case,the diffusion of a “faster” component is rate-limiting.At relatively small distances,like in the surface layer,the diffusion of “slower” component can become the rate limiting step.When it is true,a simple diffusion equation is not sufficient to describe the overall interdiffusion.A treatment which takes into account both internal stresses,stress relaxation and the resulting convective transport has been developed by Stephenson [42,43].In the present study,we extend this idea and consider interdiffusion vector fluxesJi=Ji(t,x)∈Rn,x∈∑=∑(t)⊂Rn,n=1,2,3,i=1,...,sin thescomponent system given constitutive equations:

whereBi,Ωi,ci=ci(t,x),μi=μi(t,x)are mobility,partial molar volume,concentration of theith specie and its chemical potential.It is assumed thatBiandΩiare constant,i.e.,composition independent.P=P(t,x)is the local pressure andv=v(t,x)is the local material velocity (drift)common for all components [46-48].

The first term in (1)describes chemical diffusion due to the gradient of the chemical potential.The second and third terms represent diffusion due to the non-uniform stress and convective transport,respectively.Convection generates viscous flow and the use of proper constitutive relation is mandatory at low temperatures.A good choice is the Maxwell solid.

Viscoelasticity is a property of materials that exhibits both viscous and elastic characteristics when undergoing deformation.The Maxwell model predicts that when a material is put under stress,the strain has two components:(i)an elastic component occurring instantaneously and corresponding to the spring,which relaxes immediately upon release of the stress; (ii)viscous component that decreases with time as long as the stress is applied which seems accurate for interdiffusion at short distances.

Let us use a simple example of the two-component interdiffusion,s= 2,for example between the solid metallic substrate (Me)and nitrogen (N)from a gas atmosphere.It is assumed that partial molar volumes and the diffusivities of theMe,Ncomponents are constant,i.e.,concentration independent.Consider the following physical equations.

Continuity equations:

The overall fluxJiof the specie in (2)is given by (1).The symbol “·” stands for the standard inner product in Rn.

Vegard rule:

Maxwell solid:

whereη∗=andηis the viscosity coefficient.The Maxwell solid equation determines kinetics of the plastic strain (viscous flow)and combines the convection velocityvwith the pressureP.

The nonideal solute chemical potential is assumed

whereμ°i,ai=ai(Ni),fi=fi(Ni)denote the chemical potential of a reference state,the component activity and the activity coefficient,andNi=Ni(t,x)is a molar ratio of the component,Ni=,c=c1+...+cs,Ris the gas constant andTmeans the temperature.The activity coefficient will be taken a function of hydrostatic pressure,see Part 3.1.Assume thatf2can be expressed by the suitable explicit formula as a function ofN2(see (29))but there is not known an explicit formula onf1.We treatμ2as a known function expressed byN2(or equivalentlyc1,c2)andμ1as an unknown.

We postulate local-equilibrium,isothermal,isobaric conditions which imply

Gibbs-Duhem equation:

or equivalently

It is easy to verify that from (2)and (3)we get

Volume continuity equation:

Our object to study is the differential-algebraic system (2)-(4),(6)of 5 equations with (4 +n)unknowns:c1,c2,v,Pandμ1.It is because ofv∈Rn.Using (1)and (8)this system can be equivalently written in the following form:

Limiting cases of the above system are:

(1)Rapid plastic flow(Darken bi-velocity).

(2)No plastic flow.

Rapid plastic flow.In theDarkenbi-velocity method,it is assumed that the plastic flow occurs rapidly andP= const,∇P= 0.Then the system (9)is simplified to

with the unknownsc1,c2,vandμ1.Consider the casen= 1.By Eq.(5),we have

where the thermodynamic factorIn view of the Gibbs-Duhem Eq.(7),can be expressed as

Hence the volume continuity equation,Eq.(8),takes the form

and in consequence

whereK(t)is an arbitrary function.Assume that the domain∑⊂R is an interval andΩ1J1+Ω2J2= 0 on one boundary of∑.It implies thatK(t)= 0 and the interdiffusion flux is as follows:

Whenf1= 1 (ideal solution)andΩ1=Ω2=Ω=c−1one gets the Darken simple relation

where the diffusivityDi=RTBi,i= 1,2.

No plastic flow.If the material velocity is negligible,v= 0,there is no plastic deformation,and the system (9)is reduced to

with the unknownsc1,c2,Pandμ1.Consider the casen= 1.Reasoning similarly as in the previous situation,for the rapid plastic flow,we get

Elementary calculations lead to the relation for the interdiffusion flux

Ifc= const,then

where

Moreover ifB2≪B1andΩ1=Ω2=Ω=c−1,then (21)simplifies to

and for an ideal solid solution,for whichf1= 1,we obtain

The above means that,whenv= 0 then the slower component is rate limiting.

We will consider in this paper the casen= 1.Ifn≥2,then the number of the equations in (9)(also in Eqs.(2)-(4),(6))and the unknowns is different so the problem is mathematically badly posed.Ifn= 2 orn= 3,∑is a simply connecting region and rotv= 0,then there exists a scalar potentialΦof the driftv,i.e.,

(see [49-51]).The same remarks are true for (10)and (17).Such a situation will be studied in the future.Add that existence,uniqueness and some properties of solutions to one-dimensional interdiffusion model with the drift,but without the chemical potentials and pressure,were proved in [52].

3 Formulation of Practical Model

In this section,we consider a mathematical model of the nitrogen transport during the nitriding in one-dimensional case,n= 1.The model includes the diffusional and convective transport,stress formation and plastic flow.We will transform the system (9)to a system of two equations with the unknownsy1andP.Such a system will be better from a mathematical and numerical point of view.

Theassumptionsare:

1.s= 2,1 ≡Fe,2 ≡N,the binary one-dimensional system in∑=[Λ1(t),Λ2]⊂R,free for nitrogen at the left boundary,x=Λ1(t),while the right boundary,x=Λ2,is a center of the sample.

2.The diffusing components have various diffusivities (D1≠D2)and various partial molar volumes (Ω1≠Ω2),the diffusivities and partial molar volumes are constant,i.e.,composition independent.

3.TemperatureT= 723K.

We introduce new variables

which are interpreted as volume concentrations.It is clear that

because of the Vegard rule.

3.1 Chemical Potential

The chemical potentials of iron and nitrogen are given by (5),where especiallyRTlnf2=−Ω2σh,f2=f2(N2)means the activity coefficient of nitrogen.The hydrostatic stressσh=σh(N2)can be expressed by the compressive residual stress parallel to the surfaceσh=‖.It can be calculated from the lattice dilatation due to the nitrogen penetration,as it results from the Vegard rule

whereEis the Young modulus of Fe (we neglect here a dependence ofEon the nitrogen content and assume the value for pure Fe),νPis the Poisson ratio,u0means the Fe lattice constant andu=u(N2)=u0+u1N2represents a linear dependence of the lattice constant on the nitrogen content.Hence

whereu0,u1,E,νPare known constants.Therefore,the activity coefficientf2can be written as

By Eq.(5),we have

where the thermodynamic factors.In view of the Gibbs-Duhem equation we obtain

Note thatN1+N2= 1,by the definition.Eqs.(30)and (31)imply

It follows from (29),the form ofθ2and Appendix A that

In this way,θ1can be expressed as a function ofy1.

3.2 System of Equations

Taking into account the Maxwell solid equation,the following relation holds

Upon assuming that at the right boundaryv(t,Λ2)= 0,the time-dependant functionK(t)can be calculated

and hence the drift velocity is

In consequence,the first equation in (9)becomes

Combining the volume continuity equation with the Vegard,Maxwell solid and Gibbs-Duhem equations gives

By Eq.(5),we have

where the thermodynamic factorIt follows from Appendix A that:

and Eq.(38)becomes

where

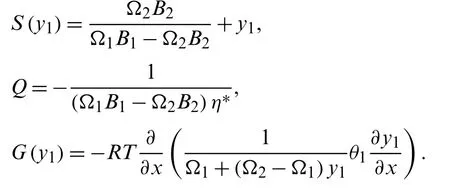
For detailed derivation of (41)see Appendix B.Hence the system (9)can be written in the form

with the unknownsy1andP(see (32),(33)).

Eq.(42)is a parabolic-elliptic system of nonlinear nonlocal strongly coupled differential equations on the domain [Λ1(t),Λ2],whereΛ1(t)is the solution of the initial value problem

that by (36)can be written in the form

For the system (42),we formulate the initial condition att= 0,

whereYis a given function.The boundary conditions will be discussed in the next section of the paper.

3.3 Boundary Conditions

For Eq.(42)we give the following mixed boundary conditions BC.

1.At the right boundary,x=Λ2,the Neumann BC fory1andP,

2.At the left boundary,x=Λ1(t),the Dirichlet BC forP,

wherePLis a given function.

3.Two types of BC fory1are considered at the left boundary,x=Λ1(t):the Dirichlet and the Chang-Jaffé.

(a)The Dirichlet BC

whereYLis a given function.The question is whatYLto propose.For this purpose,the surface nitrogen concentration is given by the function [53],

where=const is a surface-nitrogen concentration att→∞(equilibrium steady-state surface concentration)andβis a constant parameter that tells how fast(t)approaches.For the boundary condition (48)and experimental depth profiles,Christiansen et al.[22] determined,by inverse modeling,theβparameter to be 0.0001.By noting thaty1=Ω1N1(Ω2−(Ω2−Ω1)N1)−1as has been calculated in Appendix A,we get

(b)Instead,because the left boundary is open for the nitrogen flux,it is reasonable to consider the boundary as an interface and assume that there is no accumulation of nitrogen “within” it.In such a case,we can write

wherekf,kb,Fare given constants.Equivalently,it can be expressed in the term ofy1,

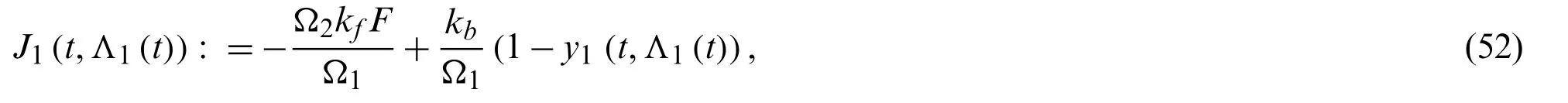
by (26)and Appendix C.In consequence,using (36)and (40),we get

at the points (t,Λ1(t))(see (32),(33)).The above formula is called the non-local Chang-Jaffé BC.

3.4 Data and Results

For the system (37)-(41),the set of data have been applied,Tab.1.Constant diffusivities(mobilities),i.e.,concentration independent,have been used.Most of the computations have been made assuming forFethe highest diffusivity in theαphase (equal to the lowest diffusivity in theγphase)[54].For this diffusivity,a plateau appears at the nitrogen concentration profile,Figs.1-3,5-7,which is according to the expectations.Such a choice agrees with the supposition that the diffusion in the expanded austenite is faster that it is expected from chemical diffusion [18].

Table 1:The data used in the simulations

To study an effect of viscosity on the nitrogen transport,we have made the simulations for the experimentally found viscosity coefficient,2.5 · 103Pa · s (see [61])and repeated them for the two extreme values calculated theoretically for the pureFeandFewith 0.25Nat.%; 1.8 · 104and 1011Pa · s,respectively.In calculations of these extreme viscosity coefficients,the Stokes-Einstein relation,which combines the viscosity with diffusivity has been used.For the binary system it is [43]:

wherec=Ω−1,dis a distance between the atoms,DNPis the Nernst-Planck interdiffusion coefficient andγis a geometric factor,γ≈10.An effect of a sample thickness on the stress distribution and concentration profiles has been also studied and the simulations have been repeated for 4 different sample thicknesses.Besides,the computations for various boundary conditions have been made.

The programming has been performed using the Chesbyshev-Gauss-Lobatto and power grids.In Fig.1,we show that the results don’t depend on the choice of the grid.Therefore,we have arbitrarily decided to perform the remaining computation using the program based on the power grid.

In Fig.2a comparison of simulations made for the two types of boundary conditions for nitrogen concentration at the open boundary is presented.We consider the Dirichlet and Chang-Jaffé boundary conditions.Although in the case of the Chang-Jaffé condition,the nitrogen concentration at the open boundary is calculated in the self-consistent way,without assuming given values,the both curves clearly overlap.The results also show that the concentration profile after 30 min of the processing exhibits an inflection,which at longer times transforms into a plateau characteristic for the non-Fickian diffusion in the expanded austenite.

Figure 2:(a)Time evolution of the nitrogen concentration-depth profiles simulated with the use of the Dirichlet and Chang-Jaffé boundary conditions for the nitrogen concentration at the free left boundary Λ1(t); (b)spatial pressure distribution after 15 h of the processing.The data for the experimental viscosity coefficient

An effect of partial molar volume (here partial molar volume of nitrogen)is presented in Fig.3,where we show the nitrogen concentration and pressure after 15 h of the processing.The assumed values are:Ω2=4.24·10−6m3/mol-according to Jesperson [57] andΩ2= 1.73 ·10−5m3/mol-according to ChemGlobe.It is seen that the variation of theΩ2affects mainly a case depth while the characteristic plateau does not dissappear.This fact confirms the validity of our model.

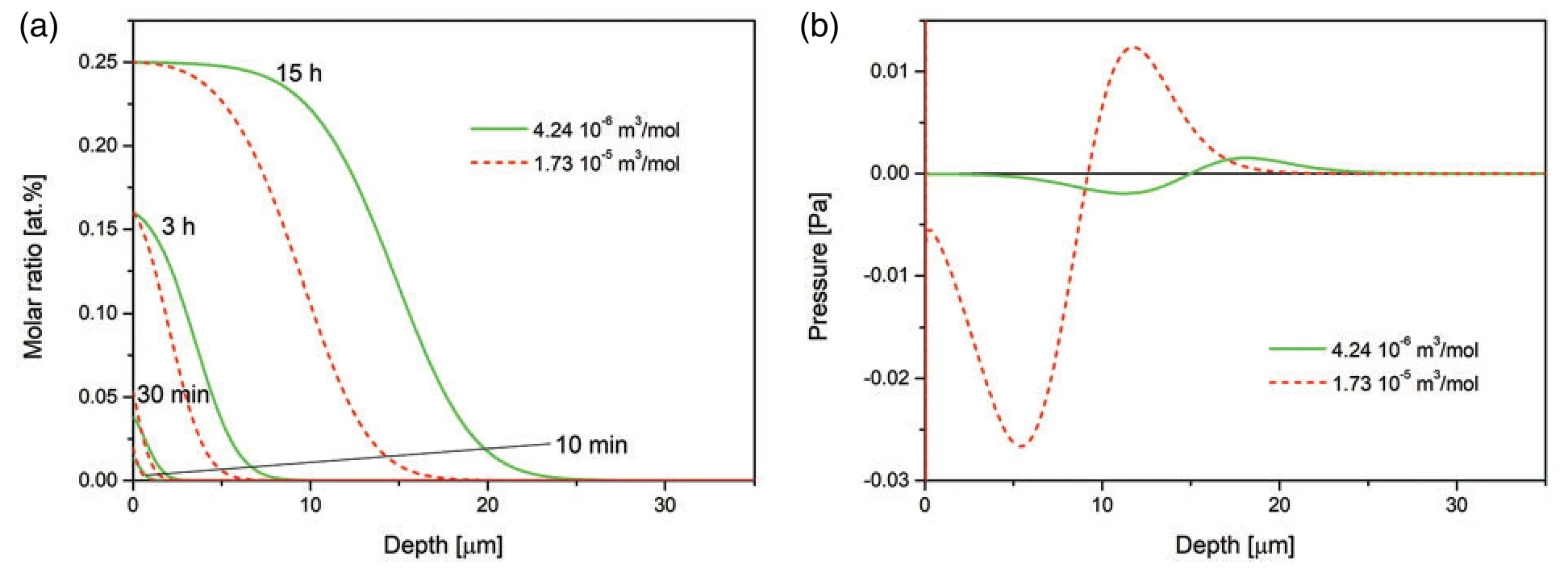
Figure 3:(a)Time evolution of the nitrogen concentration-depth profiles simulated for the nitrogen partial molar volume Ω2 = 4.24 · 10−6 m3/mol given in [57],and the nitrogen partial molar volume Ω2= 1.73 · 10−5 m3/mol given in https://chemglobe.org/ptoe/; (b)spatial pressure distribution after 15 h of the processing.The data simulated for the Dirichlet BC and experimental viscosity coefficient

When we assume theFemobility equal to that at 723 K [54],B1=1.66·10−22mol·s/kg,the results are qualitatively different.The plateau disappears and the sample becomes elongated,Fig.4.Pressure distribution is also qualitatively different.It is because the computational time is too short for such a small mobilityB1.For the plateau to appear,the time would have to be around 1500 h.

Figure 4:Time evolution of the nitrogen concentration-depth profiles (a)and spatial pressure distribution (b),simulated for B1 = 1.66 · 10−22 mol · s/kg (the Fe mobility in 723 K).The profiles after 10,30 min,3 and 15 h of the nitriding.The data simulated for the Dirichlet BC and experimental viscosity coefficient

In Fig.5,the results for 4 samples of different thicknesses are presented.It is seen that the amount of the nitrogen dissolved and the case depth decrease when the layer thickness increases,Figs.5e-5f.The observed differences are due to various stress distribution in the samples of various thicknesses.The pressure changing with the depth (pressure gradient)implies an additional driving force for the diffusion.It is seen that the pressure gradient decreases at longer times.

Figure 5:(a-d)Time evolution of the nitrogen concentration together with the spatial pressure distribution (in insets)simulated for the samples of various thicknesses,the respective profiles after 10,30 min,3 and 15 h of the nitriding; (e)comparison of nitrogen concentration profiles after 15 h of the nitriding of the samples of various thicknesses; (f)amount of nitrogen dissolved in the samples vs. time.The data simulated for the Dirichlet BC and experimental viscosity coefficient

Only quantitative differences are seen when the final nitrogen concentration at the open boundary is increased from 0.25 at.% to 0.35 at.%,Fig.6.

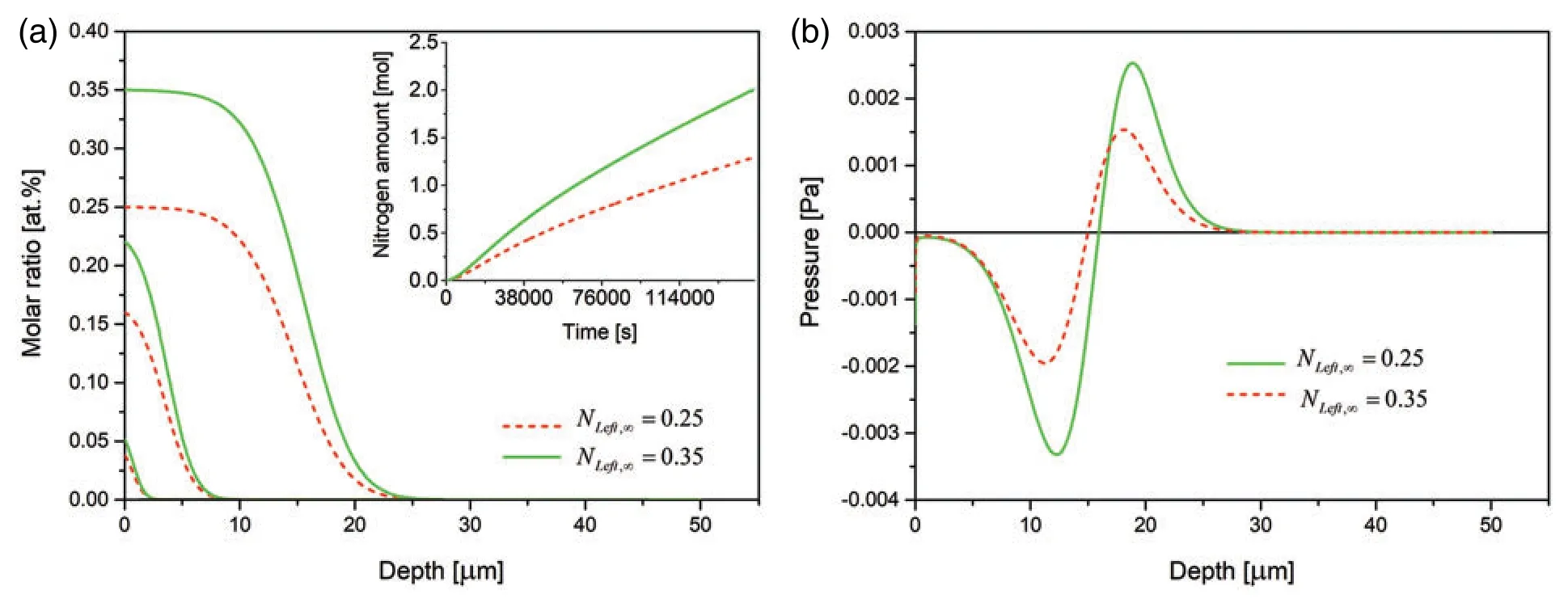
Figure 6:(a)Time evolution of the nitrogen concentration together with nitrogen dissolved (in inset)and (b)spatial pressure distribution for various steady-state nitrogen concentrations at the free left boundary Λ1(t),0.25 and 0.35 at.%.The respective profiles after 30 min,3 and 15 h of the nitriding.The data simulated for the Dirichlet BC and experimental viscosity coefficient

The effect of viscosity coefficient is presented in Fig.7.It is seen that with increasing viscosity coefficient the case depth decreases and less nitrogen is dissolved in the substrate.

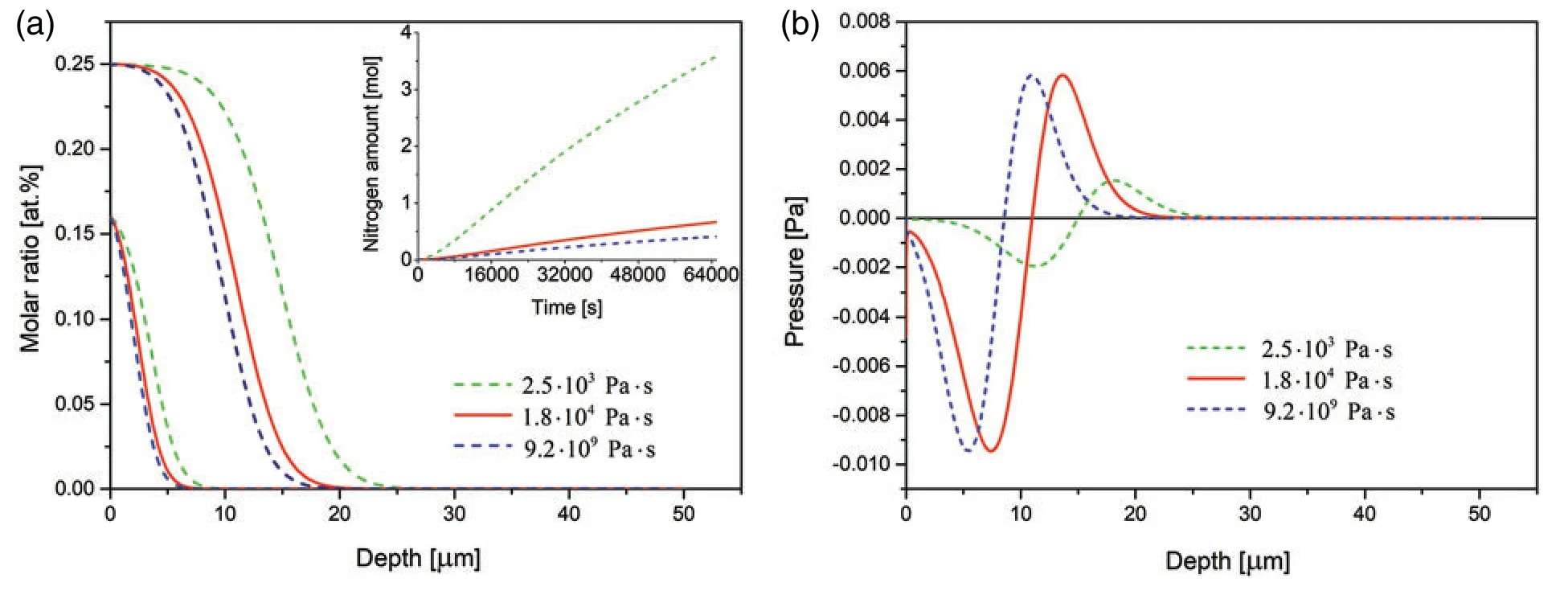
Figure 7:(a)Time evolution of the nitrogen concentration together with nitrogen dissolved (in inset)and (b)spatial pressure distribution simulated for the 3 samples of various viscosity coefficients.The respective profiles after 3 and 15 h of the nitriding.The data simulated for the Dirichlet BC

The presented results show that the appearance of the plateau at the nitrogen concentration profiles is conditioned by the mobilities of the species.It appears when the Fe mobility is higher than that at 723 K.Such processing can be realized in plasma conditions.The sample elongation is not observed.Qualitatively different results are obtained when assuming Fe mobility at 723 K (about 5 orders lower).No plateau appears and the sample becomes elongated.The characteristic plateau-type shape of theN-concentration depth profile has been confirmed by many authors [4,21,28].Christiansen et al.in [20-22,28] studied the effects of in-depth stress gradients in expanded austenite.The obtained profiles showed a clear plateau followed by a steep nitrogen concentration decrease.Our results agree well with these results.Also,the experimental data measured by electron probe microanalysis (EPMA)in AISI 316 steel after low-temperature nitriding (440°C)for 23 hours at the nitriding potentialKN=1.41bar−1/2(at which the surface nitrogen concentration is 0.25 at.%)and presented in [22] (Fig.4)show the validity of the calculated profiles.By comparing the thickness of the nitride zone,our simulation provides an overestimate.The validity can be improved by adopting concentration-dependent diffusivity.

4 Summary and Conclusions

Low and intermediate-temperature nitriding of iron and stainless steel can cause a formation of expanded austenite phase.In this research,a formation of expanded austenite is modeled using the Darkenbi-velocity method combined with the Vegard rule,the Maxwell model of viscoelastic solid,and the Gibbs-Duhem equation.It is the first such approach,which takes into account the interdiffusion of all components in the solid alloy.The model is formulated in any dimension and is given by a differential-algebraic system of 5 equations.In the one dimensional case,this system is equivalently transformed to the differential system of 2 equations only,which from analytical point of view is better to be studied.Effective mixed type boundary conditions are given.Such a nonlinear strongly coupled parabolic-elliptic differential initial-boundary Stefan type problem is solved numerically.A series of simulations is made.The results confirm an appearance of the characteristic plateau on the nitrogen concentration-depth profiles which is in agreement with literature data (see for example [20-22,28]).The model can be improved by the way of using concentration dependent diffusivities.It can be concluded that:

• The nitrogen transport during nitriding is advanced by means of the stress and strain assisted interdiffusion.

• The stress enhances the diffusion.

• The interdiffusion can cause an imbalance in the volume transport and a non-uniform stress-free strain.

• The stress and strain depend on the components’ mobilities,viscosity coefficient and thickness of the substrate.

• Relaxation of the internal stresses generated by unbalanced diffusion fluxes can become the rate-limiting step for the interdiffusion.

The Maxwell model is usually applied to the case of small deformations.For the large deformations one should include non-linearity,e.g.,the upper-convected Maxwell model.It can be further improved by the way of using concentration dependent diffusivities.

The initial boundary value problem presented here can be extended and even used in practical applications.

Appendix A

To express the chemical potential gradientas a function ofy1,let us notice first thatN1=,y1=Ω1c1,Ω1c1+Ω2c2= 1 andc1+c2=c.We can write:

After introducing (56)and (57)into (39)leads to (40).

Appendix B

We want to find a differential equation on the pressureP.The formulas (38)and (40)imply the relation

It follows from elementary calculations that

By inserting (59)to (58)we have

and equivalently

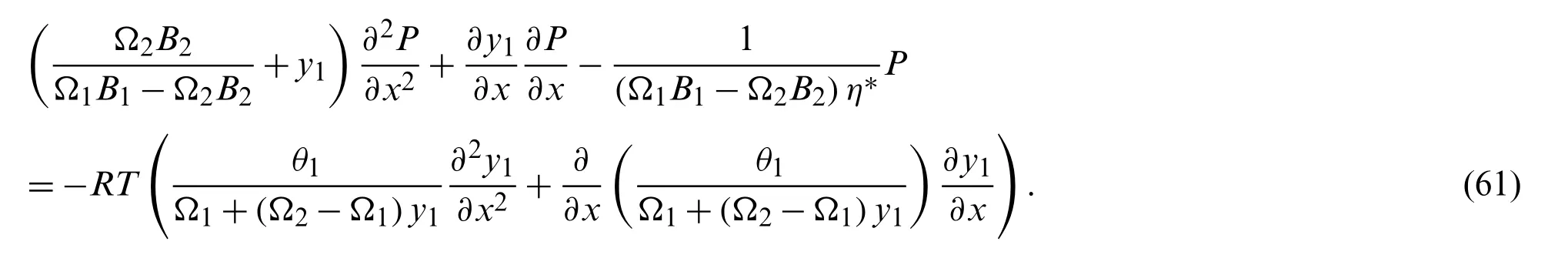
In fact Eq.(61)is identical with Eq.(41).

Appendix C

We will show that

It follows from (8)that

by one dimensionn= 1.Letmean the diffusion terms of the fluxesJi,i= 1,2 given in (1).Because at the right boundaryv(t,Λ2)= 0 andthenK(t)≡0 and in consequence (62)is satisfied.

Appendix D

We will construct implicit finite difference methods for the system (42)with the initial condition (45)and two types of boundary conditions:(46)-(48)-the Robin type,and (46),(47),(53)-the generalized non-local Robin type,respectively.These numerical methods are generated by some linearization and spliting ideas.The date used in simulations are given in Table 1.To avoid a double indexation,we put:y:=y1andθ:=θ1.

Define a mesh on the set [0,∞)×∑(t)= [Λ1(t),Λ2] in the following way.Letτ >0 stands for the time step of the mesh and define nodal time pointstν=ντ,ν∈N ∪{0}.Let moreoverM∈N be given,be at this moment arbitrarily fixed nodal space points and letm=1,...,M+1 mean the space steps of the mesh.Define new nodal space points,m=0,...,M.Note thatPut

For the left end of the domain∑(t),the approximation of (44)is applied,

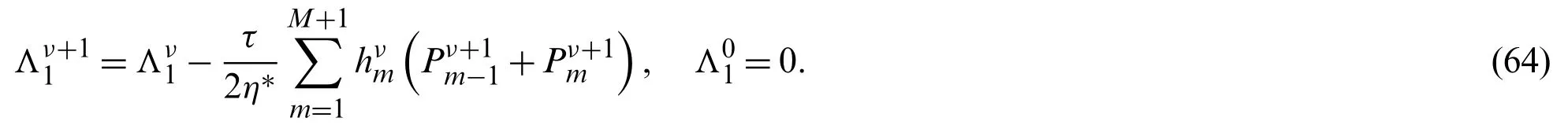
Two definitions on the space nodal points will be used in computations:

fors= 3/2 ors= 2;

Eq.(65)describes the power and Eq.(66),the Czebyshev-Gauss-Lobatto grids.

We define two linear implicit difference schemes:for the ordinary equation on pressurePand for the parabolic equation on concentrationy1in system (42)with the initial-boundary conditions(45)-(48).For eachν,they are algebraical systems ofM+1 equations withM+1 unknowns of the form

where

If we consider a finite difference method for system (42)with the initial-boundary conditions(45)-(47),(53),then a discretization of (53)is as follows:

Funding Statement:This work has been supported by the National Science Center (Poland)Decision No.UMO-2013/11/B/ST8/03758 and by the Faculty of Applied Mathematics AGH UST statutory tasks within subsidy of Ministry of Science and Higher Education (Grant No.16.16.420.054).Research data are referenced in Section 3.4.They will be available on requirements.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.