Theoretical Investigation of Two-Dimensional Nonlinear Radiative Thermionics in Nano-MHD for Solar Insolation:A Semi-Empirical Approach

Usman Inayat,Shaukat Iqbal and Tareq Manzoor

1School of Systems and Technology,University of Management and Technology,Lahore,54000,Pakistan

2Energy Research Centre,COMSATS University Islamabad,Lahore Campus,Lahore,54000,Pakistan

ABSTRACT In this contemporary study,theoritical investigation of nanofluidic model is thought-out.Two-dimensional nanomaterials based mixed flow is considered here.Convective solar radiative heat transport properties have been investigated over a nonlinearly stretched wall in the presence of magneto-hydrodynamic (MHD),by innovative application of semi analytical “optimal homotopy asymptotic method (OHAM)”.OHAM does not require any discretization,linearization and small parameter assumption.OHAM describes extremely precise 1st/2nd order solutions without the need of computing further higher order terms,therefore,fast convergence is observed.Nanofluidic governing model is transformed into system of ordinary differential equations(ODEs)by exploitation of similarity transformation.Tostudy the significance of radiation parameter along with thermophoresis parameter,a semi analytical solver is applied to the transformed system.In this work,Brownian motion,influence of magnetic field,Lewis number,Prandtl number,Eckert number and Biot number have investigated on velocity,temperature and nanoparticle concentration profiles.The study provides sufficient number of graphical representations to demonstrate the inspiration of mentioned parameters.

KEYWORDS Magneto-hydrodynamic (MHD); OHAM; nanofluid; solar radiative; stretched wall

1 Introduction

The most abundance renewable energy source for best alternative to conventional fossil fuelbased generation is solar energy.Electric energy and heat energy can be generated through sun light using photoelectric effect on photovoltaic panels and photothermal conversion on concentrated solar thermal plants,respectively.The increasing rate of solar absorption helps in improving energy output production of both photovoltaic panels and concentrated solar thermal plants.The efficient absorption of solar energy results in reliable use of renewable energy and better conversion into thermal energy,which results in least dependence on fossil fuels.However,the current heat collectors and photovoltaic panels suffer from inefficient sunlight absorption that results in signification energy loss and low efficiency.In this regard,water dispersed nanoparticles are being extensively studied for improving sunlight absorption.Various nanomaterials have been proposed and tested for ameliorating sunlight absorption efficiency.The sunlight absorption capability is improved by using photoactive nanomaterials for polymeric photovoltaic panels.It is known that these polymeric photovoltaic panels absorb photons with bandgap of 2-ev.Therefore,nanomaterials are needed to widen this energy bandgap for absorbing more sunlight.In this regard,a hybrid solar cell was proposed for more solar energy absorption from visible to near-infrared energy band.

The heterojunction photovoltaic cells were examined for analyzing their solar absorption enhancement capability using half-coaxial crystalline silicon nanowire arrays [1].High bandgap solar cell was integrated with upconverter at its for stronger sunlight absorption in the near infrared region [2].The broadband absorption enhancement was achieved in Si films by their crystallization in liquid phase on textured glass.The absorption enhancement was increased by 36.3% as compared to planar reference film [3].A two-dimensional photonic-structured perovskite photovoltaic cell was investigated,which provided 65.7% more absorption efficiency over the visible range [4].Photonic crystals were placed on the top surface of microcrystalline silicon solar cells to enhance light absorption with the exploitation of resonant effects in photonic crystal.The efficiency was reported to be increased by 11% due to enhanced short circuit current density [5].The dye-sensitized photovoltaic cells were combined with uncapped lead sulfide nanocrystals to achieve increase in absorption capability by 7.9% [6].

The index-guiding microstructured optical fiber,which is ionic-liquid adorned,were adopted to construct an optical fiber light detector by splicing it with two air holes in innermost layer.It was reported to have power density sensitivity to achieve value of 1.529 dB/(mW.mm2)[7].The titanium nitride nanoparticles were investigated in water with experimental results to report higher sunlight absorption efficiency as compared to carbon nanoparticles [8].The surface mounted gold particles based copper-dopedTiO2nanocomposites were synthesized using a facile step method.It was observed that they were able to enhance more visible light spectrum absorption as compared to pureTiO2and copper-dopedTiO2[9].The light energy concertation was achieved at mesoscale volumes using light-absorbing nanoparticles contained aqueous solutions.The high efficiency steam was obtained using sunlight even in case of having far below boiling temperature of the bulk fluid [10].The experimental results were presented to show that the rapid water vaporization with sunlight can be achieved using silicon nanoparticles in water [11].Rapid sunlight to heat conversion was achieved using plasmonic nanocomposites with filler concentration at volumetric ppm level [12].Collocation and optimal homotopy asymptotic methods had been used for investigation of third grade non-Newtonian blood fluid [13].Similarly,third grade non-Newtonian blood flow had also been investigated by solving their partial differential equations using differential quadrature method [14].The performance of optimal homotopy asymptotic method (OHAM)found better as compared to fourth order Runge-Kutta numerical method,while investigating micropolar fluid [15].OHAM had also been used for computational analysis of micropolar fluid flow [16].The heat transfer analysis of solar collectors had been performed using OHAM and homotopy perturbation method [17].Peristaltic nanofluid flow had been analyzed using differential tranformation method to study the impacts of Brownian and thermophoresis motions on its flow for drug delivery applications [18].The fourth order Runge-Kutta numerical method with shooting technique had been adopted for solving the governing equations of nanofluid towards a stretching sheet [19].The solar energy induced stagnation-point fluid flow was investigated using Rooseland approximation and shooting technique-based fourth-fifth order Runge-Kutta method.It was reported that the liquid absorbed higher solar radiations due to excessive mobility of nanoparticles [20].The numerical study magneto-hydrodynamic (MHD)nanofluid flow was performed to analyze the effect of solar energy on fluid flow using Keller-Box numerical approach [21].The summary of existing solution methods and fluid types for different applications has been presented in Table 1.Besides these,the dynamics of nanofluidic problems have also been discussed in the literature for different application fields.

Table 1:Overview of existing solution methods and fluid types for different applications

This conducted research explored nanofludics systems numerically and graphically.The less research has been performed on the application of the two-dimensional non-linear radiative heat transfer in the nanofluid flow.The major contributions of the proposed work are:

• Optimal homotopy asymptotic method has been proposed for the numerical solutions of two-dimensional non-linear radiative heat transfer in the nanofluid.

• The performance of OHAM method has been analyzed in terms of convergence rate and the results prove its faster convergence.

• The dynamics of the nanofluid have also been analyzed in respect of Velocity,Nanoparticle concentration profiles,and Temperature profiles studied with the effect of Magnetic parameter,Radiation parameter,Lewis number,Eckert number,Biot number,Prandtl number,Thermophoresis parameter,and Brownian motion.

Rest of the paper is organized as follows:Section 2 presents modeling of nanofluid flow over a stretched sheet,Section 3 discusses optimal homotopy asymptotic method for the numerical solutions,Section 4 provides solution and results to show effectiveness of the proposed method,and Section 5 concludes the proposed research.

2 Modeling of Two-Dimensional Nonlinear Radiative Thermionics in Nano-MHD

Suppose the flow of nanofluid over stretched sheet shown in Fig.1,with convective heating at y=0.Along x-direction the stretching velocity isμω=αx.B0is the magnetic field perpendicular to the flow.μ∞(x)=βxis the free stream velocity.The analysis of heat transfer is done under the influence of viscous dissipation,Joule heating and thermal radiations,with the combined effect of thermophoresis and Brownian motion.

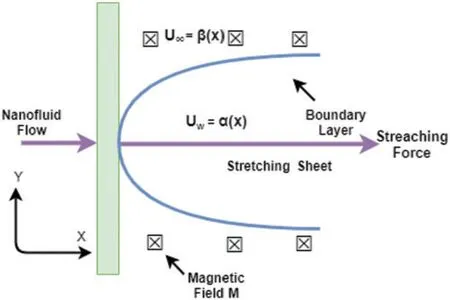
Figure 1:Coordinate system for the physical stretched sheet model

The governing equations of the heat flow under typical boundry conditions can be expressed as [22,23]:

In above Eqs.(1)-(4)velocity component along x-axis isμand along y-axis isυ.KBis the Brownian parameter,KTis the thermophoretic diffusion parameter.ζis the base fluid thermal diffusivity,χfis the density of base fluid,heat capacities are denoted by (χC)fand (χC)p,mrrepresents parameter of radioactive heat flux and nanoparticale concentration is represented byC,where,

In Eq.(5),σdenotes the Stefan-Boltzman constant,n*represents the mean absorption coefficient.Eqs.(2)-(4)can be transformed to:

The boundary conditions will be of the form:

OHAM is used to solve Eqs.(6)-(8)under given boundary conditions.

3 Numerical Method

3.1 Formulation of OHAM

The idea of optimal homotopy asymptotic method (OHAM)is discussed in [24-29].Governing differential equation is written as:

B(u)=L(u)+S(u)whereLis a linear component andSis the nonlinear component.It is worth noting that we have a great freedom to choose theLpart from the model,therefore it does not need to get the first solution (initial guess).κis independent variable,Ωis domain,u(κ)is unknown function,w(κ)is a known function.SubstitutingB(u)in (9),

by applying OHAM on (11):

whereq∈[0,1] is an embedding parameter,nonzero auxiliary functionH(q)atq≠ 0 withH(0)= 0,Φ(κ,q)is an unknown function.Forq=0,1

With the change in value ofPfrom 0 to 1,Φ(κ,q)varies fromu0(κ)tou(κ).Puttingq=0 in (12):

Auxiliary function will be of the form:

whereC1,C2,C3,...are con stants to be evaluated.By applying Taylor’s series with respect toqfor expansion we get:

Comparing (16)and (12),we get following coefficients

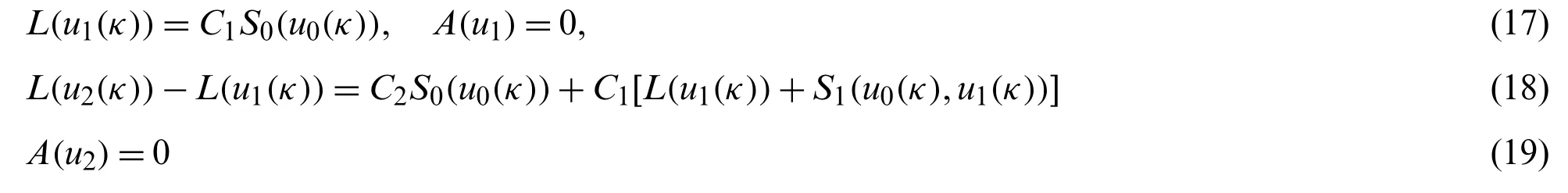
whereSn-i(u0(κ),u1(κ),...,un-i(κ))is the coefficient ofqn-i.expansion ofS(Φ(κ;q))gives that

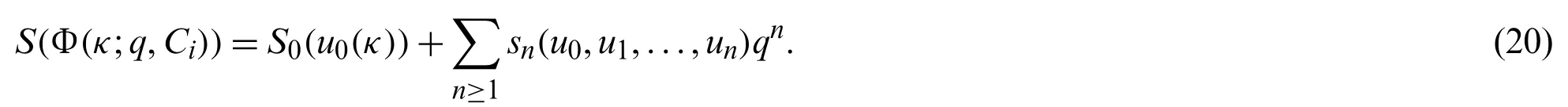
Convergence of the Eq.(16)depends on the values of auxiliary constantsC1,C2,C3,C4...Forq=1

From (21)and (11),we get the residual expansion

We will get exact solution ofú(κ;Ci)ifR(κ;Ci)= 0,it is not always true for nonlinear systems.For the determinations of auxiliary constantsC1,C2,C3,...,following methods can be used:

• Galerkin’s Method,

• Ritz Method,

• Least Squares Method and

• Collocation Method

To find the optimal values of auxiliary constants.Method of least square is the most common method to optimize the errors by taking the square of the residuals over the given domain to get the following functional:

wherex1andx2are the values depending on the given system.The optimal values ofC1,C2,C3,...can be evaluated with minimum error from:

Solving the above system of algebraic equations obtained in Eq.(24),we get the values ofC1,C2,C3,....Replacing the values ofC1,C2,C3,...Ciin Eq.(10),we get the approximate solution.Fig.2 explains the process of modeling and solution of MHD problem using OHAM.

3.2 Validation of OHAM

Validation of the OHAM technique is an essential part of a theoretical study.The aim of validation is to ensure the computations are reliable.For this purpose,we considered singular initial value Lane-Emden [30] model to evaluate our semi-empirical technique.Indeed,OHAM is known for its easy implementation,effectiveness for solving singular phenomena,and producing efficient results with minimum computations.The general representation of Lane-Emden equation is given as follows:

with initial conditions

v(0)=γ,v′(0)=δ.

wheref(v)is a real valued continuous function,γ,δandnare constants.The most common form off(v)=vλ,hereλis tropic index.From literature it observed that the solutions of the Lane-Emden equation could be given in closed form if tropic index is 0≤λ≤5.Forλ= 3,n=2 andg(x)=x5+30,Eq.(25)will become:

with boundary conditionsv(0)= 0 andv′(0)= 0.The exact solution of the Eq.(26)isv(x)=x5[31].

Figure 2:Schematic representation for the MHD flow analysis of nanofluid over a non-linear stretching sheet

Forλ= 1,n=2 andg(x)=x6+6,Eq.(25)will become:

having boundary conditionsv(0)= 0 andv′(0)= 0.The exact solution of the Eq.(27)isv(x)=x2[31].

By applying OHAM scheme Eqs.(12)-(24)subject to the given boundary conditions to evaluate solutions denoted byvOHAM.As shown in Table 2,the effectiveness of OHAM is validated using absolute errors |vExact−vOHAM|,for Eqs.(26)and (27).Table 2 verifies that accuracy is achieved even with the second order approximations.

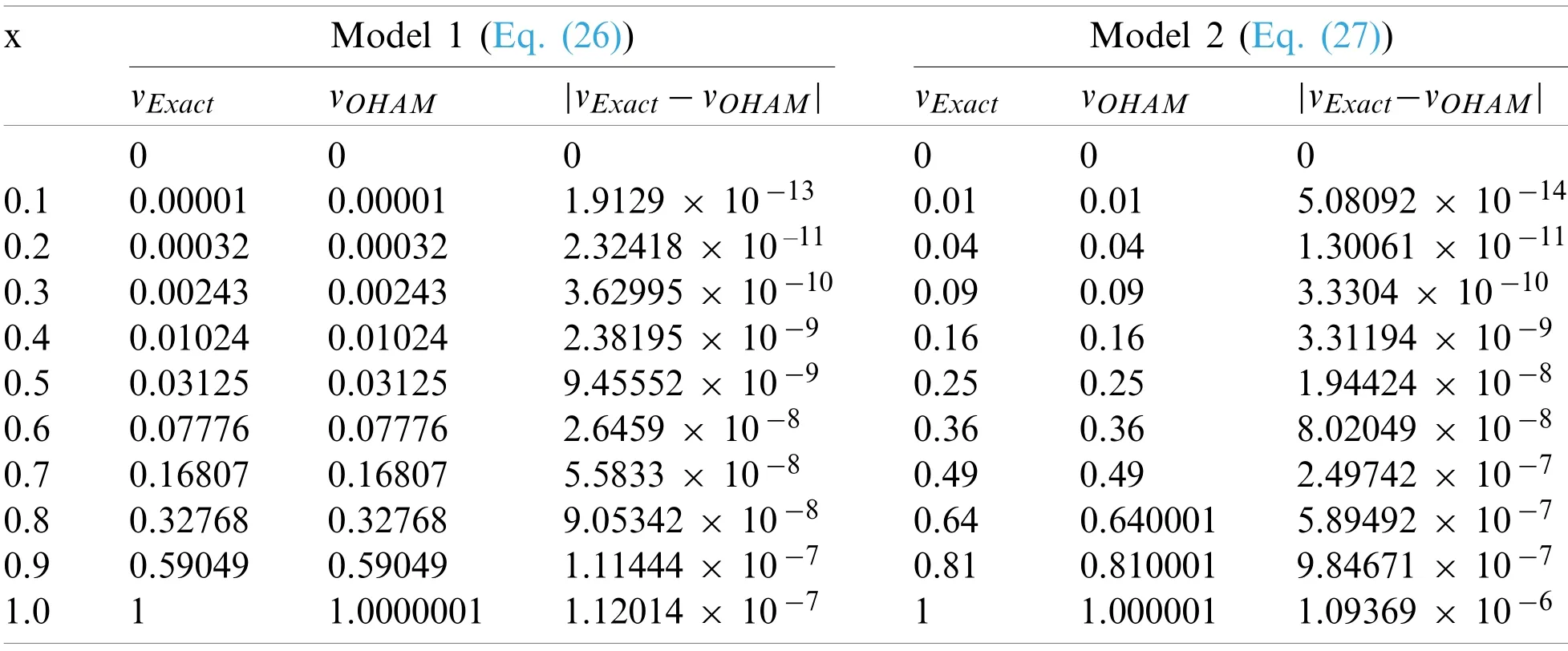
Table 2:Validation of OHAM using absolute errors comparison for Lane-Emden model

4 Solutions and Results

In this section,OHAM is applied to nonlinear ODE’s Eqs.(6)-(8).The homotopy of Eq.(6)is constructed as:

We considerg(η)as follows:

By solving Eqs.(28)and (29),after simplification and equating like powers ofq-terms,we get

The homotopy of Eq.(7)is constructed as:

We considerφ(η)as follows:

By solving Eqs.(33)and (34),after simplification and equating like powers ofq-terms,we get

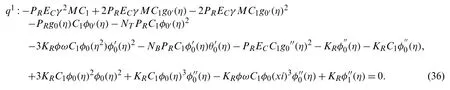
The homotopy of Eq.(8)is constructed as:

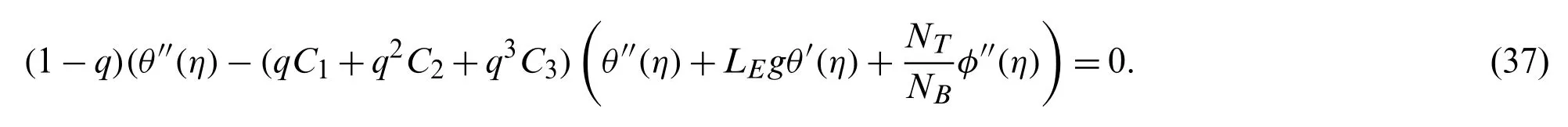
We considerθ(η)as follows:

By solving Eqs.(37)and (38),after simplification and equating like powers ofq-terms,we get

The modified equations obtained from OHAM have been solved using boundary conditions which are provided in Section 2.For solar application analysis of OHAM,solar radiation’s impact in a magnetic field conducted over an extended plate with a nanofluid limit layer has been investigated to illustrate the impact of radiation parameter Velocity profileg(η)with the magnetic parameter M andγwhich is ratio betweenμ∞(x)andμw(x).Influence on local Nusselt numberφ′(η)and temperature profileφ(η)are also analyzed by varying Eckert NumberEc,magnetic field parameterM,radiation parameterKr,Brownian motion parameterNB,Biot numberλ,Prandtl numberPR,thermophoresis parameterNT,and Lewis numberLE.Quantitative illustration of the results for local Nusselt number and local Sherwood number for different physical quantities is provided,in Table 3.The Sherwood numberθ′(η)and nanoparticle concentration Profileθ(η)are also analyzed graphically as presented below.

Table 3:Local Nusslet and local Sherwood numbers for λ= 0.5, γ = 0.5, Pr=2, LE, Ec=0.1 and θw=1

Velocity profile has been presented in Fig.3 in accordance with diverse values of the magnetic parameterMwithγwhich is ratio betweenμ∞(x)andμw(x).The magnetic parameterMcauses the velocity profile to decrease.Fig.4 illustrates the diverse values ofγwith fixed value of the magnetic parameter on velocity profile.It is observed with the increase in value ofγ,g′(η)increases.

Figure 3:Velocity profile g′(η)for different choices of M at γ = 0.5

The impact of radiation parameterKris depicted in Fig.5.Krimpact on temperature profileφ(η)is studied in detail.It is observed that increase inKr,first increases the temperature profileφ(η),followed by a decrease,and lastly,an increase is illustrated.Fig.6 shows the Nusselt Numberφ′(η)for diverse variations of radiation parameterKr.It is observed that increase inKr,first decreases theφ′(η),followed by an increase,and lastly,a decrease is noted.Illustration of the influence of Prandtl numberPRonto the dependent variable temperature profileφ(η)is presented in Fig.7.Decreasing trend is observed inφ(η)with the increase inPR.Effect of Prandtl NumberPRis studied on Nusselt numberφ′(η)in Fig.8.Increment in thePRmakesφ′(η)to increase and decrement ofPRcausesφ′(η)to decrease.Hence,an increasing trend is comprehended byφ′(η).

Figure 4:Velocity profile g′(η)for different choices of γ at M=1

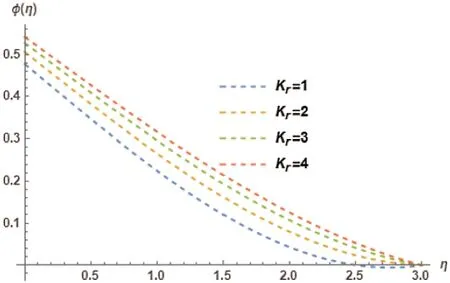
Figure 5:Temperature profile φ(η)for different choices of radiation parameter Kr at M=1, γ =0.5, λ= 0.4, PR=3, NB=0.1, NT=0.1, LE=2, Ec=0.2, φw=1 showing their exciting nature

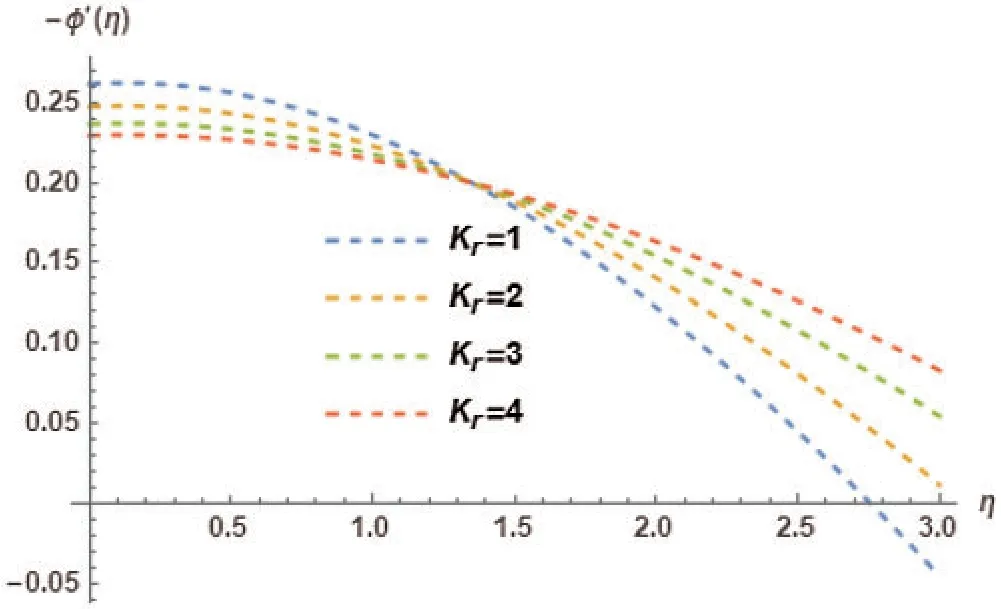
Figure 6:Nusselt number −φ′(η)for different choices of radiation parameter Kr at M=1, γ =0.5, λ= 0.4, PR=3, NB=0.1, NT=0.1, LE=2, Ec=0.2, φw=1 showing their exciting nature

Figure 7:Temperature profile φ(η)for different choices of Prandtl number PR at M=0.5, γ = 0.5,λ= 0.5, Kr=2, NB=0.1, NT=0.1, LE=1, Ec=0.2, φw=1 showing their exciting nature

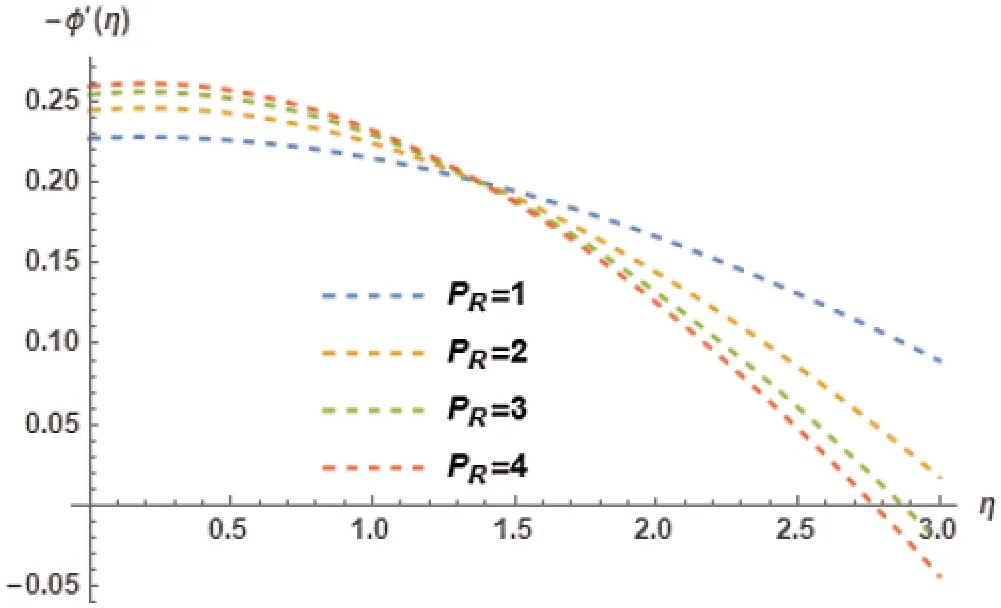
Figure 8:Nusselt number −φ′(η)for different choices of Prandtl number PR at M=0.5, γ = 0.5,λ= 0.5, Kr=2, NB=0.1, NT=0.1, LE=1, Ec=0.2, φw=1 showing their exciting nature

Influence on temperature profileφ(η)in accordance with Thermophoresis parameterNTis discussed in Fig 9.The behavioral pattern comprehends it as an increasing trend.Fig.10 shows the variation ofNTon the local nusselt numberφ′(η).This figure elucidatesφ′(η)with a decreasing trend in accordance with the variation ofNT.Brownian motion parameterNBinfluences on temperature profileφ(η)is shown in Fig.11.The Brownian motion in nanofluids exists due to their size and because of this size the effect of its minisicule particles play an important role in transfer of heat.The basis of definition of Brownian motion; hint towards the kinetic energy of nanoparticles increasing the values ofφ(η)due to the chaotic motion intensity.Hence,an increasing trend is comprehended inφ(η).Brownian motion parameterNBand its association with local Nusselt number is illustrated in Fig.12.A decreasing trend has been comprehended byφ′(η)with the increase ofNT.

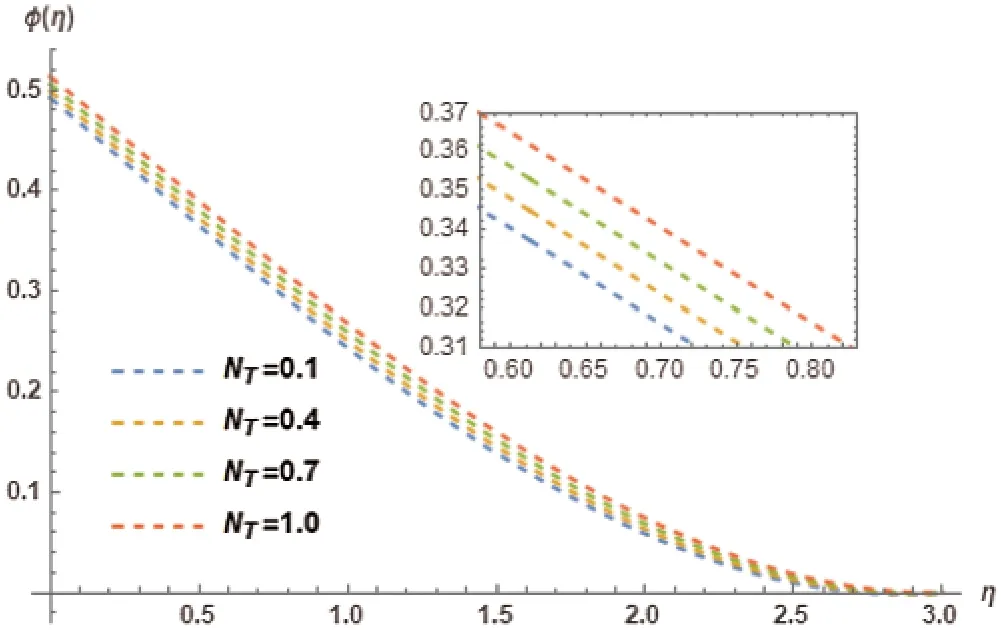
Figure 9:Influence of NT on φ(η)at M=0.5, γ = 0.5, λ= 0.5, PR=4, Kr=2, NB=0.1, LE=1,Ec=0.2, φw=1

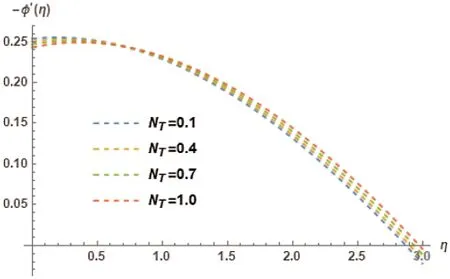
Figure 10:Variation of NT on −φ′(η)at M=0.5, γ = 0.5, λ = 0.5, PR=4, Kr=2, NB=0.1,LE=1, Ec=0.2, φw=1

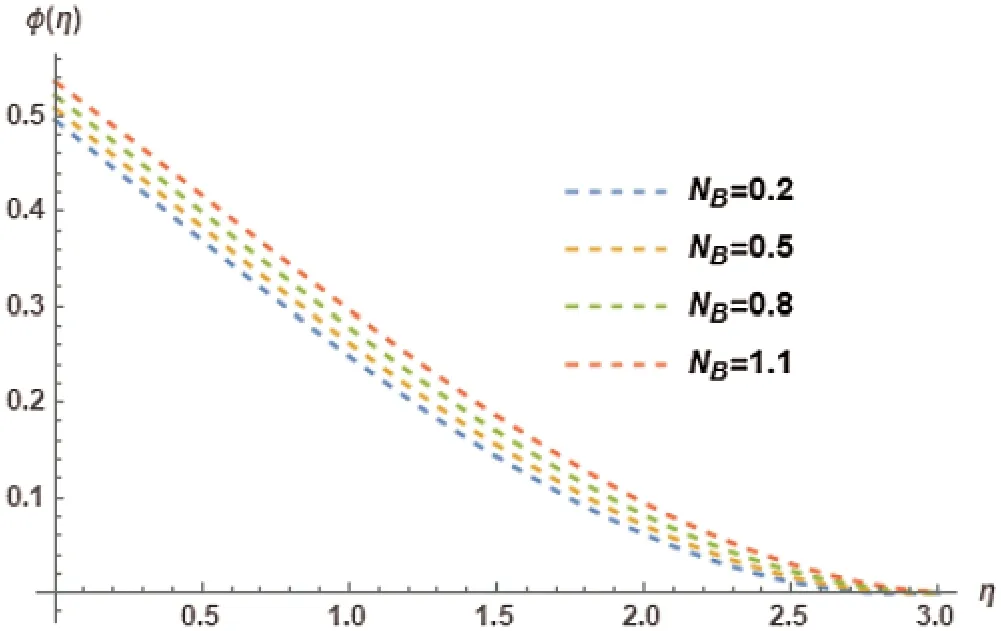
Figure 11:Influence of NB on φ(η)at M=0.5, γ = 0.5, λ= 0.5, PR=4, Kr=2, NT=0.1, LE=1,Ec=0.2, φw=1

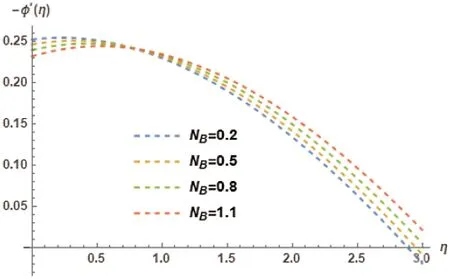
Figure 12:Variation of NB on −φ′(η)at M=0.5, γ = 0.5, λ = 0.5, PR=4, Kr=2, NT=0.1,LE=1, Ec=0.2, φw=1

Magnetic parameter’sMeffect on the temperature profileφ(η)is directed in Fig.13.It is clearly noted that an increasing trend is comprehended by theφ(η)with the increment ofM.Local Nusselt numberφ′(η)and its resultant behavior associated with the effect of magnetic parameterMis depicted in Fig.14.Magnetic parameterMcauses a decreasing trend inφ′(η).Temperature profileφ(η)association with different values of of Lewis numberLEare depicted in Fig.15.The behavioral pattern observed from the temperature profileφ(η)indicates it to be that of an increasing trend.Local Nusselts Numberφ′(η)association with the diverse values of Lewis numberLEare represented in Fig.16.The effect ofLEtriggers the decreasing trend inφ′(η)is depicted.

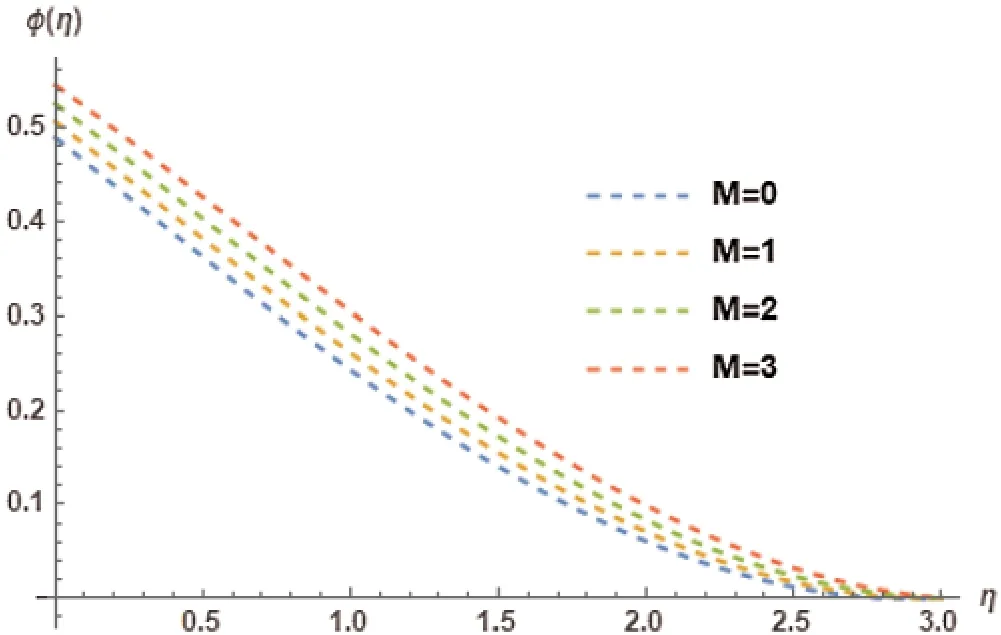
Figure 13:Temperature profile φ(η)for different choices of magnetic parameter M at Kr=3, γ =0.5, λ= 0.4, PR=3, NB=0.1, NT=0.1, LE=2, Ec=0.2, φw=1 showing their exciting nature

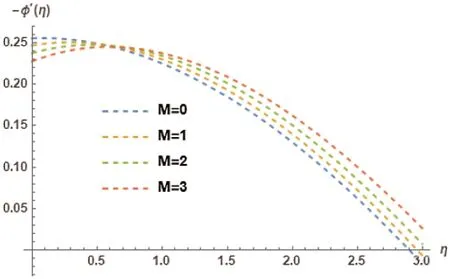
Figure 14:Nusselt number −φ′(η)for different choices of magnetic parameter M at Kr=3, γ =0.5, λ= 0.4, PR=3, NB=0.1, NT=0.1, LE=2, Ec=0.2, φw=1 showing their exciting nature

Figure 15:Temperature profile φ(η)for different choices of Lewis number LE at Kr=3, γ = 0.5,λ= 0.4, PR=3, NB=0.1, NT=0.1, M=1, Ec=0.2, φw=1 showing their exciting nature

Figure 16:Nusselt number −φ′(η)for different choices of Lewis number LE at Kr=3, γ = 0.5,λ= 0.4, PR=3, NB=0.1, NT=0.1, M=1, Ec=0.2, φw=1 showing their exciting nature

Temperature profile and its association with different values of Eckert NumberEcare represented in Fig.17.The different values ofEcinvoke an increasing trend in the temperature profileφ(η).Fig.18 showcases the effect of Eckert NumberEcon local Nusselt numbersφ′(η).The increase inEccauses an inverse influence inφ′(η).This means that an increase inEcwill cause a decrease inφ′(η).Hence,a decreasing trend is comprehended inφ′(η).The impact of Biot numberλis reviewed in Fig.19 in accordance with temperature profileφ(η).It is observed that increase in theλwill cause an increase in theφ(η).Hence an increasing trend has been comprehended in the temperature profile.Biot numberλand its impact on the local Nusselt numberφ′(η)is demonstrated in Fig.20.It is observed thatλwill cause an increase inφ′(η).Therefore,an increasing trend is triggered inφ′(η).

Figure 17:Influence of Ec on φ(η)at M=0.5, γ = 0.5, λ= 0.5, PR=4, Kr=2, NT=0.1, LE=1,NB=0.1, φw=1

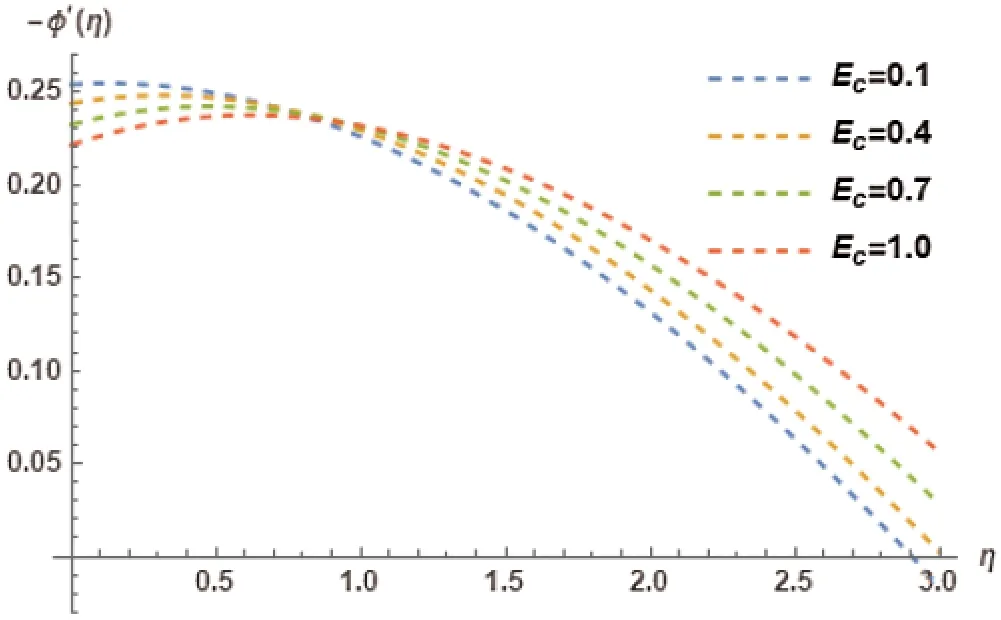
Figure 18:Variation of Ec on −φ′(η)at M=0.5, γ = 0.5, λ= 0.5, PR=4, Kr=2, NT=0.1, LE=1, NB=0.1, φw=1

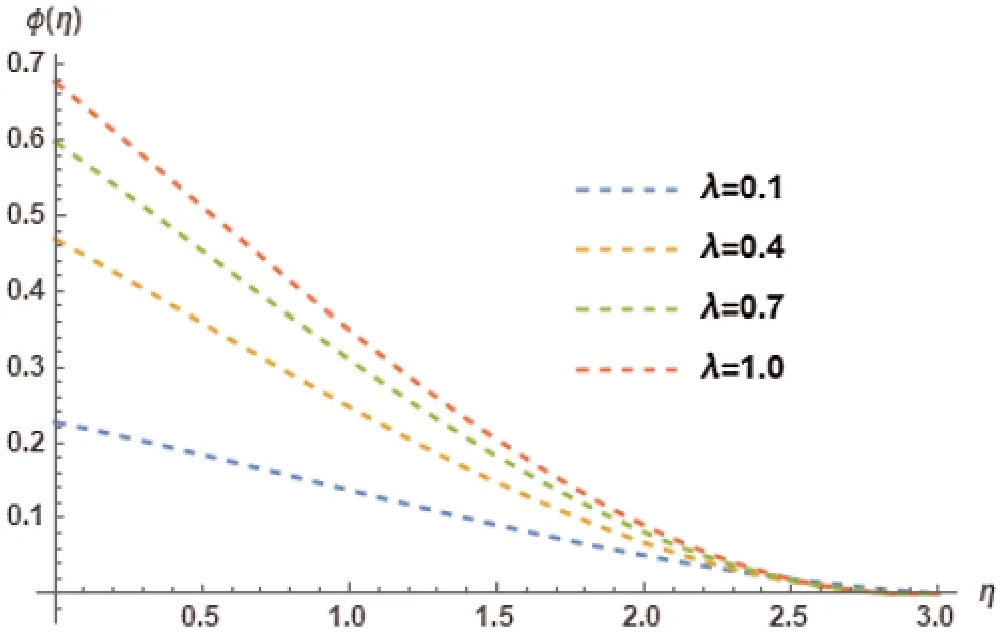
Figure 19:Influence of λ on φ(η)at M=0.5, γ = 0.5, Ec=0.4, PR=4, Kr=2, NT=0.1, LE=1,NB=0.1, φw=1

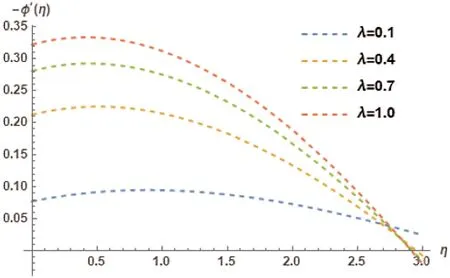
Figure 20:Variation of λ on −φ′(η)at M=0.5, γ = 0.5, Ec=0.4, PR=4, Kr=2, NT=0.1, LE=1, NB=0.1, φw=1

Figure 21:Nanoparticle concentration profile θ(η)for different choices of radiation parameter Kr at M=1, γ = 0.5, λ = 0.4, PR=3, NB=0.1, NT=0.1, LE=2, Ec=0.2, θw=1 showing their exciting nature

Fig.21 represents the Nanoparticle concentration profileθ(η)and its association with diverse values of radiation parameterKr.It is observed that the nanoparticles are elicited inversely with different variations of the radiation parameter.Thus a decreasing trend has been comprehended inθ(η).Different variations of radiation parameterKron Sherwood numberθ′(η)is shown in Fig.22.The increase inKralso originates an increase in theθ′(η).Therefore an increasing trend is comprehended inθ′(η).Different values of Prandtl numberPRin association with Nanoparticle concentration profileθ(η)are presented in Fig.23.The effect of different variations ofPRtrigger an increasing trend inθ(η).Prandtl numberPRand its different values impact on the Sherwood numberθ′(η)are revealed in Fig.24.The different values ofPRinversely effect theθ′(η).Therefore a decreasing trend is observed inθ′(η).

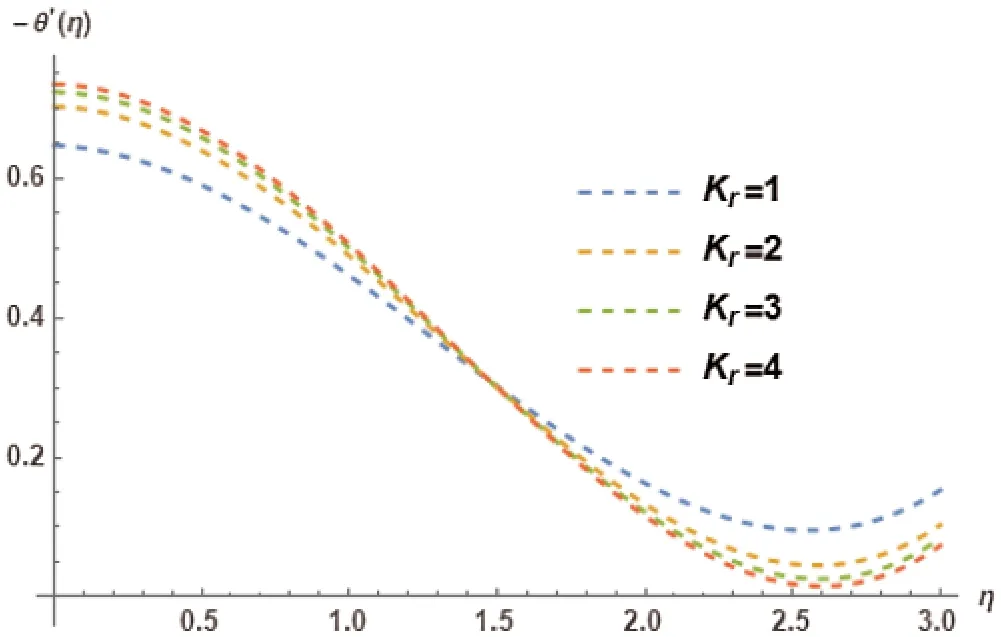
Figure 22:Sherwood number −θ′(η)for different choices of radiation parameter Kr at M=1, γ =0.5, λ= 0.4, PR=3, NB=0.1, NT=0.1, LE=2, Ec=0.2, θw=1 showing their exciting nature

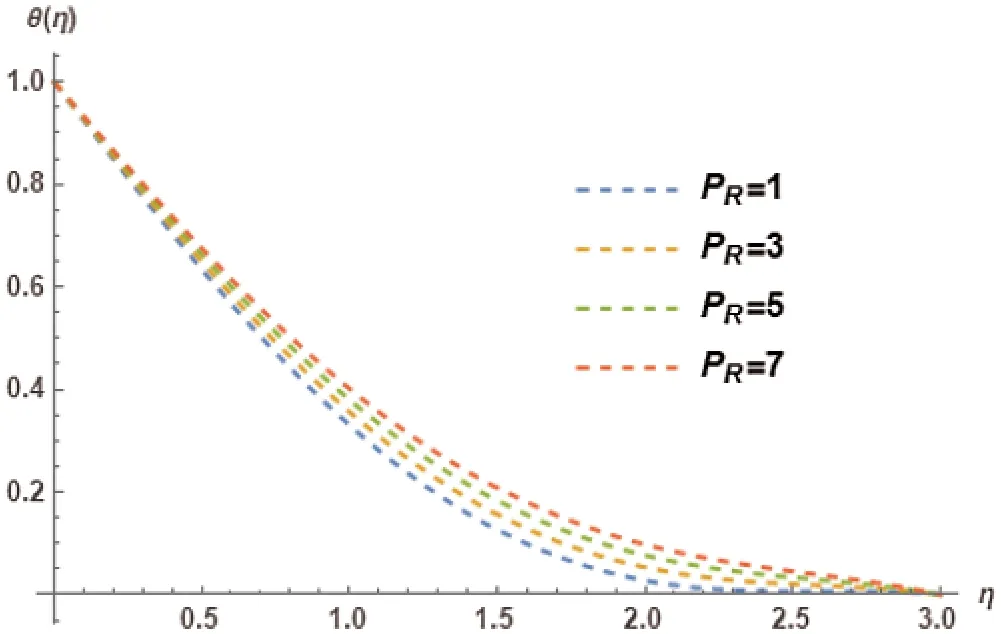
Figure 23:Nanoparticle concentration profile θ(η)for different choices of Prandtl number PR at M=0.5, γ = 0.5, λ= 0.5, Kr=2, NB=0.1, NT=0.1, LE=1, Ec=0.2, θw=1 showing their exciting nature

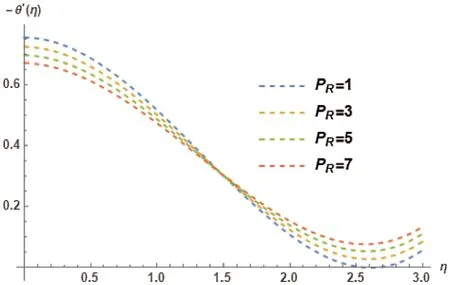
Figure 24:Sherwood number −θ′(η)for different choices of Prandtl number PR at M=0.5, γ =0.5, λ= 0.5, Kr=2, NB=0.1, NT=0.1, LE=1, Ec=0.2, θw=1 showing their exciting nature

The thermophoresis parameterNTand its association with Nanoparticle concentration profileθ(η)is represented in Fig.25.The increase inNTtriggers an increasing trend inθ(η).Different values of thermophoresis parameterNTand their impact on Sherwood numberθ′(η)is revealed in Fig.26.The different variations inNTcause a decreasing trend inθ′(η).Brownian motion parameterNBand its influence on Nanoparticle concentration profileθ(η)is discussed in Fig.27.The different variations ofNBelicit a decreasing trend inθ(η).Brownian motion parameterNBand its diverse values effect on the Sherwood numberθ′(η)are presented in Fig.28.It is observed that these variations elicit an increasing trend inθ′(η).

Figure 25:Influence of NT on θ(η)at M=0.5, γ = 0.5, λ= 0.5, PR=4, Kr=2, NB=0.1, LE=1,Ec=0.2, θw=1

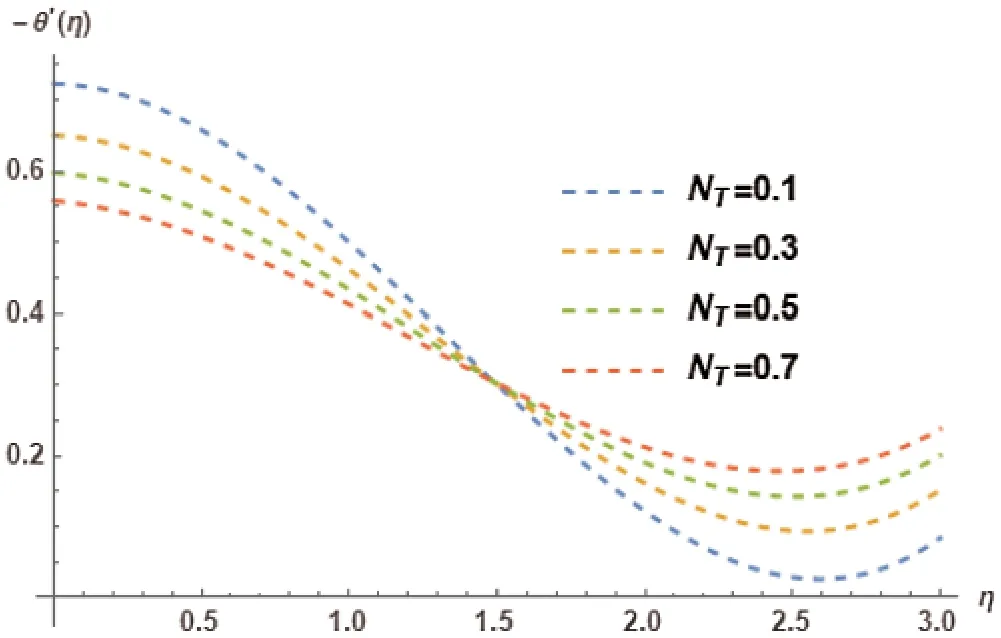
Figure 26:Variation of NT on −θ′(η)at M=0.5, γ = 0.5, λ= 0.5, PR=4, Kr=2, NB=0.1, LE=1, Ec=0.2, θw=1

Figure 27:Influence of NB on θ(η)at M=0.5, γ = 0.5, λ= 0.5, PR=4, Kr=2, NT=0.1, LE=1,Ec=0.2, θw=1

Figure 28:Variation of NB on −θ′(η)at M=0.5, γ = 0.5, λ = 0.5, PR=4, Kr=2, NT=0.1,LE=1, Ec=0.2, θw=1

Diverse values of Lewis NumberLEand their impact on the Nanoparticle concentration profileθ(η)is illustrated in Fig.29.The sudden increment inLEresulted in somewhat greater difference because of it having weaker molecular diffusivity.This indicates thatLEtriggers decreasing trend inθ(η).Lewis NumberLEand its different variations connotation with Sherwood numberθ′(η)are illustrated in Fig.30.The variations ofLEcause an increasing trend inθ′(η).The resultant values of Nanoparticle concentration profileθ(η)due to the impact of Eckert NumberEcare discussed in Fig.31.This indicates a decreasing trend inθ(η).Eckert numberEcand its diverse value’s association with the Sherwood numberθ′(η)are illustrated in Fig.32.TheEceffects the Sherwood numberθ′(η)inversely.This indicates a decreasing trend inθ′(η).Biot numberλand its diverse values impact on Nanoparticle concentration profileθ(η)is presented in Fig.33.It is observed that the Biot Numberλelicits an increasing trend inθ(η).Fig.34 shows the variation of Biot numberλon the Sherwood numberθ′(η).It is observed that the variations ofλinversely effect theθ′(η).This indicates a decreasing trend inθ′(η).

Figure 29:Nanoparticle concentration profile θ(η)for different choices of Lewis number LE at Kr=3, γ = 0.5, λ= 0.4, PR=3, NB=0.1, NT=0.1, M=1, Ec=0.2, θw=1 showing their exciting nature

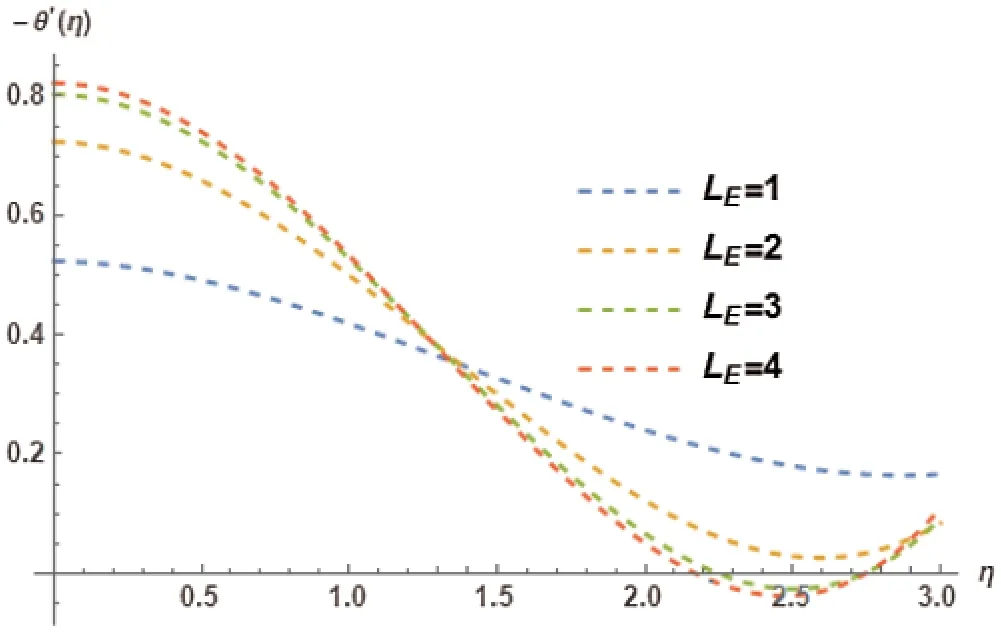
Figure 30:Sherwood number−θ′(η)for different choices of Lewis number LE at Kr=3, γ = 0.5,λ= 0.4, PR=3, NB=0.1, NT=0.1, M=1, Ec=0.2, θw=1 showing their exciting nature

Figure 31:Influence of Ec on θ(η)at M=0.5, γ = 0.5, λ= 0.5, PR=4, Kr=2, NT=0.1, LE=1,NB=0.1, θw=1

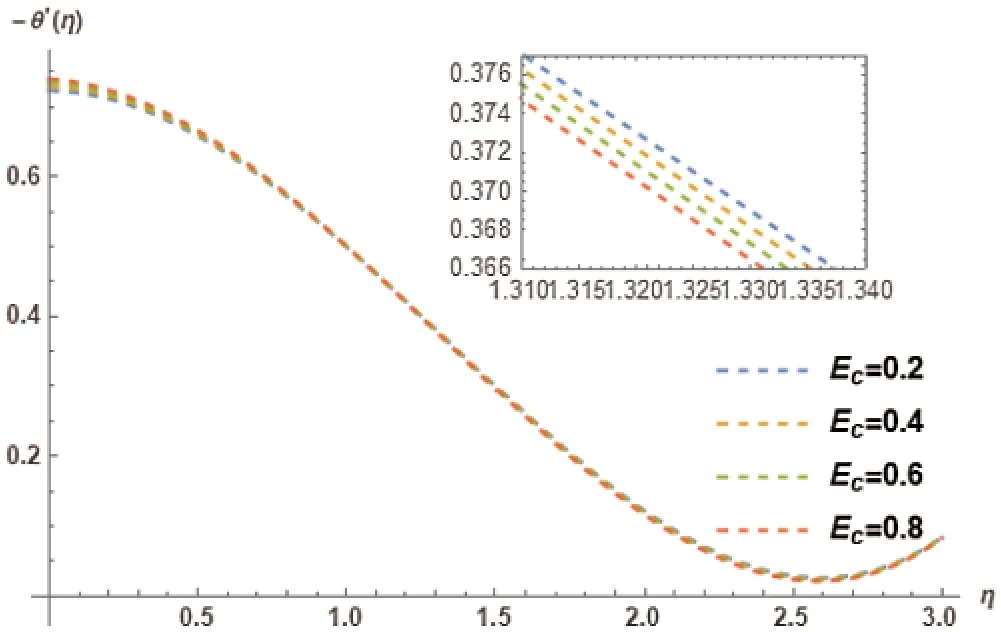
Figure 32:Variation of Ec on −θ′(η)at M=0.5, γ = 0.5, λ= 0.5, PR=4, Kr=2, NT=0.1, LE=1, NB=0.1, θw=1

Figure 33:Influence of λ on θ(η)at M=0.5, γ = 0.5, Ec=0.4, PR=4, Kr=2, NT=0.1, LE=1,NB=0.1, θw=1

Figure 34:Variation of λ on −θ′(η)at M=0.5, γ = 0.5, Ec=0.4, PR=4, Kr=2, NT=0.1, LE=1, NB=0.1, θw=1

5 Conclusion

This study exploits semi-analytical technique with changing aspects of the system.The system is based on a model with 2-D nanofluid flowing over a stretching sheet.This paper investigates the impact of Velocity profileg(η),with the magnetic parameterMand.Influence on local Nusselt numberφ′(η)and temperature profileφ(η)are also analyzed by varying magnetic field parameterM,radiation parameterKr,Brownian motion parameterNB,Prandtl numberPR,Biot numberλ,Eckert numberEc,thermophoresis parameterNT,and Sherwood numberθ′(η).The Lewis numberLEand nanoparticle concentration Profileθ(η)are also analyzed graphically.The vital interpretations are as follows:

(1)It is observed velocity profile is decreasing with the Magnetic parameterMand increasing with theγwhich is ratio betweenμ∞(x)andμw(x).

(2)Temperature profileφ(η)increases with Eckert numberEc,radiation parameterKr,thermophoresis parameterNT,magnetic parameterM,Brownian motion parameterNB,Lewis numberLE,and Biot numberλ.Temperature profile decreasesφ(η)with Prandtl numberPR.

(3)The increase in local Nusselt numberφ′(η)is invoked only with Biot numberλand Prandtl numberPR.The decrease in local Nusselt numberφ′(η)is invoked with magnetic parameterM,radiation parameterKr,Lewis numberLE,Brownian motion parameterNB,thermophoresis parameterNT,and Eckert numberEc.

(4)Nanoparticle concentration profileθ(η)increased with Biot numberλ,thermophoresis parameterNTand Prandtl numberPR.Decreasing trend for Nanoparticle concentration profileθ(η)was observed with Brownian motion parameterNB,Lewis numberLE,and Eckert numberEcand radiation parameterKr.

(5)Trend for Sherwood numberθ′(η)was observed to increase with radiation parameterKr,Lewis numberLE,and Brownian motion parameterNB.Trend for Sherwood numberθ′(η)was observed to decrease with Eckert numberEc,thermophoresis parameterNT,Biot numberλand Prandtl numberPR.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.