Performance Analysis of Magnetic Nanoparticles during Targeted Drug Delivery:Application of OHAM

Muhammad Zafar,Muhammad Saif Ullah,Tareq Manzoor,Muddassir Ali,Kashif Nazar,Shaukat Iqbal,Habib Ullah Manzoor,Rizwan Haider and Woo Young Kim

1Institute of Energy and Environmental Engineering,University of the Punjab,Quaid-e-Azam Campus,Lahore,54590,Pakistan

2Energy Research Centre,COMSATS University Islamabad,Lahore,54000,Pakistan

3Department of Energy Engineering,Faculty of Mechanical and Aeronautical Engineering,University of Engineering and Technology,Taxila,47080,Pakistan

4Department of Mathematics,COMSATS University Islamabad,Lahore,54000,Pakistan

5School of Systems and Technology,University of Management Sciences and Technology,Lahore,54770,Pakistan

6Departmentof Electrical,Electronics and TelecommunicationEngineering,University of Engineering and Technology,Lahore(FSD Campus),Faisalabad,38000,Pakistan

7Department of Electronic Engineering,Faculty of Applied Energy System,Jeju National University,Jeju Special Self-Governing Province,Jeju-si,63243,Korea

ABSTRACT In recent years,the emergence of nanotechnology experienced incredible development in the field of medical sciences.During the past decade,investigating the characteristics of nanoparticles during fluid flow has been one of the intriguing issues.Nanoparticle distribution and uniformity have emerged as substantial criteria in both medical and engineering applications.Adverse effects of chemotherapy on healthy tissues are known to be a significant concern during cancer therapy.A novel treatment method of magnetic drug targeting (MDT)has emerged as a promising topical cancer treatment along with some attractive advantages of improving efficacy,fewer side effects,and reduce drug dose.During magnetic drug targeting,the appropriate movement of nanoparticles(magnetic)as carriers is essential for the therapeutic process in the blood clot removal,infection treatment,and tumor cell treatment.In this study,we have numerically investigated the behavior of an unsteady blood flow infused with magnetic nanoparticles during MDT under the influence of a uniform external magnetic field in a microtube.An optimal homotopy asymptotic method (OHAM)is employed to compute the governing equation for unsteady electromagnetohydrodynamics flow.The influence of Hartmann number(Ha),particle mass parameter(G),particle concentration parameter (R),and electro-osmotic parameter (k)is investigated on the velocity of magnetic nanoparticles and blood flow.Results obtained show that the electro-osmotic parameter,along with Hartmann’s number,dramatically affects the velocity of magnetic nanoparticles,blood flow velocity,and flow rate.Moreover,results also reveal that at a higher Hartman number,homogeneity in nanoparticles distribution improved considerably.The particle concentration and mass parameters effectively influence the capturing effect on nanoparticles in the blood flow using a micro-tube for magnetic drug targeting.Lastly,investigation also indicates that the OHAM analysis is efficient and quick to handle the system of nonlinear equations.

KEYWORDS Hartmann number; magnetic nanoparticles; nonlinear analysis; targeted drug delivery; optimal homotopy asymptotic method (OHAM)

1 Introduction

Nanotechnology is effectively playing its significant role in numerous fields such as structure,environment,molecular physics,chemistry,biology,material sciences,computer sciences,engineering,measurements,imaging,and many other disciplines of science and technology [1-6].Likewise,the application of nanoparticles for drug delivery is also one of the critical forefronts of medical sciences.The use of nanoparticles or nanotubes,as detectors or biosensors,can be exploited as they suffer changes in their respective electrical properties upon application.Moreover,under the influence of the magnetic field,such particles can be called as magnetic nanoparticles.

Magnetic nanoparticles typically consist of nickel,cobalt,or iron and are clusters of magnetic particles where several individual particles are present.By the application of synthesized Fe3C,magnetic hyperthermia can be studied.Similarly,the intrinsic loss power value and a specific absorption rate can also be determined.It is a well-known fact that these aspects are much superior at lower magnetic nanoparticle concentrations [7].

Since blood can be considered a bio-magnetic fluid,prone to be affected upon the magnetic field’s application,the exploitation of magnetic fluid properties can help improve drug targeting through the transportation of magnetic particles in the blood [8].The application of magnetic nanoparticles in biomedicine offer advantages of stability and size controllability of magnetic nanoparticles.The magnetic nanoparticle applications have been investigated in several diseases such as cardiovascular,endovascular,drug targeting,cancer tissues,and hyperthermia treatment for malignant tumor cells [9-11].It has been investigated that the blood’s viscosity with magnetic particles caries from the blood under the magnetic field’s influence [12].The magnetization of fluid under the magnetic field’s control,without the electric field’s induction,affects bio-magnetic fluid flow [12-15].However,most of these studies did not account for the instability of blood flow [16].Various mathematical models considered that the blood flow followed non-Newtonian fluid properties.The study of non-Newtonian blood flow characteristics in micro-tube under the magnetic field’s influence is carried out by Shaw et al.[17].However,Bandyopadhyay et al.[18]studied the Newtonian model for investigating the blood flow through a constricted channel.More interestingly,Shit et al.[19] studied the pulsatile blood flow in an artery environment under the influence of magnetic dipole.Considering Newtonian fluid properties,various studies are conducted to investigate the transportation of magnetic nanoparticles,capture efficiency in a tube for targeted drug delivery,and the effect of nanoparticle augmentation [20-25].The majority of these studies are focused on pressure gradient and electrokinetic force,which necessitated the further exploration of magnetic nanoparticles and blow,together,in a channel,under the influence of the magnetic field,electrokinetic force,and pressure gradient.

Recently,a semi-analytic approximate method emerged for handling time-dependent partial differential equations,known as the optimal homotopy asymptotic method (OHAM).Compared to numerical methods,the optimal homotopy asymptotic method (OHAM)is powerful and straightforward.It achieves outcomes more quickly while maintaining acceptable results and good agreement with numerical methods.This method combines the advantages of the homotopy principle with an efficacious computational algorithm that gives a thorough and straightforward approach for controlling solution convergence [26-28].The main advantage of OHAM is that it is free of parameters,does not require identifying the ħ-curve and any guess initial like in other methods.Moreover,the OHAM consists of inherent convergence criteria like the homotopy analysis method (HAM),with greater flexibility [29].The OHAM is not only applicable for small parameters,but it also demonstrates its reliability and high accuracy to solve nonlinear systems in engineering and science.There are also few disadvantages of the OHAM.One of the disadvantages is that a set of nonlinear algebraic equations must be solved in each order of approximations.Another limitation is that OHAM consists of several unidentified convergencecontrol variables,making computations time-consuming [30].Several nonlinear coupled partial and ordinary differential systems can be accurately solved using this approach.Many recent studies have considered using this technique to solve a variety of nonlinear problems [31-33].However,to the best of the authors’knowledge,no attempt is made to investigate magnetic particles and blood movement through a micro-tube under the influence of external forces using the OHAM.

The present study provides insight into the movement of magnetic nanoparticles in a tube with blood flow under the collective effect of the electrokinetic force,magnetic field,and pulsatile pressure gradient.It is well-established that the ability to predict the capture of nanoparticles under the influence of a magnetic fieldin vivois essential.In this study,we solved the governing equations to predict blood flow and magnetic particle velocity using the optimal homotopy asymptotic method approach.The parametric study is used here to compute the solutions for the non-dimensional velocity of magnetic particles and blood.These studies’findings may further explore magnetic therapy viability with magnetic nanoparticles to help design medical devices and drug delivery systems for blood clot removal,infection treatment,and tumor cell treatment.

2 Methodology

2.1 Mathematical Formulation

In the current study,a two-dimensional mathematical formulation based on an unsteady and incompressible blood flow together with magnetic nanoparticles in a cylindrical vessel under the presence of a uniform external magnetic field and an axial electric field is considered.The schematic illustration of the physical problem is presented in Fig.1,where ther∗is the radial coordinate perpendicular to flow direction.Thez∗axis is taken along the vessel’s axis.The length and radius of the vessel are taken asLand h,respectively.It is assumed that the flow is axisymmetric and developed fully.A coherent magnetic field is employed perpendicular to the direction of the flow.It is also assumed that the wall zeta potential is constant in an electrolyte solution of blood near the vessel wall.The pressure gradient(∂p∗/∂z∗)is applied along the axis of the vessel and a no-slip boundary on the wall of the vessel.It is assumed that the micro-vessel length is significantly larger than its radius,and the magnetic nanoparticles are uniformly dispersed in the bloodstream.For this case,the magnetic Reynolds number (Rem=vref lref/vm,wherevrefis the reference velocity,lrefis the reference length scale andvmis the magnetic diffusivity)is very low (Rem<<1),and hence the effect of the induced magnetic field can be neglected during the present study.

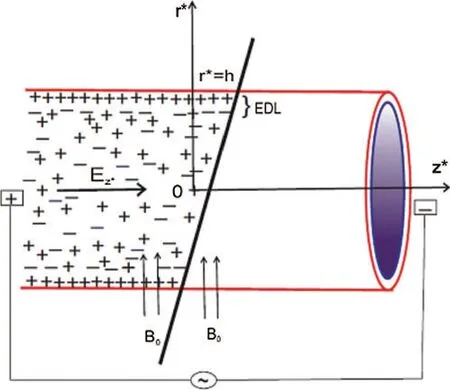
Figure 1:Schematic representation of the physical problem (Reproduced with permission from A.Mondal and G.C.Shit,Journal of Magnetism and Magnetic Materials; published by Elsevier B.V.,2017)

2.1.1 Distribution of Electrical Potential

For at any point(r∗,z∗)in the vessel,the total electric potential(φ∗)is written as [16]

whereψ∗(r∗)andEz∗are the potential distribution due to the presence of an electrical double layer (EDL)and applied electric field,respectively.Electrical potential distribution within the cylindrical coordinate is defined using the famous Poisson equation form

whereρeand∊is the net charge density and permittivity of the medium,respectively.

The overall charge density distribution can be given as the sum of all cations and anions in the solution,assuming the equilibrium Boltzmann distribution,

wherezi,e,no,kB,andTavare the valence of typeiions,a charge of an electron,bulk ionic concentration,Boltzmann constant,and absolute temperature,respectively.Assume that the thermal energy of the ions is much larger than the electric potential,i.e.,≪1,for which the Debye-Hückel linearization principle can be estimated asAccording to this assumption,the overall charge density is the electric charge density can be further expressed as

Accordingly,Eq.(2)can be rewritten as

where 1/λDis known as Debye length (EDL thickness)and is described asThe corresponding boundary conditions are applied toψ∗(r∗)are

Now,introducing a normalized electro-osmotic potential functionψconsisting of zeta potentialξof the medium and the non-dimensional coordinates in the form

wherehis the characteristic radius of the micro-vessel.

In terms of the non-dimensional variables described in Eqs.(5),(7)gives

wherek=h/λDis known as the electro-osmotic parameter.The non-dimensional form of the corresponding boundary conditions (6)is expressed as

The electric potential distribution solution from the Eq.(8)by Eq.(9)can be given in the form of the modified Bessel function of the first kind as

whereIois known as the zeroth-order modified Bessel function of the first kind.

2.1.2 Flow Investigation

The flow of blood together with the magnetic nanoparticle velocity inside a micro-vessel(assuming cylindrical polar coordinates)is expressed by the governing equation of electron magnetohydrodynamic [22,34,35]

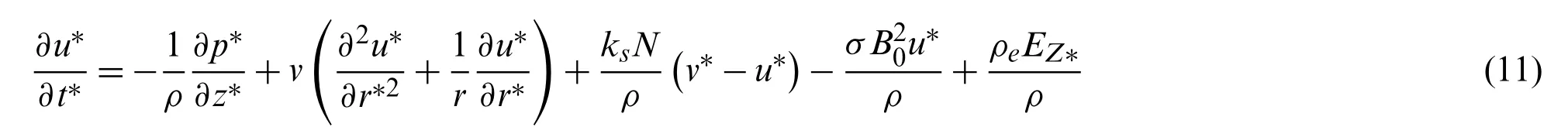
We assumed that a spherical magnetic nanoparticle motion in a viscous carrier fluid is governed by the applied magnetic and electric field effect.The viscous drag and magnetic forces during slow motion are responsible forces,and thus ignoring the Brownian motion,the movement of the nanoparticles is given by the second law of motion (Newton’s)[35-38].

wherem(=4/3πr3pρpwith a particle radiusrpand particle densityρp)is a single nanoparticle mass,v∗(r∗,t∗)is a single magnetic nanoparticle velocity,u∗(r∗,t∗)is the axial velocity of blood,Bois the strength of the applied magnetic field,p∗is the fluid pressure,ρis the blood density,vis the kinematic viscosity coefficient,σis the electrical conductivity,Nis the magnetic nanoparticles number per unit volume andKs=6πμEhyd,pVr(with an effective hydrodynamic radius of the particleEhyd,pand magnetic drift velocityVr)is Stokes constant [36].The terms on the right side of the Eq.(11)are the forces resulting from the relative motion between magnetic nanoparticles and fluid,the Lorentz force due to the magnetic field and the net electrical body force.The termsFm,Ff,andFeon the right side of Eq.(12)are the magnetic,fluidic,and electric forces,respectively.

If the mass of a particle is likely to be negligible,the inertia termcan be neglected,and therefore the motion of the particle must fulfill the force balanceFm+Ff+Fe=0.

By using Stoke’s law for the drag on a sphere,the fluidic force encountered by a particle(considering low Reynolds number)is estimated by

If the force acting on the particle is fluidic in one dimension [22,36],i.e.,Ffexpressed by Eq.(13),the Eq.(12)becomes

Along the axial direction the pulsatile pressure gradient can be given as [18]

where ω′is the pulsation frequency,A0is the pressure gradient constant amplitude,andA1is the pulsatile component amplitude that increases periodic pressure in a micro-vessel.

The boundary conditions for magnetic nanoparticles and fluid velocity can be put mathematically in the form of

The following non-dimensional variables can be introduced as

withUHS=−∊Ez∗ξ/μis the classical electro-osmotic flow velocity,also known as the Helmholtz-Smoluchowski velocity [39].In this case,non-dimensional variables described in Eq.(17),the Eqs.(11)and (14)take the following form:

and non-dimensional boundary conditions take the following form:

The dimensionless mathematical expression for the wall shear stress (WSS)τwand volumetric flow rateQis given as,respectively

2.1.3 Numerical Method

The optimal homotopy analysis method for the equation is as follows [40]:

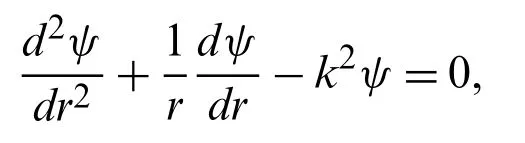
with boundary conditions

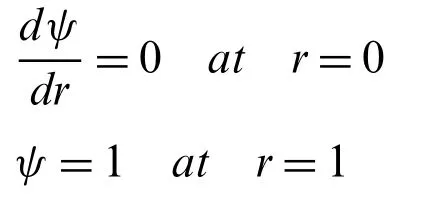
2.1.4 Principle of OHAM

This section describes the OHAM principle,and the following differential equation can be used to demonstrate the basic concept of the OHAM.

It depends on the following boundary condition:B(u)=0.

First of all,build a series of equations using the OHAM [41,42]

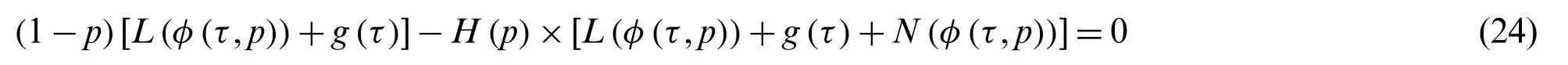
with the boundary condition

wherep∈[0,1],φ(τ,p),andH(p)are the embedded parameter,unknown function,and nonzero auxiliary function forp≠0 andH(0)=0,respectively.Thus,atp=0 andp=1,it follows that

Accordingly,asprises from 0 to 1,the initial solutionu0(τ)moves closer to solutionu(τ).Now,

The auxiliary function can be considered now,which can be expressed in the following way:

whereC1,C2,C3are the constants,which will be later decided.

In the following way,expandingφ(τ,p)in a series in terms ofp

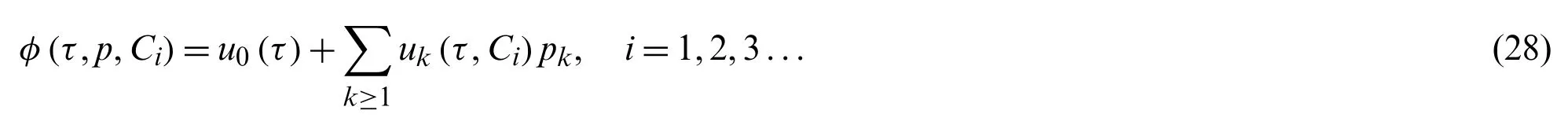
A series of differential equations with boundary conditions are derived by putting Eq.(28)into Eq.(24),gathering the same power ofpand equating the coefficient of like powerpto zero.As a result,by solving a differential equation with boundary conditions,we getu0(τ),u1(τ,C1),u2(τ,C3),...etc.In general,the solution of Eq.(23)can be approximated in the following way:

The following expression for residual is obtained by substituting Eq.(29)in Eq.(23)

At length a servant arrived and led him up into a beautiful room filled with people, who were either playing on musical instruments or talking in a lively manner, which astonished the king, who stood silently listening, and not at all pleased at the want of attention paid him

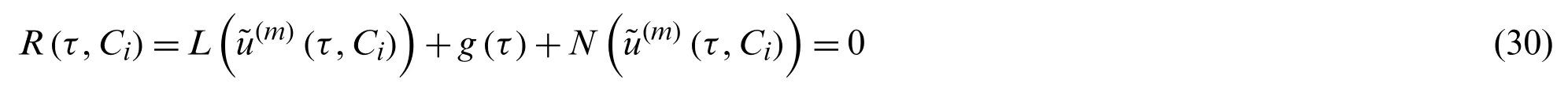
IfR(τ,Ci)=0 then(τ,Ci)represents the precise solution to the problem.In most cases,especially in nonlinear problems,this does not occur,but we can reduce the functional

The constantsCiare obtained using the following conditions:

These constants are used to determine the approximate solution (of order m)from Eq.(29).

2.1.5 Application of OHAM

This section describes the OHAM application to the differential Eq.(3).Moreover,we can build homotopy of the Eq.(3)according to the OHAM [39] as follows:

Consideringψas follows:

then putting the value ofψfrom the Eq.(5)into Eq.(4),and assuming some simplifications and reorganizing according to powers of p-terms,it forms as

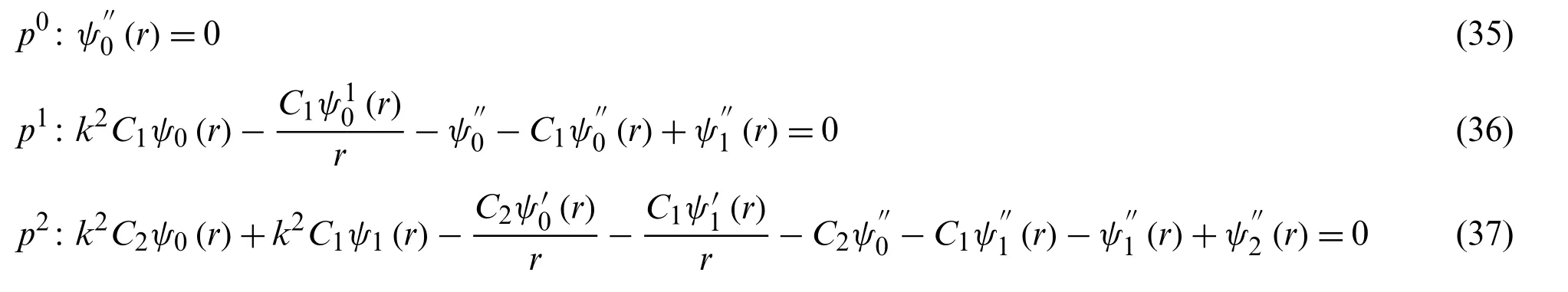
with the conditions

ψ′0(0)=0,ψ0(1)=1

we get from Eq.(35)

ψ0(r)=1

and similarly with the conditions

ψ′1(0)=0,ψ1(1)=0

we getψ1from Eq.(36)

Now forψ2(r),with the conditions

ψ′2(0)=0,ψ2(1)=0

we getψ2from Eq.(37)

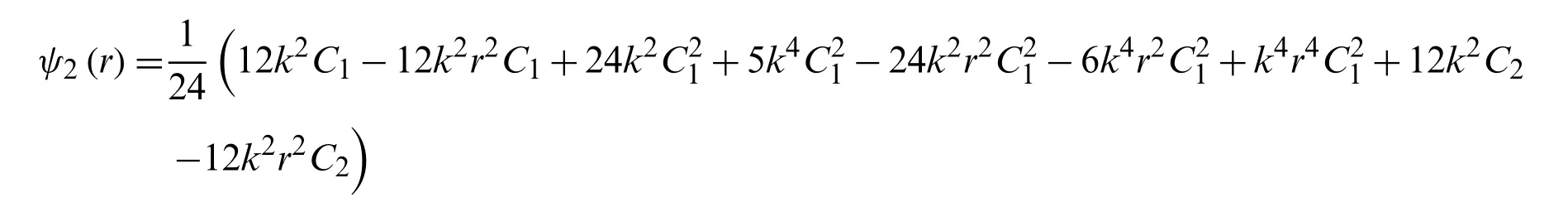
Hence the value ofψ(r)is determined from the Eq.ψ(r)=ψ0(r)+ψ1(r)+ψ2(r)is

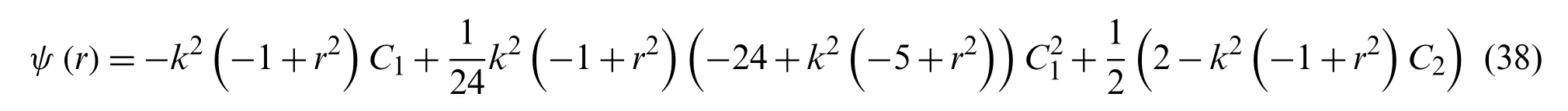
By the method of least squares,the expression for residual becomes

The values of constantsC1andC2are obtained by setting

which give the following values of constants

{{C1→0.450322,C2→−1.92525},{C1→0,C2→−0.290698},{C1→−0.450322,C2→−0.12396}}.

Assuming the values ofC1=−0.4503218 andC2=−0.1239597,based on these values,the calculatedψis

Now for the Eqs.(18)and (19)with boundary conditions

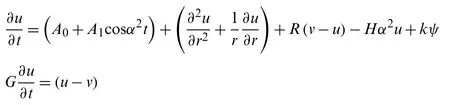
with boundary conditions

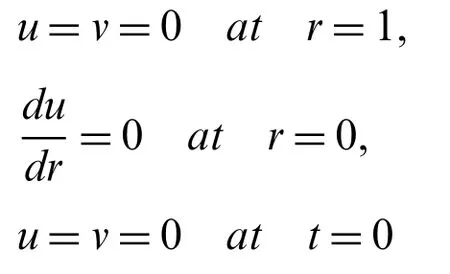
with

and

According to OHAM for Eq.(42)

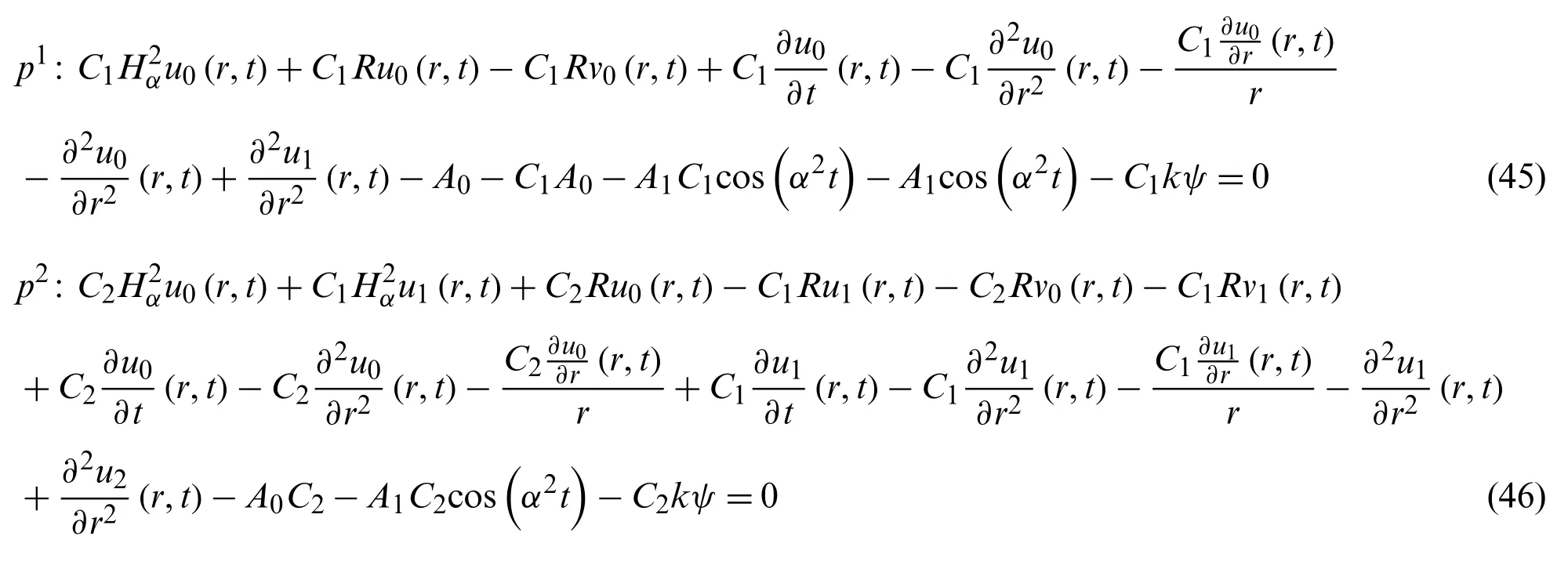
Now the formulation of OHAM for Eq.(43)

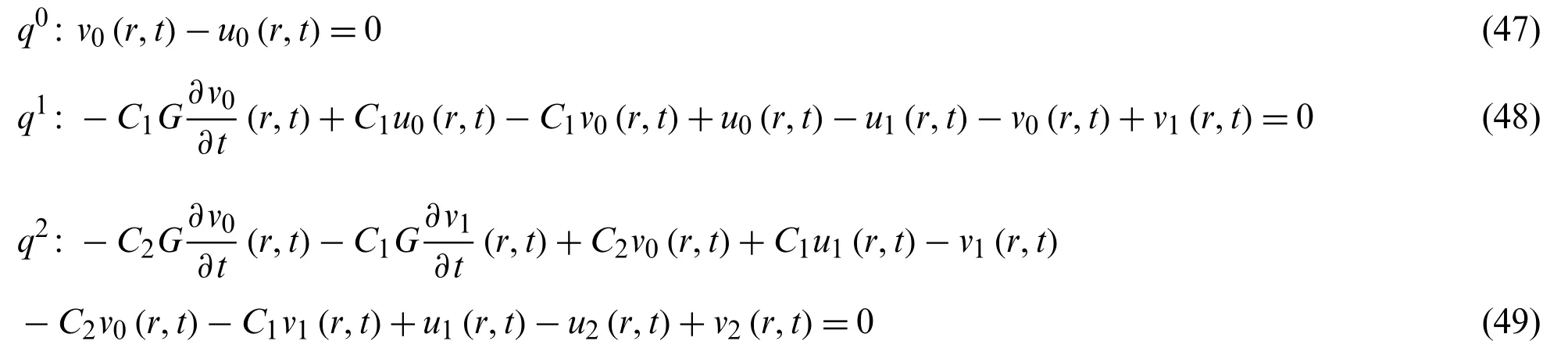
with the conditions

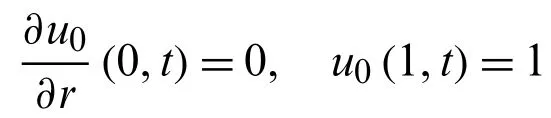
we get from Eq.(44)

now with the conditions

we get from Eq.(45)

foru2(r,t),with the following conditions

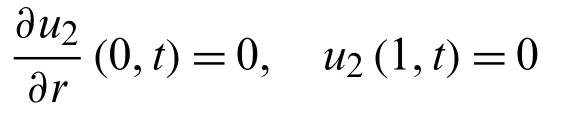
we get from Eq.(46)

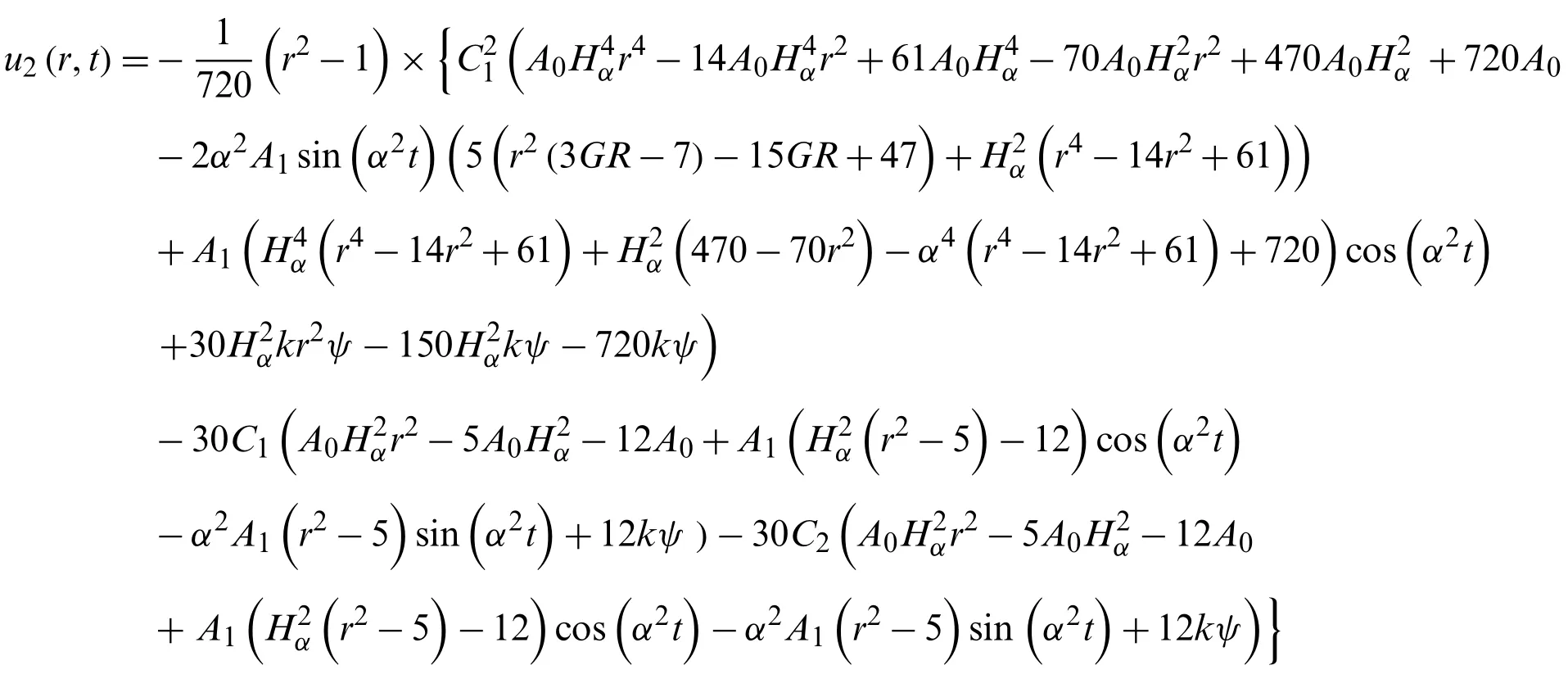
now the equation

u=u0(r,t)+u1(r,t)+u2(r,t)

Becomes

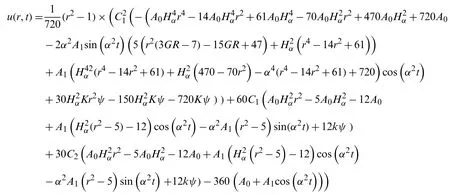
Now using the relationship

v0(r,t)−u0(r,t)=0

we get

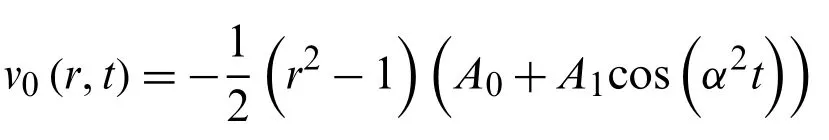
Again using the relationship

gives

Similarly with

we get

Now with the equation

v(r,t)=v0(r,t)+v1(r,t)+v2(r,t)

gives

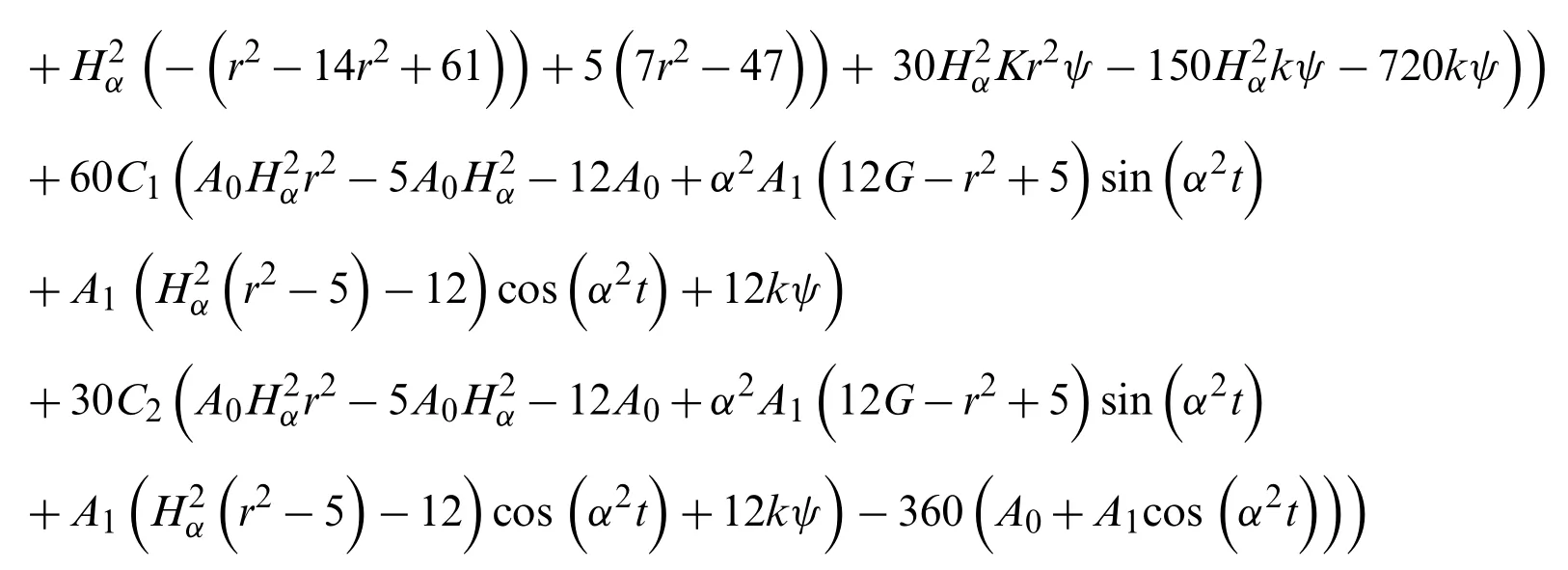
The residue term for the functionu(r,t)is

Now from Eq.(31),the value is taken.And,the functionv(r,t)of the residue term is

R2=Gv1t−u+v

The description of the process for the initial guess required to initiate the OHAM process is given in detail somewhere else [31-33].

2.1.6 Non-Dimensional Velocity of the Blood

Using the least square method

and with the setting

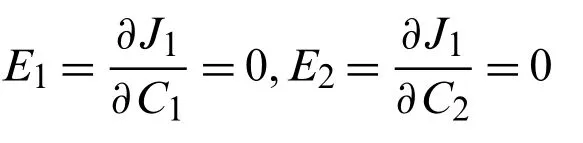
various values ofHawere obtained from the followingC1andC2,as given in Table 1.The values ofC1andC2correspond to the values ofu(r,t),which were obtained from the Eqs.(50)-(53),

Now withG=0.8 andk=2,the values ofC1andC2estimated are given in Table 2,

Table 1:Values of C1, C2,and Ha

Table 2:Values of C1, C2,and Ha

The values ofC1andC2correspond to the values ofu(r,t),which were obtained from the Eqs.(54)-(57),

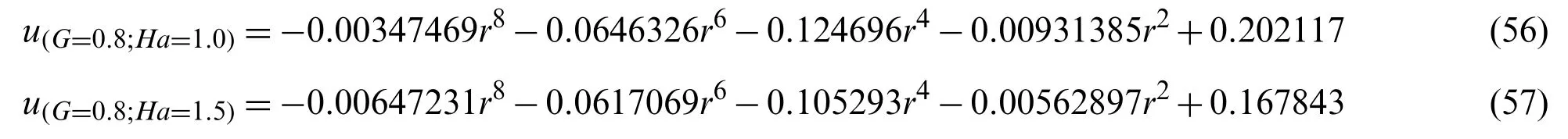
The values ofC1andC1given in Table 3 correspond to the values ofu(r,t),which were obtained from the Eqs.(58)-(61),

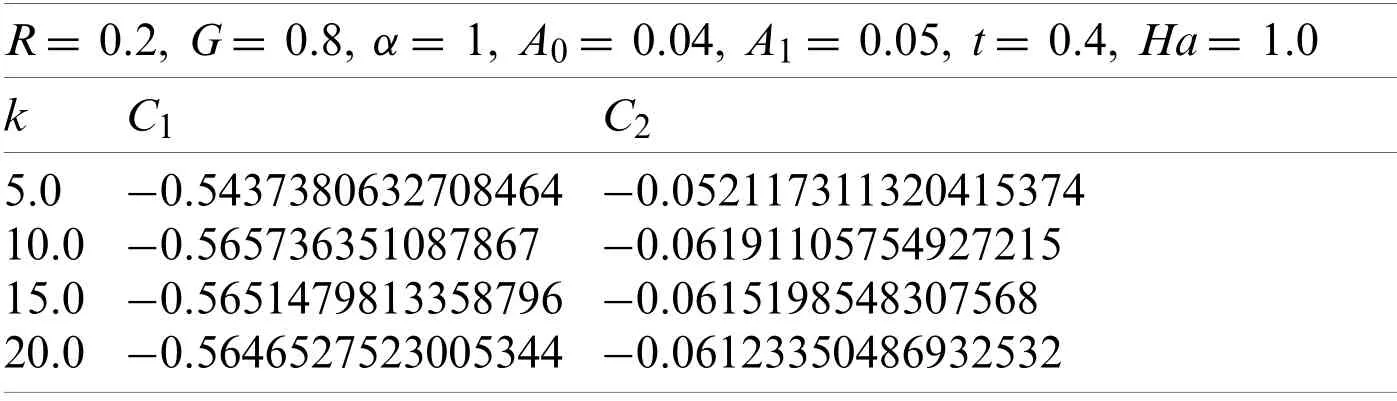
Table 3:Values of C1, C2,and k

Now changeR=0.8 and keep the other values constant,employing the similar process as earlier.The obtained values ofC1andC2are given in Table 4.

Table 4:Values of C1, C2,and k

The values ofC1andC2correspond to the values ofu(r,t),which were obtained from the Eqs.(62)-(65),

2.1.7 Non-Dimensional Velocity of the Magnetic Particles

Here withG=0.2,α=1,A0=0.04,A1=0.05,t=0.4,k=2,and R=0.5.Using the similar technique as earlier,the obtained values ofC1andC2are given in Table 5.

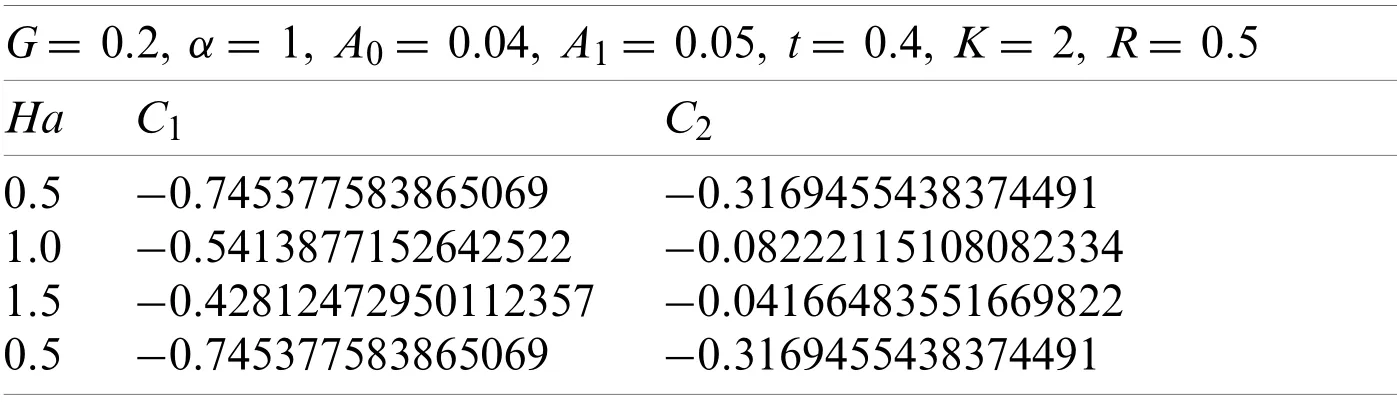
Table 5:Values of C1, C2,and Ha

The values ofC1andC2correspond to the values ofv(r,t),which were obtained from the Eqs.(66)-(69),

Here withG=0.8,α=1,A0=0.04,A1=0.05,t=0.4,k=2,andR=0.5.Using the similar technique as earlier,the obtained values ofC1andC2are given in Table 6.

Table 6:Values of C1, C2,and Ha

The values ofC1andC2correspond to the values ofv(r,t),which were obtained from the Eqs.(70)-(73),

Now withG=0.2,α=1,t=0.4,A0= 0.04,A1= 0.05,Ha=1.0,and R=0.2.Using the similar technique as earlier,for various values ofk,the obtained values ofC1andC2are given in Table 7.The calculated values ofC1andC2correspond to the values ofv(r,t),which were obtained from the Eqs.(74)-(77).

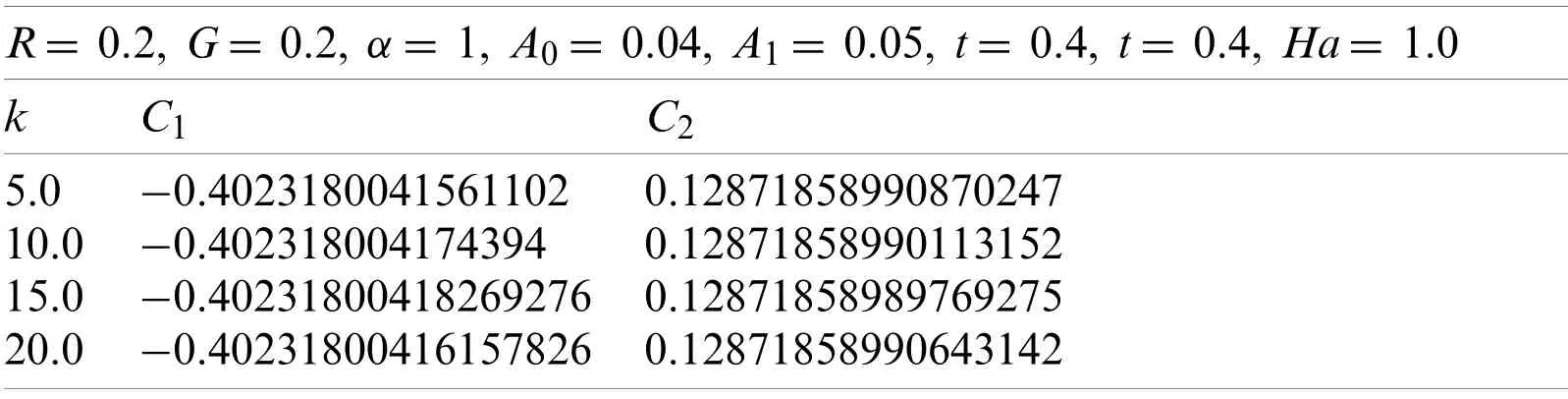
Table 7:Values of C1, C2,and k

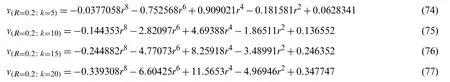
Now withG=0.8,α=1,t=0.4,A0=0.04,A1=0.05,Ha=1.0,and R=0.2.Using the similar procedure as earlier,for various values of k,the following values ofC1andC2were estimated as given in Table 8.The values ofC1andC2correspond to the values ofv(r,t),which were obtained from the Eqs.(78)-(81).

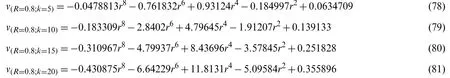
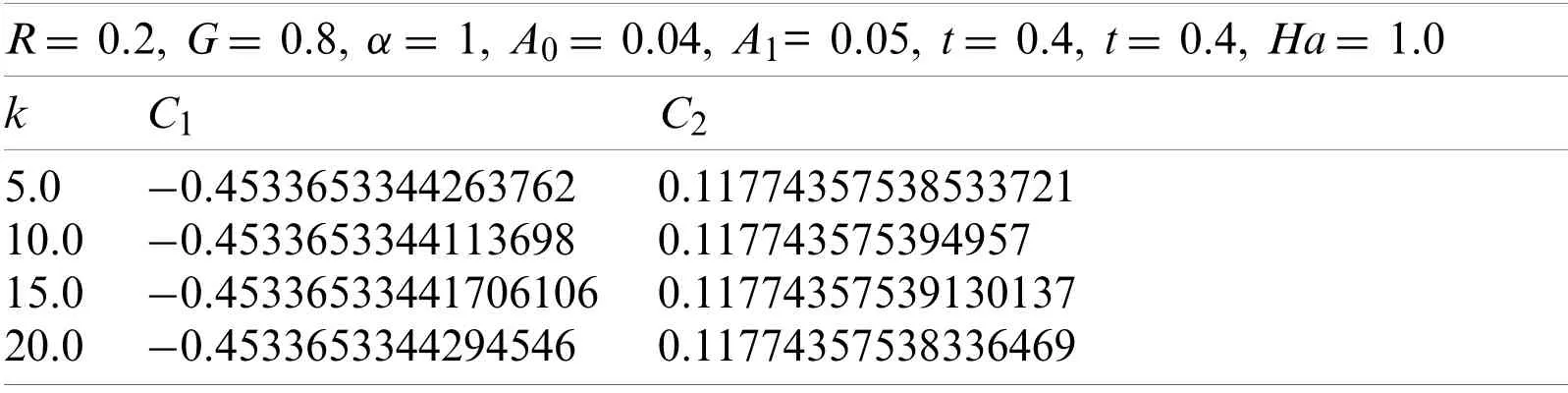
Table 8:Values of C1, C2,and k

2.1.8 Physical Properties

Values of various physical parameters and properties used during this study are given in Table 9.

Table 9:Physical parameters/properties

3 Results and Discussion

3.1 Non-Dimensional Velocity of the Blood as a Function of Ha at G=0.2

In Fig.2,the Hartmann number (Ha)influence was studied at four different values; however,the particle mass parameter (G)was 0.2.The non-dimensional velocity (u)of the blood varied at various values ofHa,but at the end,velocity converged atr=1.

3.2 Non-Dimensional Velocity of the Blood as a Function of Ha at G=0.8

In Fig.3,the Hartmann number (Ha)effect was studied at four different values; however,the particle mass parameter (G)was kept at 0.8.Figs.2 and 3 showed a similar trend despite increasingG,i.e.,0.8.Fig.2 described the influence ofHaon the non-dimensional velocity of the blood.The blood’s non-dimensional velocity varied at various values ofHa,but in the end,velocity converged atr=1.

3.3 Non-Dimensional Velocity of the Blood as a Function of k at R=0.2

In Fig.4,the effect of an electro-osmotic parameter (k)was studied at four different values;however,the particle concentration parameter (R)was kept at 0.2.Fig.4 trend was sinusoidal except at the curve wherek=5.The figure described the effect of varyingk(from 5 to 20 with increments of 5)on the non-dimensional velocity of the blood.The non-dimensional velocity of blood changed as sinusoidal at four various values ofk,but in the end,velocity converged atr=1.It can be seen that the velocity declined askrises untilr=0.3,and the final solution converged atr=0.3.Hereafter,the velocity once more dropped then rises up tor=0.8,where the curves converged,rose over with the last drop,and ultimately converged atr=1.

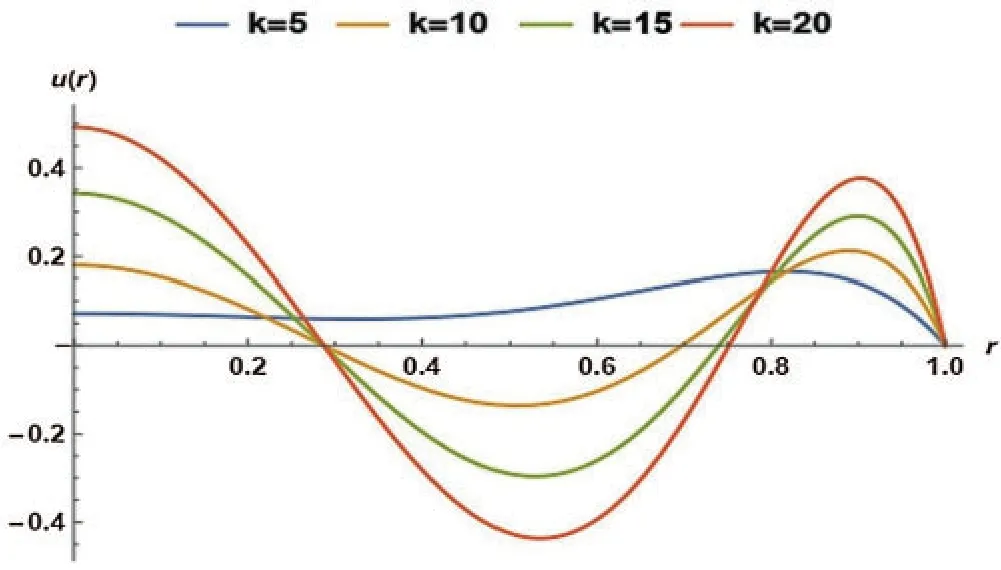
Figure 4:Non-dimensional velocity of the blood as a function of k at R= 0.2

3.4 Non-Dimensional Velocity of the Blood as a Function of k at R=0.8

In Fig.5,the effect of an electro-osmotic parameter (k)was studied at four different values;however,the particle concentration parameter (R)was kept constant at 0.8.Fig.5 trend was sinusoidal except at the curve wherek=5.The figure described the effect of varyingk(from 5 to 20 with increments of 5)on the non-dimensional velocity of the blood.The non-dimensional velocity of blood changed as sinusoidal at four various values ofk,but in the end,velocity converged atr=1.It can be seen that the velocity declined asKrises untilr=0.3,and the final solution converged atr=0.3.Hereafter,the velocity once more dropped then rises up tor=0.8,where the curves converged,rose over with the last drop,and ultimately converged atr=1.

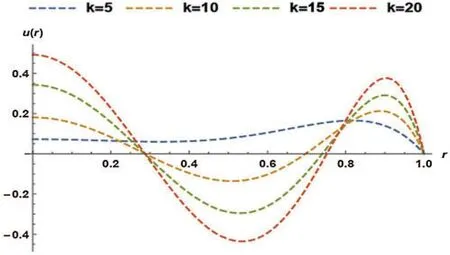
Figure 5:Non-dimensional velocity of the blood as a function of k at R= 0.8

3.5 Non-Dimensional Velocity of the Magnetic Particles as a Function of Ha at G=0.2

In Fig.6,the Hartmann Number effect was studied at four different values; however,the particle mass parameter (G)was kept constant at 0.2.The magnetic particle’s velocity (v)varied at four variousHavalues,but in the end,velocity converged atr=1.The velocity of magnetic particles declined as the Hartmann number increased from 0.5 to 2.0 (with increments of 0.5).

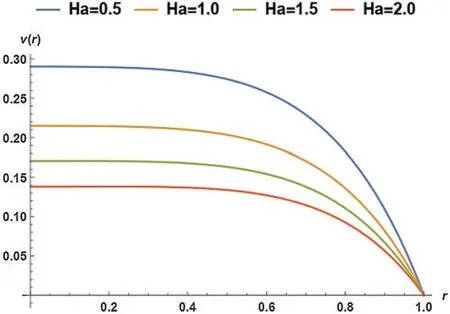
Figure 6:Non-dimensional velocity of the magnetic particles as a function of Ha at G= 0.2

3.6 Non-Dimensional Velocity of the Magnetic Particles as a Function of Ha at G=0.8

In Fig.7,the Hartmann Number effect was studied at four different values; however,the particle mass parameter (G)was kept constant at 0.8.The magnetic particle’s velocity (v)varied at four variousHavalues,but in the end,velocity converged atr=1.The velocity of magnetic particles declined as the Hartmann number increased from 0.5 to 2.0 (with increments of 0.5).

Figure 7:Non-dimensional velocity of the magnetic particles as a function of Ha at G= 0.8

3.7 Non-Dimensional Velocity of the Magnetic Particles as a Function of k at R=0.2

In Fig.8,the effect of an electro-osmotic parameter (k)was studied at four different values;however,the particle concentration parameter (R)was kept at 0.2.Fig.8 trend was sinusoidal except at the curve wherek=5.The figure described the effect of varyingk(from 5 to 20 with increments of 5)on the magnetic particles’velocity.

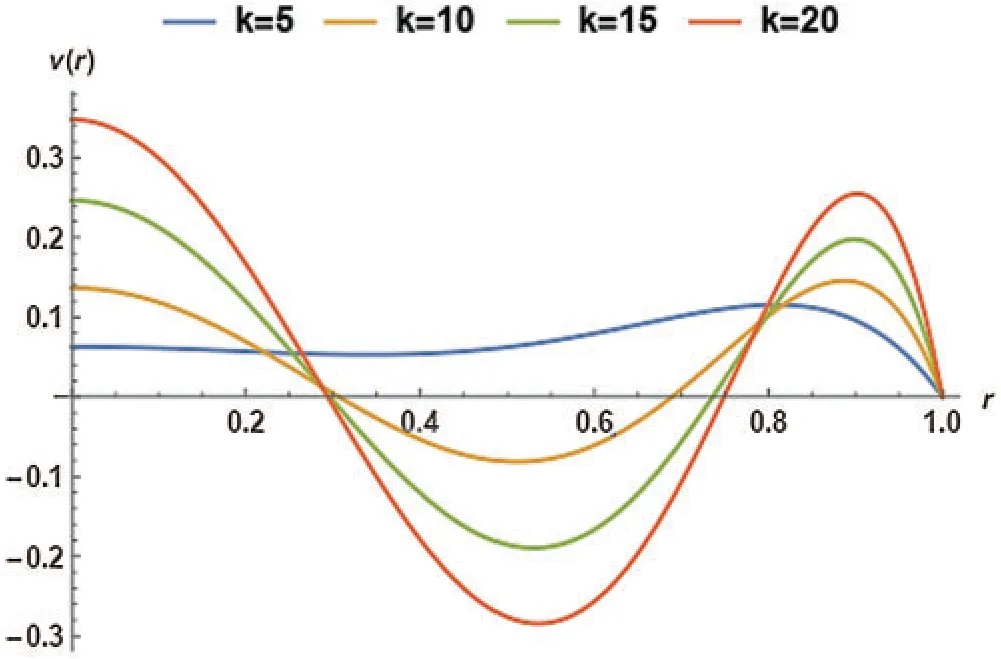
Figure 8:Non-dimensional velocity of the magnetic particles as a function of k at G= 0.2

3.8 Non-Dimensional Velocity of the Magnetic Particles as a Function of k at R=0.8

In Fig.9,the effect of an electro-osmotic parameter (k)was studied at four different values;however,the particle concentration parameter (R)was kept constant at 0.8.Fig.9 trend was sinusoidal except at the curve wherek=5.The figure described the effect of varyingk(from 5 to 20 with increments of 5)on the magnetic particles’non-dimensional velocity.The magnetic particles’non-dimensional velocity changed as sinusoidal at four various values ofk,but in the end,velocity converged atr=1.It can be seen that the velocity declined askrises untilr=0.3,and the final solution converged atr=0.3.Hereafter,the velocity once more dropped then rises up tor=0.8,where the curves converged,rose over with the last drop,and ultimately converged atr=1.

Figure 9:Non-dimensional velocity of the magnetic particles as a function of k at G= 0.8

3.9 Non-Dimensional Velocity of the Blood

The particle mass parameter (G)was chosen as 0.2 or 0.8.The non-dimensional velocity of blood decreased as the Hartmann number increases,i.e.,Ha= 0.0 to 1.5 (with increments of 0.5).The declining value of velocity was owing to two factors specifically:electrical conductivity (σ)and radius of micro-tube (h).Whenhincreased,theHaalso increased,thus increasingHaled to a decrease in the value of velocity,the non-dimensional velocity of the blood.The existence of a Lorentz resistive force opposes the flow of blood during the interaction with a magnetic field,which results in a decline in velocity of the blood with augment inHa.

Whenhincreased,σalso increased due to the presence of EDL at the boundary of the micro-tube,so eventually,velocity also increased.Changing the value ofGfrom 0.2 to 0.8,all the effects were the same as discussed above.It can be seen in Figs.2 and 3.

Selecting particle concentration parameter (R)as 0.2 or 0.8 and changing the value of electroosmotic parameter,i.e.,k= 5 to 20 (with increments of 5),the non-dimensional velocity of the blood exhibited sinusoidal behavior.This sinusoidal behavior was due to the radical relationship of Debye length (EDL thickness).The presence of EDL at the micro-tube circumference gave an increase to a higher bulk ionic concentration (n0)at circumference only.Thus,the sinusoidal curve atk= 10 had a lower value of velocity thank= 20.Atk= 5,the curve converged only atr= 1,therefore,giving the most appropriate result.As the velocity did not decrease,instead,it increased for some values ofr.The results are shown in Figs.4 and 5.

3.10 Non-Dimensional Velocity of the Magnetic Particles

Choosing particle mass parameter (G)as 0.2 or 0.8,the non-dimensional velocity of blood decreased as Hartmann number rises,i.e.,Ha= 0.0 to 1.5 (with increments of 0.5).The declining value of velocity resulted from two factors:electrical conductivity (σ)and micro-tube radius (h).When h increased,the Ha also increased,so increasingHadecreased the non-dimensional velocity of magnetic particles.This is most likely due to increasing the strength of the magnetic field in the micro-tube.Furthermore,as the particle mass parameter(G)is increased,the particle velocity decreases.This decline in the velocity is most probably as a result of the aggregation of the magnetic particles.Whenhincreased,σalso increased due to EDL at the micro-tube boundary,so ultimately,velocity also increased.It can be seen in Figs.6 and 7.

Selecting particle concentration parameter (R)as 0.2 or 0.8 and changing the value of an electro-osmotic parameter,i.e.,k= 5 to 20 (with increments of 5),the non-dimensional velocity of magnetic particles showed sinusoidal behavior.The magnetic particle’s velocity varied as sinusoidal at four variousHavalues,but in the end,velocity converged atr= 1.This sinusoidal behavior was due to the radical relationship of Debye length (EDL thickness).The presence of EDL at the micro-tube circumference contributed to a higher bulk ionic concentration (n0)at circumference only.Thus,the sinusoidal curve atk= 10 had less velocity thank= 20.Atk= 5,the curve converged only atr= 1,therefore,giving the most appropriate result.As the velocity did not decrease,instead,it increased for some values ofr.The results are shown in Figs.8 and 9.

4 Validation

To validate the computational results of the current study,the calculated blood velocity from this study has been compared with the Crank-Nicolson method computing the characteristic of blood flow [16].Table 10 presents the comparison of OHAM calculated results with the Crank-Nicolson values for the blood flow.The OHAM computed the parametric conditions precisely by giving a similar trend along the radius of the micro-tube,as shown in Table 10.It can be seen that OHAM results are in accordance with the Crank-Nicolson results for the blood flow.These computed results demonstrate that the OHAM performs satisfactorily and is valid.Accordingly,the OHAM approach can be used to predict the performance of magnetic drug targeting.

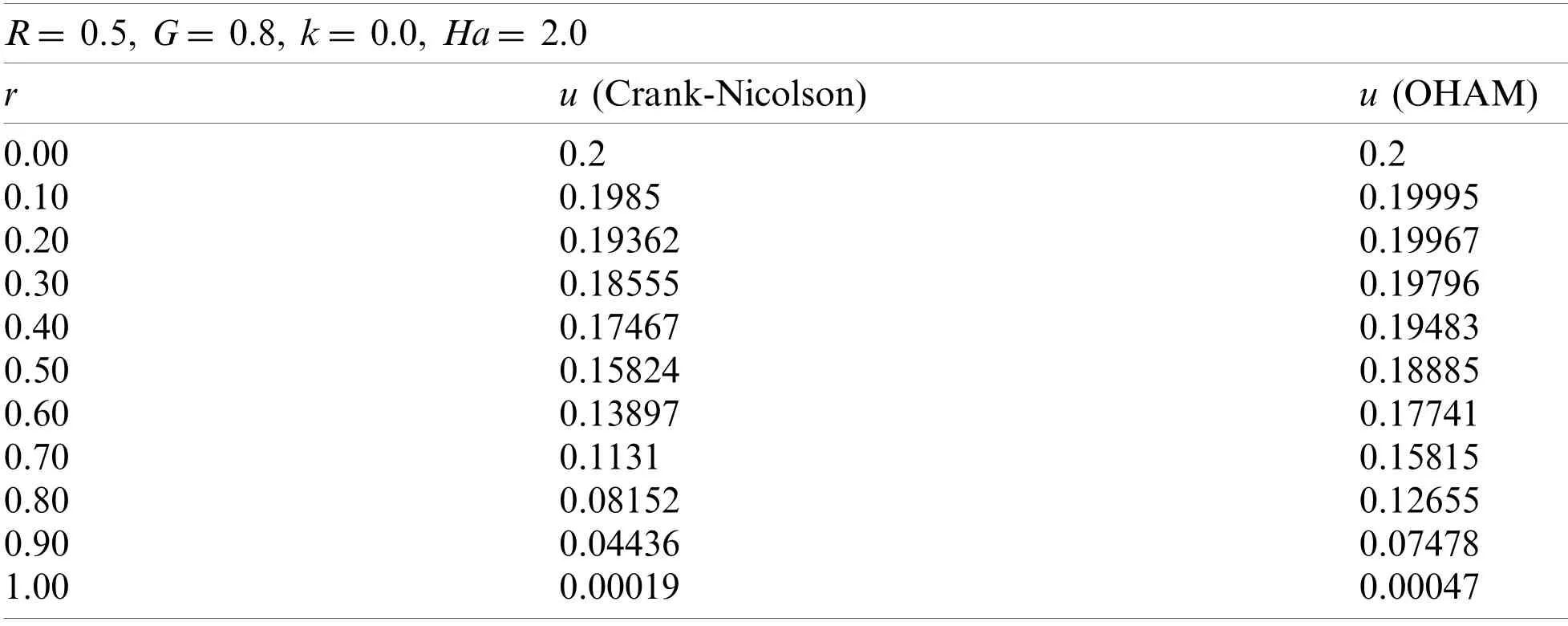
Table 10:Comparison between Crank-Nicolson and OHAM for blood velocity (dimensionless)

5 Conclusion

The present investigation focuses on a theoretical analysis of the blood flow and moment of magnetic nanoparticles inside a cylindrical micro-tube under the influence of both a magnetic field and an electric potential.The Debye-Hückel approximation is used to determine the electroosmotically steered capillary dynamics of blood inside a micro-tube.In this study,we found that the non-dimensional velocity of magnetic particles and non-dimensional velocity of blood may depend upon various constants and parameters like electro-osmotic parameter (k),particle concentration parameter (R),particle mass parameter (G),and Hartmann number (Ha).Using the OHAM approach,the dimensionless form of governing equations was numerically computed and showed rapid convergence.Maximum velocity of magnetic particles is achieved along the center of the micro-tube.The moment of the magnetic particles can be controlled by altering the strength of the axially applied electric field as well as the magnetic field.In order to validate our computed results,we compared them with the relevant data,which revealed reasonable agreement.From this study,we can deduce that the flow of blood and magnetic particles can be substantially enhanced by adjusting the magnitudes of the transverse electric field and the applied magnetic field.It may be deduced that the presence of magnetic nanoparticles in blood fluids could be beneficial in therapeutic solicitations,especially in the case of drug delivery.This analysis of nanofluids reflects the escalation findings in thermal levels by accumulating additional nanoparticles to the primary liquids.It was found that by the levels by accumulating different nanoparticles,the capacity of thermal conduction of the base liquid intensified.Such investigation was also established for the magnetic nanoparticles,as indicated in the results.The greater and intensifying effect of nanoparticles may lead to better drug delivery.

Acknowledgement:The authors would like to acknowledge the University of the Punjab and COMSATS University,Pakistan,for providing the necessary assistance to carry out this research work.The authors are also grateful to Dr.Arif Masud from the University of Illinois,Urbana-Champaign,the United States of America,who provided us with valuable direction during this research work.Furthermore,we would like to appreciate the Super Computing facility at Ghulam Ishaq Khan Institute of Engineering Sciences and Technology,Khyber Pakhtunkhwa,Pakistan.

Funding Statement:This work was supported by the research grant of Jeju National University in 2020,the Basic Science Research Program through the National Research Foundation of Korea (NRF)grant funded by the Korea Government (Ministry of Science and ICT)(NRF-2018R1A4A1025998),and Higher Education Commission of Pakistan (Project No.210-3800/NRPU/R&D/HEC/1530).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.