数字梯度敏感法测量系统的改进及应用

付保飞

摘要：在介绍数字梯度敏感（Digital Gradient Sensing，DGS）方法与数字图像相关（Digital Image Correlation，DIC）方法原理的基础上，将2种方法相结合以扩展数字梯度敏感方法的测量领域，设计提出透明材料的应力梯度场与位移变形场同步测量系统。荧光散斑方案解决散斑靶标与试件表面散斑场的成像冲突问题，3CCD彩色相机方案解决2种散斑场的圖像采集问题，通过开展三点弯曲实验进行数据分析以及精度对比，验证了同步测量系统的可行性与有效性。

关键词：数字梯度敏感方法；视觉测量；光学测量；图像处理；数字图像相关方法

中图分类号：TP391文献标志码：A文章编号：1008-1739（2022）07-52-6

0引言

数字图像相关（Digital Image Correlation，DIC）方法是一种非接触式光测方法，基于物体表面散斑图像灰度对比分析物体变形前后的图像，从而得到整个感兴趣区域的位移变形量。该方法具有测量设备简单、环境要求较低等特殊优势，是目前光测力学领域较为活跃的研究方法。由于DIC方法采用了一阶泰勒级数表示的位移梯度与微分方程表示的噪声位移数据等多种原因，DIC测量在出现应力集中、残余应力和断裂冲击等现象时会表现出低精度的问题[1]，在此背景下，数字梯度敏感（Digital Gradient Sensing，DGS）方法应运而生。

DGS是Tippur等人[1]最早提出的一种基于DIC的非接触式光测力学方法，通过测量透明物体由于应力非均匀分布/非均匀变形导致的光线角偏转得到透明物体变形过程中的应力梯度分布。DGS方法提出后，有效地解决了透明材料在应力集中、冲击断裂等方面的测量精度问题。另外，DGS是在DIC的基础上发展而来，不仅继承了DIC的优点，而且在测量过程中，不需要每次都对试件重复制斑，既节省了时间也保证了试件原有功能，而且得益于DIC方法计算效率[2-3]、测量精度[4-5]以及商用软件的发展，DGS方法在科学研究与工程实践中表现出极大的潜力，在材料缺陷检测、断裂力学、冲击动力学以及高温和高速测量领域均获得成功应用[6-9]。

现阶段对物体变形表征的对象主要是位移应变以及应力梯度。对位移应变场的测量而言，目前的光测方法以DIC最为实用。而DGS目前的测量范围局限在透明材料的应力/应力梯度的测量表征上。由此可知，如何扩展测量领域使DGS方法实现位移应变场与应力梯度场的同步测量在DGS的改进方面具有指导意义，但该方面的研究仍是一片空白。

为了实现透明材料的位移场与应力梯度场的同步测量以扩展DGS的测量领域，本文在对DGS以及DIC的原理阐述后，通过引入荧光散斑与3CCD彩色相机设计了DGS与DIC相结合的同步测量系统；然后，开展基于设计同步测量系统的三点弯曲实验，对测量材料的位移应变场与应力梯度场进行同步测量；最后，将测量结果与理论真值对比分析，以验证同步测量系统的可行性与准确性。

1原理

1.1 DGS基本原理

1.2 DIC的基本原理

DIC使用相机采集试件变形前后图像，通过插值、搜索等算法对变形前后图像进行匹配以获取试件的位移变形场。二维DIC的测量系统如图2所示，包括工业黑白相机、计算机、试件、光源及加载设备。试件处在工业相机的正前方，并且保证其表面与工业相机光轴垂直，通过上位机软件控制相机采集试件在不同载荷下的散斑图像。

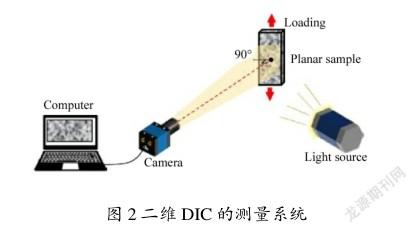
1.3数字图像相关法基本原理

图3展示了DIC的基本原理，在参考图像中选取以计算像素点（0，0）为中心的像素大小为（2+1）（2+1）的区域，将其称为图像子区，在变形图像中按照选定的搜索算法及相关函数进行相关计算，通过不断地搜索及计算找到与参考图像子区相关系数取极值的变形目标图像子区（以（0，0）为中心），参考图像子区的计算像素点（0，0）的位移分量，（对应，方向）便可以确定。选择图像子区而不是单个像素点进行匹配是因为该子区具有更大的灰度变化，能够区别于其他子区，从而在变形图像中能够更独特、更准确地识别。

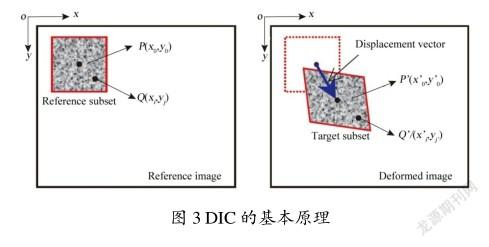
2同步测量系统设计

2.1荧光散斑方案

在DGS测量系统中，相机是工业黑白相机，对透明试件后方的散斑靶标进行成像，从而进行散斑场的分析以获得试件的应力场；在DIC测量系统中，试件表面的散斑场通常通过人工喷涂制备。针对DGS需要对试件后方的散斑靶标成像这一特点，DIC在透明试件上喷涂黑白哑光喷漆这种传统方法会遮挡到后方散斑靶标的成像，因此不再适用。

为了能够实现DIC与DGS的散斑场互不冲突、互不遮挡地成像，提出了采用紫外荧光散斑进行DIC分析以解决此问题，利用荧光颗粒制作随机散斑。荧光散斑由荧光染料作为主要成分喷制而成，荧光染料属于功能性发光染料，与一般染料的区别在于当特定波长外来光（如紫外光）照射时，能吸收一定形态的能量，激发光子以低可见光形式将吸收的能量释放出来，从而产生不同色相的荧光现象。不同色光结合形成鲜艳色彩，当光停止照射后，发光现象消失。

具体方案是使用透明长波紫外荧光染料，喷涂在透明试件表面，在紫外灯照射下会激发出对应颜色的可见光。而DGS系统中的散斑靶标对应另外一种颜色的散斑成像，这样便可以解决散斑场互相冲突的问题。在2种散斑的冲突问题解决后，考虑如何顺利采集到这2种散斑各自的图像信息。

2.2彩色相机方案

对于DIC与DGS以往的系统设置，图像采集设备一般为工业黑白相机，单色成像，无法支撑上一小节提出的荧光散斑方案。于是设计使用彩色相机来解决成像问题，对于彩色相机的成像，本文方案采取三棱镜方式实现的3CCD彩色相机，对于单CCD或CMOS相机，其每个感光像素点都是将光子转化为电子，而电子量的多少反映的是光线的强弱信息，并没有波长信息（颜色信息），因此3CCD彩色相机能够获得彩色图像主要是通过三棱镜将红绿蓝（RGB三基色）分离开，对应每个颜色配置一个CCD进行感光，最后实现彩色成像。

在此基础上，将DIC分析的荧光散斑在激发状态下设置为蓝色，DGS分析的散斑场设置为红色。最终进入到彩色相机中成像，分别对应蓝色通道与红色通道，采集完成后，通过对图像分离可得到各自的散斑场变化。

2.3同步测量系统设置

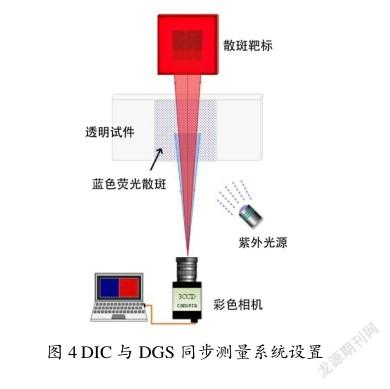
DGS与DIC相结合以进行应力梯度场与位移应变场同时测量，测量系统设置如图4所示，主要由计算机、彩色相机、紫外光源、预制好带有荧光散斑的透明试件以及背光数字散斑靶标组成。值得注意的是，同步测量系统中的散斑靶标不同于目前DGS系统中常用的喷制散斑靶标，其基于背光技术与数值模拟散斑被应用到DGS方法中，可以简化实验装置，提高采集速度并改善散斑质量[6]。

DIC与DGS同步测量系统设置如图4所示，将系统安装完成后，便可以进行测试。图中背光数字散斑靶标发出的是红光进而成像到彩色相机的红色通道；而透明试件表面预制好在紫外光源激发下能够发出蓝光的荧光散斑，从而生成蓝色散斑图像成像到彩色相机的蓝色通道。在图像采集完成后，对彩色相机的两通道进行图像分离操作，分离完成后，分别对两通道中的图像进行DIC与DGS测量分析，最终获得应变位移场与应力场。此同步测量系统将DGS进行了改进，即与DIC系统相结合实现应力场与应变位移场的同步测量。

3实验

3.1实验设置

本节开展三点弯曲实验以验证同步测量系统的有效性与准确性。三点弯曲实验设置如图5所示，包括图像采集系统、背光数字散斑靶标、带有荧光散斑的待测透明试件、万能试验机以及紫外光源。待测试件由铸造PMMA透明板材激光切割而成，其大小为200 mm×30 mm×5.8 mm，且在待測试件的一长边中心位置使用激光贯穿切割一条长为8 mm的水平裂纹，裂纹宽度为500μm，如图5右侧所示，试件表面喷涂紫外光照射下激发蓝光的荧光散斑。

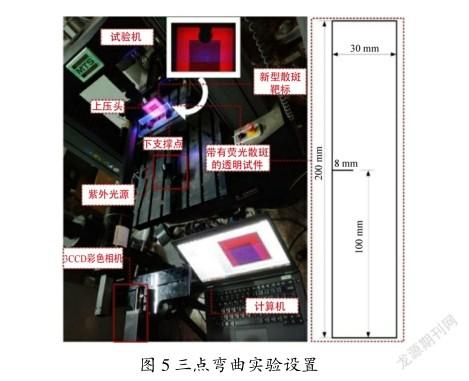
本次实验对带有I型裂纹的试件进行裂纹SIF的测量（对应于DGS分析）以及应变位移场的测量（对应于DIC分析）。首先将选择好的实验装置按照图5所示放置，待测透明试件带有裂纹的一侧长边放在三点弯曲实验装置中的2个支点上；试件与图像采集系统即彩色相机镜头相距=1 500 mm，且与相机光轴保持垂直，在其后侧距离=35 mm的位置平行放置散斑靶标；将透明试件带有荧光散斑的一面朝向相机。

2种散斑场在计算机中清晰成像之后，使用试验机对试件进行加载，实验过程中试件下方的两支点固定不动，上压头对试件中心位置施加载荷，直至断裂；彩色相机分辨率为1628pixel×1 236 pixel×3 pixel（R/G/B），以2 fps的帧率对变形图像进行采集。

3.2三点弯曲实验数据分析与精度对比

3.2.1 DIC分析

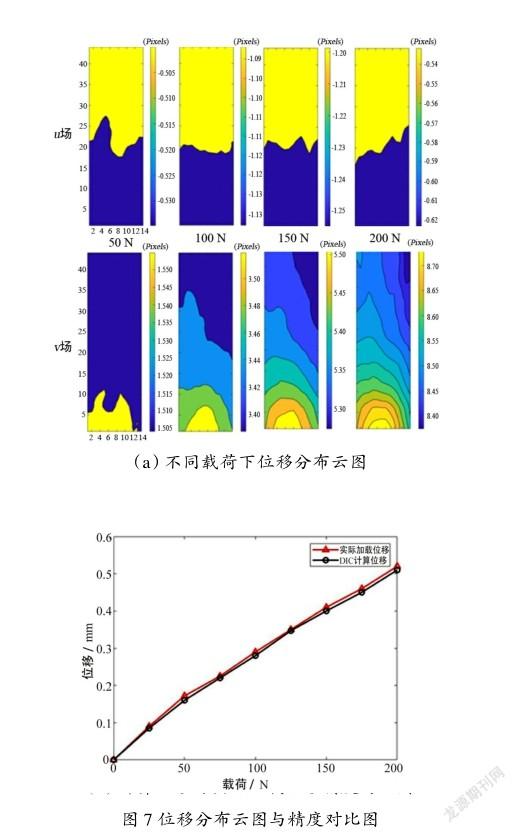
从测量结果可以看出，横向位移场在不同的载荷大小下，变形位移范围都在0.5～1.25 pixel，对应在实际物理尺寸中是非常小的数值，可以忽略不计；着重分析纵向位移场（场），从测量结果中可以看出，随着载荷的不断增加，位移也在不断增大。对ROI区域内场的全场位移求取平均值，然后用比例标尺换算为实际物理尺寸的位移，与试验机压头实际加载位移进行精度对比，对比结果如图7（b）所示。可以看出，本实验方案使用DIC分析所测得的位移与其实际加载位移重合度较高，相对误差控制在5%以内。

3.2.2 DGS分析

通过DGS测量裂纹应力强度因子（SIF），需对采集图像中的红色通道图像进行分析。获得试件变形前后的图像后，通过DIC计算散斑靶标上的散斑图像位移；然后按照推导过程，将计算得出的散斑图像位移与几何关系相结合，得出应力导致的偏转角的变化，得出光线偏转角后，使用计算结果进行后续SIF的计算。

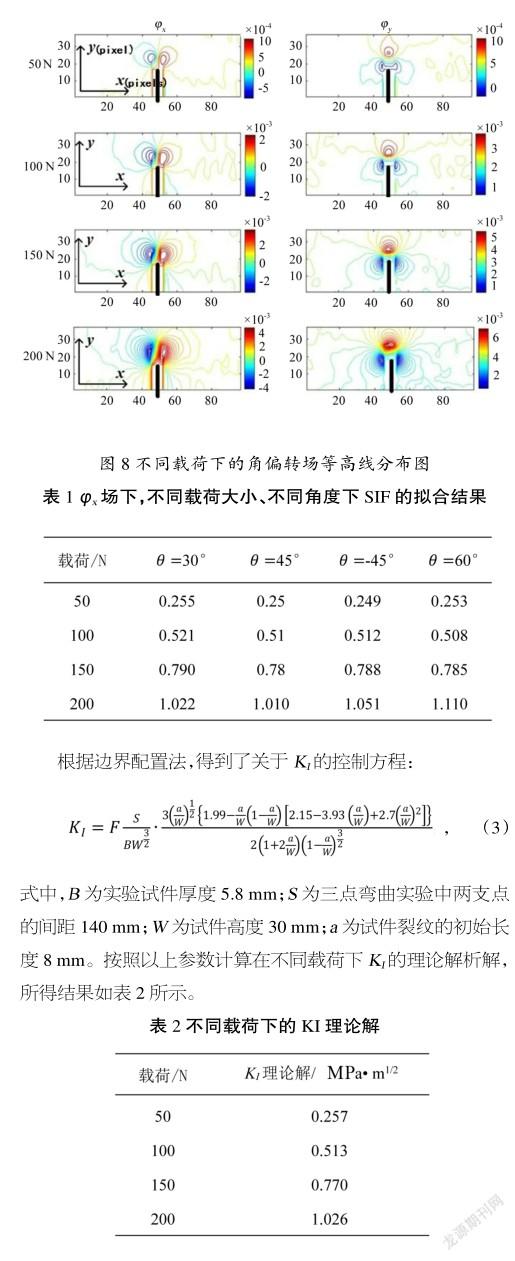
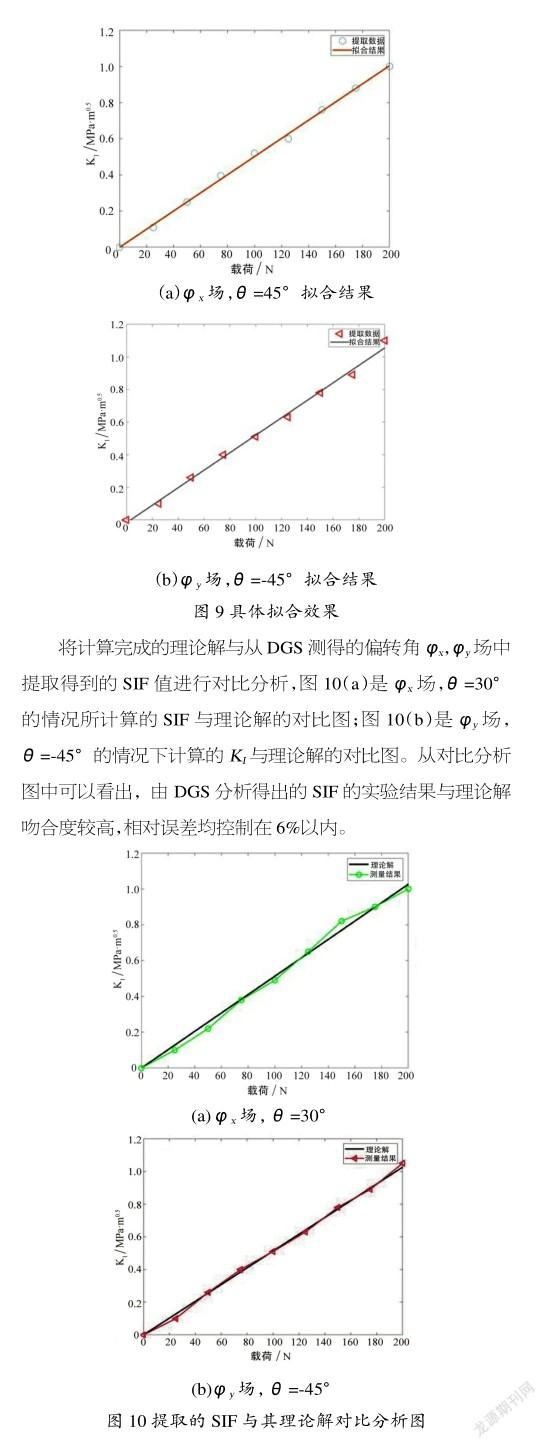
图8展示了不同应力状态下的光线角偏转场等高线图，其中黑色粗实线表示裂纹，可以发现2个方向的偏转角分别呈轴对称分布，且越靠近裂纹附近区域等高线越集中，随着载荷的不断增加，等高线间距在固定的基础上密度不断增大，代表了应力集中程度也越来越大。方向和方向的光线偏转角计算完成后，可利用所得结果进行试件I型裂纹SIF的提取。本节采用了边界配置法[10-11]来进行SIF的计算，此方法有计算过程简单、易于实现的特点，并且是一种针对求解平面裂纹问题的方法。在场下，进行分析提取为30°，±45°，60°，且载荷为为50，100，150，200 N的应力梯度因子的值，最终计算结果如表1所示，随着载荷的不断增大，在几个角度下所提取的SIF值呈现出线性关系，符合脆性材料的变形理论关系。具体拟合效果如图9所示，图中分别展示了在场，=45°；场，=-45°下，载荷与SIF的拟合曲线，可以看出所有数据点都在拟合直线附近，拟合效果良好。

4结束语

本文在介绍DGS与DIC原理的基础上，设计了针对透明材料位移应变场与应力梯度场的同步测量系统。为了验证同步测量系统的有效性及准确性开展三点弯曲实验，通过对实验数据进行DIC与DGS分析，获得了位移场与应力梯度场（偏转角场）。将所获位移场与实际加载位移数据进行对比分析，结果表明位移测量结果误差在5%以内，测量相对准确。对应力梯度场进行SIF的提取，然后将提取值与理论解析解进行对比分析，其6%以内误差的较高吻合度也印证了DGS测量的准确性。

参考文献

[1] PERIASAMY C，TIPPUR H V. Full-field Digital Gradient Sensing Method for Evaluating Stress Gradients in Transparent Solids [J]. Applied Optics， 2012，51（12）2088-2097.

[2] PAN B，LI K，TONG W. Fast， Robust and Accurate Digital Image Correlation Calculation without Redundant Computations [J]. Experimental Mechanics，2013，53（7）： 1277-1289.

[3] PAN B， LI K. A Fast Digital Image Correlation Method for Deformation Measurement [J]. Optics and Lasers in Engineering， 2011，49（7）： 841-847.

[4] PAN B. Bias Error Reduction of Digital Image Correlation Using Gaussian Pre-filtering [J]. Optics and Lasers in Engineering， 2013，51（10）：1161-1167.

[5] PAN B， YU L， WU D， et al. Systematic Errors in Two-dimensional Digital Image Correlation Due to Lens Distortion [J]. Optics and Lasers in Engineering，2013，51（2）： 140-147.

[6] FU B， LI C， DONG B， et al. Enhanced Digital Gradient Sensing Using Backlight Digital Speckle Target [J].Sensors， 2020，20（22）：6557.

[7] PERIASAMY C， TIPPUR H. Measurement of Orthogonal Stress Gradients Due to Impact Load on a Transparent Sheet Using Digital Gradient Sensing Method [J]. Experimental Mechanics， 2013， 53（1）： 97-111.

[8] PERIASAMY C，TIPPUR H V.Measurement of Crack-tip and Punch-tip Transient Deformations and Stress Intensity Factors Using Digital Gradient Sensing Technique[J].Engineering Fracture Mechanics，2013，98：185-199.

[9] PILCH A， MAHAJAN A，CHU T. Measurement of Whole-field Surface Displacements and Strain Using a Genetic Algorithm Based Intelligent Image Correlation Method [J]. Journal of Dynamic Systems Measurement & Control，2004，126（3）：479-488.

[10] BROEK D. Elementary Engineering Fracture Mechanics[M]. Berlin：Springer Science & Business Media，2012.

[11]程靳，趙树山.断裂力学[M].北京：科学出版社，2006.