不同截面EPDM密封圈密封性能仿真分析

曾 鹏，王 坚，张旭辉，朱晨菡

(1.中车时代电动汽车股份有限公司，湖南 株洲 412007；2.长沙中车智驭新能源科技有限公司，长沙 410000)

液冷散热器是电动汽车电机控制器冷却系统中的主要结构。目前形成散热器密封腔的主要方式有钎焊成型、搅拌摩擦焊成型及密封圈加螺钉装配成型等。其中密封圈加螺钉装配成型方式具有结构紧凑、制造简单、拆装方便、成本低廉等特点，已被广泛采用。该方式中的密封圈密封效果直接决定散热器的可靠性，而密封圈密封效果取决于密封圈的截面形状。三元乙丙橡胶(EPDM)具有良好的耐氧性、耐气候老化性、化学稳定性、耐热性及电绝缘性等特性，已经成为密封圈的首选材料，但其不同的截面形状对密封效果有很大的影响。本文针对不同截面形状的EPDM密封圈的密封性能进行仿真分析。

1 EPDM材料模型的建立

橡胶材料在受力过程中具有材料非线性和几何非线性，且具有各向同性或近似同性及体积不可压缩或近似不可压缩的特性，其应变能密度函数()的表征模型有Mooney-Rivlin、Yeoh、Ogden等本构模型。其中Mooney-Rivlin是一个比较经典的模型，用它几乎可以模拟所有橡胶材料的力学行为，尤其适合于描述橡胶材料大约100%拉伸变形或30%压缩变形的情况。

本文采用1阶两参数的Mooney-Rivlin模型：

=(-3)+(-3)

(1)

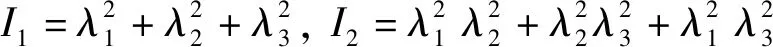
式中：、为与材料相关的常数；、为应变张量不变量；、、为主伸长比。

和是橡胶件仿真分析最重要的两个材料参数，主要是通过橡胶材料试验的方式较精确地获取。最常用的试验方法有单轴拉伸、平面剪切、简单剪切和双轴拉伸。本文采用单轴拉伸对EPDM材料进行测试，试验依据为GB/T 528—2009，测得的EPDM橡胶拉伸力与伸长量数据如图1所示。

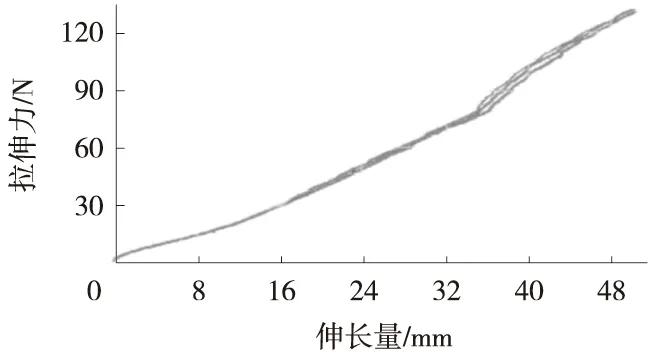
图1 EPDM橡胶拉伸力与伸长量数据

将试验数据中的伸长量转化为应变，拉伸力转化为应力，将曲线上若干点对应的值代入仿真分析软件中的Mooney-Rivlin模型，计算出本文EPDM材料本构模型对应的、参数值分别为0.613、0.719。

2 仿真分析前处理

2.1 密封圈截面建模

橡胶密封圈的边界条件非常复杂，为减少仿真计算量，将三维密封结构简化为平面二维结构。本文密封圈密封形式为端面静密封，设计有通用的Ο形截面密封圈和较复杂的双拱形截面密封圈两种结构。Ο形截面密封圈的直径为2.9 mm；双拱形截面密封圈高度为2.9 mm，宽度为3 mm。

初始状态下，密封圈位于密封槽底部中间位置并与之接触，与密封盖间隙为0.2 mm，即密封圈处于自然无压缩状态。密封圈、密封槽体和密封盖一起组成的密封装配模型如图2所示。

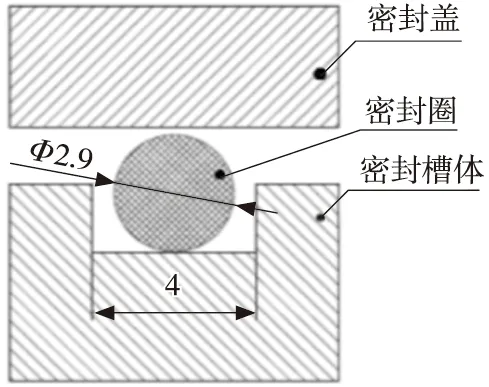
(a) Ο形

2.2 仿真分析条件设定

相比于高弹性大变形的密封圈而言，金属材质的密封槽体和密封盖的变形量很微小，故将密封槽体和密封盖设置为刚体，不考虑其应力和变形。将密封槽体设置为固定全约束，密封盖设置为可沿垂直向下方向移动。

橡胶密封圈与密封槽体、密封盖之间的接触是高度非线性的，属于刚体和柔体间的面与面接触。将密封圈与密封槽及密封盖的相关接触面设置为摩擦接触，摩擦系数0.2；接触算法选择拉格朗日增强算法，接触探测采用Guass Point。

密封圈压缩一定量后，被密封介质流经密封槽体与密封盖之间的间隙与密封圈接触，以流体压力的形式垂直作用于没有与密封槽体、密封盖接触的密封圈面上，故在没有与密封槽体、密封盖接触的密封圈一侧面上施加合适的面压力0.2～0.8 MPa。

密封圈采用四边形单元为主的网格进行划分，单元数量约为15 000，并开启大变形选项。

3 仿真结果与分析

3.1 Von-Mises应力对比

Von-Mises应力反映的是密封圈截面上主应力差值。一般情况下，Von-Mises应力值越大的区域，越容易出现疲劳裂纹，从而密封失效。

无介质压力情况下，密封盖逐步垂直向下移动，当密封圈的压缩率分别为10%、20%、30%时，两种密封圈的应力如图3所示。两种密封圈的最大应力都是随着压缩率的增加而增大，在压缩率为30%时，双拱形密封圈的最大应力小于Ο形密封圈的最大应力。部分应力云图如图4所示。

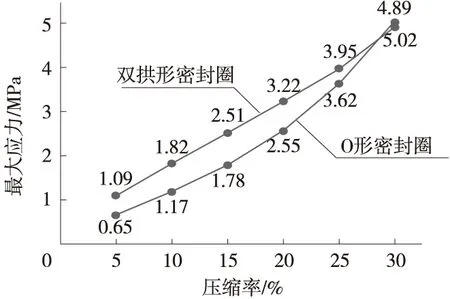
图3 两种密封圈最大应力随压缩率变化图

从图4可以看出，在小压缩率下，Ο形密封圈最大应力出现在接触面附近，随着压缩率增加，Ο形密封圈最大应力点逐步移向截面形状的中心；双拱形密封圈最大应力点则一直位于拱形凸起接触面附近；两种不同截面密封圈的应力分布都是沿截面形状左右、上下对称。

(a) 30%压缩率Ο形截面

3.2 接触压力对比

接触压力是衡量密封圈密封能力的重要指标，接触压力最大值大于密封介质压力值是保证密封圈性能的必要条件。

无介质压力情况下，当密封圈的压缩率分别为10%、20%、30%时，两种密封圈的接触压力分布如图5所示。可以看出，两种密封圈的最大接触压力都随着压缩率的增加而增大，相同压缩率时，双拱形密封圈的最大接触压力均大于Ο形密封圈的最大接触压力。部分接触压力云图如图6所示。

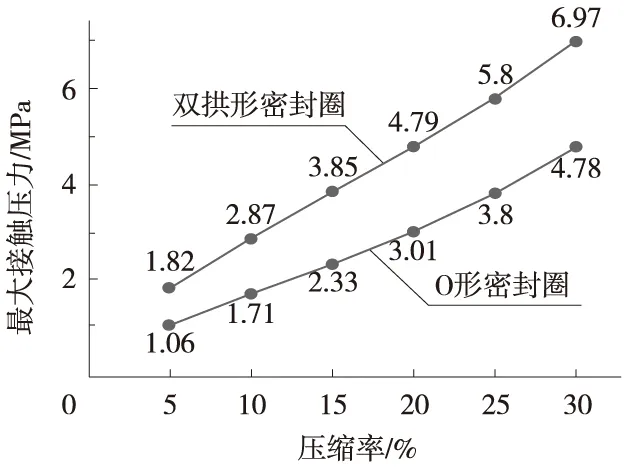
图5 两种密封圈最大接触压力随压缩率变化图

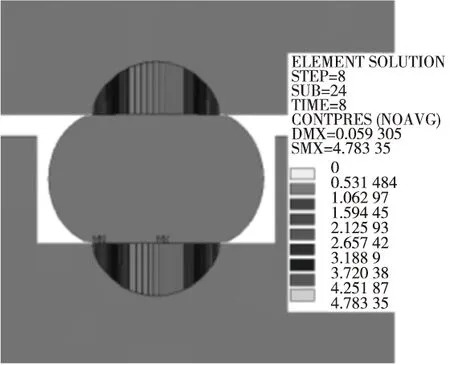
(a) 30%压缩率Ο形截面

从图6可以看出，两种密封圈的整体接触压力分布都是沿截面形状左右、上下对称，每一个接触面的接触压力都呈中间最大、往两侧逐渐减小的状态。

3.3 不同介质压力下最大Von-Mises应力对比

两种密封圈在保持25%、30%压缩率情况下，分别在密封圈一侧施加0.2～0.8 MPa介质压力。其内部最大应力随介质压力变化情况如图7所示。

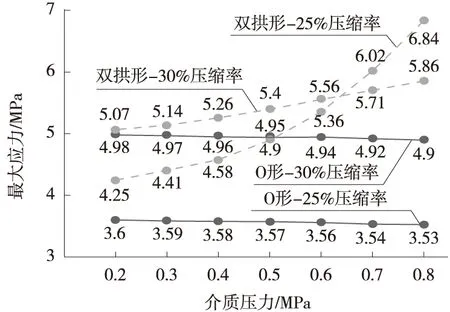
图7 两种密封圈最大应力随介质压力变化图

图中显示，Ο形密封圈内部最大应力随着介质压力的增大而逐步减小，但趋势很弱，原因可能是，介质压力使密封圈大应力区域的面积扩大，应力峰值反而减小；双拱形密封圈内部最大应力则随着介质压力的增大而增大，其中，25%压缩率下最大应力值增大趋势明显，当介质压力小于0.6 MPa时，25%压缩率下最大应力值小于30%压缩率下的最大应力值；而当介质压力大于0.6 MPa时则相反。原因是25%压缩率下双拱形密封圈拱形圆角处在介质压力作用下产生了更大更明显的局部内卷变形，出现了明显的应力集中现象，如图8所示。

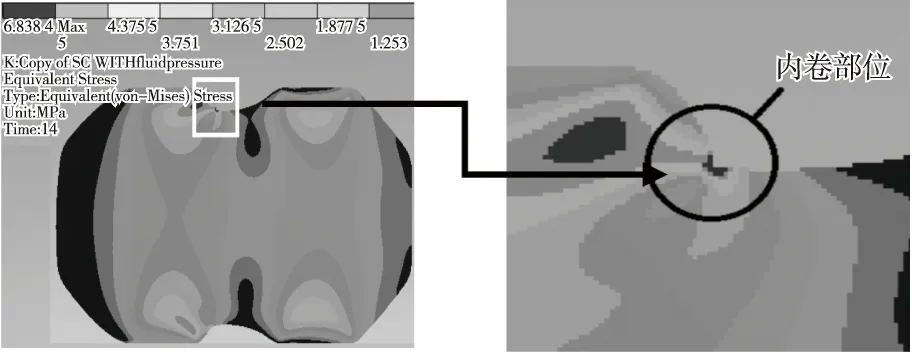
图8 双拱形密封圈内卷变形和应力集中图

3.4 不同介质压力下最大接触压力对比

压缩率及加载与3.3节相同。两种密封圈最大接触压力随介质压力变化情况如图9所示，两者都随着介质压力的增大而增大，且最大接触压力都远大于所对应的介质压力；相同压缩率和相同介质压力时，双拱形密封圈的最大接触压力大于Ο形密封圈的最大接触压力。

图9 两种密封圈最大接触压力随介质压力变化图

3.5 不同压缩率下能密封的最大介质压力对比

密封圈与密封盖、密封槽之间建立起稳定的接触关系，且接触压力大于介质压力才能保证密封圈的密封可靠性，本文以此作为判断密封圈是否失效的依据。通过逐步增大施加在密封圈一侧的介质压力，找出使密封圈与密封盖、密封槽之间的接触关系计算不收敛的临界压力值作为密封圈能密封的最大介质压力值。

当密封圈的压缩率依次为5%～30%(间隔5%)时，给密封圈一侧施加逐步增大的介质压力，得出两种密封圈能密封的最大介质压力及所对应的最大接触压力如图10所示，可以看出压缩率小于20%时，密封圈的最大接触压力都大于能密封的最大介质压力；相同压缩率时，双拱形密封圈能密封的最大介质压力大于Ο形密封圈能密封的最大介质压力。

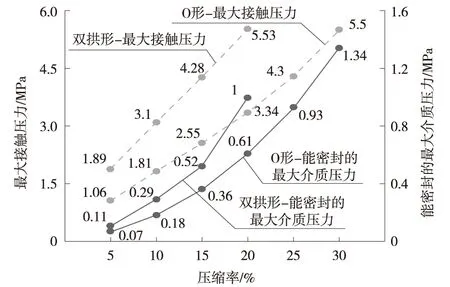
图10 两种密封圈能密封的最大介质压力及对应的最大接触压力随压缩率变化图

图10中，双拱形密封圈在压缩率20%后没有数据的原因如下：当进行压缩率为25%时的最大密封介质压力试验时，双拱形密封圈的最大接触压力和密封圈能密封的最大介质压力都随着所施加的介质压力增大而同步增加，没有最大的稳定收敛状态，故无法得出此压缩率下密封失效所对应的最大介质压力值及最大接触压力值。因此，图10中双拱形密封圈能密封的最大介质压力曲线和对应的最大接触压力曲线就只有到20%压缩率的数据。

4 结束语

1) 通过对两种不同截面密封圈的应力分布、接触压力和能密封的最大介质压力进行对比分析可知，双拱形截面密封圈密封性能优于Ο形截面密封圈。

2) 本文分析未考虑密封盖和密封槽体在介质压力作用下的变形对接触压力的影响，也未考虑介质温度对密封圈材料变形的影响，后续可作进一步研究。