含多分水口的渠道广义积分时滞（ID）控制建模及验证

管光华，朱哲立，王 康

（武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072）

1 研究背景

我国是世界上相对缺水的国家，水资源时空分布不均已成为部分地区经济发展的制约因素［1］。特别是在2013年“一带一路”战略提出后，对沿线地区水资源的支撑能力提出了新的挑战［2］。修建长距离输配水系统，是解决水资源时空分布不均匀和缓解水资源供需矛盾的主要途径之一，对发展灌区农业、保障我国粮食安全、农村社会经济发展和农民增收具有十分重大的意义［3］。但传统依靠人力经验控制的方法会造成大量的输水损失，为此需要采用先进的明渠控制算法进行自动控制［4］。

渠道自动化控制算法一般包括前馈控制和反馈控制。由于水流传播到下游通常需要数小时甚至数天时间，在用水需求发生之前就拟定好沿线闸门的控制规则并提前执行即为前馈控制［5］。反馈控制器与前馈控制器相互独立，根据实时水位偏差进行渠系建筑物的控制。其中PID控制器实际应用最为广泛，但存在参数整定复杂、环境敏感度高等问题［6］。随着技术发展，各种针对多输入、多输出系统的控制算法逐渐应用开来，如线性二次型控制（LQR）［7］、模型预测控制（MPC）［4］、模糊控制［8］、鲁棒控制［9］、神经网络控制［10］等。

控制器的设计一般离不开控制模型。当前使用最为广泛的是荷兰学者Schuurmans在1995年提出的积分时滞模型（ID模型）［11］，并取得了较好的控制效果［4，12-13］。Schuurmans对圣维南方程在初始稳定状态附近进行线性化假设和拉氏变换，将单个渠池概化为时间滞后特性为主的均匀流区和积分特性为主的回水区。ID模型的推导过程中有许多假定和简化处理，其中认为分水口均位于渠池下游尾端［14］。对于欧美发达国家大多数渠道，分水口一般靠近渠池下游，此时分水口的实际分布与ID 模型假设基本吻合。但对于我国灌溉渠道，分水口的布置更为复杂，所受影响因素较多，如地形、种植结构、直灌口门设置、行政区划分、水权管理模式、用水需求新增、历史原因等，实际上沿程分水口的布置可能较为分散。以湖北省漳河灌区总干渠为例，根据实地调研，位于渠池下游尾端的分水口仅占沿线分水口总数的15%左右，若考虑生态取水点，其他位置各规模分水口的总量近百。在控制器设计时，若假定分水口均位于渠池下游端，忽略实际分水扰动对下游控制点水位的滞后影响，势必会对ID 模型的控制效果产生显著影响［15］。当前针对大型输配水工程分水口的研究已开展较多［16-18］，但这些研究均是基于明渠一维非恒定流仿真来分析分水口对渠系水力响应的影响，尚未涉及控制系统建模及控制器的设计。

基于此，本文将对ID 模型深入研究。首先分析分水口位置对ID 模型预测精度的影响，在考虑分水扰动的滞后效应后对该模型进行修正，提出了广义ID模型。分别以传统ID模型和广义ID模型为预测模型，设计模型预测（MPC）控制器，并以美国土木工程师协会（ASCE）经典算例渠池为控制对象进行了渠系自动化控制仿真研究。结果表明，广义ID 模型能够明显改善控制效果，可为类似多输入多输出（MIMO）控制系统的建模提供理论参考，对我国广大灌区输配水系统及大型引调水工程的高效、智能、自动化调度具有较强的实际应用价值。

2 积分时滞（ID）模型

2.1 基本概念 基于对明渠内水波运动的理解，Schuurmans等［11］在1995年提出了一种简化后的控制模型，即Integrator-Delay（ID）模型，见式（1）。该模型将渠池内水面线分为两部分，即均匀流区和回水区，如图1所示，均匀流区水面线与渠底平行，回水区内水流受到下游节制闸的壅水作用而壅高。均匀流区长度的简化计算式见方程（2），若为全回水覆盖情形，Lu=0。ID 模型有两个重要参数：①滞后时间τ，反映水波在均匀流区域的传播时间，s；②回水面积As，反映回水区的水面面积，m2。本文将通过最小二乘法对τ和As进行参数辨识［19］：

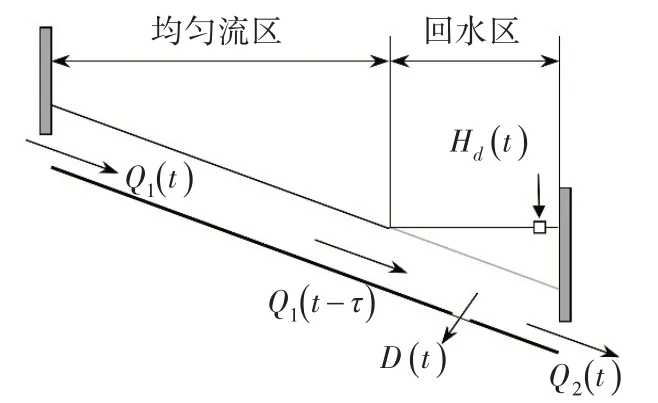
图1 ID模型示意图

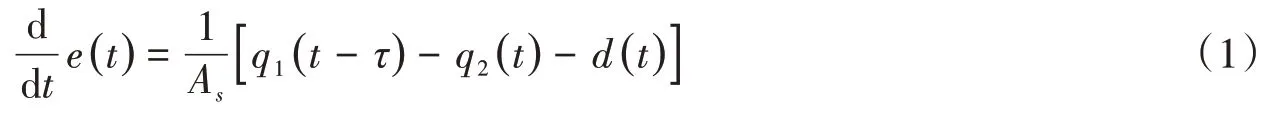
式中：e( )t为t时刻渠池下游水深Hd（t）相对于初始时刻下游水深Hd（0）的增量，m；q1（t-τ）为t-τ时刻渠池入流流量Q1（t-τ）相对于初始时刻入流流量Q1（0）的增量，m3/s；q2（t）表示t时刻渠池出流流量Q2（t）相对于初始时刻出流流量Q2（0）的增量，m3/s；d（t）表示t时刻渠池分水口流量D（t）相对于初始时刻分水口流量D（0）的增量，m3/s：

式中：Lu为均匀流区的估算长度，m；c为重力波波速，m/s；hu为渠池均匀流区平均水深，m；v0为均匀流区平均流速，m/s。

2.2 ID 模型预测精度分析 ID 模型假定分水口均位于渠池下游尾端［14］，但这种假设对ID 模型预测精度的影响尚未见其他学者深入研究。为了探讨ID 模型预测精度与实际分水口位置的具体关系，以ASCE算例2的1号渠池［20］（渠池A）建立仿真模型，基本参数见表1和表2。边界条件设置如下：上游为恒定流量边界；下游为闸门自由出流边界，如表2所示。闸门自由出流公式如下：

式中：Q为闸门自由出流过闸流量，m3/s；μ0为过闸流量系数，仅与闸前水深和闸门开度有关；E为下游闸门开度，m；B为闸门宽度，m；H0为下游闸前水深，m；g为重力加速度，取9．81 m/s2。

渠池A 长7000 m，假设只有一个分水口，可能位于x=0、x=0．5Lu、x=Lu、x=0．5（L+Lu）或x=L等五处（如图2 所示，x为分水口距上游闸门的距离，x=0表示分水口位于上游闸后断面，x=L表示分水口位于下游闸前断面）。T=1 h 时分水口发生阶跃取水工况，取水流量为1 m3/s，观察ID 模型预测结果与非恒定流仿真结果的差异。本文非恒定流仿真在“输水渠道系统运行仿真与控制”软件［21］上进行，该软件使用普莱斯曼四点差分隐格式对圣维南方程进行求解［1］。仿真结果如图3所示。

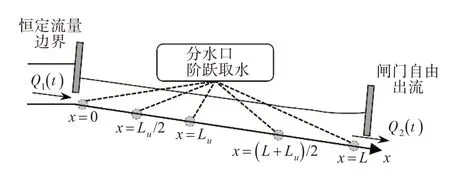
图2 取水口分布示意图

图3 各分水口处ID模型解和非恒定流解的总体标准差

总体标准差值越小，表示模型预测误差越小、预测精度越高。无论分水口位置在哪，ID 模型只有一组预测结果，而非恒定流仿真结果与分水口的实际位置有直接关系，通过对比ID 预测结果和同工况下不同分水口位置的非恒定流仿真结果，计算各分水口位置工况下的总体标准差值，观察ID 模型预测误差的变化趋势。从图中可以看到，对于渠池A 而言，相较于分水口位于渠池最下游端（即下游闸前位置，x=L），ID 模型更适合预测分水口位于均匀流区和回水区交界处（即x=Lu）时的水力响应过程，可将这个位置称为“ID模型最适用的分水口位置”，简称“分水口最适用点”。换言之，ID模型关于分水口的基本假定并不合适。此时，ID 模型预测的不是分水口位于渠池下游端时渠池出、入流增量与下游水位偏差增量的关系，而应该是分水口位于分水口最适用点时渠池出、入流增量与下游水位偏差增量的关系。

从上面结果可以看到，在使用ID 模型设计控制器时，如果假设分水口均位于下游端，会使得ID模型的预测误差较高，进而影响控制器效果。对于渠池A 而言，均匀流区和回水区交界处为其分水口最适用点，对于不同工程的不同渠池，该点位置可能不一样，与具体的工程物理特性、运行工况等多因素相关，但不是本文研究重点。为简化，下述推导过程均假设均匀流区和回水区交界处为ID模型的分水口最适用点。

3 广义ID模型

根据上节分析可知，以ID 模型作为预测模型时，假设分水口位于下游尾端这一做法并不合适。只有当实际分水口恰好位于其最适用点时ID 模型的预测精度才能最高。然而实际工程中，分水口的位置多变，可能位于渠池的任何位置，为此需要对ID 模型进一步修正。由此出发，考虑不同位置分水口相对于其最适用点的分水滞后时间，使得预测模型能够尽可能达到最佳预测效果，本文提出了如下ID修正模型，称为广义ID模型：

式中：i为分水口编号；n为渠池内分水口数量；τ′i为i号分水口相对于最适用点（x=Lu）的分水滞后时间，s；xi为i号分水口距上游闸门距离，m。当分水口位于最适用点上游时，τ′i为正值，表示分水扰动需要一定时间才能对下游水位产生影响；当分水口位于最适用点下游时，τ′i为负值，表示发生分水扰动事件时，广义ID模型能够更快预测下游闸前水位的变化。

为充分验证广义ID模型的先进性，本文设计了三组仿真算例进行研究：第一组，以渠池A 为例，研究在100%和50%设计流量下当分水口位于渠池不同位置时的预测精度（1-1、1-2）；第二组，以渠池A 为例，假设有两个分水口，分别位于渠池上、下游两端，研究同步取水和异步取水工况下的预测精度（2-1、2-2）；第三组，使用多个工程渠池算例进行检验，渠池A 为ASCE 算例2 的1 号渠池（典型小规模、缓坡渠道）（3-1），渠池B为ASCE算例1的2号渠池［20］（典型小规模、陡坡渠道）（3-2），渠池C为南水北调中线工程中的某渠池［7］（典型大规模、缓坡渠道）（3-3）。所用算例能够代表常见明渠输配水工程的渠池类型。算例设计从多角度将广义ID 模型与ID 模型进行对比。各渠池基本参数见表1，ID 模型基本参数及模型验证工况见表2。

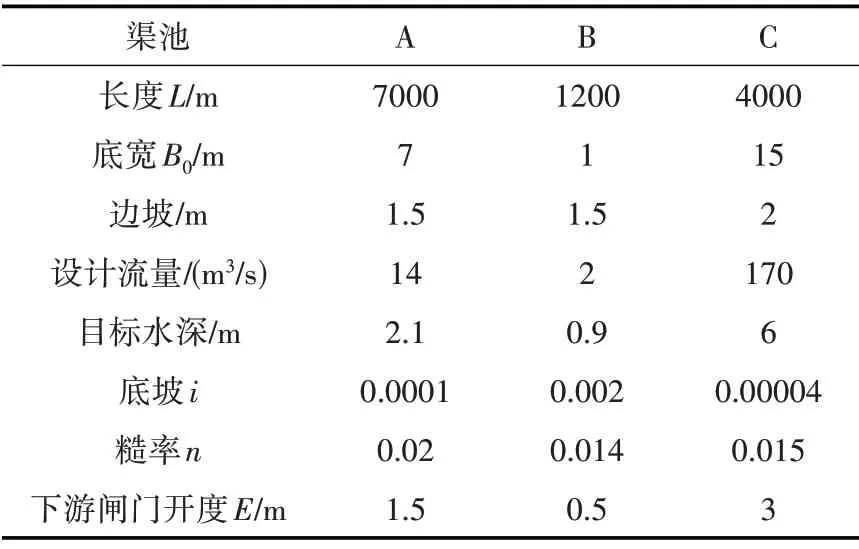
表1 各渠池基本设计参数表

表2 模型验证工况及ID模型参数汇总表

仿真结果如图4—8 所示。图4 和图5 为第一组算例仿真结果，可以看到，对于渠池A，无论在设计流量工况还是小流量工况下，广义ID 模型的预测精度均高于原ID 模型。图6为第二组算例仿真结果，可以看到，同步取水时广义ID模型和ID模型结果相近，分析其原因是，分水口分别位于渠池两端，两分水口滞后影响相互抵消。但在异步取水工况下，广义ID 模型的预测精度明显高于ID 模型。图4、图7和图8为第三组算例仿真结果，观察ID模型的预测误差随分水口位置改变的变化趋势可以看到，渠池A 和渠池B 整体呈“V”字型，即分水口最适用点在x=Lu附近，分水口位置越靠近上、下游两端，ID 模型的预测精度越低；而对于渠池C，整体呈下降趋势，即分水口位置越靠下游，ID模型的预测精度越高，但总体标准差的变化值相较于渠池A和渠池B而言较小，可以初步认为对于渠池C 这类规模极大、坡度极缓的渠道而言，分水口位置对ID 模型预测精度的影响并不大。与前文简化假设（即各算例渠池分水口最适用点均在均匀流区和回水区交界处）并不矛盾。从广义ID 模型的预测效果可以看到，渠池A的改善程度最大，渠池B其次，渠池C最差。从图8中可以看到当分水口位于所取最适用点下游时，广义ID 模型的仿真效果较ID 模型恶化，主要原因在于渠池C 分水口最适用点位置选取的偏差，根据前文分析，若将渠池C 的分水口最适用点改为渠池下游端，则整体预测效果很可能得到一定程度改善。

图4 各分水口处预测模型解与非恒定流解的总体标准差（渠池A，Q=14m3/s）

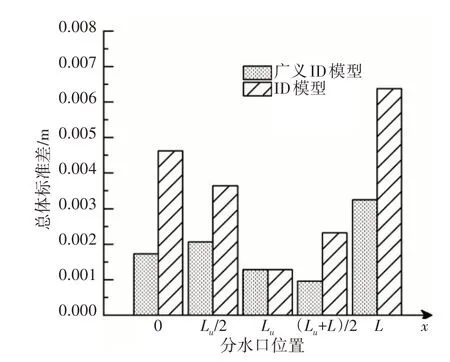
图5 各分水口处预测模型解与非恒定流解的总体标准差（渠池A，Q=7m3/s）

图6 不同取水方式下预测模型解与非恒定流解的总体标准差

图7 各分水口处预测模型解与非恒定流解的总体标准差（渠池B）

图8 各分水口处预测模型解与非恒定流解的总体标准差（渠池C）

由于ID 模型是一个较为简单的概化模型，推导过程中有许多简化和假设，使得分水口最适用点位置难以通过理论推导获得。分水口最适用点位置的选取对广义ID 模型预测精度的改善程度有较大影响，与渠池断面大小、长度、坡度等工程物理特性及运行工况等多因素有关，较为复杂，本文不进行深入分析。但整体而言，当分水口位于渠池上游均匀流区时，相较于ID 模型，本文所提广义ID模型对分水口取水工况的预测精度均得到了一定程度改善。接下来，本文将利用ID 模型和所提广义ID模型作为控制模型设计模型预测（MPC）控制器，进一步检验所提模型的控制效果。

4 模型预测控制算法

4.1 基本方程 将取水计划作为已知扰动项，本文采用下游常水位控制策略和模型预测控制算法（Model Predict Control，MPC）进行控制器设计。MPC使用真实系统的简化模型来进行未来预测，即ID模型或所提广义ID 模型，并通过最小化目标函数J来获得最佳控制动作［4］。本文以单渠池为例，给出控制器的设计过程。首先将控制模型离散化：

式中：k为控制时间步；Ts为模型离散时间间隔，取为1 min；kτ为渠池滞后步数，kτ=τ/Ts；kτ′i为渠池第i号分水扰动滞后时间步数，kτ′i=τ′i/Ts。需要说明的是，当使用ID 模型作为控制模型时，kτ′i= 0。

以此为基础，建立系统的状态空间方程组：

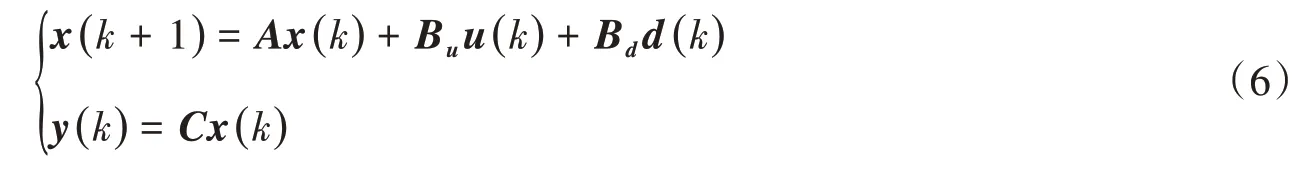
式中：A为系统矩阵；Bu为控制矩阵；Bd为扰动矩阵；C为输出矩阵；y（k）为系统输出向量，包含k时刻水位偏差值e（k）；x（k）为系统状态变量，包含k时刻水位偏差值e（k）及过去kτ时间内的输入量u（k-i），i=1、2、…、kτ；u（k）为k时刻的输入量，即k时刻控制器给上游闸门的动作指令；d（k）为已知分水扰动项。令MPC预测步数为p，控制步数为m，构造如下目标函数：

式中：Q为输出偏差惩罚矩阵，一般令其为单位阵；R为输入变量惩罚矩阵，由于MPC 和LQR 目标函数相似，本文采用钟锞等提出的R矩阵选取方法［7］。这是一个线性二次规划问题，可使用MATLAB的quadprog 函数进行求解。一般将得到的m步最优控制动作序列中的第一步动作发送给上游闸门，在下次调用MPC模块时重复上述模型输出预测和目标函数优化求解等过程。

4.2 控制器参数及控制规则 为充分显示分水扰动滞后的影响，在构建状态空间模型时令Ts=1 min。一般Ts大小与闸门控制时间间隔Tinterval相等，但通常情况下Tinterval≥15 min。为充分利用MPC 的优化结果，令m=1［22］。将一组闸门控制间隔Tinterval和预测时域Tpredict称为一组控制组合，其中Tpredict=p×Ts。控制组合的选取对控制效果影响较大，后文在验证广义ID 模型控制效果的同时，将对控制组合的选取做初步探讨。

为简化，暂不考虑闸门影响（如闸门死区、闸门启闭速度等），上、下游均为流量边界，其中下游以初始流量稳定出流，上游根据控制器指令调整入流。由于当前未考虑闸门死区影响，系统将每隔Tinterval时间调用一次MPC 控制器模块，上游闸门可能持续动作，造成下游水位的持续波动。考虑到渠道输配水系统本身是一个耗散系统，当满足一定条件（如上游来水流量合适、下游水位满足目标水位偏差要求等）时可关闭MPC 模块，减少闸门磨损。当MPC 模块关闭后，令上游来流等于目标流量Qta。在下次计划分水事件发生前至少提前Tpredict时间再重新开启MPC 模块。本文拟定MPC 模块关闭条件如下：

（1）Q∈[Qta-θ,Qta+θ]θ= 0．01；

（2）H∈[Htarget-δ,Htarget+δ]δ= 0．1，即考虑水位死区影响；

式中：Q为上游来流流量，m3/s；Qta为目标流量，等于下游出流与各分水口最终取水流量之和，m3/s；H为下游水深，m；Htarget为下游目标水深，m。

5 仿真结果及分析

5.1 多分水口算例 仍以渠池A 作为仿真算例，假设共三个分水口，位于x=0．1Lu、x=0．5Lu、x=Lu处，在T=3 h时同时阶跃取水1 m3/s。渠池A初始运行流量Q0=11 m3/s，目标流量Qta=14 m3/s。由于τ=13 min，根据τ′i计算式（4），kτ′1=12、kτ′2=7、kτ′3=0。当使用ID模型作为控制模型时，kτ′i=0。

通过控制参数调试，当控制组合为“控制间隔Tinterval=105 min、预测时域Tpredict=135 min”时控制效果较好，仿真结果如图9 和图10 所示，“MPC-ID”和“MPC-广义ID”分别表示以ID 模型和广义ID 模型为控制模型设计的MPC 控制器。从图中可以看到，在预知分水扰动的情况下，模型预测控制算法能够预测未来水力响应，提前操作上游闸门放水补充蓄量，从而降低取水扰动造成的下游水位变幅。仅从仿真结果曲线图难以分辨两种控制模型的优劣，故使用无量纲化水位误差平方积分（NISE）和无量纲化流量误差平方积分（NISQ）等性能指标定量衡量系统下游水位控制及上游闸门流量控制的平稳性，NISE和NISQ值越小，表示水位和流量控制越平稳［23］，计算见式（8）（9），仿真结果如表3所示：

表3 仿真结果表

图9 下游水深变化过程线

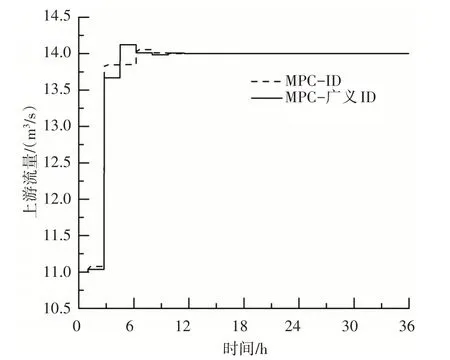
图10 上游流量变化过程线

式中：T为仿真时长，取为36 h；Dt为仿真时间步长，取1 min；yt为t时刻下游水位，m；ytarget为下游目标水位，m；Qt为t时刻上游闸门过闸流量，m3/s；Qdesign为渠道设计流量，m3/s。

由表3 可知，以广义ID 模型为控制模型设计的MPC 控制器，相较于ID 模型，在水位控制平稳性和流量控制平稳性上均有一定程度提高。当前控制参数组合下，在NISE上的改善程度可达43．9%，而在NISQ上的改善程度只有7．4%，对水位控制平稳性的提高远大于流量控制平稳性。需要说明的是，水位控制平稳性和流量控制平稳性存在一定的矛盾，若想渠池下游水位控制更加平稳、精确，上游闸门的动作则需要更加频繁，造成的入流波动就更大。由于ID 模型的直接预测对象为下游水位偏差，而对闸门过流的影响是间接性的，故以NISE为下文控制组合选取的主要判断指标更加合适。

对该组结果进行分析，ID模型认为分水口位于下游端（其实在上游某处）而不考虑分水扰动的滞后，分水事件直接导致下游水位较大波动，此时控制器为保持水位稳定而频繁调节上游闸门；广义ID模型考虑了分水扰动滞后，分水的影响传递到下游时已经由于能量损失相对削弱了很多，所以控制器对上游闸门的调节也相对缓和，下游水位波动更加平稳，故性能指标NISE和NISQ均一定程度降低。

5.2 控制组合选取 控制组合的选取对控制效果的影响较大，一般需要通过试算进行参数调试。为进一步研究不同控制组合下ID模型和广义ID模型的控制效果，进行了如下仿真实验。控制间隔Tinterval=15、30、45、…、180 min，共12种方案；预测时域Tpredict=15、30、45、…、180 min，共12种方案。根据经验Tpredict≥Tinterval，故共需进行78×2=156 组控制组合的仿真试验，仿真结果如图11 和图12 所示。图中1/NISE值越大代表控制效果越好；当Tpredict＜Tinterval时，令1/NISE=0。

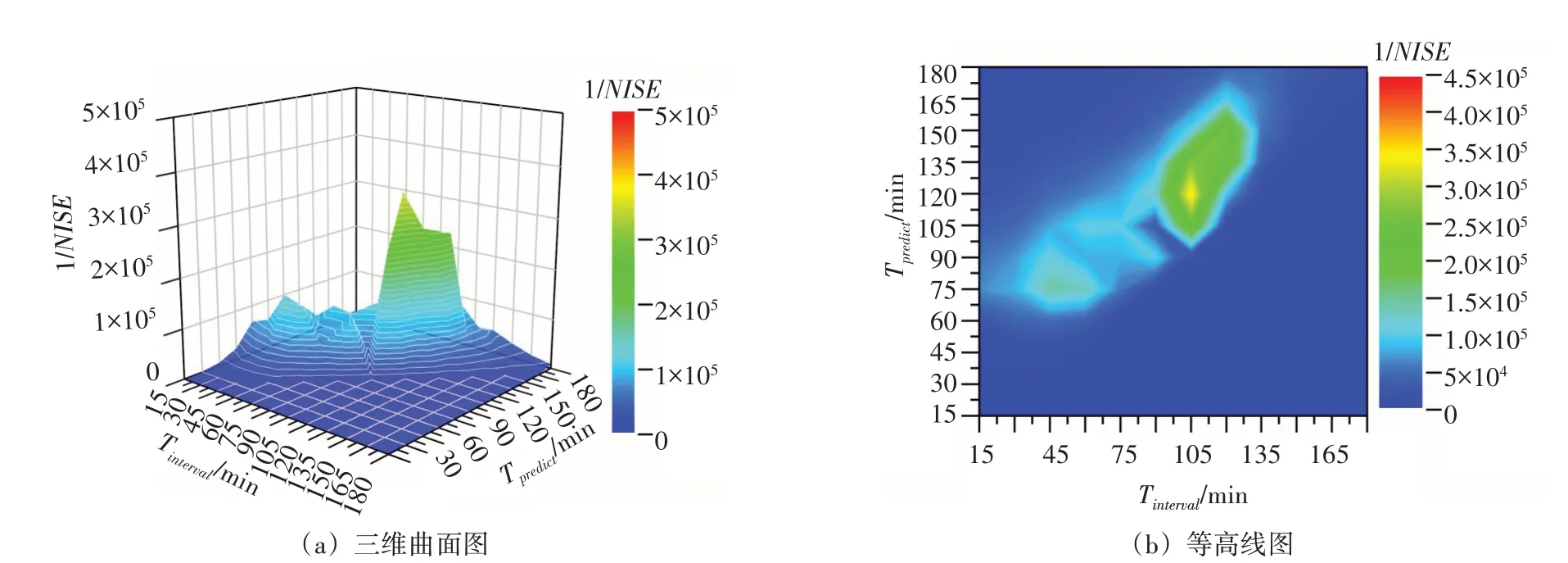
图11 各控制组合下MPC-ID控制效果

两种控制器的最优控制组合并不一样，但从图11（a）和图12（a）中可以看到，在各自最优控制组合下，广义ID模型的控制效果明显好于ID模型。

如何选取合适的控制组合以达到比较好的控制效果对控制器的设计至关重要，一般需要通过不断试错进行参数调试，十分费时、费力。图11（b）和图12（b）中绿色包围区域为控制效果较好的区域，当选取此区域内的控制参数组合时，控制效果可能不是最优，但处于可接受水平。经统计图11（b）中绿色区域约占10．3%，图12（b）中绿色区域约占24．5%。从结果可以看到，当以广义ID 模型为控制模型时，绿色包围区域增大1．38 倍，这意味着在参数调试过程中更容易选取到合适的控制组合，极大程度降低了试错工作量、提高了工作效率。

为比较各控制组合下广义ID 模型控制效果相对于ID 模型的改善程度，给出衡量指标φ，见方程（10）。相应计算结果如图13所示：

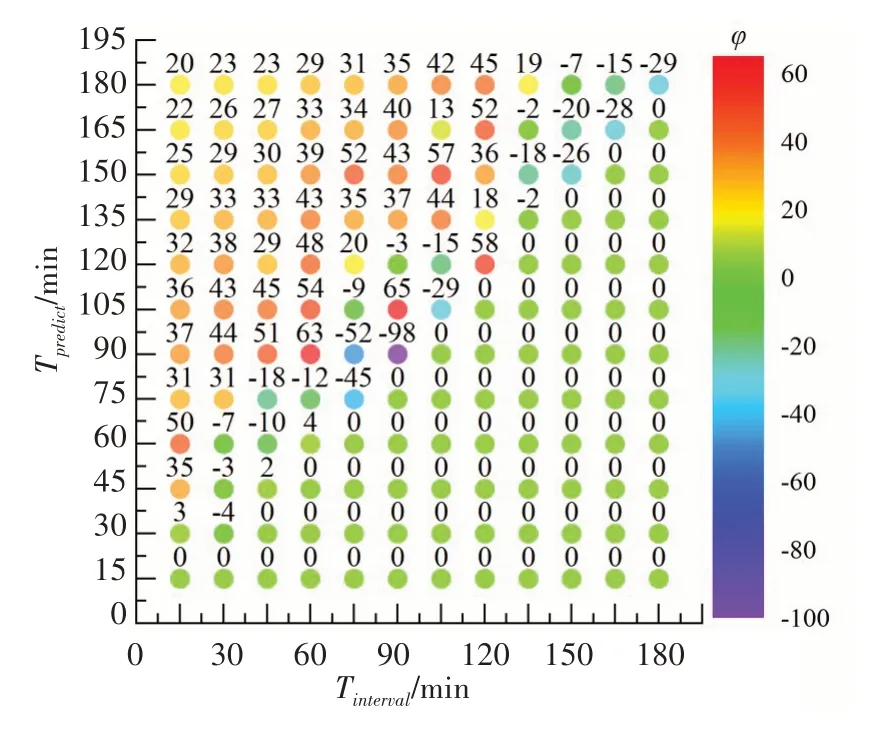
图13 各控制组合下广义ID模型控制效果的改善程度

从图13中可以看到，在合适的控制组合下，如“Tinterval=90 min、预测时域Tpredict=105 min”时，广义ID模型对控制效果的改善程度可达65%。但在部分控制组合情况下，广义ID模型的控制效果比ID模型差。分析其原因在于，ID 模型本身是一个较为简化的线性模型，在此基础上提出假设并进行修正，若控制组合不适合，其误差可能会更大，由此导致了广义ID 模型控制效果的恶化。但从整体结果来看，控制效果得到改善的控制组合数（占71．43%）明显大于恶化的组合数（占25．87%），这从另一角度说明了广义ID模型相较于ID模型更加适合控制器的设计。

6 结论

本文在研究分水口位置对ID 模型预测精度的影响后，考虑分水扰动的滞后时间，提出了广义ID模型。分别以ID 模型和所提模型为控制模型设计MPC 控制器，并以美国土木工程师协会（ASCE）经典算例渠池为控制对象进行了仿真试验，主要结论如下：

（1）提出了适用于多分水口组合的广义ID 模型，经验证其预测精度较传统ID 模型更高。传统的ID 模型假定分水口均位于渠池下游尾端，与我国灌区渠系实际情况严重不符。在分析分水口位置对ID 模型预测精度的影响后，提出了分水口最适用点的概念。考虑实际分水口位置相对于最适用点的滞后时间，提出了广义ID模型。结果表明，对于位于渠池上游均匀流区的分水口，广义ID模型在不同运行流量、不同工程渠池或多分水口取水工况下均有更高的预测精度。

（2）所提广义ID 模型在应用于MPC 控制算法时，较传统ID 模型具有更好的综合控制性能。在合适的控制器参数组合下，水位控制平稳性的改善程度可达65%。

（3）广义ID模型可降低控制参数的试错成本、提高参数寻优速度，更好地满足了MPC算法在线优化实时性的要求。一个较好的控制器需要预测精度较高的控制模型及合适的控制器参数。而控制器参数一般需要通过试错调试，较为费时、费力。当以广义ID模型为控制模型设计MPC控制器时，控制器参数的可选取域增大约1．4倍，意味着调试过程中更容易选取到合适的控制参数组合，提高了寻优效率。

相较于ID模型，本文所提广义ID模型能够考虑不同位置分水扰动的滞后效应，构造更加精细的状态空间方程，对于各先进控制器的设计（如MPC、LQR、自适应控制、鲁棒控制等）均有一定借鉴意义。本文研究对ID 模型进行了初步改进，在分水口最适用点位置以及控制器参数数值求解方法上有待进一步研究。