农村户用光伏储能容量配置研究

杨力人，杨 迪，陈 旭，郑 鹏

（1.西北工业大学，陕西 西安 710072；2.中国三峡新能源集团有限公司甘肃分公司，甘肃 兰州 730070）

国家能源局、农业农村部、乡村振兴局发布的《加快农村能源转型发展助力乡村振兴的实施意见》指出，2025 年将建成一批农村能源绿色低碳试点，利用农村闲置土地、屋顶，建设光伏、风电，配置一定比例储能。《能源发展“十四五”规划》指出，预计我国每年光伏装机容量达50～60 GW，光伏项目须配置10%～20%储能，容量时长2 h[1]。

光伏发电量的精准预测是光伏系统的重要环节，文献[2]建立了粒子群优化预测模型，提高了预测模型的收敛速度。文献[3]提出基于天气预报的聚类再回归预测方法，该方法输入量少、方法简单，且预测精度较高。

电力负荷受天气、节假日等因素影响存在随机性和波动性，对其实现准确、科学的预测，能使发电侧与用户侧达到动态平衡。文献[4]提出基于聚类与自适应划分的短期负荷预测，利用改进的ORELM 模型实现四季负荷多分段建模与预测，预测精度较高。

国家能源局最新发布，截至2020年底我国新型储能规模为3.27 GW，2025 年将超30 GW。储能具有平抑波动、提高电能质量、保障重要负荷供电等作用，该文针对如何使储能配置最优化、延长其使用寿命的问题展开研究，具有一定的指导作用。

1 户用光伏发电预测

1.1 研究对象

研究以在陕西省咸阳市彩虹光伏电站为平台，采用2015～2021年历史数据及对应时间序列的气象数据展开研究。

该电站处于北纬34.32°，东经108.66°，安装在厂房屋顶，容量为30 kWp。光伏组件型号为YL245p29b，采用固定倾角35°、正南方向安装。系统由光伏并网汇流箱、三相30 kW 并网逆变器、交流并网计量柜，以及数据处理及显示系统等组成。

1.2 研究过程

1.2.1 数据处理

为避免离群值对预测精度的影响，选择辐射量完成远离样本主体值的剔除，得到有效数据为2172天，日发电量变化如图2所示。

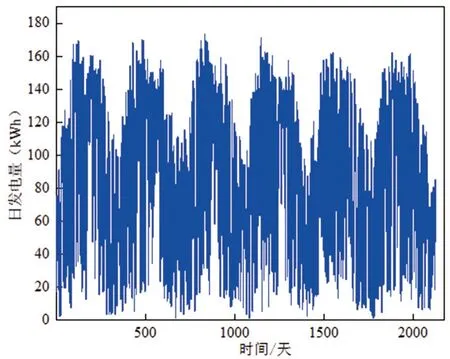
图2 日发电曲线

1.2.2 天气聚类分析

将有效数据按照电站记录的天气进行聚类划分整理，如图3所示。

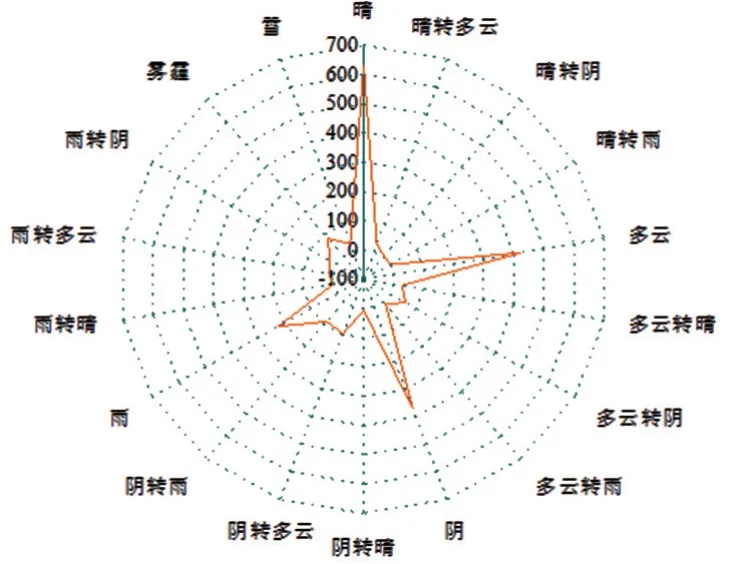
图3 天气类型统计

当分类过多时，须大量样本数据，分类数过少时，预测精度较低。由于样本数据有限，对数据进行初次四季划分，再对天气类型二次划分，如图4所示。

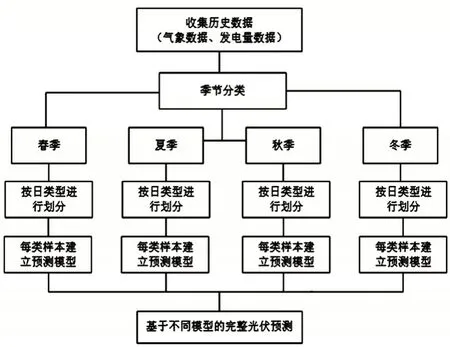
图4 预测模型结构图

1.2.3 灰色关联分析

光伏发电与气象因素有一定的相关性，选择太阳辐射、温度、相对湿度等10个气象因素，通过灰色关联分析进行降维筛选输入量。步骤如下。

确定参考序列X0及比较序列Xi

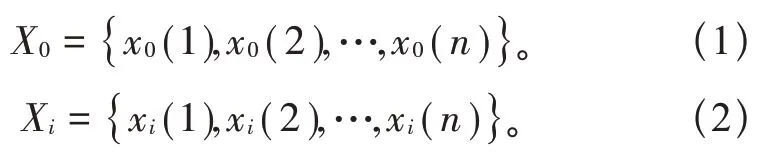
无量纲化处理，采用均值化法，即

以春季晴天为例，其灰色关联度如图5所示。

图5 灰色关联度

结果表明，各气象因素与光伏发电量的关联度均大于0.6，选择大于0.8 的7 个气象因素作为输入量。输出量为日发电量，隐含层节点数的采用经验公式与试凑法。

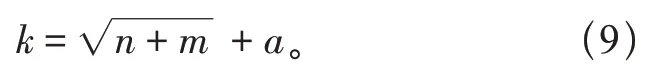
式中：m、n为输入及输出量；k为隐含层节点数；a为1～10之间的常数。

1.3 研究方法

人工神经网络是光伏发电量预测中最有效地预测方法。目前改进的群智能优化算法有遗传算法、粒子群算法等。

粒子群优化模型（PSO）用位置、速度及适应度来表征粒子属性，通过跟踪个体及群体最佳位置得到BP网络最佳的初始化权值及偏差值，达到优化的目的。

该研究采用麻雀搜索算法（sparrow search algorithm，SSA）优化BP 预测模型的权重及偏差值。SSA 依据麻雀觅食行为及反捕食行为提出的一种群体优化算法，具有搜索能力强且调节参数少的优点。其流程图如图6所示。

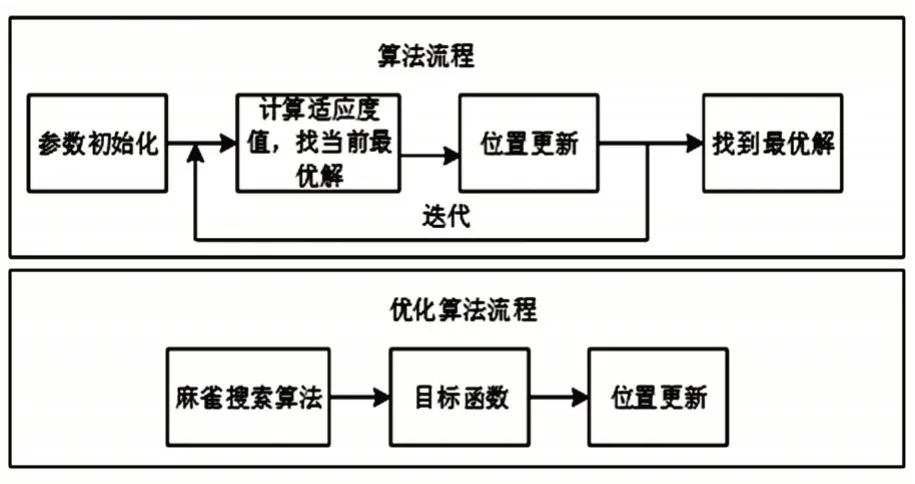
图6 麻雀优化模型流程图

其中发现者位置更新如式（10）所示：

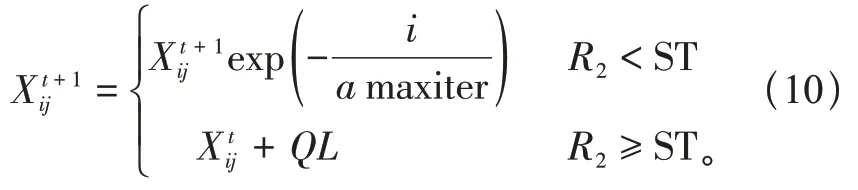
式中：Xij为第i只麻雀在第j维中的位置；t为迭代次数；maxiter 为最大迭代次数α∈( 0,1 ]的随机数，Q为服从正态分布的随机数；L为1×d的矩阵，矩阵内全部元素均为1；R2∈[ 0,1 ]为预警值；ST ∈[ 0 .5,1]为安全值。

加入者位置更新如式（11）所示。

式中：Xp为当前发现者搜索到的最优位置；Xworst为全局最差的位置；A为1×d的矩阵，元素随机赋值为1或-1。

预警者位置更新如式（12）所示。

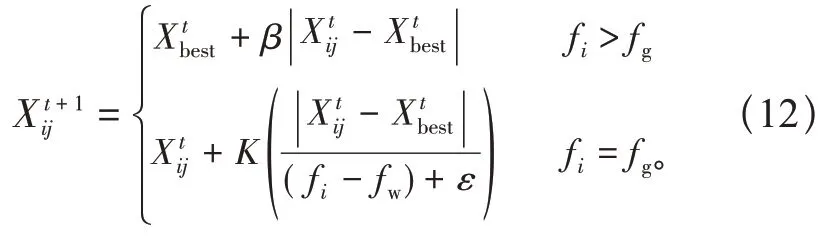
式中：Xbest为当前的全局最优位置；β为步长控制参数，值为服从均值为0，方差为1 的正态分布随机数；K为[ - 1,1 ]之间的随机数；fi为第i只麻雀的适应度值；fg为当前全局最优适应度值；fw为当前全局最差适应度值。

该研究中，种群数为20，SSA - BP 安全值0.8，发现者20%，发现危险的麻雀10%。

1.4 结果及分析

该文以春季为例，对晴、阴、雨3 种类型样本进行预测。晴、阴、雨分别有200、196 及150 组数据，春季晴天的预测结果如图7所示。

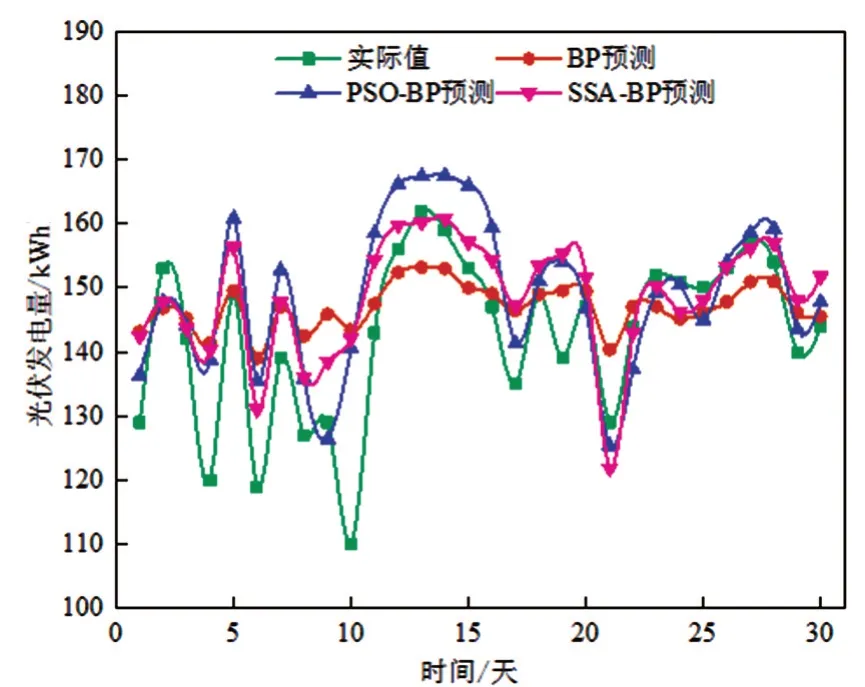
图7 春季晴天预测结果

春季阴天、雨天的光伏发电量预测过程与春季晴天类似，预测结果如图8、图9所示。

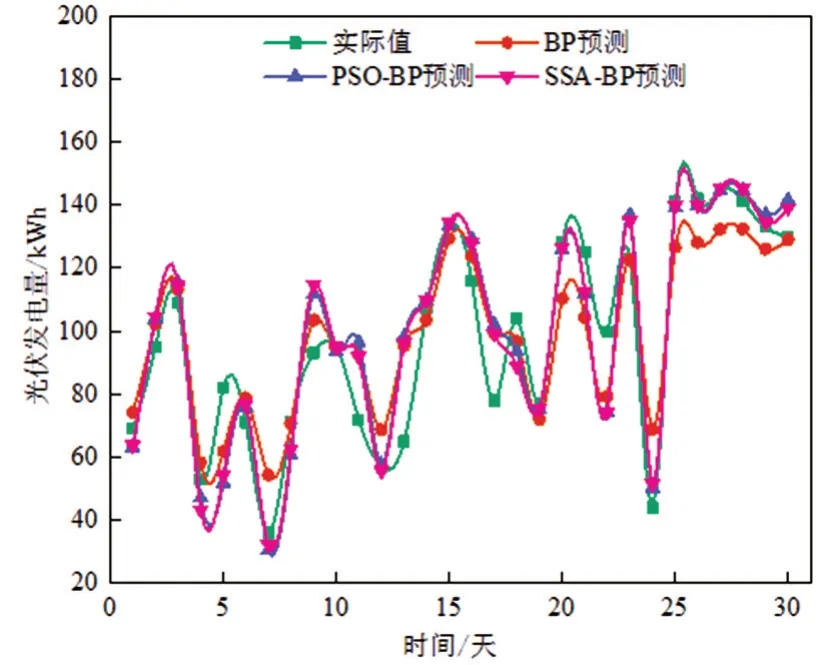
图8 春季阴天预测结

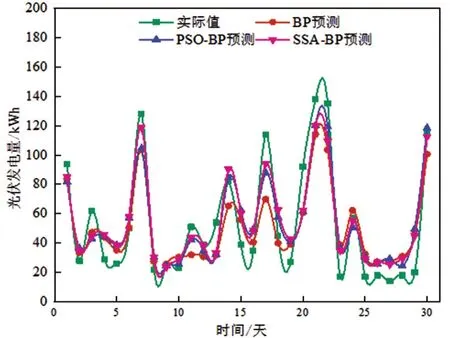
图9 春季雨天预测结果

预测结果表明，晴天的预测精度较高，而雨天、晴天等复杂天气的预测误差较大，通过比较各评价指标，优化后的算法比BP算法性能更好，麻雀优化算法比粒子群优化算法预测误差更小。

2 户用负荷预测

2.1 研究对象

该文以咸阳彬县城关镇330 kV变电站为研究对象，变电站数据包含功率、电压、电流等参数，该文采用2019年1月—2020年9月负荷数据。

图10 变电站实物图

2.2 研究过程

经过数据处理，得到间隔1 h，共14976 组数据。以4号变电站为例，负荷变化如图11所示。

图1 光伏电站

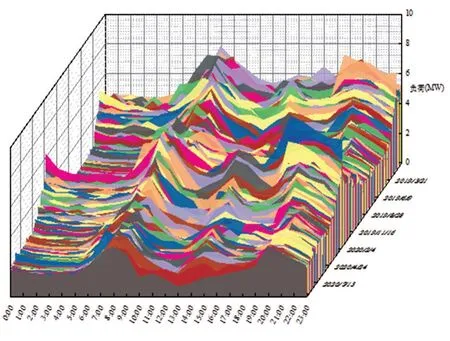
图11 4号变电站负荷数据

2.2.1 灰色关联度

选择温度、湿度、风速等影响因素作为灰色关联度的比较序列，实际负荷值为参考序列，各影响因素与负荷的关联度如表2所示。

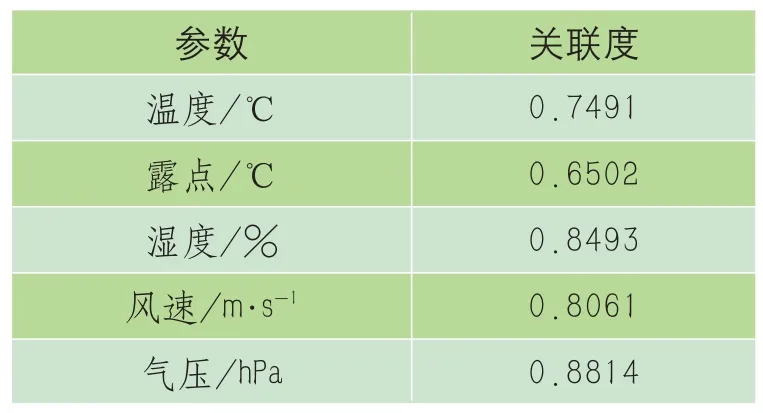
表2 灰色关联度值

结果表明，各影响因素与负荷的关联度均大于0.6，具有一定的关联性。该文选择温度、湿度、风速、气压作为预测模型的输入量。

2.2.2 预测模型建立及设置

LSTM是一种特殊的递归神经网络（RNN），可解决长序列训练过程中的梯度消失、梯度爆炸等问题，能在更长的序列中有更好地表现。

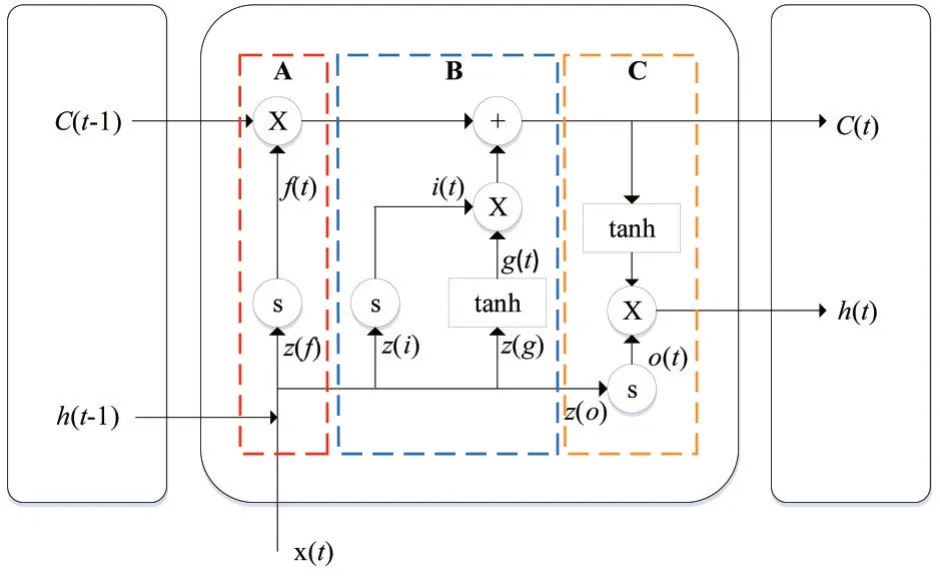
图12 LSTM结构

Sigmoid 激活函数输出区间为(0,1)，可及时更新数据，tanh 与sigmoid 函数类似，但其输出区间(-1,1)。

A：当前输入x(t)与上一时刻输出h(t-1)经过激活函数得到f(t)，该部分负责历史状态单元c(t-1)中的信息传递到当前时刻的部分。

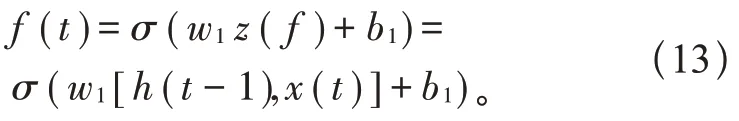
B：输入z(i)经激活函数与g(t)做点积，控制遗留在当前状态单元c(t)中的信息。

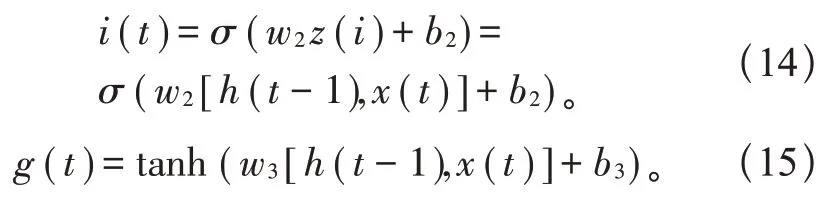
C：控制当前状态单元c(t)到当前输出h(t)中的信息。

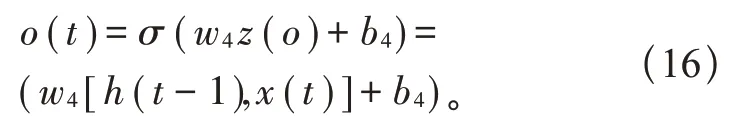
当前状态单元

当前时刻输出

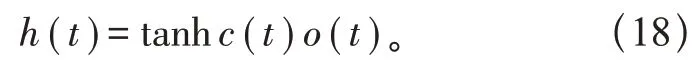
负荷预测的评价指标选择平均绝对误差（MAE）、均方根误差（RMSE）、平均绝对百分误差（MAPE）及逐点偏差率（E），偏差率为

2.3 结果及分析

该文对11 个变电站的总负荷进行不同时间尺度预测，变化趋势与预测结果如图13、图14、图15所示。

图13 24h预测对比及偏差率

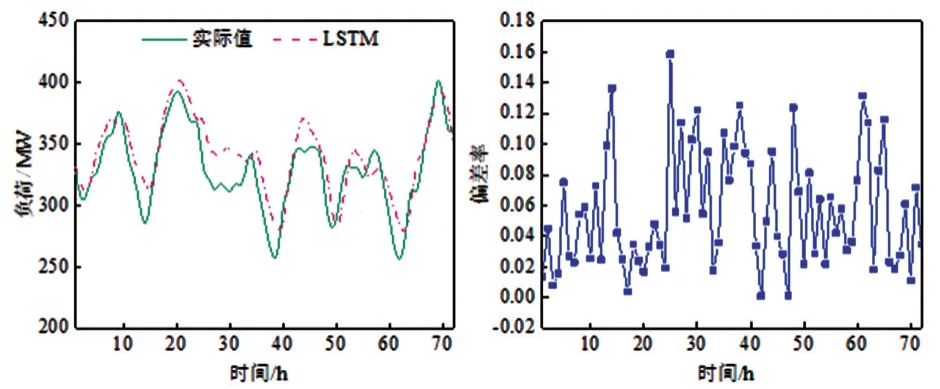
图14 72预测对比及偏差率

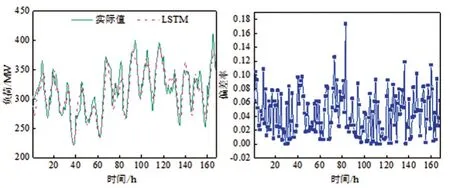
图15 168 h预测对比及偏差率

结果表明，168 h 的预测精度较高，3 种时间尺度的平均MAE、RMSE、MAPE 分别为16 MW、19 MW、5%，平均偏差率几乎在0.14以下。上述研究是电力部门及时协调其他机组以及保证负荷稳定运行的有力支撑。

3 储能容量配置

图16 为负荷功率与光伏出力差值的变化曲线，其中A、B 表示负荷需求量大于光伏发电量，此时需储能或电网为负荷提供电能，C 表示光伏发电量大于负荷需求量，剩余电能须储存起来。该文通过未来72 h、168 h的预测值来验证选择的储能容量实际值是否实现光伏本地消纳最大化，蓄电池选择2 V/800 Ah铅晶电池。

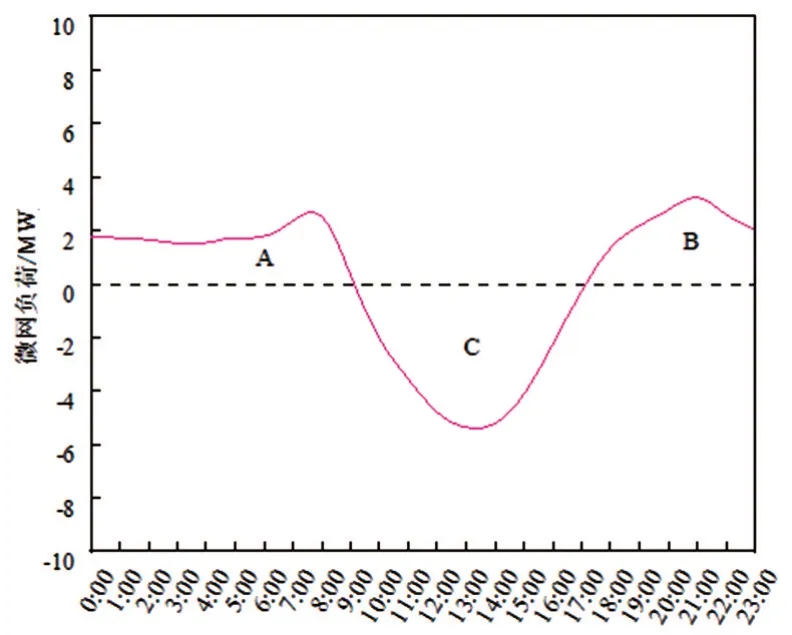
图16 负荷功率与光伏出力差值的变化曲线

微网系统在运行过程中能量变化类型有8 种，如图17所示。

图17 储能优化流程图

其中：m为蓄电池额定容量；n为蓄电池可用容量（nmax=0.7m）；f、k为从电网调用及输送至电网的电量。

3.1 配置方案

3.1.1 典型日储能配置

该文典型日选择春分、夏至、秋分及冬至，负荷功率与光伏出力差值的变化曲线如图18所示。

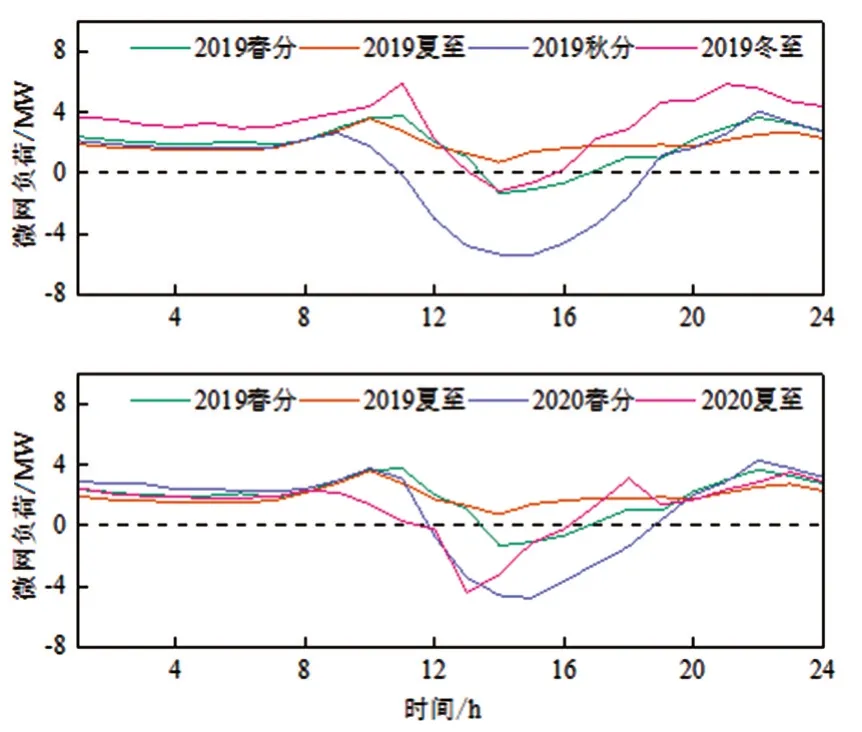
图18 负荷功率与光伏出力差值的变化曲线

计算可得，典型日C部分的最大值为27 MWh，铅晶电池充电效率为95%，储能容量配置26 MWh，放电深度为70%，则可用容量为18.2 MWh。下文将对储能配置过程展开研究，表中z、l表示储能变化前、后的容量。

72 h储能验证如表3、图19所示。

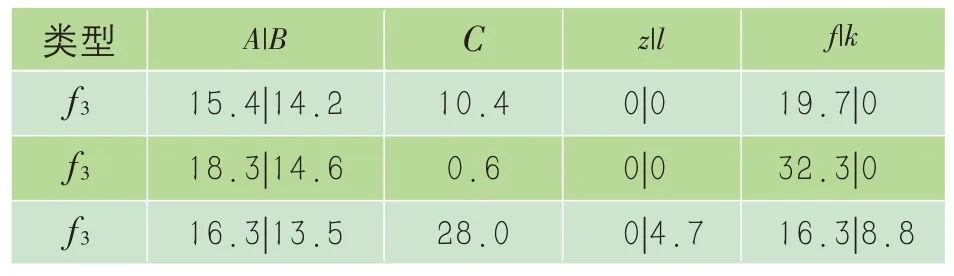
表3 72 h储能配置变化 MWh

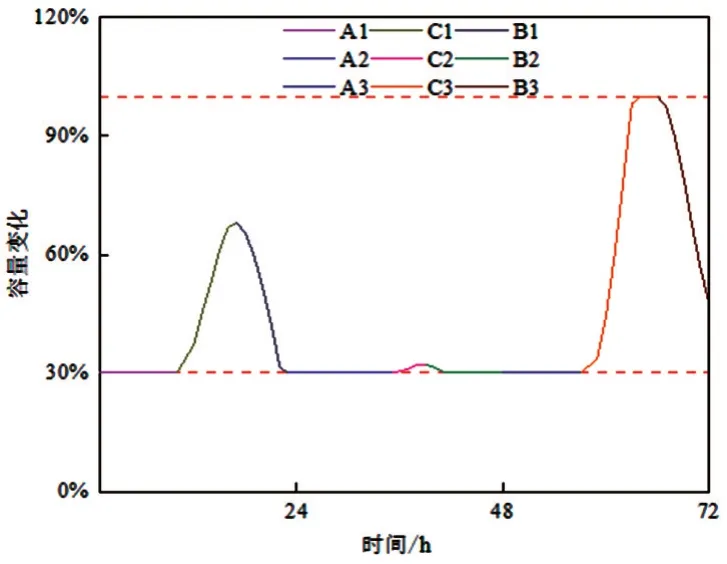
图19 72 h储能容量变化

168 h储能验证如表4、图20所示。

表4 168 h储能配置变化 MWh

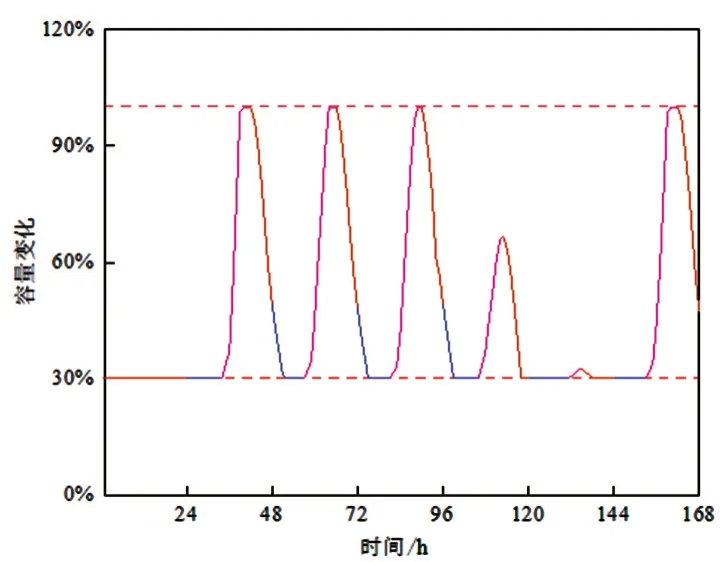
图20 168 h储能容量变化

结果表明，72、168 h 储能利用率分别为17.67%、23.19%，光伏上网电量占总发电量的6.11%、7.83%，未实现光伏本地消纳最大化。

3.1.2 代表日储能配置

以各月代表日数据进行储能配置，代表日C部分最大值为2019.08.16 的32 MWh，配置储能容量为30.4 MWh，可用容量为21.28 MWh。

72 h储能配置及容量变化如表5、图21所示。

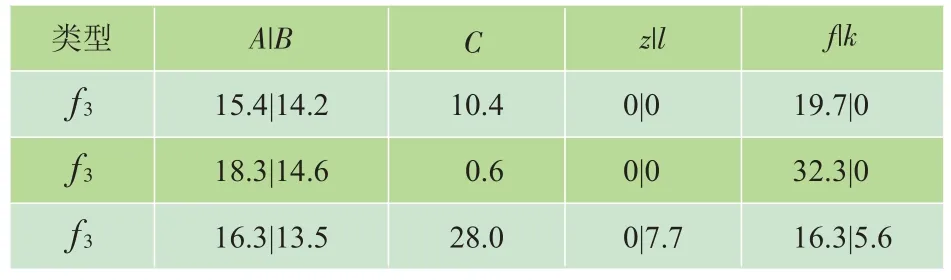
表5 72 h储能配置变化 MWh

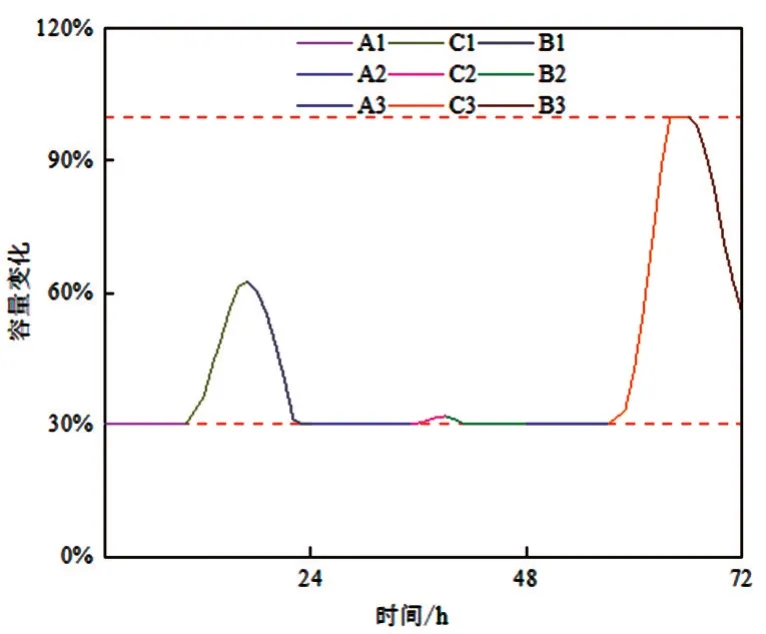
图21 72 h储能容量变化

168 h储能配置及容量变化如表6、图22所示。

图22 168 h储能容量变化

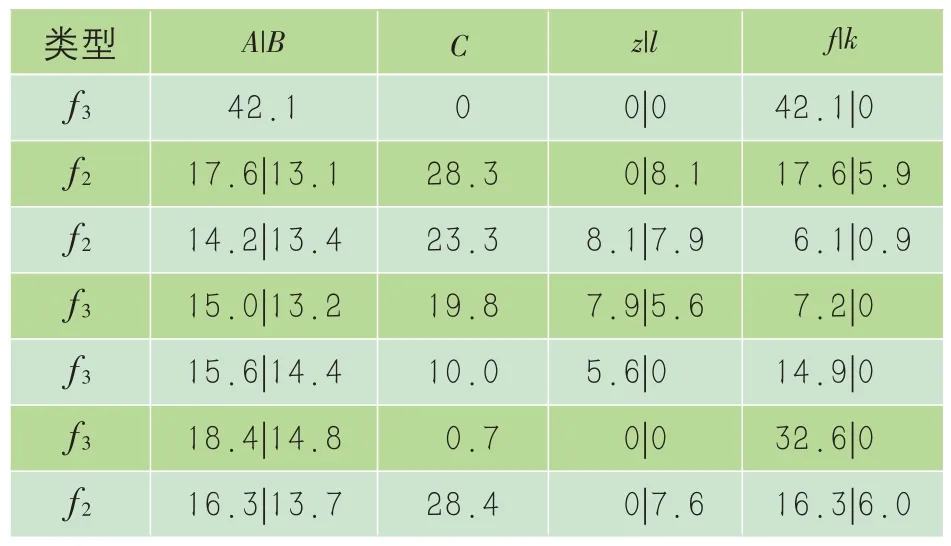
表6 168 h储能配置变化 MWh

结果表明，72 h、168 h 储能利用率分别为16.81%、22.71%，光伏上网电量占总发电量的4.16%、4.27%，相较于典型日，光伏上网量降低，但仍未实现光伏本地消纳最大化。

3.1.3 历史数据储能配置

历史数据中C值变化如图23所示。

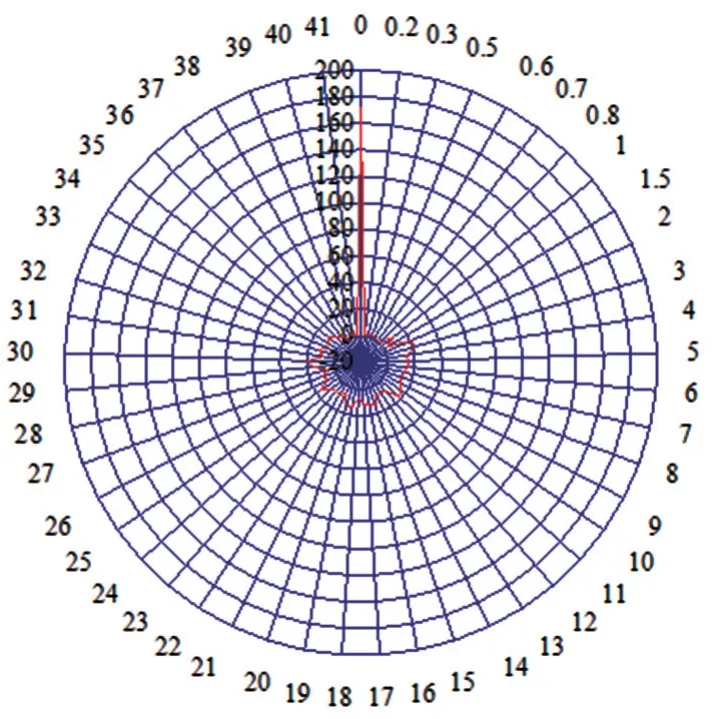
图23 历史数据C值统计

历史数据中C部分最大值为41 MWh，则配置储能容量为39 MWh，可用容量为27.3 MWh。

72 h储能配置及容量变化如表7、图24所示。

表7 72 h储能配置变化 MWh

图24 72 h储能容量变化

168 h储能配置及容量变化如表8、图25所示。

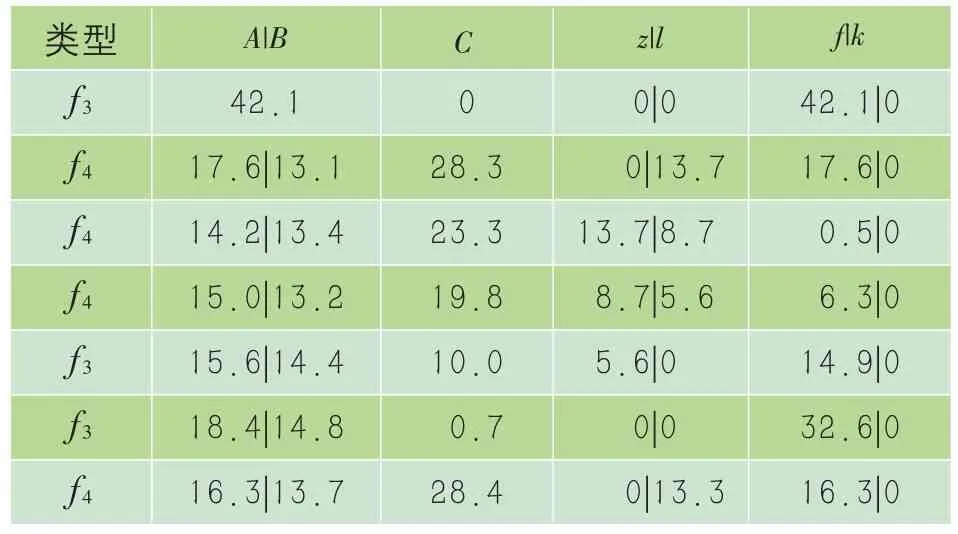
表8 168 h储能配置变化 MWh

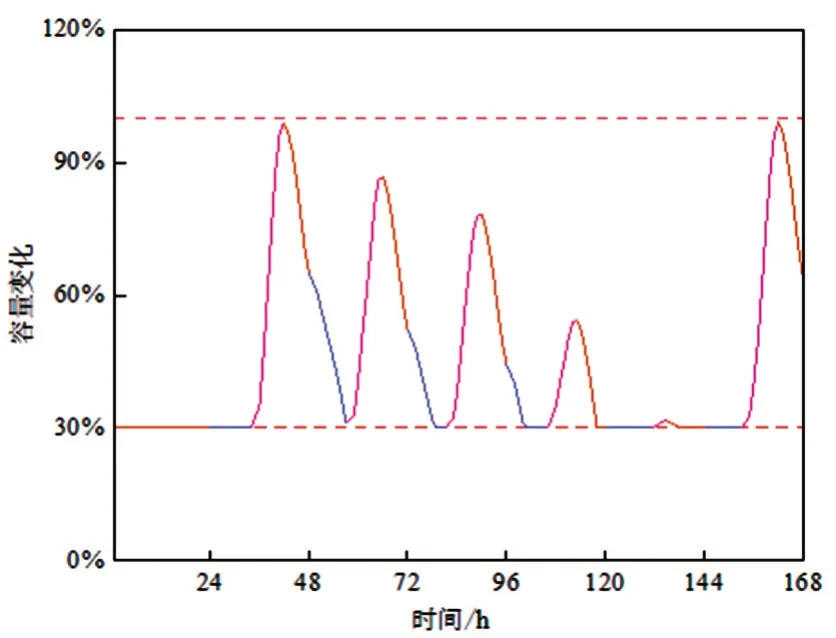
图25 168 h储能容量变化

结果表明，72 h、168 h 储能利用率分别为15.12%、21.04%，光伏上网电量均为0，即实现了光伏消纳最大化，此时须配置24375 节2 V、800Ah的铅晶电池。

3.1.4 实际工程中的储能配置

目前，实际工程中储能配置占比为10%～20%，该文基于历史数据配置一种适用于工程的储能容量。选择出现次数较多的C值，即储能容量为3 MWh。

72 h 储能配置及容量变化如表9、图26 所示。

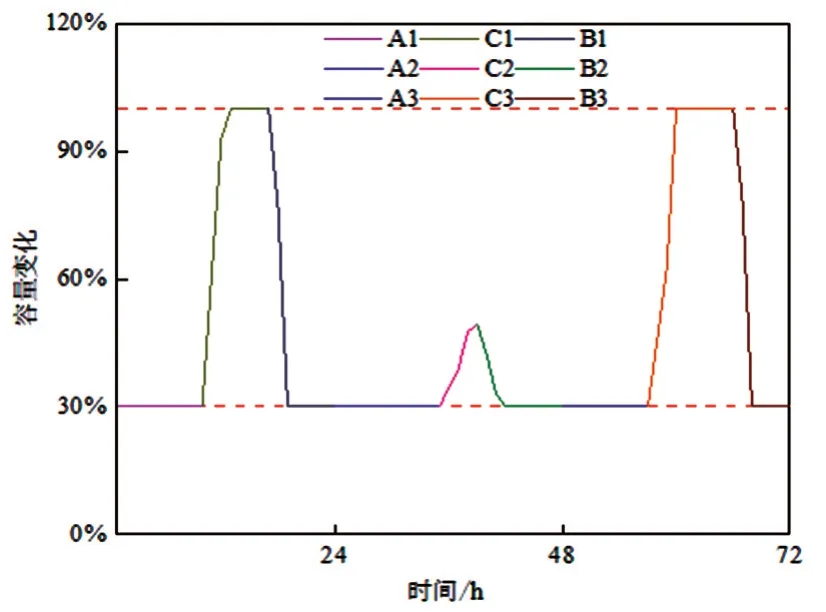
图26 72 h储能容量变化

表9 72 h储能配置变化 MWh

168 h储能配置及容量变化如表10、图27所示。

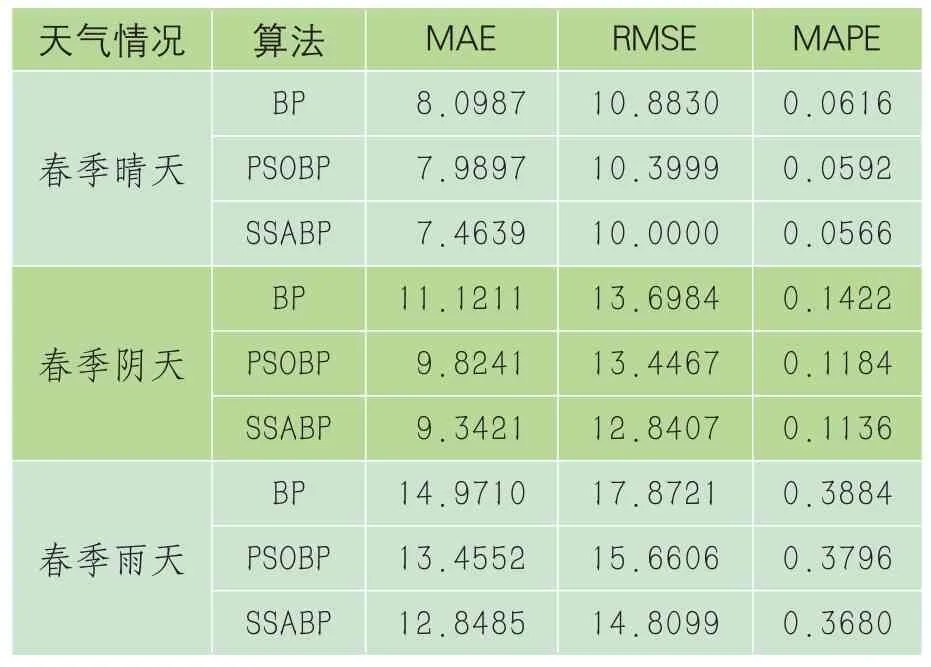
表1 春季预测评价指标 MWh

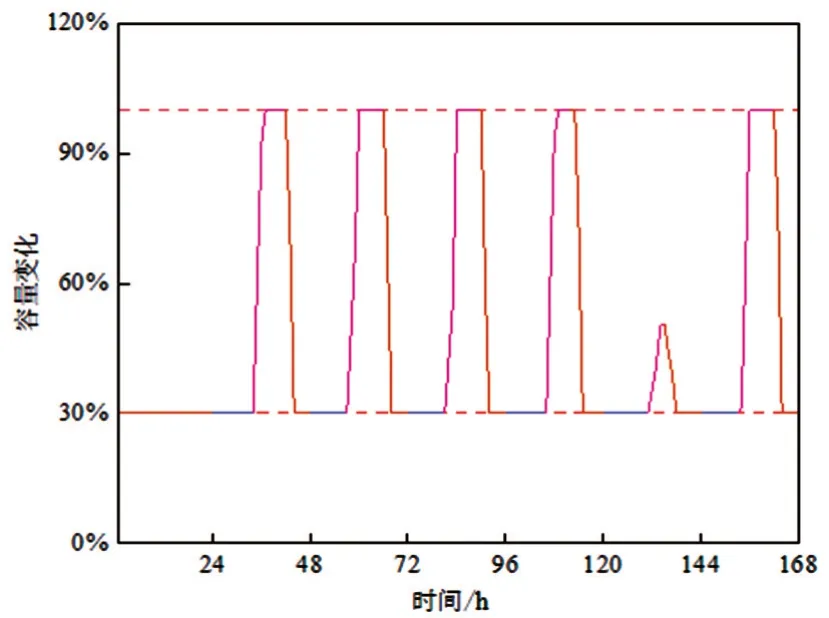
图27 168 h储能容量变化

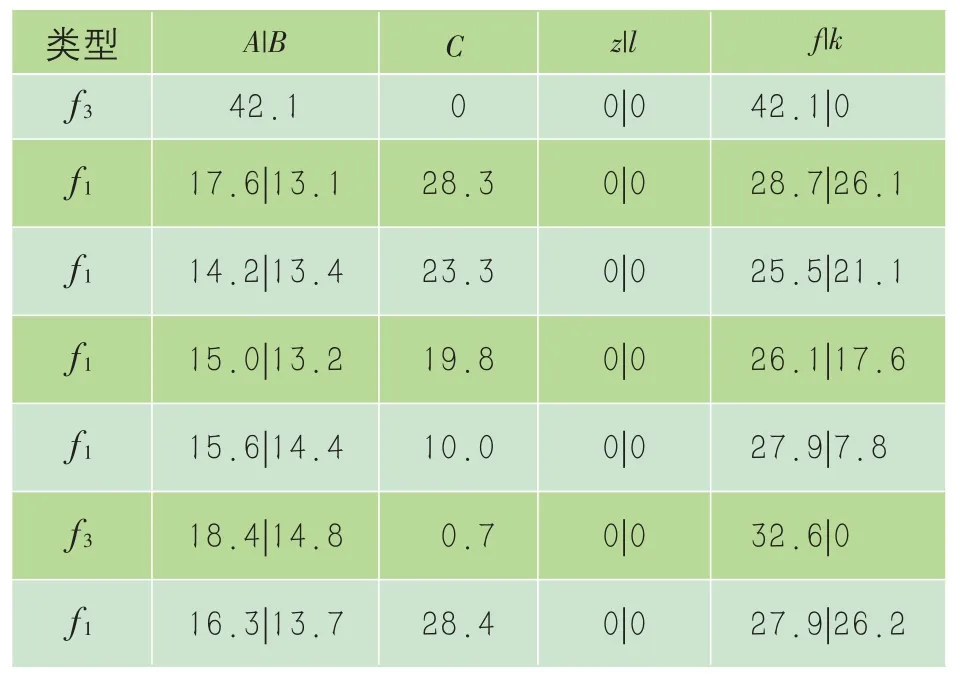
表10 168 h储能配置变化 MWh

结果表明，72 h、168 h 储能利用率分别为22.67%、24.08%，光伏上网电量占总发电量的28.97%、35.74%，光伏上网量较高，未实现光伏本地消纳最大化。

3.2 配置结果分析

通过配置不同容量储能，光伏消纳及上网电量的变化情况如图28、图29所示。

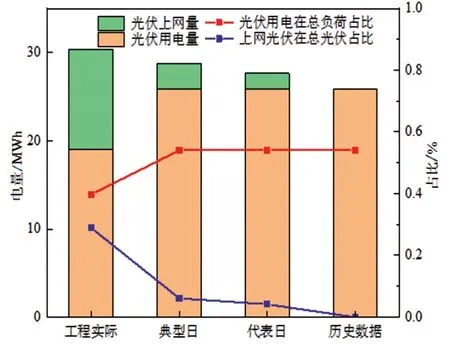
图28 72 h配置对比

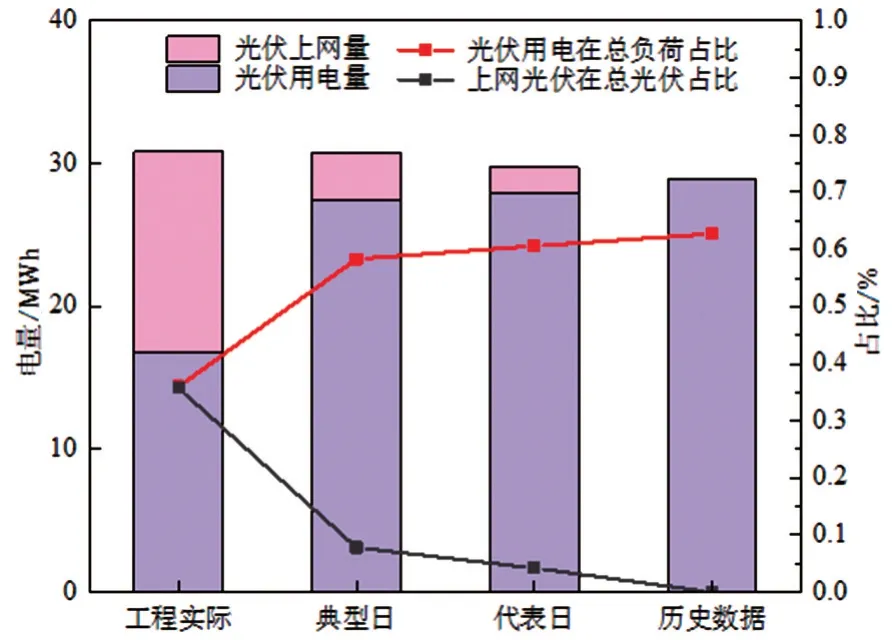
图29 168 h配置对比

结果表明，随着储能容量的增大，光伏消纳不断增加，当储能容量为39 MWh 时，光伏上网量为0，实现了光伏本地消纳最大化。另外，当地受外界环境影响时，不同时间尺度下的储能配置可保证负荷安全稳定高效运行。

4 结束语

该文以陕西省咸阳市彩虹光伏电站及咸阳彬县城关镇330 kV变电站为实验平台，基于电站历史数据，对光伏发电量、用户负荷进行预测，并根据光伏发电量与负荷需求量的差值，进行储能配置分析。得到以下结论。

不同季节及天气类型，光伏发电量的差异性较大，麻雀优化模型在晴天的预测结果更准确，阴雨天稍差，但总体而言，该方法能够提高预测精度及稳定性。

负荷变化具有波动性，选择LSTM 完成了不同时间尺度下的负荷预测，预测精度较高。

4 种储能配置方案中，基于历史数据配置的储能容量，光伏本地消纳接近100%。结合实际工程配置的储能，符合当前能源主管部门对新型电力系统的储能配置要求。