串行布置的多装配尺寸链组公差分配优化设计

张康锋，李蓓智，王庆霞

（东华大学 机械工程学院，上海 201620）

0 引言

在制造业中,公差分配是指在满足零件装配要求的前提下,按照一定的约束条件和优化准则,优化分配各组成环的尺寸公差,同时要尽量符合经济性原则。目前,传统的公差分配方法是通过结合零部件的设计手册和设计经验来确定的。对于一些高精密制造产业,现有的方法不能够完全满足公差分配要求,难以做到出厂产品一致性。另外,若分配给各个零件的公差范围过大,则达不到装配要求,若分配给各个零件的公差范围过小,则会导致加工难度过大,成本急剧增加,因此进一步研究公差分配方法具有重要理论价值和意义。

近年来,国内外许多学者对公差分配方法展开了研究,并取得了一些成果。Tao等[1]提出了新的成本容差模型,该模型考虑了多种替代制造工艺对零件制造成本和质量损失的影响,结合蒙特卡罗仿真和自适应差分进化（SADE）的混合优化算法,在保证高装配精度的前提下实现成本最小化；MarouaGhali等[2]提出了一种基于失效模式、影响和危害性分析（FMECA）和拉格朗日乘数（LM）方法的创新公差分配方法；Xinhui等[3]通过研究车门装配偏差与制造成本的关系,提出集成制造成本和田口工序能力指数的公差分配模型,以粒子群优化算法求解装配体关键特性的最优公差；刘鹏等[4]针对当前机床几何精度建模忽视装配过程中的调整量,以及机床公差分配时缺乏科学可行的方法问题,考虑装配过程中的调整控制量,建立了更加准确的机床装配精度模型,以自适应遗传算法进行求解；吴文等[5]以制造成本和质量损失成本之和最小为目标函数,以概率边界为约束,利用拉格朗日乘数法对公差分配进行求解；王瑜等[6]以加工成本和产品质量稳健性损失成本为目标函数,以模糊度可靠度和可取公差极限范围为约束,利用遗传算法实现了公差的多目标优化设计；郑丞[7]等基于合作博弈理论和装配产品公差稳健设计建模,提出基于Nash仲裁均衡的公差稳健设计方法。

以上研究对象主要针对单一装配尺寸链,只需满足最终封闭环的公差要求即可。但在实际某些零件的装配过程中,需同时满足多个装配要求。因此本文将公差分配拓展到多装配尺寸链。通过构建串行布置的多装配尺寸链组,将每个装配要求分配给其中一条装配尺寸链,然后构建基于加工成本和质量损失的公差分配多目标优化数学模型,采用基于Pareto机制的快速非支配排序遗传算法（NSGA-Ⅱ）,利用MATLAB软件进行模型的求解,进而得到多装配尺寸链组的公差优化分配方案。

1 串行布置的多装配尺寸链组构建

装配尺寸链是指在机器的装配关系中,由有关零件的尺寸或相互位置关系连接而成的封闭尺寸组。如图1所示为航空航天产品复材箱体Z-J2型纵筋与环筋装配示意图,纵筋两个槽口需同时与环筋进行装配。与传统的轴孔配合只需满足一个间隙值目标不同,纵、环筋装配后,环筋与纵筋槽口两侧均需满足一定间隙。如图2所示,采用传统尺寸链构建方法,以纵筋第二槽口与对应环筋右侧面的间隙为封闭环,其余为组成环构建装配尺寸链。由于需同时满足多个间隙值,采用传统的公差分配方法难以计算。因此考虑将单个槽口与环筋重新构成装配尺寸链进行公差分配的计算。如图3所示,以纵、环筋每个右端间隙为封闭环,以纵筋槽口宽度,左端间隙,环筋宽度为组成环构建装配尺寸链,将两组尺寸链组合成为串行布置的多装配尺寸链组,纵筋槽口与环筋的装配尺寸链称为成员尺寸链。进而基于加工成本—公差模型和质量损失模型对多装配尺寸链组进行公差优化分配。

图1 纵、环筋装配示意图

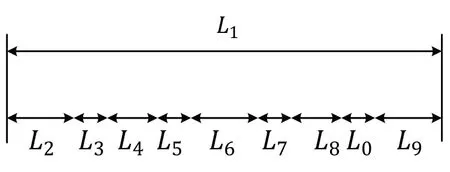
图2 传统尺寸链构建

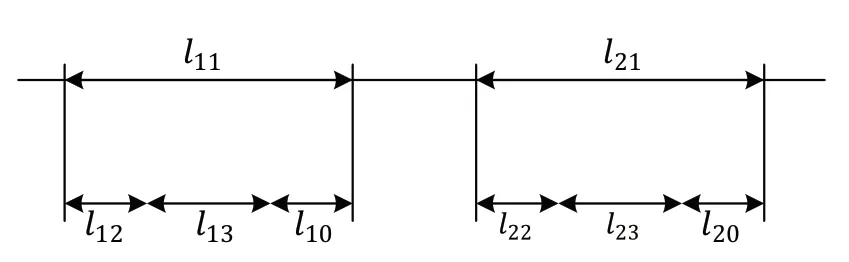
图3 串行布置的多装配尺寸链组

2 数学模型

2.1 加工成本-公差模型

目前国内外许多学者对零件加工成本与公差的关系展开了深入研究。加工成本-公差模型主要可分为以下几种：指数模型、负平方模型、幂指数模型、倒数模型、多项式模型和复合模型等[8]。本文选用负平方模型建立加工成本-公差模型。设串行布置的多装配尺寸链组含n个成员尺寸链,设第i个成员尺寸链由N个组成环组成,则多装配尺寸链组中第i(1≤i≤n)个成员尺寸链的第j(1≤j≤N)个组成环的加工成本可以表示为：

式(1)中：tij为第i个成员尺寸链第j个组成环的公差值；a1,a2为待定系数。它们与加工过程中的具体因素有关,如零件材料,加工方法,零件批量大小,零件结构等。

2.2 质量损失函数

著名日本学者田口玄一第一次提出了质量损失概念,他将质量损失作为连续变量,零件的质量损失随着零件公差值偏离目标值增大而增大。质量损失函数L(x)可表示为：

式(2)中,x为质量特性值,y为零件公差目标值,k为质量损失系数。

当尺寸公差呈对称双向分布时,x-y=t/2,因此可以得出：

则在多装配尺寸链组中,第i个成员尺寸链的第j个组成环的质量损失函数可以表示为：

式(4)中,kij为第i个成员尺寸链第j个组成环的质量损失常数,i=1,2,...,n，j=1,2,...,N。

2.3 多装配尺寸链组约束条件

1）成员尺寸链公差约束

装配尺寸链是由零件尺寸（组成环）和装配要求（封闭环）构成的。在装配过程中,尺寸链的封闭环公差对零件的加工尺寸具有重大影响。装配公差约束可以选用两种方法：极值法和统计法。本文以极值法公差分配为依据,成员尺寸链中的组成环与封闭环具有如下约束关系：

式(5)中,tij第i个成员尺寸链第j个组成环的公差值,ti0第i个成员尺寸链封闭环公差。因此,多装配尺寸链组成员尺寸链公差约束为：

式(6)中,i取1～n。

2）原装配尺寸链公差约束

串行布置的多装配尺寸链组是由原装配尺寸链转换而来,需满足原装配尺寸链装配要求,以极值法引入装配约束条件,其中不参与多装配尺寸链组的组成环以原始公差进行赋值,其表达式为：

式(7)中，Ti为原装配尺寸链的第i个组成环，T0为原装配尺寸链的封闭环。

3)加工能力约束

在实际加工过程中，受限于机器人，机床等设备的加工精度、运动性能和功能指标等因素，需将公差的取值极限考虑进去，即装配尺寸链中各组成环的公差不能超过加工设备的加工能力,其表达式为：

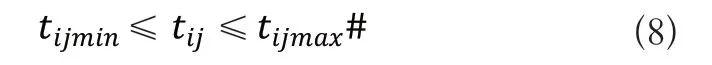
式(8)中,tijmin和tijmax分别为第条成员尺寸链第个组成环加工能力公差上极限和下极限。

2.4 模型建立

综上所述,以总加工成本和总质量损失两个函数作为优化目标,以成员尺寸链公差、原装配尺寸链公差,加工能力作为约束条件,建立串行布置的多装配尺寸链组公差优化分配模型。模型的表达式为：

3 基于Pareto最优概念的多目标优化问题求解

针对多目标优化问题求解,一些传统的优化算法如粒子群算法、遗传算法、蚂蚁算法等通常将多目标问题转化为单目标问题后进行求解,计算时常常陷入局部最优,导致这些传统的优化算法很难找到使多个目标函数同时取得最优的解。意大利经济学家维弗雷多·帕累托在1896年首次提出了非支配解概念,后被称为Pareto最优解概念,目前,有大量学者对基于Pareto最优解概念求解多目标优化问题进行了研究。

与传统的优化算法不同,Pareto遗传算法得出的Pareto最优解并非唯一的,而是由多个解形成的最优解解集,最优解集在空间中形成的曲面称之为Pareto前沿[9]。一般多目标优化问题可以表示为如下形式：

式(9)中,x为d维决策向量,f(x)为目标向量,N为优化目标数量；gi(x)和hj(x)分别为第i个不等式约束和第j个等式约束。

基于Pareto架构,Deb K等[10]对非支配排序遗传算法（NSGA）进行了改进,提出了带精英策略的非支配遗传算法（NSGA-Ⅱ）。该算法引入了精英策略,保证在进化过程中某些优秀种群个体不会被遗弃,提高了优化精度。NSGA-Ⅱ的基本思想为：

1）随机产生规模为N的初始种群,非支配排序后通过遗传算法的选择、交叉、变异三个基本操作得到第一代子代种群；

2）从第二代开始,将父代种群与子代种群合并,进行快速非支配排序,同时对每个非支配层中的个体进行拥挤度计算,从而组成新的父代种群；

3）通过遗传算法的基本操作产生新的子代种群：依此类推,直到满足程序结束的条件。

NSGA-Ⅱ流程图如图4所示。

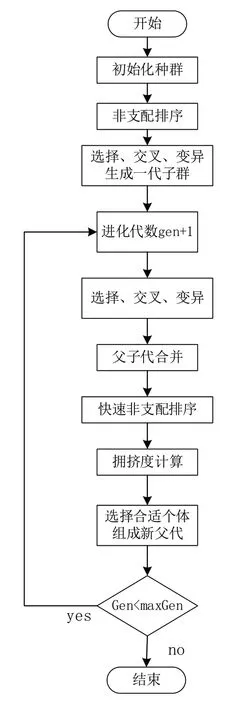
图4 NSGA-Ⅱ流程图

4 实例分析

本文以某航天企业产品复材箱体中的Z-J3型纵筋（3槽口）与环筋装配为例进行验证。原装配尺寸链和串行布置的装配尺寸链组如图5和图6所示,其中成员尺寸链为三个纵筋槽口与环筋的装配尺寸链。设原装配尺寸链中的组成环尺寸为Li，封闭环为L0；设串行布置的多装配尺寸链组中第个成员尺寸链第个组成环的尺寸为lij，公差值为tij,根据企业设计书要求,各成员尺寸链封闭环公差要求分别为必须小于0.3mm,0.4mm,0.3mm。原装配尺寸链封闭环需小于1mm。

图5 Z-J3型纵、环筋装配尺寸链

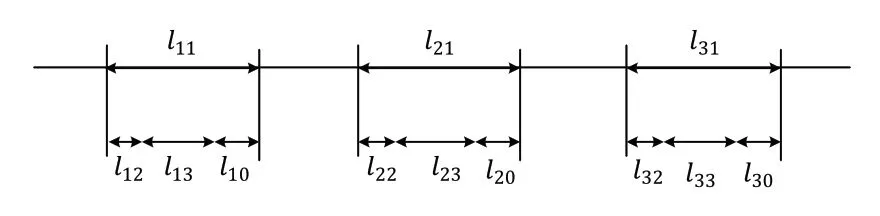
图6 串行布置的多装配尺寸链组

本文通过式(1)的负平方模型来描述纵、环筋装配过程中各公差与加工成本的关系,在企业协助下,对生产厂中实际生产数据进行拟合,得到纵、环筋多装配尺寸链组的模型参数值a1,a2如表1所示。

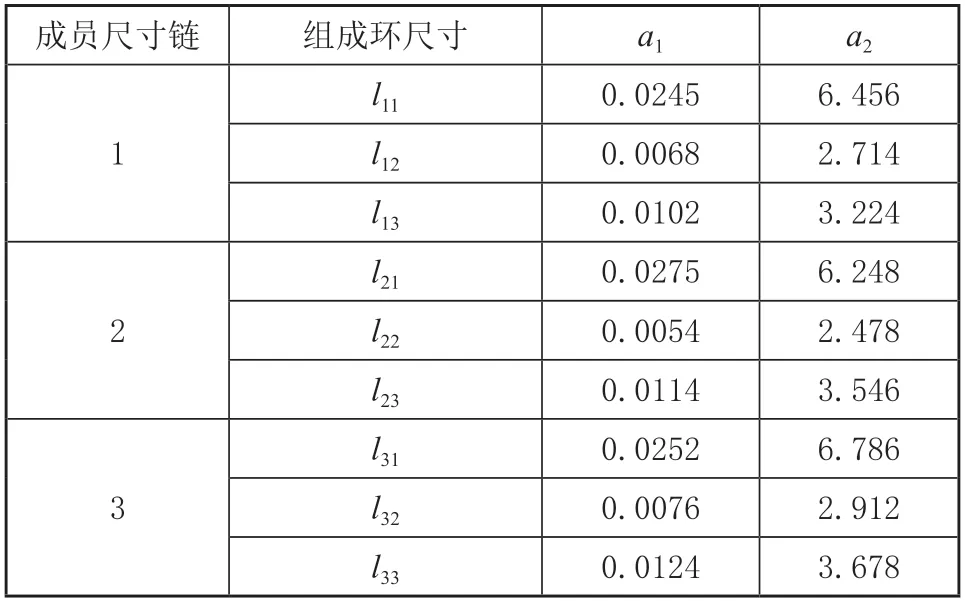
表1 各组成环参数

同时在企业帮助下,统计了多装配尺寸链组的质量损失成本。其中,成员尺寸链中的对应位置组成环具有相同质量损失常数,所有公差皆为双向对称分布,质量损失成本函数如式(13)～式(15)所示：

基于以上分析,可得纵、环筋装配尺寸链组的加工成本—质量损失的公差优化模型如下：

目标函数：

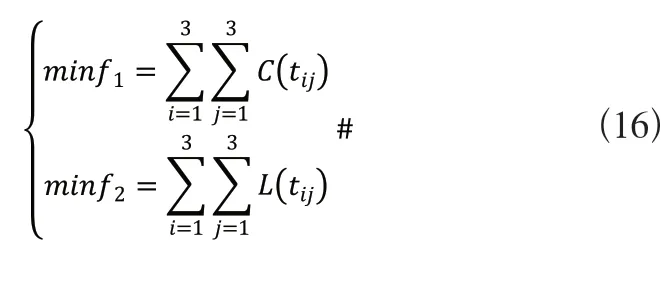
约束条件：

1）成员尺寸链装配公差约束

2）原装配尺寸链装配公差约束

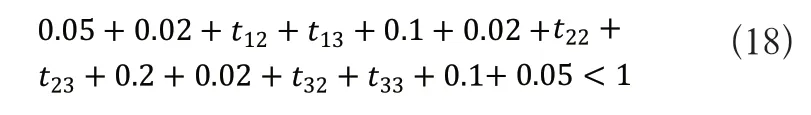
3）加工能力约束

使用MATLAB软件迭代300次后求解结果如图7所示。从Pareto前沿图中可以发现曲线在总制造成本f1＜120时,总质量损失的变化幅度远远大于总制造成本的变化,在此阶段减少总制造成本将会造成总质量损失急剧增加,导致质量损失过大；当曲线在120＜f1＜160时,改变总制造成本对总质量损失具有显著影响：增加总制造成本,总质量损失明显降低；减少总制造成本,总质量损失明显增大；当曲线在f1＜160时,增加总制造成本并不能使总质量损失明显减少,若执意追求零件质量,会导致总制造成本大大增加,而质量损失减少非常缓慢。

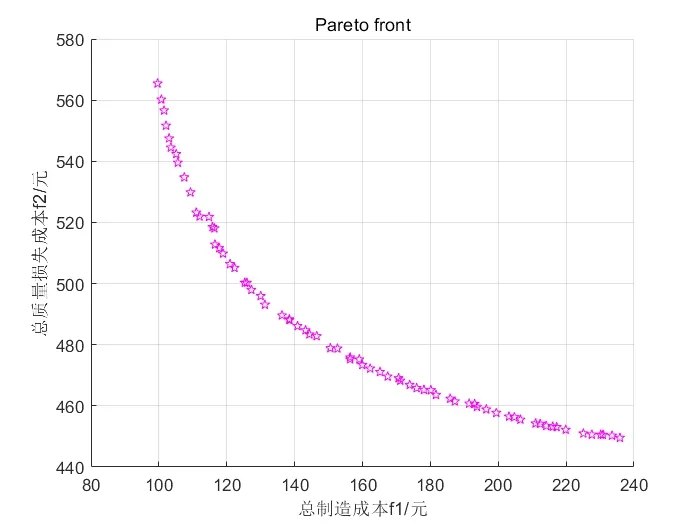
图7 Pareto最优前沿

5 结语

本文以航天产品复材箱体中的纵筋与环筋装配为研究对象,构建了纵、环筋串行布置的多装配尺寸链组,基于加工成本—公差模型和质量损失模型,以成员尺寸链公差,原装配尺寸链公差和加工能力为约束条件,建立了串行布置的多装配尺寸链组多目标公差优化分配数学模型。采用带精英策略的非支配排序遗传算法（NSGA-Ⅱ）在MATLAB软件中进行求解,从而得到分布均匀的总制造成本—总质量损失Pareto前沿曲线图,曲线图中的点集可为公差分配方案提供多种解决方案和理论依据,从而统筹兼顾产品的质量和成本。