基于贝叶斯网络的 全自动运行系统弹性评估
吴乃哲
(北京市轨道交通运营管理有限公司,北京 100068)
1 研究背景
全自动运行系统(fully automatic operation,FAO),是基于现代计算机、通信、控制和系统集成等技术来实现列车运行全过程自动化的新一代城市轨道交通系统。全自动运行系统是一项系统工程,涉及信号、车辆、综合监控、通信、站台门、车辆基地等多个专业,以行车为核心,通过信号、车辆、综合监控、通信系统的深度集成,提升轨道交通运行系统的整体自动化水平。FAO 信号系统是关键设备,可以控制列车运行,保证行车安全,提高运输效率,传递行车信息,改善行车人员的劳动强度。FAO 信号系统是当前城轨主流信号系统CBTC(基于通信的列车运行控制系统)的升级版,在CBTC 的基础上,增加了包括列车休眠唤醒、动静态自检、障碍物/脱轨防护、远程复位等20 余项功能,具备高度自动化和深度集成、充分的冗余配置、完善的安全防护、丰富的控制中心功能,且完全兼容常规的CBTC。随着全自动运行系统技术的逐渐发展,越来越多的国家和城市选择采用了自动化程度更高、运行性能更稳定的全自动运行系统。在我国,随着燕房线等全自动运行线路的开通,在国家大力倡导发展智慧城轨的趋势下,未来FAO 信号系统必将代替CBTC 成为城轨信号系统的新主流。
城市轨道交通与地面公交相比,具有载客量大、运行轨道单一的特点。这意味着列车一旦出现运行故障,不仅影响自身的列车运行以及所载乘客的正常出行,而且也会影响后续列车的运行,因此轨道交通系统的运行故障影响有传播面广、发展迅速的特点。即使全自动运行系统已经在CBTC 的基础上提升了安全水平,降低了系统发生故障的可能性,但故障的发生仍是不可能被完全杜绝的。为了进一步提升全自动运行系统的安全水平,研究人员也需要考虑当故障发生后,如何将故障影响降到最低,即系统能够抵抗故障,减缓故障产生的性能下降速度,并且快速恢复弹性能力。
弹性(resilience)一词源于拉丁文resiliere,为回弹的意思。该词最早由生态学家Holling[1]引入生态学领域,用于衡量系统可持续性、吸收变化和扰动后维持种群关系的能力,之后这一概念逐渐扩展到组织管理、基础设施、工程系统等领域,广泛用于评价个体、集体或系统承受扰动以及扰动后的恢复能力。自然灾害、设备故障和人为失误等都可能对组织或系统的连续运行造成潜在和严重的威胁,这些极端自然事件和技术事故之后伴随的灾害和危机的发生,都显示出传统风险评估和管理的局限性。在风险的背景下,弹性已被作为常规风险管理的补充和替代方案进行讨论。为了应对众多的大规模意外事件,如轨道交通系统中严重的意外事故,弹性分析成为大型复杂基础设施系统的最佳决策,同时也可作为对于复杂系统自适应管理具有重要意义的风险管理分析的补充。
弹性评估方法从大体上可分为定性、半定量以及定量3 种类型。定性评估的思路主要是分析影响系统弹性的因素,并根据弹性影响因素建立弹性评价框架,对系统展开弹性评估。例如,两组研究人员都根据自身系统的特点,各有侧重地建立了用于定性分析的弹性评估框架[2-3]。半定量评估方法通常是利用定性评价来获取源数据,继而使用数学模型进行定量计算。例如,Muller 采用模糊规则评价法评估了基础设施系统的整体弹性[4];Azadeh 等采用数据包络分析法对石油化工厂系统进行弹性计算,同时还用模糊认知图对系统弹性进行评价[5]。定量评估方式则是通过获取真实事件的数据或者通过模拟仿真得到的数据,采用一定的数学模型进行计算。例如,魏群通过对列车运行过程进行模拟仿真获取原始运行数据,将列车运行间隔和延误时间作为性能指标,采用弹性曲线模型的方式评估系统弹性[6]。
城市轨道交通系统的弹性研究还处于较为初级的阶段,而随着全自动运行系统的不断发展,为保证该系统能以更高安全水平的方式运行,除了采取传统的风险管理方式外,提升系统的弹性、使系统更具有“韧性”也是不能忽视的。为此,本研究提供一种基于贝叶斯网络模型的弹性评估方法,从全自动运行系统的弹性特点出发,从宏观到微观的逻辑思维,探究了全自动运行系统内部以及外部的弹性因果关系,通过敏感度分析,对弹性影响因子进行敏感度排序,理清影响系统弹性的主要因素,为提升全自动运行系统弹性提供指导意见。
2 理论基础
2.1 贝叶斯公式
贝叶斯统计推断起源于英国学者Bayes 发表的一篇论文,他在这篇论文中提出了著名的贝叶斯公式。1988 年,Pearls 深入分析了拓扑结构以及变量间的条件独立性关系,提出了贝叶斯网络(Bayesian Network,BN)。贝叶斯公式是贝叶斯网络进行推断和计算的理论基础,如果事件B1,B2,…,Bn是彼此互斥的事件,且这些事件构成一个完整事件,并且有 P(Bi)≥0 (i=1, 2, …, n),同时有事件A,且A 与B1, B2, B3, …, Bn中的事件同时发生,则贝叶斯公式可表示为

式中:P(Bi)表示先验概率,它一般是观测者根据先验知识主观判断得到的概率或是根据现有的统计数据及历史资料计算得到的概率;P(Bi|A)表示后验概率,它是先验概率在经过贝叶斯公式进行修正计算后得到的更符合实际的概率;P(A|Bi)表示条件概率,它是指在事件B 己经发生的条件下事件A 发生的概率。
2.2 贝叶斯网络
贝叶斯网络又称信度网络,是贝叶斯方法的扩展,是目前不确定知识表达和推理领域最有效的理论模型之一。贝叶斯网络用二元组BN=(G,P)来表示,其中G=(N,E)用来对网络结构进行定性的描述,代表一个有N 个节点的有向无环图,E 是有向无环图中边的集合;P 代表条件概率表,贝叶斯网络中的节点与其条件概率表相关联,该表用于确定节点状态在其父节点条件下的概率,没有父节点的用先验概率进行信息表达。节点之间的相互依赖关系由联合概率分布来定义,因此全贝叶斯网络结构的联合概率可以使用链式规则计算所有“父项”的因子分解形式。这样,包含n 个变量的贝叶斯网络的全联合概率分布P(B1, B2, …, Bn)可以表示为
式中,Pa(Bi)为节点Bi的父节点集。
2.3 网络的学习
贝叶斯网络学习包括网络的参数学习与网络的结构学习两种。贝叶斯网络的参数学习是在已知确定的贝叶斯网络拓扑结构的条件下,确定与有向无环图中每个节点相关的条件概率分布。贝叶斯网络的结构学习是在已知网络中节点数量与状态的情况下,利用先验知识及数据经验,结合训练样本集的方法,确定合理的贝叶斯网络拓扑结构。
一般情况下,贝叶斯网络的学习主要基于两个假设条件:一是数据集中每个记录的数据服从统一的概率分布,二是网络参数θ 同时满足局部独立性和全局独立性的假设。
当具有完整数据集时,最常采用的参数学习方法是最大似然估计法和贝叶斯方法,但在现实情况中,收集的数据可能会有不同程度的缺失现象。当对具有缺失数据的贝叶斯网络进行参数学习时,可采用最大期望算法(expectation-maximization algorithm,EM),EM 算法的实质是设法将不完备的数据转化为完备数据。
EM 算法主要由两个步骤完成,即E 步骤计算期望和M 步骤最大化。通过对这两个步骤的反复迭代,直到算法收敛,从而计算出未知参数的估计值。实际上,计算期望值就是计算对数似然函数的下界值:设X 为未知变量,Y 为观测变量,D 为训练集,定义q(X=x|Y)表示当观测值为Y 时X=x 的概率,可以得到
设对数似然函数L 为

假设函数P(X=xi,Y=D)为有极值的凸函数,则根据Jensen 不等式可以得到

EM 算法实际就是在E 步骤得到参数的下界,在M 步骤进行更新计算,得到其最大值。令q(X=x|Y)= P(X|θt),θt代表当前迭代结果的未知参数,θt+1为下一次迭代的参数,求解L 的下界其实就是在给定当前参数的条件下求下一次迭代的参数,L 的下界设为Q(θt+1|θ),则:

按照最大似然估计中的方法,求出Q(θt+1|θ)最大时参数,有

式中,ENijk表示数据集D 中满足Xi=xik,Pa(Xi)=Pa(Xi)j,即满足当节点i 的值取第k 个值时对应的父节点为j的数据。
3 模型构建
3.1 网络架构
弹性研究在工程系统、电力系统、交通网络等领域都得到了有效的应用,到目前为止还没有形成统一的弹性定义,但总结起来大致相似,都关注于系统对扰动的承受和恢复能力。Bruneau 在其论文中,用系统在遭受扰动前后的性能变化曲线来刻画弹性[7],如图1 所示。通过弹性曲线的描述,系统的弹性能力可以在扰动前后的4 个不同阶段来体现:阶段1,体现系统在未遭受严重扰动时能保持正常运行,同时能实现目标运力;阶段2,在系统遭受来自内部或外部的干扰后,系统性能开始下降,这一阶段能够体现系统抵抗性能下降的弹性能力;阶段3,系统逐渐开始恢复,主要体现了系统恢复的快速性;阶段4,描述了系统再次恢复稳定后的性能水平,体现了系统弹性的恢复完备性。

图1 性能“下降-恢复”曲线 Figure 1 “Failure-recovery” performance curve
因此,通过弹性曲线的直观描述,可以得到弹性由4 种弹性能力来体现,如图2 所示。
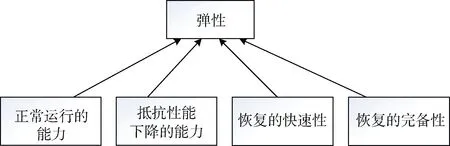
图2 弹性的四大能力 Figure 2 Four abilities of resilience
Murray-Tuite 首次提出了关于弹性在交通运输领域的定义,同时还提出了交通系统弹性的量化方法,他认为弹性包含多个维度,分别是冗余性、多样性、有效性、部件的自主性、协作、适应性、移动性、安全性以及迅速恢复等[8]。从RAMS 角度可以发现,系统的可靠性、可用性及可维修性等静态指标越好,系统能够正常运行的能力就越强;而系统弹性除了受RAMS 静态指标的影响,由扰动引发的系统性能下降以及性能恢复过程也体现了弹性的动态特性。另外,从全自动运行系统的功能实现角度可以发现,系统的正常运行同样离不开人员的参与,而在发生故障时能否有效恢复,与人员的工作效率有很大关系,因此全自动运行系统的弹性也受人员组织的影响。专业研究认为,弹性是一个系统在变化和干扰之前或之后调整其功能的内在能力,能帮助系统在发生重大事故或在持续压力的情况下也能维持运行[9]。为了具有弹性,一个系统或一个组织必须具备以下4 个品质:一是能以稳健而灵活的方式应对常规和非常规的威胁;二是监视正在发生的事情,包括它自己的表现;三是预测风险(风险事件);四是能从经验中学习。
表1 归纳总结了关于全自动运行系统的弹性评估贝叶斯网络模型的各节点元素,从弹性的四大能力出发,探究其影响因素,并确定表征影响因素的指标作为根节点。

表1 全自动运行系统的贝叶斯网络节点 Table 1 Bayesian network nodes for a fully automatic operation system
3.2 条件概率
在确定了全自动运行系统的弹性贝叶斯网络模型的节点变量后,需要为各节点设置条件概率,明确子节点对父节点的依赖关系。在本研究中,基础节点(无父节点)的先验概率由统计专家的打分结果来获取,为每个基础节点设置2、1、0 三个分值,采集10 位专家的打分结果,其中贝叶斯网络模型的各节点分别设置high、medium 和low 三个状态,再统计每个分值的占比。例如,若有两位专家为该基础节点打2 分,则该节点的high 状态对应的先验概率为40%。
在确定了基础节点的先验概率后,需要为其余有父节点的子节点确定条件概率。确定方式为:将每个节点的high、medium、low 三个状态分别对应2、1和0 分,为了获得子节点的条件概率,计算父节点的数值之和,然后除以它们的最大值之和,为子节点构建一个介于0~1 之间的全局相对值x,有
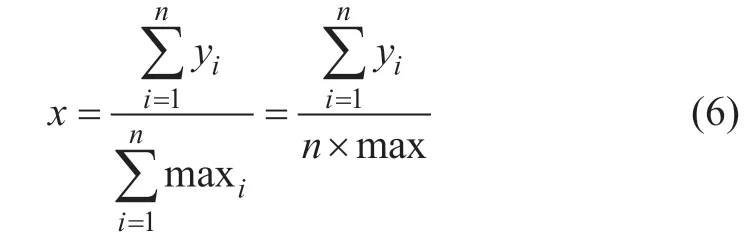
式中,x 是被分析子节点的全局相对值,i 代表该子节点的父节点。
在获得子节点的全局相对值后,用公式x2、2x(1-x)、(1-x)2分别进行计算,再分别对应该子节点在父节点时的high、medium 和low 三种状态的条件概率值。这种分配方式确保了分配的规范化和连续的参数化,若子节点只有成功和失败两种状态,则全局相对值x 则可代表成功的概率。在模糊理论中,这些方程称为隶属函数(membership function,MF)。隶属函数是一条曲线,它定义了如何将输入空间中的每个点映射到0~1 之间的成员值(或隶属度)。其中,将x值转换为隶属度称为模糊化。有较多的隶属度公式可供选择,如三角隶属度公式:当x 介于(0,0.5)之间时,隶属度公式为(-2x+1,2x,0);当x 介于(0.5,1)之间时,隶属度公式为(0,-2x+2,2x-1)。无论使用哪种成员函数,任何点的总和都应始终等于1。在本研究中,选择了一组连续的隶属函数。为了更清楚地展示该过程,以表2 为例,计算一个假设有4 个父节点的子节点的条件概率。

表2 给定父节点状态的子节点的条件概率 Table 2 CPT of a Son node, given the states of the father nodes
4 弹性分析
本研究采用GeNIe 的贝叶斯网络建模软件,GeNIe使用EM 算法对贝叶斯网络的参数进行学习,使用联合树的方法对贝叶斯网络进行推理,且可视化窗口操作方便、学习速度快、计算精度较高,因此比较适合全自动运行系统的贝叶斯网络的构建与分析。在表1中,确定了全自动运行系统的贝叶斯网络模型的节点,同时简单梳理了各节点之间的因果关系。在本研究中,贝叶斯网络大致可以划分为3 个部分,第一部分为四大弹性能力,第二部分是影响因素层,第三部分为指标层[10]。本研究以北京地铁燕房线为例,对指标层制定打分表,采集了10 位专家的打分意见,按照上文中先验概率和条件概率的确定方式,绘制出了全自动运行系统的贝叶斯网络模型,如图3 所示。其中,黄色表示指标节点,绿色表示弹性能力节点,紫色表示弹性节点,其余的节点为影响因素节点。可以看到最终全自动运行系统的弹性结果:高的占比为23%,中等的占比为41%,低的占比为36%,因此最大可能为中等水平。向最终的弹性节点输入状态为高的证据,可以看到各指标的数据变化,可以指导专业人员更好地提升系统弹性。

图3 全自动运行系统的贝叶斯网络模型 Figure 3 Bayesian network model of a fully automatic operation system
通过灵敏度分析,帮助了解贝叶斯网络概率参数对目标节点的影响程度;根据网络参数的微小变化,探究目标节点的变化程度。识别灵敏度高的节点,可以直接指导系统的弹性提升工作。在GeNIe 软件中,可以直接进行灵敏度的分析,在给定一组目标节点的情况下,有效计算每个贝叶斯网络数值对目标节点的后验概率分布的导数。这些导数表明了网络数值参数对计算目标后验概率的重要性,参数p 的导数大,会导致目标在给定参数p 变化的情况下后验变化很大,说明目标节点对该参数变化的灵敏度较高;如果导数很小,那么即使参数的变化较大,也不会对后验产生很大的影响,因此说明目标节点对该参数的灵敏度较差。
在执行灵敏度分析时,目标节点的每个状态都被单独处理。因此,灵敏度分析显示了目标节点在所选状态的最敏感参数。如图4 所示,分别是系统弹性节点以及4 个弹性能力节点在状态高的条件下的灵敏度分析。当参数在选定范围内更改时,所选择的是参数左右波动10%,条形图显示目标状态中的更改范围,笔者选择绘制了10 个最有影响的参数。条形图的颜色表示目标状态变化的方向,红色表示负变化,绿色表示正变化。从中可以清楚地看到,目标节点对每个参数变化的敏感度都不同,状态为高的弹性目标节点对状态为低的参数P8 最为敏感;当参数P8 状态为低的概率下降10%后,系统弹性为高的状态概率从23.29%提升到了24.47%。因此,若想更好地提升系统弹性,首先可以从改善参数P8(也就是系统故障后的维修时间)入手。在对弹性四大能力的敏感度进行分析后发现,最为敏感的参数主要集中在P8、P7 以及P1。可以发现,全自动运行系统在故障后有导致严重事故后果的特征,这决定了该系统的故障恢复过程较为缓慢,因此极大地影响了系统的弹性。另外,人员的工作能力也对系统弹性产生较为严重的影响。

图4 弹性节点在状态为高的敏感度分析 Figure 4 Sensitivity analysis for resilience with a high state
5 结语
笔者基于贝叶斯网络建模方法,提出一种对列车全自动运行系统的弹性评估方式,通过划分弹性能力、影响因素以及指标,确定全自动运行系统的贝叶斯网络节点,通过理清节点之间的因果关系,确定各节点之间的网络结构,建立全自动运行系统的贝叶斯网络模型。通过对指标层制定打分表,确定基础节点的先验概率,同时采用一定的隶属度分配方法来确定条件概率;在输入模型中进行系统弹性计算,结果发现在状态为高、中、低的概率占比中,系统弹性状态为中的占比最大。因此可以说明,以北京地铁燕房线为例的全自动运行系统的弹性水平为中等的概率最大。对目标节点进行敏感度分析可以发现,系统弹性目标节点对参数P8(即故障维修时间)在状态为低时的敏感度最大;同时,通过弹性四大能力的敏感度分析发现,最为敏感的参数集中在P8、P7 以及P1。因此,提升全自动运行系统的弹性,应该重点关注故障维修时间、故障严重程度以及人员工作能力这三个方面。

