资源型经济转型背景下工业能-水消耗时空关联研究
——以山西省为例
王文智,李 琦
(1.山西大学 经济与管理学院,山西 太原 030006;2.东北师范大学 数学与统计学院,吉林 长春 130024)
一、引言
过去几十年来,我国经济发展迅速,为国家实现工业化和现代化奠定了坚实的基础,进入新世纪可持续发展理念开始在全球盛行,我国也积极行动。2010年国务院批复山西省建立国家资源型经济转型综合配套改革试验区,拉开了山西经济转型的序幕,作为全国重要的原材料和能源供应基地,山西省综合改革试验区的设立具有重要的先行和示范意义。十九大报告提出经济发展质量变革的成功要通过提高全要素生产率和建立健全绿色低碳可持续发展的经济体系来实现,山西省通过深化改革,优化升级产业结构和调整经济结构,加快科技进步和创新的脚步,实现低碳、绿色、循环、可持续发展,统筹城乡发展,建立保障和改善民生的综合改革试验区。
以工业为主的经济结构为山西省经济社会发展做出了重大贡献,而作为工业领域大量消耗的能源,清洁和高效利用已迫在眉睫,改革试验区的设立使得提高工业领域的资源等生产要素利用效率,推进工业领域的能源消费改革成为实现绿色低碳循环发展的必由之路。水资源是工业领域重要的生产要素,山西省水资源短缺,所以要提高水资源的生产要素利用率。水资源的高效利用离不开能源的投入,而能源的开发利用也离不开水资源的投入,能源和水资源紧密相关。以煤炭为主的工业产业作为山西省的支柱型产业,往往既是“耗能大户”也是“耗水大户”,是碳排放和水体污染的关键主体。因此,分析山西省工业领域中水资源和能源的配置关系,以及它们和经济增长的关系,对山西省资源型经济转型有重要意义。
本文基于山西省2005—2018年的统计数据,建构工业能源耗水系数,并运用空间自相关方法分析山西省工业领域能-水消耗的时空演变规律;在此基础上采用面板向量自回归模型分析水资源、能源、经济三者的关系,以此来寻求可持续经济发展对能源和水资源使用的要求。
二、文献综述
进入新世纪全球气候和环境变化对人类的经济社会发展提出了严峻挑战。在此背景下,以低能耗、低污染、低排放和高效能、高效率、高效益为特征的低碳经济受到广泛关注,低碳化已经成为世界经济未来发展的必然趋势。但这对于经济处于快速增长的发展中国家而言则是挑战,Lee[1]基于1975—2001年间18个发展中国家的面板数据研究发现,不论长期或短期能源消耗均是GDP增长的影响因素,反之则不然,能源节约可能短期或长期的抑制发展中国家的经济增长。能耗尤其是工业能耗的高效利用至关重要,相关研究提供了依据,Pao[2]的研究显示,除俄罗斯外的金砖四国为了减少碳排放且不影响经济增长,增加能源供应投资和提高能源利用效率,并加强节能政策,以减少不必要的能源浪费。就我国而言,杜祥琬等[3]提出如按假设的低碳情景发展,2020年后我国经济增长与能源消费开始呈现逐步解耦的趋势,我国煤炭和石油消费量在2030年前达到峰值,且经济增长与高碳能源(煤炭和石油)消费也将在2030年前解耦,至2050年我国经济发展与能源消费接近绝对解耦。查建平等[4]认为促进工业经济与能源消费脱钩措施的重点方向是在进一步提升能效技术的基础上,着力推进工业产业结构升级的步伐,提升新型低碳能源的结构比重,改善能源的生产和消费结构。
水资源在生产活动中作为重要的生产要素,其高效节约地使用也越来越重要,用水效率低下阻碍了经济的发展[5],保障我国经济可持续发展的重点之一是提高工业水污染日渐严重背景下的工业用水效率[6],同时一个地区经济发展水平的高低也会影响该地区的用水效率[7]。姜蓓蕾等[8]认为工业用水具有用量大、用水集中、污染明显等特征,其用水效率也受到诸多因素的影响,如水资源条件、高耗水行业的比重、工业中科技投入程度和技术进步等。李静和任继达[9]的研究发现,工业化占比对工业用水效率有正向作用,而用水规模对用水效率有负向作用。张兵兵和沈满洪[10]研究认为工业水资源利用与工业经济增长和工业产业结构变化之间存在着长期均衡关系,且分别存在双向因果关系。雷玉桃等[11]提出,应通过提高节水意识和节水技术、鼓励循环用水、调整产业布局和优化工业结构,以及根据区域差异制定有区别的管理方案和制度等途径提高工业用水效率。
能源和水资源之间的资源配置及耦合对于发展集约高效的工业经济和建设生态文明具有重要作用。但是,目前并未普遍认识到工业能源和水资源之间的重要关系,对能-水的关注多数集中在与能源行业相关的水资源问题上,集中在煤炭行业上。孔令斯等[12]在技术层面关注如何解决我国水资源与能源之间发展不协调关系等问题;从全球能源贸易的角度,钟锐等[13]选取1992—2010年间217个国家和地区的能源数据,计算出能源国际贸易中的能源隐含水净流动量,证明了能源与水资源两者之间有紧密联系并且互相影响。
对经济、能源与水资源三者关系的关注相对较少。薛婧妍和刘耕源[14]明晰了“耦合”的三种应用情景及相应定义表述,从物理耦合及政策效果耦合视角进行能—水—食物—土地—气候变化五系统两两之间进行分析总结,结论显示城市中水系统和能源系统两者之间相互依赖,具有很强的关联性,与水系统有关的决策会对能源系统产生直接或间接的影响,反之亦然。马海良、李倩和庞庆华[15]的研究表明2005—2016年间经济发展与两种资源之间的脱钩关系更为明显,且其发展更为协调;而水资源和能源之间的脱钩关系与此相比有一定差距,但是从时间趋势角度来看,这种协调关系正在进一步加强。
总结文献可以发现,能源和水资源密切联系且相互影响,在工业经济领域尤其突出。众多国内外学者关注了水资源消耗与经济发展或能源消耗与经济发展的关系。从能-水互动角度关注能源和水资源利用及其与经济发展的关系,既能从新的角度衡量能源和资源等生产要素的利用效率,也能体现资源能源协调可持续发展;既促进经济增长,也符合建设生态文明的理念,这也正是本研究的出发点。
三、研究方法与数据
(一)相关指标
本文通过工业用能强度、工业用水强度指标衡量能源和水资源消耗程度,分别记为IE和IW,计算公式为:
(1)
(2)
式(1)(2)中,INDW为工业用水量/亿m3;INDE为工业能源消费量(标准煤)/万t;IGDP为工业总产值/亿元。
从式(1)和(2)可以看出,工业用能强度和工业用水强度分别反映在工业生产过程中能源和水资源所创造的经济价值。此外,为了刻画工业能源消耗和工业用水之间的关系,定义工业能源耗水系数,记为WE,计算公式为:
(3)
代入式(1)和式(2)得出:
(4)
式(3)用来表示工业领域生产单位经济价值的产品所消耗的水资源和能源比例,从式(4)的表达可以看出,能源耗水系数即是工业领域单位能源消耗所对应的水资源消耗的量,可以反映工业能源消耗和水资源消耗的脱钩状况。
(二)空间自相关方法
莫兰指数是用来度量空间相关性的一个重要指标,分为全局莫兰指数(I)和局部莫兰指数(Ii)。
1.全局莫兰指数
全局莫兰指数用来描述整个研究区域上所有空间单元之间的平均关联程度的指标,公式为:
(5)
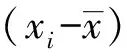
(6)
全局莫兰指数的取值为[-1,1],I越接近1表示区域间的正相关程度越强;越接近-1,表示区域间的负相关程度越强;接近0表示区域之间不存在空间自相关性。此外,可以通过服从标准正态分布的Z统计量判断空间相关性的显著程度。其中,
(7)
其中,E[I]=-1/(n-1),V[I]=E[I2]-E[I]2。
2.局部莫兰指数
局部莫兰指数可以体现空间位置不同时可能存在的不同空间关联模式,以体现局部空间的不稳定性,发现研究区域属性的空间异质特性,表示为:
(8)
若Ii为正,表示区域i与其临近区域存在相似的空间聚集,均为高值区时属于高高(H-H)聚集,或者均为低值区时属于低低(L-L)聚集。若Ii为负,表示区域i与其临近区域的属性值成负相关,即区域i存在相异值的空间聚集,区域i为高值则其邻近区域为低,反之亦然。
(三)面板向量自回归模型
面板向量自回归模型(PVAR)是采用面板数据拟合自回归模型(VAR),VAR模型是用模型中所有当期变量对所有变量的若干滞后变量进行回归,用来估计联合内生变量的动态关系,而不带任何事先约束条件。VAR(p)模型的数学表达是:
Yt=c+A1Yt-1+A2Yt-2+…+ApYt-p+εt,
t=1,2,…,N.
(9)
式中,Yt是k维内生变量向量;c是k维常数向量;εt是随机扰边项;p是滞后阶数;N为样本个数;k×k维矩阵A1,A2,…,Ap为待估计系数矩阵。应用VAR模型更多的是将其作为一个动态平衡系统,分析该系统受到某种冲击时系统中各个变量的动态变化,以及每一个冲击对内生变量变化的贡献度,即脉冲响应分析和方差分解分析。
(四)数据来源及变量说明
本文选取山西省11个地级市2005—2018年的面板数据。数据来源于各年份的《山西省统计年鉴》和公开发布的统计数据。研究中所涉及变量包括工业用水INDW,表示工业用水情况;工业用能INDE,由单位地区工业生产总值能源消耗与地区工业生产总值乘积计算而得;用工业生产者出厂价格指数(PPI)将名义工业生产总值调整为实际地区工业生产总值IGDP。
四、实证分析
(一)空间部分特征
工业用水、工业用能及工业生产总值的数据显示各年份各地区工业用水、用能及工业产值的绝对量。长期以来,高工业用能城市是临汾市、吕梁市和长治市,其中临汾市多年平均工业用能量最高;而阳泉市、忻州市和大同市多年来都是低工业用能城市,其中阳泉市各年平均能耗量最低,忻州市各年的工业用能量更为平稳。对工业用水而言,用水量较高城市是太原市、晋城市和长治市,其中太原市多年平均工业用水量最高,居于第一,而朔州市、忻州市、阳泉市多年来都是工业用水量较低的城市,其中朔州市多年的平均用水量最低,晋中市和临汾市各年的工业用水量保持相对平稳。对工业总产值而言,总产值较高的城市是太原市、长治市和吕梁市,其中太原市各年平均工业生产总值最高,工业生产总值低的城市是忻州市和阳泉市,其中忻州市多年平均工业生产总值最低。总体来说,2005—2018年,山西各市的工业生产总值呈现向上增长的趋势,其中2005—2009年上升趋势较为平缓,2009—2014年上升趋势变得剧烈,而2014—2015年各市的工业生产总值下降,在2015年之后山西各市的工业生产总值的趋势展现出不同的方向变化。表1所示为2005—2018年山西省各市平均的工业用能和用水情况。
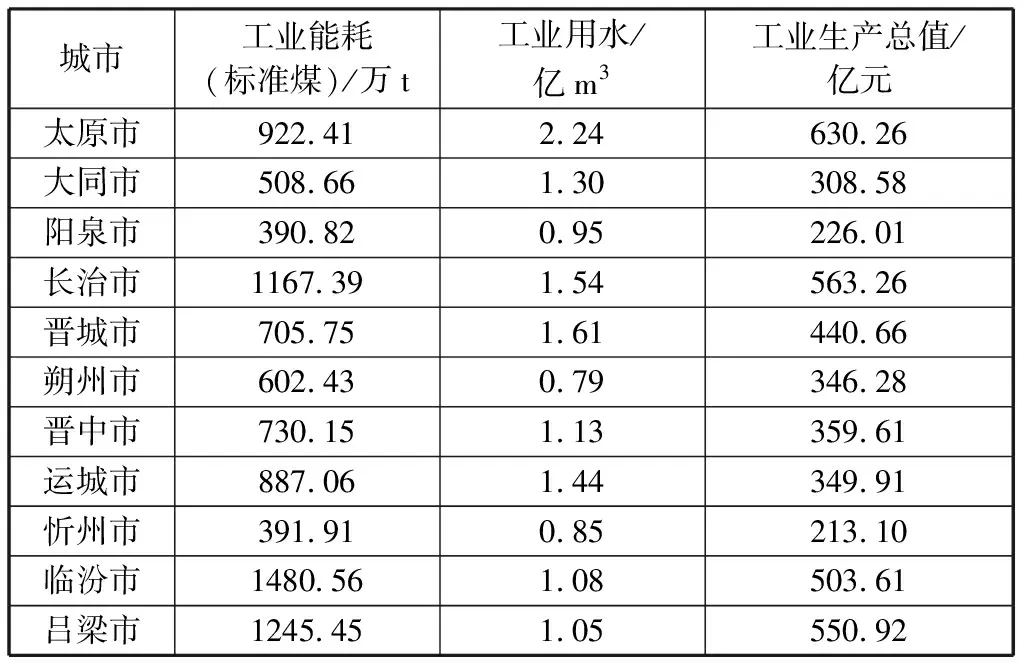
表1 2005—2018年山西省各市平均的工业用能和用水情况
工业用能强度、用水强度及能源耗水系数反映能源和水资源的相对消耗。工业用水强度、用能强度越高,说明创造单位工业产值消耗的能源和水资源越多;单位能源、水资源创造的工业产值越低,表示水资源、能源的利用效率相对低下。在本文研究的时间段内,高用能强度城市是临汾市、运城市和吕梁市,其中临汾市各年的平均用能强度最高;低用能强度城市是太原市、大同市和晋城市,其中太原市多年平均用能强度最低;各市的用能强度总体逐年下降。高用水强度城市是忻州市、阳泉市和大同市,其中忻州市多年的平均用水强度最高;低用水强度城市是临汾市和吕梁市,其中临汾市各年平均用水强度最低;各市的用水强度总体均有降低的趋势,其中2010年前下降趋势明显,之后趋势明显放缓。能源耗水系数表示单位能源消耗所对应的水资源消耗的量,反映工业生产中能源与水资源消耗的相对数量关系。能源耗水系数高的城市是太原市、大同市和阳泉市,其中太原市各年平均能源耗水系数最高;能源耗水系数低的城市是临汾市和吕梁市,临汾市各年来平均能源耗水系数最低,且两市多年的能源耗水系数十分平稳;总体上,各市的能源耗水系数呈现了先降低后提高的过程。
太原市作为山西的省会城市工业生产总值在全省居首,其工业发展对能源依赖较低,用能强度全省最低,工业发展需要的工业用水绝对量全省最高,高能源耗水系数也印证了这一点;工业产值较高的长治市尽管用能和用水绝对量较高,但是其使用强度水平居中,可见其工业经济对能源和资源依赖并不严重;工业产值较高的吕梁市的工业用能绝对和相对量均较高,但用水强度低,能源耗水系数较低,因此工业发展对能源的依赖严重;忻州市和阳泉市作为工业产值较低的两个城市,其对能源和水资源的消耗也呈现出共同的特征,工业发展所需的能源和水资源消耗的绝对量均在全省处于较低水平,但用水强度均较高,因此其工业发展对水资源消耗严重;临汾市工业能源消耗绝对量和强度均为全省第一,而用水强度全省最低,工业发展对能源依赖严重。山西省其他城市如大同市工业用水强度高,用能强度低,属于水资源依赖型工业;运城市用能强度较高,属于高耗能型工业;而晋城市用能强度较低,属于低能耗型工业;晋中市、朔州市工业发展中对能源和水资源依赖在全省居中。
(二)空间自相关性分析
2010年12月13日经国务院同意,国家发展改革委员会正式批复设立山西省国家资源型经济转型综合配套改革试验区。为了更好地比较分析山西省资源型经济转型前后的发展情况,选取2006、2010、2018年作为时间节点,分别反映传统经济发展阶段、资源型经济转型时及资源型经济转型改革后的经济状况,计算分析山西省各市工业用水强度、用能强度和能源耗水系数的全局和局部莫兰指数。
1.全局空间自相关分析
全局莫兰指数反映各市相关指标总体的空间相关关系,其结果如表2所示。
表2中给出了全局莫兰指数、统计量Z及P值。2006年用能强度全局莫兰指数为负且不显著,表明空间聚集特征不明显;2010年和2018年指数变为正数,且到2018年指数在10%水平下显著,表明用能强度空间聚集程度增强。用水强度的全局莫兰指数呈现的变化趋势和用能强度相反。2006年用水强度全局莫兰指数为正且在10%水平下显著,表明城市间用水强度呈现了正向的空间聚集,即用水强度较高的城市相互接近,用水强度较低的城市相互接近;2010年和2018年全局莫兰指数及其Z值显示用水强度空间集聚程度显著减弱,且由2006年的正全局相关转变为负全局相关,即用水强度较高和用水强度较低的城市均分散分布。2006年能源耗水系数的全局莫兰指数在5%的水平下显著,且有正向的空间聚集,即能源耗水系数高的城市聚集,能源耗水系数较低的城市聚集,比用能强度和用水强度的聚集程度更强;2010年和2018年呈现了与用水强度的全局莫兰指数类似的变化趋势,聚集程度逐渐减弱甚至为负。

表2 全局莫兰指数及其统计量
2.局部莫兰指数分析
为了体现资源和能源消耗的城市间差异,本研究计算局部莫兰指数。从计算结果可以看出,空间关联类型分为五类:高-高聚集、低-低聚集、高-低聚集、低-高聚集、不显著。其中,高-高聚集、低-低聚集表示正相关性;高-低聚集、低-高聚集表示负相关性。总体而言,不同时间点工业用水强度、用能强度、能源耗水系数的局部莫兰指数所显示的局部空间相关性在大部分城市中不显著,部分城市出现相似值聚集或相异值聚集。
工业用能强度的局部空间自相关结果如图1所示。2006年的低-高聚集区为晋城市,晋城市的用能强度低,而其周边城市临汾市、运城市和长治市的用能强度都较高。2010年低-高聚集仍然为晋城市,新增加高-高聚集区临汾市。2006—2010年,各市的用能强度均在减小,虽然临汾市及其周边的吕梁市、晋中市、长治市和运城市的用能强度也在下降,但其工业用能强度仍显著高于其他各市,而临汾市尤其突出。2018年高-高聚集和低-高聚集与2010年相比没有变化,新增了低-低聚集区阳泉市,因为阳泉市及其周边城市忻州、太原和晋中在2010年资源型经济转型试验改革的推动下,伴随着能源使用效率的提高,工业对能源依赖降低,工业用能强度在全省处于较低水平。
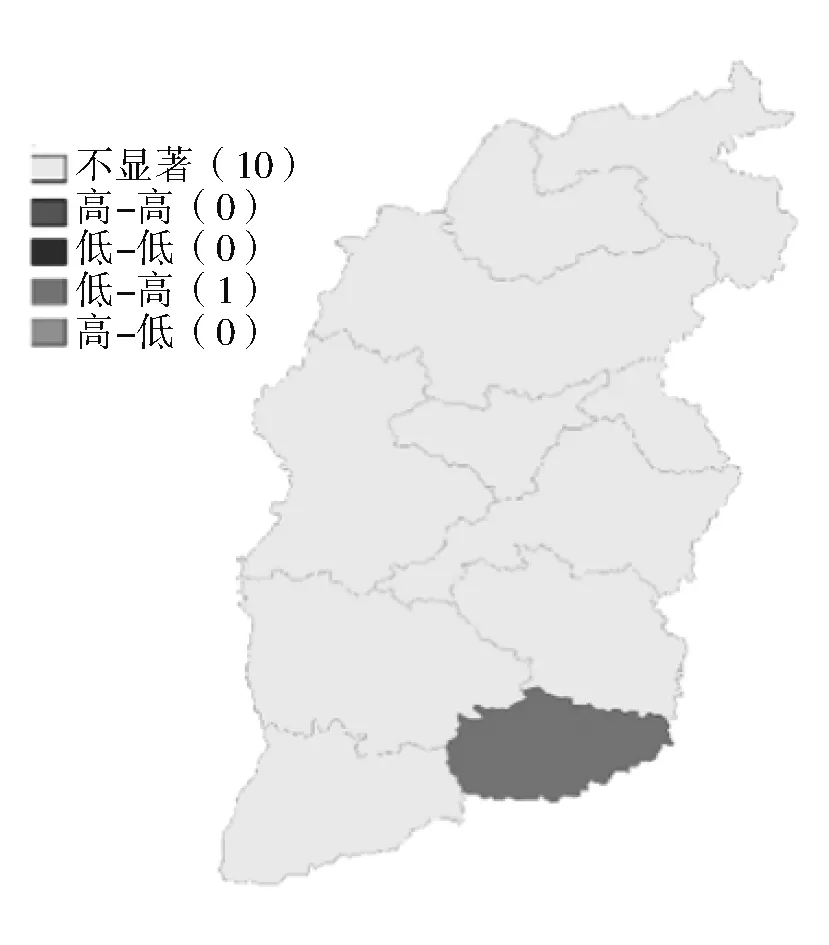
(a) 2006年用能强度空间自相关
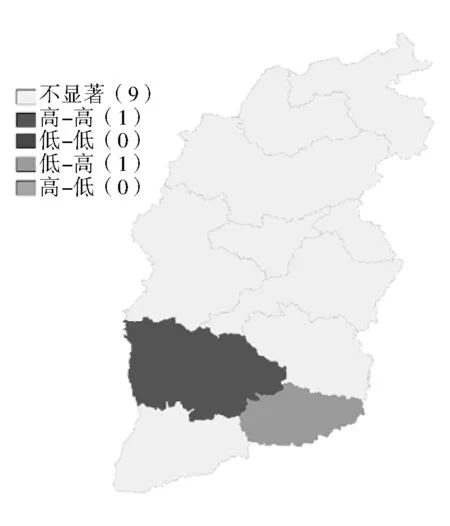
(b) 2010年用能强度空间自相关
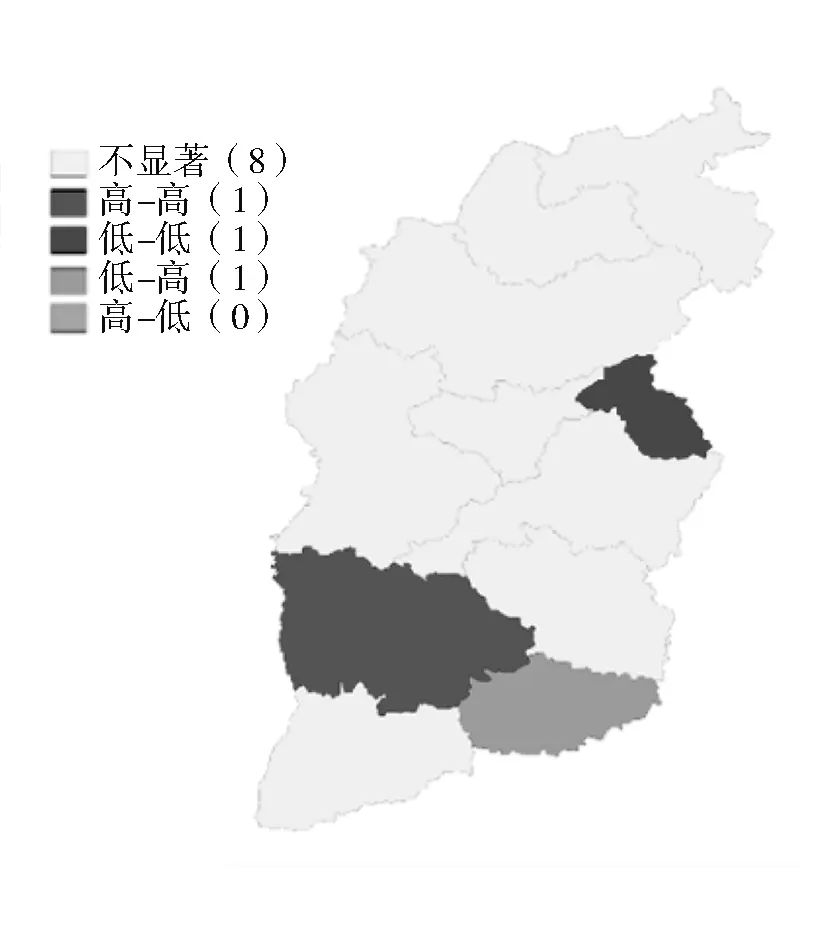
(c) 2018年用能强度空间自相关
工业用水强度的局部空间自相关结果如图2所示。2006年运城市、临汾市和长治市为低-低聚集区,这三个市的工业用水强度都低于其他城市;低-高聚集区仅有朔州市,朔州市的用水强度较低,而周边的大同市和忻州市的工业用水强度高。2010年低-低聚集区只有晋中市,原2006年的低-低聚集区和低-高聚集区变为不显著。2018年各市局部空间自相关均不显著,2010年的聚集区消失。结合各年份各城市的用水强度指标变化可以发现,随着时间的推移,各市的用水效率得到提高,用水强度显著下降,到2018年均处于较低水平,且各市间的差别较小,因此聚集性相较2006年减弱甚至消失。
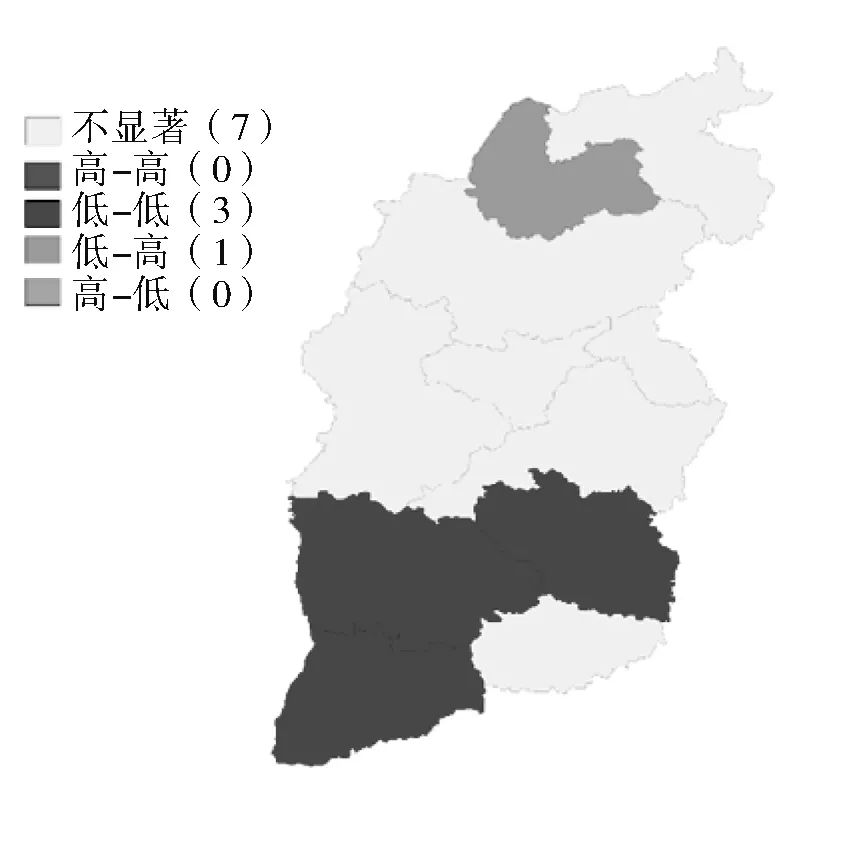
(a) 2006年用水强度局部空间自相关
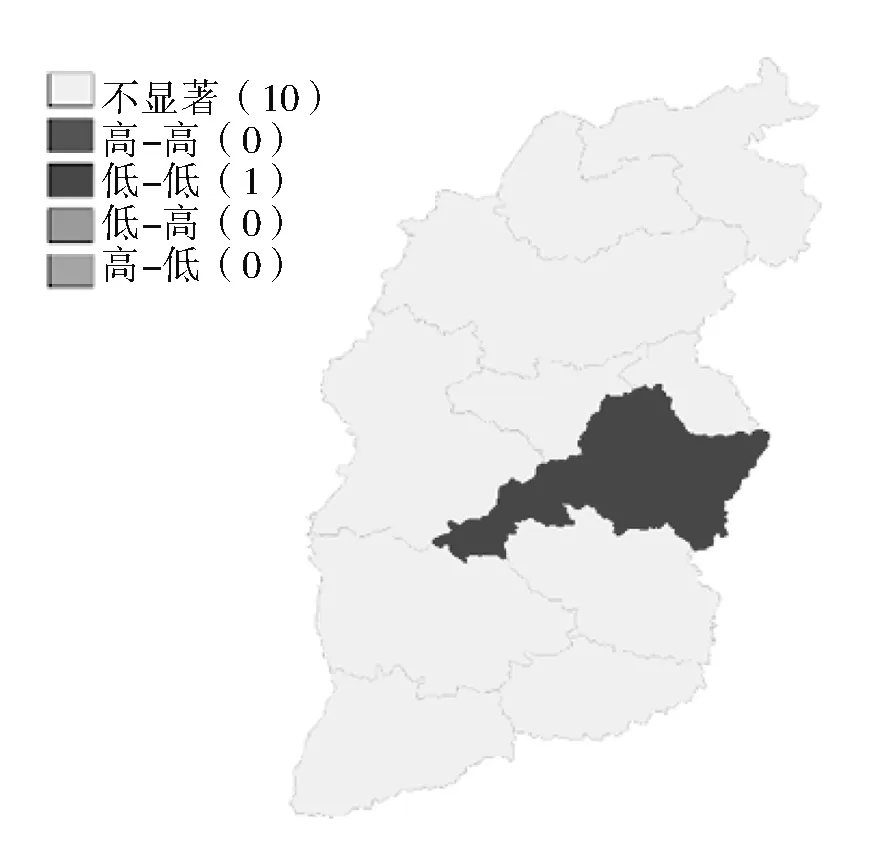
(b) 2010年用水强度局部空间自相关
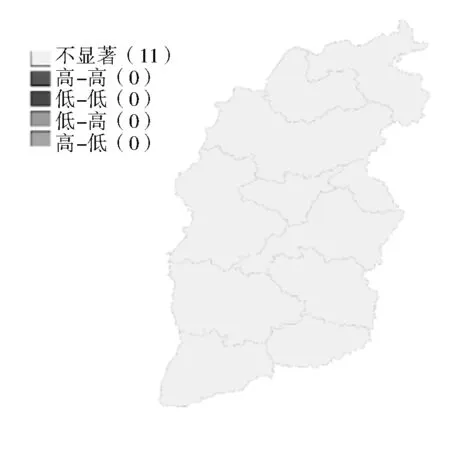
(c) 2018年用水强度局部空间自相关
工业能源耗水系数的局部空间自相关结果如图3所示。2006年低-低聚集区为临汾市、长治市和晋城市,表示工业能源和水资源消耗脱钩更明显,但是其原因不同,临汾市和长治市工业生产用能强度较大,而用水强度小,故能源耗水系数低;晋城市因为工业用水强度和工业用能强度都较小,但用水强度相对更小,故能源耗水系数低。到2010年,低-低聚集区与2006年相比少了长治市和晋城市,增加了晋中市,且晋城市变为高-低聚集区,临汾的能耗消耗结构和其2006年的类似,晋中市也是高用能强度、低用水强度,导致这两个城市比其周边城市具有更低的能耗系数。和2006年相比,2010年晋城市的用能强度和用水强度都有一定的下降,但是用能强度下降更加明显,导致能源耗水系数比周边城市的显著增高,形成了高-低聚集区。2018年,高-低聚集区晋城市变得不显著,低-低聚集区晋中市变得不显著,仅剩临汾市。临汾市仍然保持了和前两个时间节点一致的高用能强度、低用水强度的结构,保持了能源耗水系数低-低区聚集特征。晋中市用能强度下降程度更大,因此其能耗系数的低-低聚集区特征不再显著。晋城市用能强度和用水强度不同程度下降,导致能源耗水系数的变化,使其不再显著比周边城市更高。

(a) 2006年能源耗水系数空间自相关
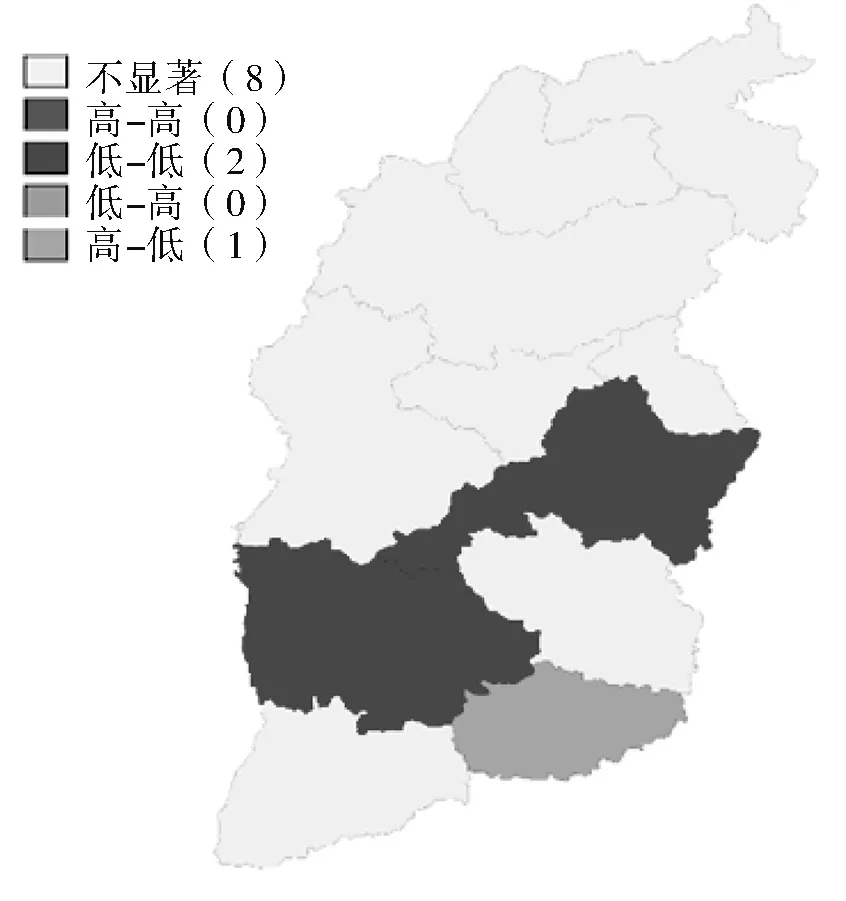
(b) 2010年能源耗水系数空间自相关
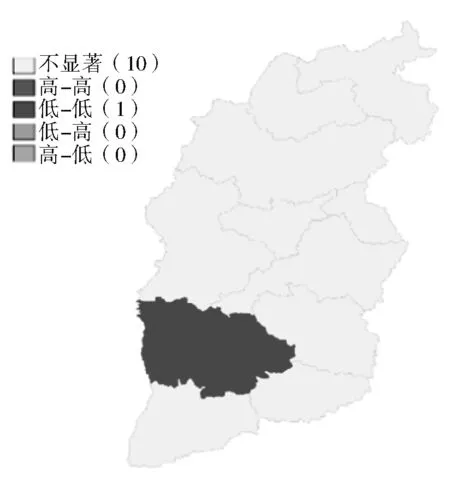
(c) 2018年能源耗水系数空间自相关
对比能源耗水系数的三个图形可以发现:临汾市的工业发展尽管能源水资源脱钩程度更大,但其建立在能源依赖的基础上,距离清洁低碳工业发展还有一定距离;长治市工业能源和水资源消耗强度下降使其能源耗水系数处于全省中等水平;晋中市能源耗水系数在2010年短暂地维持了低-低聚集区特征,其能源和资源消耗强度均逐渐下降,使能源耗水系数的空间聚集特征不明显;晋城市的工业发展显示了其低能耗和低水耗的特征,由于相对水平的变化导致其在2010年呈现了高-低聚集区特征,但也难掩盖其工业发展在全省更低碳可持续的特征;其他城市的能耗水系数空间聚集特征并不显著,但其能源和水资源消耗状况在上文用能强度和用水强度的分析中是明确的。
(三)基于面板向量自回归模型的工业能-水关系分析
建立PVAR模型,将工业用水量、工业用能量和工业生产总值三个变量纳入到一个系统中,通过格兰杰因果关系检验和脉冲响应分析三者动态关系,为消除异方差对变量进行对数处理。
1.单位根检验及面板VAR模型建立
针对面板数据的平稳性检验,本文通过IPS检验对三个变量序列的平稳性进行检验。由表3可得,lnINDW、lnINDE和lnIGDP的单位根检验统计量的P值明显大于0.1,即不显著,故原序列存在单位根,即是不平稳的序列;故对取差分后的序列DlnINDW、DlnINDE和DlnIGDP进行单位根检验,检验可见DlnINDW、DlnINDE的单位根检验统计量的P值均小于0.01,因此,在1%的显著性水平下拒绝原假设,而DlnIGDP可在10%水平下拒绝原假设,因此差分后序列不存在单位根,即数据平稳。
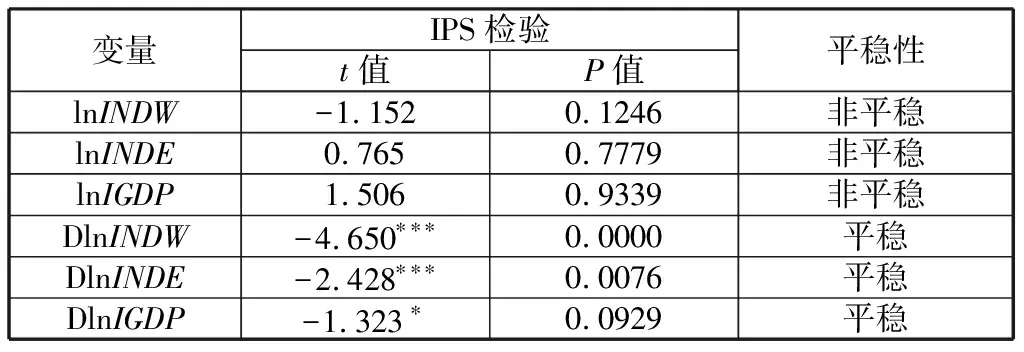
表3 单位根检验结果
由以上单位根检验可知序列均为I(1),通过LR、FPE和AIC标准所确定的最佳滞后阶数为2,因此建立滞后2阶的VAR模型,稳定性检验中所有AR特征多项式逆根都在单位圆内,回归残差满足正态性,不存在相关性和异方差,是平稳系统模型。利用KAO检验进行协整检验,其原假设是变量之间不存在协整关系。KAO检验统计量ADF对应P值为0.0704,因此在10%的显著性水平下拒绝原假设,即变量之间存在长期均衡关系。
2.格兰杰因果关系检验
在滞后2阶的VAR模型估计结果基础上,对变量进行格兰杰因果关系检验以揭示变量间的因果关系,结果如表4所示。
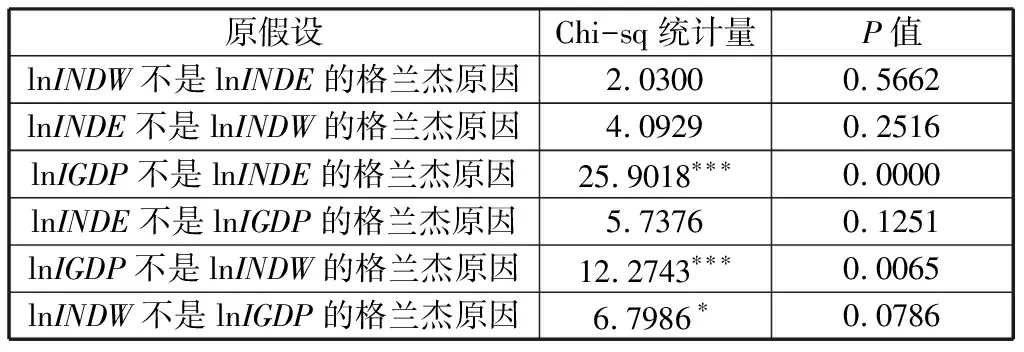
表4 格兰杰因果关系检验结果
在显著性水平为5%的情况下,工业生产总值是工业用水和工业用能的格兰杰原因,即工业生产总值会影响工业用水和工业用能;而在显著性水平为10%的情况下,可以认为工业用水是工业生产总值的格兰杰原因,即工业用水会影响工业生产总值;在显著性水平进一步放宽时,也可认为工业用能是工业产值的格兰杰原因;工业用能和工业用水之间没有直接的格兰杰因果关系,从时间维度上体现了工业用水和工业用能的脱钩。
3.脉冲响应
脉冲响应函数描述了来自某个随机扰动项的一个标准差冲击(称之为“脉冲”)对模型变量当期和未来期取值的影响,能形象地刻画出变量之间的动态作用的路径变化。根据格兰杰因果关系检验结果,本部分关注工业生产总值对工业用能和工业用水脉冲下的响应,以及工业生产总值脉冲下工业用能和工业用水的响应。
图4(a)和图4(b)分别为工业用能和工业用水对工业生产总值冲击的响应,实线表示脉冲响应函数,虚线表示正负2倍标准差偏离带。从图中可以看出,工业生产总值的冲击均会在短期内使工业用能和工业用水产生程度相当的正向偏离,之后再逐渐回归到原来的水平,工业用能回归的速度更快,所需时间更短,而工业用水这一过程更慢。因此,工业用水脉冲会导致工业用能和工业用水产生正向的响应,之后这种响应逐步变小,直至趋近于0。
图4(c)和图4(d)分别表示工业用能和工业用水冲击下工业生产总值的响应,可以看出工业用水和工业用能冲击下,工业生产总值不会同步做出响应,在第1期及以后响应才产生。工业生产总值对工业用能的冲击做出了先上升后下降的正向响应,之后响应程度逐步减小;而对工业用水的冲击做出了先正向后负向的响应,之后响应程度逐渐减小,而且后者减小的速度更明显。对比图4(a)、图4(b)和图4(c)、图4(d)可以发现,工业生产总值对工业用能和工业用水的冲击持续时间更短,而工业用水和工业用能对工业生产总值冲击持续时间更长。
图4(e)和图4(f)分别表示工业用水和工业用能受到外生冲击时对方的响应,工业用水冲击下工业用能产生负向的响应,呈现先增大后缓慢减小的趋势直至恢复到冲击前水平;工业用能冲击下工业用水在大部分时期产生负向的响应,并且在更短的时间内恢复到受冲击前的水平。
可以看出,工业生产总值的冲击导致了工业用能和工业用水产生正向的响应,之后逐渐回落到受冲击前水平,工业用能回落速度更快。当工业用能和工业用水受到冲击时,工业生产总值表现出不同的响应,前者受冲击时工业生产总值的响应是逐渐增大又变小的正向响应,而后者受冲击时工业生产总值的响应呈现出了先正后负的波动响应;此外,工业用能和工业用水冲击后,工业生产总值回落到受冲击前的水平需要更长的时间。工业用能和工业用水各自对对方脉冲的响应均表现出了负向的响应,并且响应持续的时间也近似。
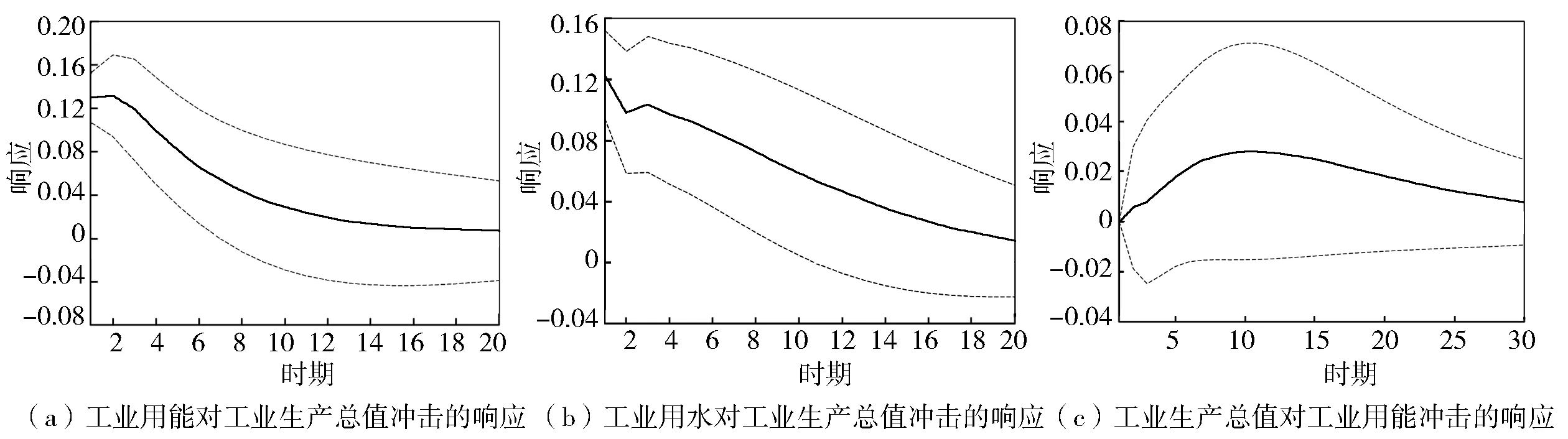
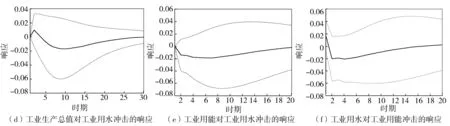
图4 工业生产总值、工业用能、工业用水各变量脉冲响应函数
五、结论与建议
根据以上研究内容,得出如下结论。
(1)山西省工业用能和工业用水强度表现出明显的地区差异,总体均呈现下降趋势;能源耗水呈现的地区差异和波动趋势揭示了工业能水的依赖关系。
(2)全局莫兰指数显示综合改革配套试验区建设使得工业用能的空间聚集程度增强,即工业用能强度较高的城市相互接近,工业用能强度较低的城市相互接近;同时工业用水的空间聚集程度减弱,即用水强度较高的城市、用水强度较低城市分散分布;能源耗水系数的空间聚集呈现了和工业用能相似的变化趋势,可见对能水依赖地区分化明显。
(3)局部莫兰指数显示综合改革配套试验区的建设使工业用能强度局部聚集特点呈现出地区差异;局部莫兰指数显示工业用水强度随着综合改革试验区的建设推进,局部聚集区逐步消失;局部莫兰指数显示工业能源耗水系数聚集性较弱,表明相邻地市的能水依赖关系存在一定差异。
(4)能水动态关系中,工业生产总值是工业用能和工业用水的格兰杰原因,工业用水也是工业生产总值的格兰杰原因;工业用能和工业用水并没有表现出因果关系;脉冲响应显示工业用能和工业用水在工业总产值冲击后立即产生正向的响应,随后逐步恢复到原来的水平;而工业用能和工业用水的冲击对工业生产总值造成的影响更加复杂,影响的时间持续更长;工业用能和工业用水各自对对方脉冲的响应均表现出了负向的响应,并且响应持续的时间也近似。
针对以上研究结论,提出如下建议。
(1)工业经济发展既要转变能源结构,水资源集约化使用也亟须关注,改变传统的能水依赖关系,实现工业能水脱钩是新型工业化的必由之路。
(2)资源型地区综合改革配套试验区的建设应持续关注经济转型的地区差异,进一步减少工业用能和用水的空间关联与聚集。
(3)避免工业经济、工业用能和用水的外生冲击,才能保证工业经济平稳发展,实现工业能水的高效利用。

