摆角受限条件下运载火箭起控技术研究

纪 刚，史丽楠，伊 鑫，窦志红，王 飞

（北京航天自动控制研究所，北京，100854）

0 引 言

运载火箭在飞行过程中，根据时序指令完成多次分离、转级和起控动作，起控动作是液体运载火箭贮箱晃动的激励因素，液体晃动抑制不好，不仅对箭体造成结构性破坏，而且与刚体运动、弹性振动相互耦合，造成姿控系统失灵。液体大幅度晃动同时对姿态控制系统的稳定裕度也会产生不利影响，起控平稳性在一定程度上决定了后续飞行的安全性。姿态快速收敛，可以使火箭速度方向尽快指向理论方向，减少燃料的消耗。在特定情况下，运载火箭起控面临箭体角速度60 (°)/s，姿态角偏差最大180°的极端工况。由于发动机摆角严格限制，控制能力受到极大约束，常规的PD 控制律会导致起控过程中出现发动机摆角长时间饱和，姿态稳定性和动态过程差的问题，液体火箭因此可能出现液体晃动不稳，动力系统燃料耗尽误判等情况。

为了解决这一问题，需要对起控过程协调设计，使得有限控制能力最优化使用。最优控制是现代控制理论的一个重要组成部分，20 世纪80 年代，Junkins和Turner就已经将最优控制理论应用到航天器姿态控制中。最优控制即为对给定系统，选取特定的控制输入，使得指定的性能指标函数达到最大或最小的一种控制。现代的最优控制方法，主要来源于动态规划和极小值原理两种理论。航天器控制的执行机构一般采用姿控喷管或者力矩陀螺，最优控制的方法有较多的应用探索，而运载火箭由于飞行中存在强非线性和高动态的特征，同时对于快速性和稳定性提出了较高的要求，新一代运载火箭更是对火箭适应能力提出了更高的要求。

本文在典型运载火箭主动段动力学模型分析的基础上，对控制能力受限条件下时间最优的姿态稳定控制问题进行了研究。

1 运载火箭动力学模型

1.1 运载火箭主动段动力学模型

考虑运载火箭弹性运动和液体晃动，为便于起控设计分析，以俯仰通道为例，基于系数冻结法和小扰动线性化假设的小偏差方程，并且不考虑弹道倾角的长周期运动和大气的影响，简化后的动力学方程为

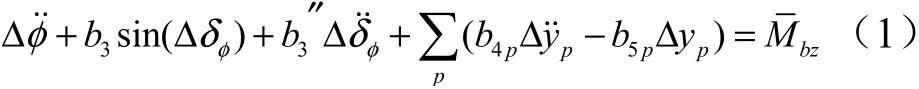
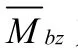
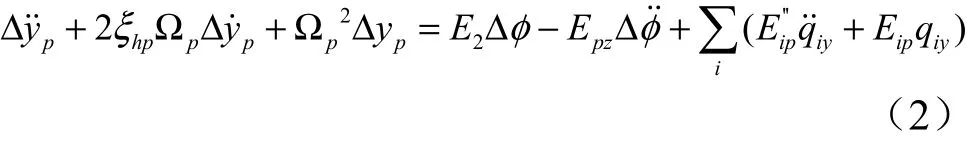
式中 Δy为第阶晃动的广义位移；Δ˙˙为第阶晃动的加速度。

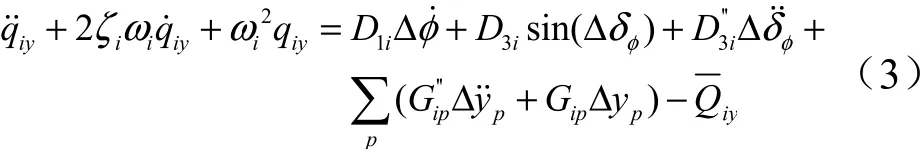
式中为第阶弹性的广义位移；为广义法向方向的广义干扰。

简化后的动力学方程实践中可以被用于进行火箭姿态控制系统分析设计。

1.2 姿态控制方程

以角偏差作为控制的主要指标，采用PD 调整参数，形成控制指令并对其进行分配，驱动伺服机构进行运动，实现箭体姿态对理论程序角的跟踪，控制系统如图1 所示。

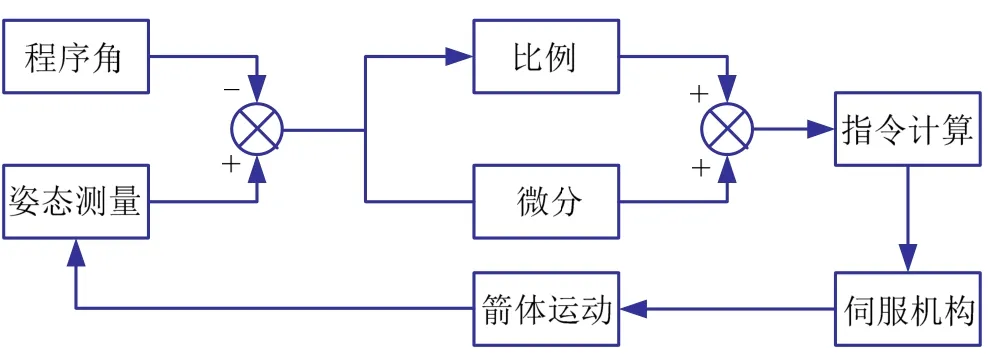
图1 姿态控制系统原理Fig.1 Principle of Attitude Control System

运载火箭因其动态高，参数时变性强的特征，经常采用简单可靠的PD 控制，还可以借用速率陀螺等测量设备降低姿控系统稳定性设计的难度。运载火箭PD姿态控制的根本是系统的角偏差，其基本原理是对角偏差进行比例、微分控制，通过对这两个环节系数进行设计调节，结合箭体传递函数，使系统满足古尔维茨稳定性定律，得到如下的控制方程：

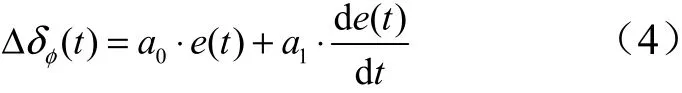
传递函数表达式为

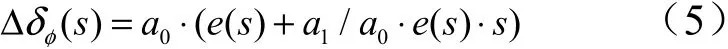
式中为发动机摆角与角偏差的比例系数；为发动机摆角与角速度的比例系数。

比例系数约定了角偏差与控制摆角的比例关系，在满足稳定性要求的条件下，可以加快系统的响应速度，但过大的比例系数会引发系统的振荡，严重影响系统的稳态性能。微分系数可以有效地对系统提供超前相位，但过大的微分系数会对角偏差中的特定频率进行放大，出现不合理的指令振荡，系统稳定裕度下降，控制品质受到影响。

从式（5）可以看出，控制摆角Δ 在常规的应用中，遵循了箭体角偏差和角速度/的指令分配关系，但在恶劣的起控阶段，大的角偏差和大的角速度会“争抢”有限总摆角Δ ，导致发动机摆角无序分配，且长时间饱和，角偏差和角速度也会剧烈振荡，系统长时间处于不稳定状态。

另外从式（1）至式（3）可以看出，晃动运动与姿态运动存在强的关联性和耦合性。1969 年ATS-V 航天器和2000 年NEAR 航天器的失效以及2007 年SpaceX 运载火箭发射失败均是由贮箱内液体燃料晃动所导致的。抑制晃动干扰的控制方法有很多，除在贮箱内增加防晃板等措施外，确保姿态运动的平稳是一个必要的条件。

2 控制能力受限的起控问题

2.1 最优起控问题描述

火箭起控过程，重点在于刚体运动部分角偏差和角速度综合求解，对于晃动、弹性部分的描述可以暂不考虑，且由于控制能力远大于结构干扰，δΔ 较小的条件下，式（1）可表达为

时间最短问题的提法可以表示为

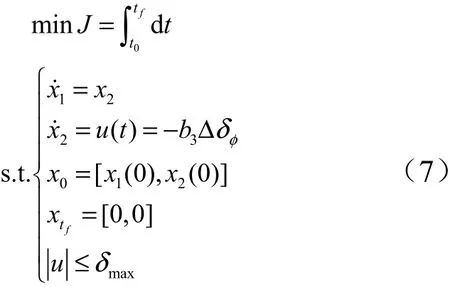
式（7）写为状态方程为

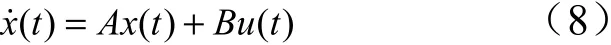
由此可以得到哈密尔顿函数为

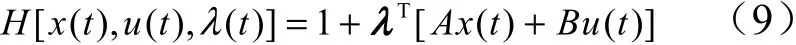
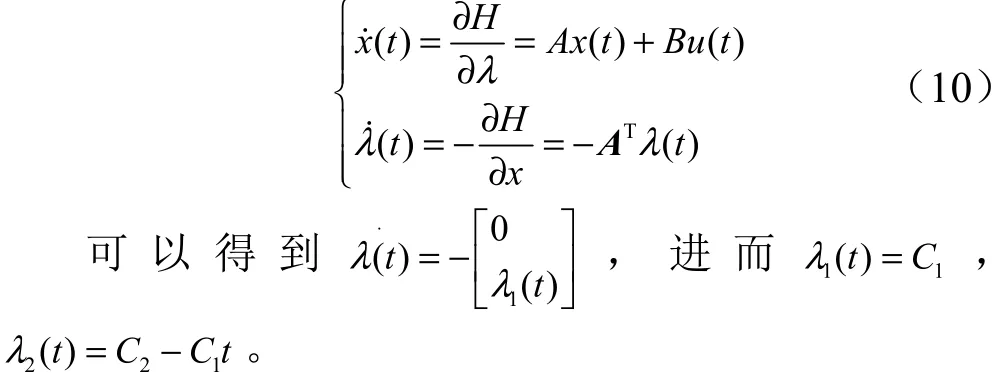
由全局最小，应有，当() > 0，取() < 0，当() < 0，取() > 0。

运载火箭控制量() 通过摆动发动机产生的摆角Δ 实现对火箭的控制，求解后有：

进而得到：

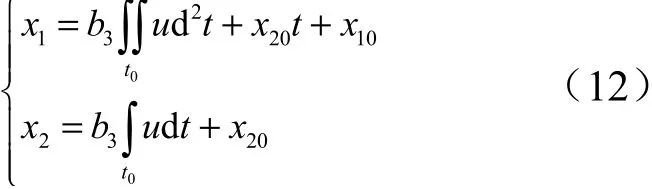
由式（12）可以看出，当控制量是一个大小恒定的数值，时间最优的控制实际上表现为是一族与时间相关的抛物线，如图2 所示，其中给出了、和3 条曲线开口向左、控制量为负值的情况，每条曲线的顶点代表不同的起控初始条件。

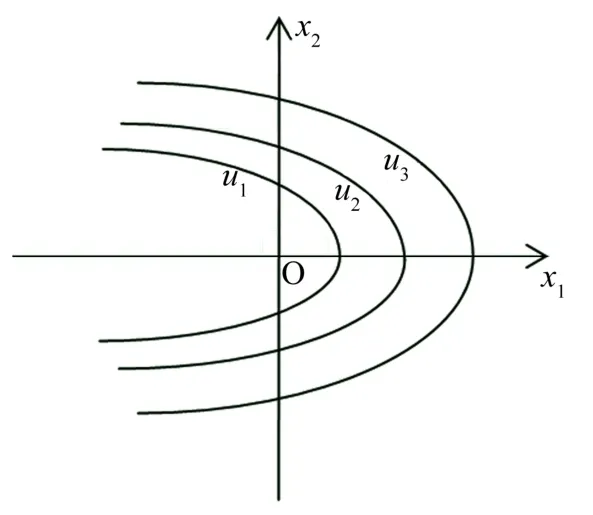
图2 状态变化规律Fig.2 Law of State Change

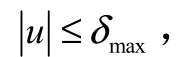
2.2 运载火箭最优控制推导

实际负反馈控制中，控制量与比例关系，不能简单地考虑为一个恒定数值，则式（12）可表示为

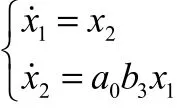
求解后得到：

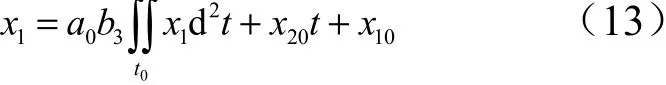
由式（13）可以看出，建立了控制量与比例关系后，变化趋势是运动初始状态、控制时间、静态增益与控制力矩系数之间的关系。考虑系统稳定性，采用式（5）建立与的关系后，式（13）的表达形式则变为

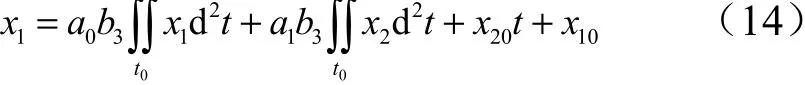
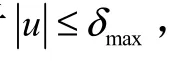
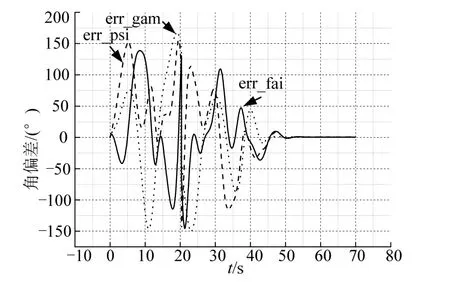
图3 姿态角偏差Fig.3 Attitude Angle Deviation

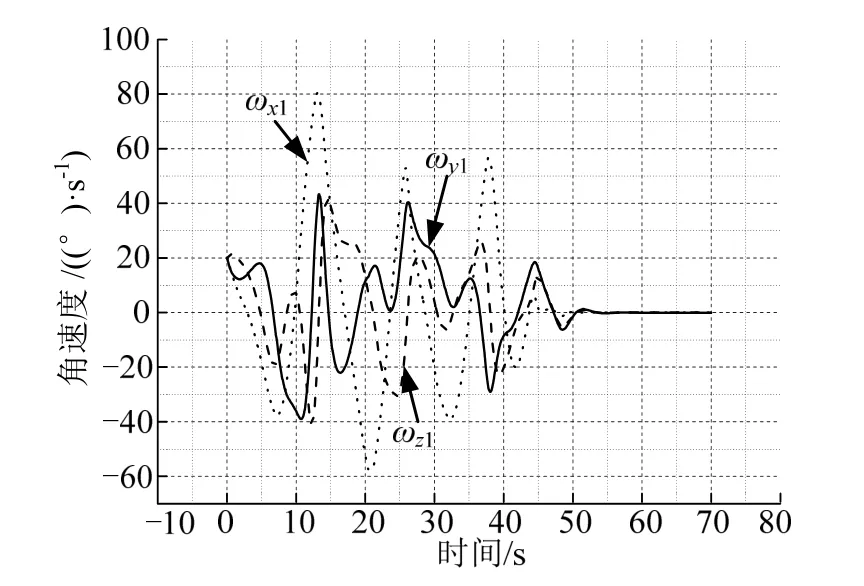
图4 姿态角速度Fig.4 Attitude Angular Velocity

图3至图5 的起控过程，即便火箭姿态最终实现了稳定，但动态过程会对火箭贮箱液体晃动运动造成不利影响，液位传感器可能会被误触发导致灾难性后果。另外，在杆臂效应下，对火箭箭上产品也会产生不利的影响。

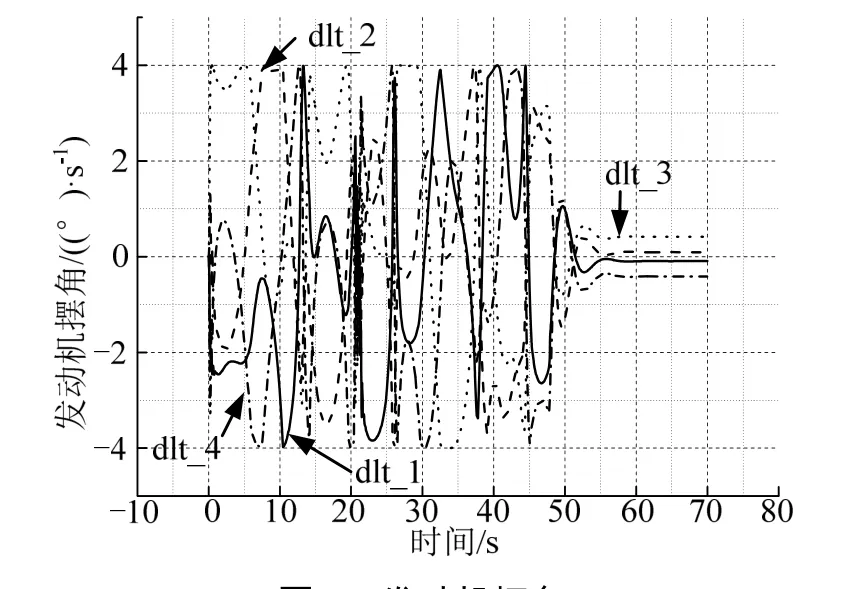
图5 发动机摆角Fig.5 Engine Swing Angle

2.3 滑模变结构控制律设计

运载火箭的发动机摆角受伺服机构产品设计和工艺的约束，不能实现任意摆角摆动，但在火箭转级转段过程中，火箭一般都会受到发动机后效干扰、分离冲击干扰的影响，前续飞行段残余控制偏差、非预期突发故障等都会对起控的平稳性和快速性带来巨大的影响。因此对多约束下时间最优的姿态控制技术应用显得极其迫切，但该技术方法目前多用于航天器等慢变姿态控制系统的时间最优机动问题中。伪谱法依然可以处理约束简单的时间最优机动问题，但是在火箭快速性、大动态和稳定性等多约束情况下的能力是有限的。滑模变结构控制具有响应速度快、对模型参数变化和外部扰动不灵敏、无需系统在线辨识、物理实现简单等优点，因而得到广泛的应用。

针对本文提出的运载火箭转级转段后，起控过程中面临大角速度和大姿态角偏差的极端工况，必须在发动机摆角小且严格受限的条件下，协调角速度和角偏差两种模式的逻辑处理，实现快速和稳定的起控。

从前文的分析可以看出，时间最优控制在工程实现中，由于摆角限制、箭体安全性等因素，难以工程应用实现。为了协调“争抢”摆角的问题，在最优化分析的基础上，进行变结构控制律的设计。变结构控制框图如图6 所示。

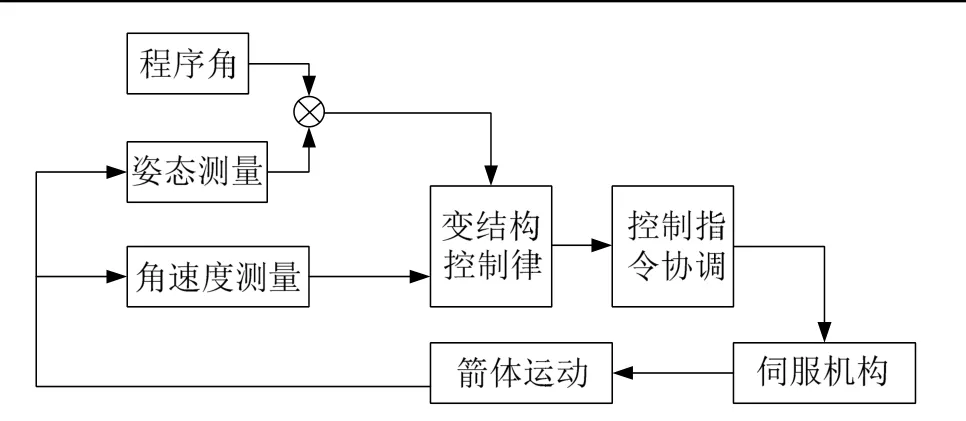
图6 变结构控制框图Fig.6 Variable Structure Control Block Diagram

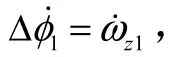
令切换函数为

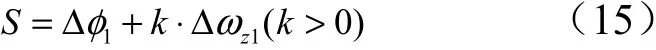
根据变结构滑动模态存在条件˙ <0 可以得到

考虑程序角变化，有：

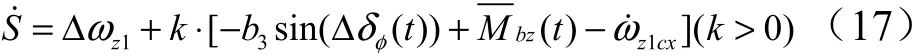
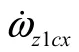
为简化分析，式（17）可以表示为

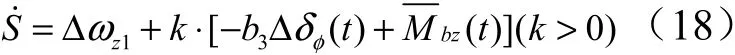
进而得到：

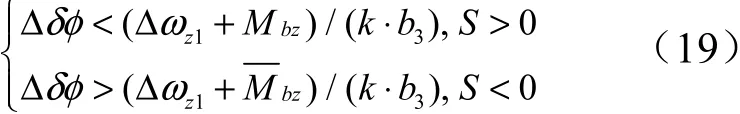
根据式（19）可以得到基于变结构的发动机摆角设计值，变结构控制存在固有缺点，抖振的问题需要考虑。 ()Δ 数值分别来源于姿态角偏差即 1Δ 和姿态角速度 z1Δ ，式（19）虽然能够解决时间最优控制所带来的指令耦合问题，但发动机摆角的限制带来的问题依然没有解决。结合火箭控制能力，设计协调控制项对摆角的限制进行处理。

设计协调控制项， sgn(Δ)，将其加入到控制指令之中，满足如下条件时进行控制。

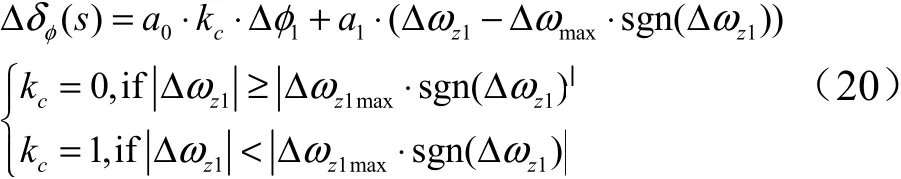
根据式（20），给出如图7 所示的火箭起控协调变结构控制逻辑框图，其中阈值条件需要根据火箭常规控制能力进行界定，一般要求Δ 不能长时间不满足发动机摆角的限幅要求。

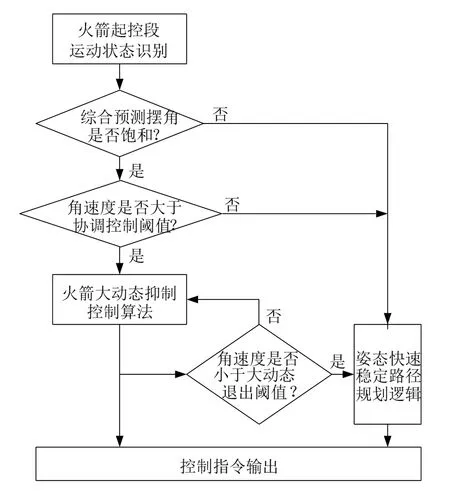
图7 变结构控制逻辑Fig.7 Variable Structure Control Logic

式（19）和（20）中可以看出变结构控制方法本身存在抖振问题，对于高动态飞行的运载火箭，不能随意进行控制律的切换，而本方法要做到的目标也是在实现一次控制律结构调整后，依然确保火箭稳定的跟踪弹道程序角，因此可以避免多次切换带来的抖振问题。

3 仿真结果及分析

采用前文所述的相同仿真用例，俯仰、偏航和滚动角速度均为20 (°)/s，角偏差分别为-178°，-70°，-178°时，系统长时间振荡难以稳定，姿态角偏差甚至达到了最大180°左右的情况。使用如图7 所示的控制变结构逻辑，角速度阈值采用8 (°)/s，仿真的结果如图8~10 所示。从图8、图9 可以看出，箭体角速度4.62 s 得到抑制，变结构策略介入后，姿态在20 s 附近即可进入角偏差较小的稳定状态。从图10 中发动机摆角的情况可以看出，除初始时刻摆角较大外，其他时间摆角均很小，相比图5 有很大改善，箭头所指为变结构控制切换点。

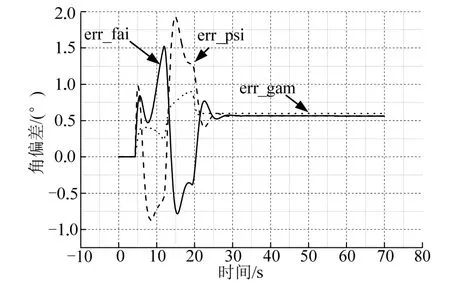
图8 姿态角偏差Fig.8 Attitude Angle deviation

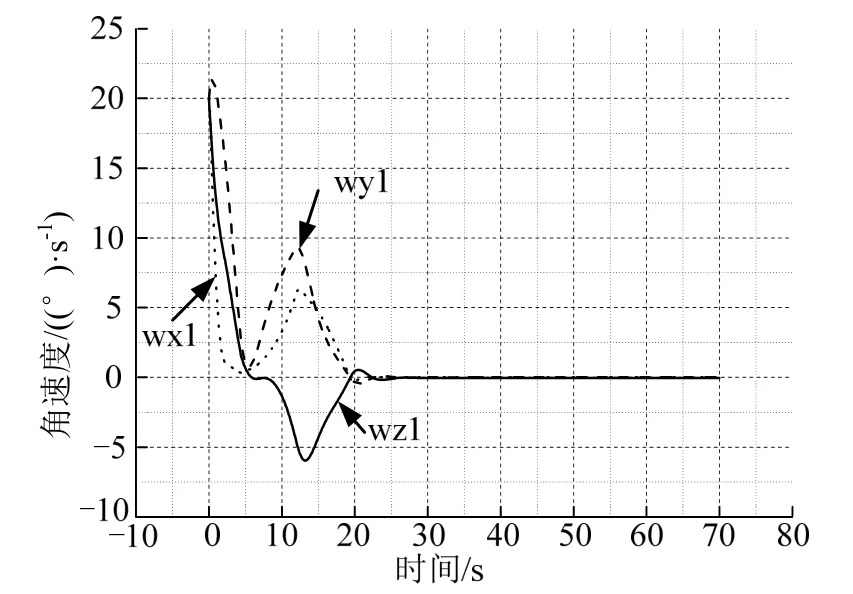
图9 姿态角速度Fig.9 Attitude Angular Velocity

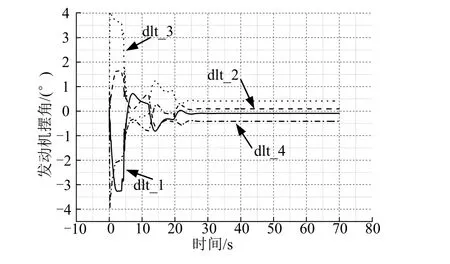
图10 发动机摆角Fig.10 Engine Swing Angle

4 结束语

本文提出了摆角受限条件下，协调角速度和角偏差的运载火箭起控段变结构控制方法。该方法针对运载火箭在转级转段过程中大姿态角偏差和大姿态角速度同时存在的特点，通过对时间最优控制问题进行研究，采用变结构控制策略实现姿态快速回稳的目标。通过仿真，结果表明，该方法可以有效地解决指令“争抢”问题，达到姿态稳定起控的目的。