摆动机构负载特性仿真分析与试验研究

2022-06-27 09:53郭洪波金建峰

导弹与航天运载技术 2022年3期

王姣，郭洪波，金建峰，刘宁，常远

（北京航天长征飞行器研究所，北京，100076）

0 引言

摆动机构作为一类特特殊的操纵系统，是机械结构设计中的一项重要内容和主要难点。首先，摆动机构运动情况复杂，给运动学分析及方案设计带来了较大的困难。此外，摆动机构承受着严酷的外部载荷作用，负载力矩较大，目前常用的操纵系统很难满足机构摆动所需的驱动力要求。而机构负载以摩擦负载和外部力矩负载为主，负载情况复杂，传力路径、结构变形等情况对负载特性影响较大，需要对摆动机构负载特性进行分析，为减小摆裙摆动机构运动的负载力矩提供依据。

本文基于对摆动机构复杂运动过程的分析，采用有限元软件ABAQUS，开展了摆动机构动力学仿真，揭示摆动机构的运动学和动力学特征，实现了对摆动机构负载特性的精细模拟，分析摆动速度、俯仰角、摩擦系数以及外部载荷对负载特性的影响，为机构负载特性优化提供思路。通过开展相关试验，研究摆动机构的负载特性及摩擦性能，验证仿真分析结果的有效性和优化方案的可行性，为这类操纵结构的设计提供技术和试验支持。

1 摆动机构结构形式及运动学分析

摆动机构由固定壳体与可活动机构组成，其结构如图1 所示。摆动机构通过控制作动器的伸缩实现操纵机构运动的目的。

图1 摆动机构结构示意Fig.1 Schematic Diagram of Swing Mechanics

摆动机构运动学分析时各结构都按刚体考虑。根据其运动特征，摆动机构以固定壳体的球心为中心点做定点运动，并通过经过球心的两个导向钮限制摆动机构的自转角度，从而实现俯仰和偏航两个方向的定点运动。

如图1 所示，为全局坐标系，其中轴沿过渡锥轴线方向。为便于描述机构运动，建立参考坐标系，新坐标系通过保持全局坐标系的轴不变，并绕旋转角度得到，显然1 轴与轴重合；建立随活动壳体运动的随体坐标系，使其轴与参考坐标系的轴重合，绕轴旋转角度w得到。

记空间任意一点在全局坐标系中的坐标为(,,)，在参考坐标系的坐标为(,,)，两者的转换关系为

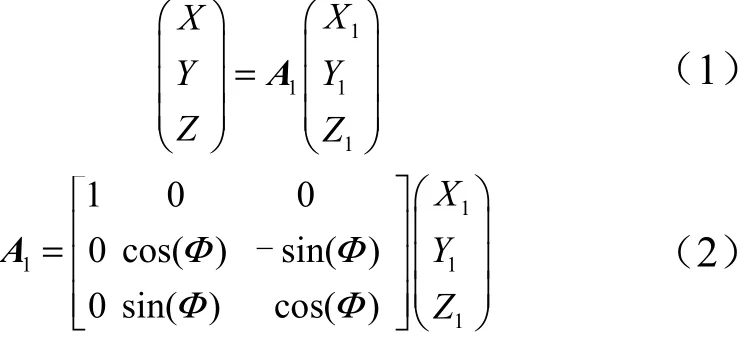
式中为摆动对称面与平面的夹角，称为摆动滚转角，其变化范围为[-90°，90°]；为机构的摆动角度，称为摆动偏转角，根据结构形式限定其范围为[-10°，10°]。

从而有：

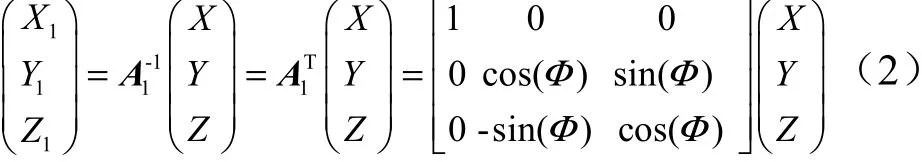
而空间任意一点在随体坐标系（坐标记为(,,)）和参考坐标系中的转换关系为

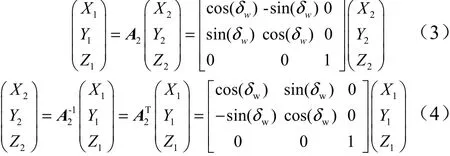
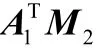
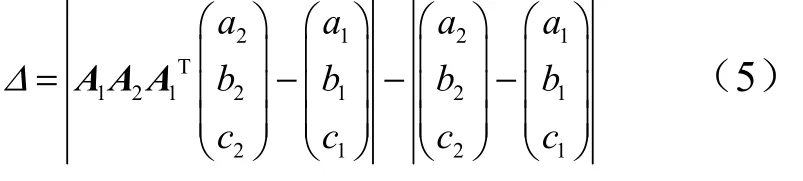
式中为负值时代表压缩，为正值代表拉伸，机构摆动过程中伸缩量的变化历程即为作动器的运动规律。

2 负载特性仿真分析

2.1 有限元计算模型

建立摆动机构有限元模型，使用C3D8R 单元划分网格，整个模型共包含213400 个实体单元；固定壳体与底座之间建立Tie 约束，与活动壳体之间建立接触关系，在底座大端施加固支约束；根据摆动机构表面压力分布，采用Analytical Field 节点Mapped 方式将其加载到摆动机构外表面，模拟摆动机构承受的外部载荷，为便于后文描述，记其使用状态下承受的载荷为使用载荷，并称计算中实际施加的外部载荷与使用载荷的比值为载荷系数；采用ABAQUS 中Connection单元的Translator 方式模拟伺服作动器连接，并将运动学分析所得的作动器的运动规律作为Translator 的输入条件，通过控制Translator 连接的轴向位移来模拟伺服作动器的运动情况。有限元计算模型如图2 所示。

图2 有限元计算模型Fig.2 Finite Element Calculation Model

2.2 负载特性分析

机构总负载力矩（主动力对固定壳体球心的矩）主要包括惯性力矩、外力负载力矩和摩擦力矩，由于惯性力矩通常为小量，因此在本文中不予考虑。负载特性分析的目的是通过有限元模拟揭示摆动机构的动力学过程，获得摆动机构的外力负载力矩、摩擦力矩及总负载力矩，进而研究机构负载特性的主要影响因素。

2.2.1 摆动速度对负载特性的影响

为了揭示摆动速度对机构负载特性的影响，取固定壳体与活动壳体之间接触面上的摩擦系数为0.1，考虑实际使用载荷下机构以10~80（°）/s 的平均速度，按俯仰方向±5°摆动的情形。图3 给出了机构以40（°）/s 的速度摆动时伺服作动器的运动规律及其作用力的变化趋势，其中作动器1、4 和作动器2、3分别位于摆动对称面的同一侧，呈X 字形分布。图3结果显示，作动器呈现周期性运动，摆动机构启动瞬时需经历由静到动的调整过程，对应的作动器驱动力为不规则波动，随后逐渐呈现出周期性变化趋势，本文只考虑进入稳定周期模式后的负载特性。

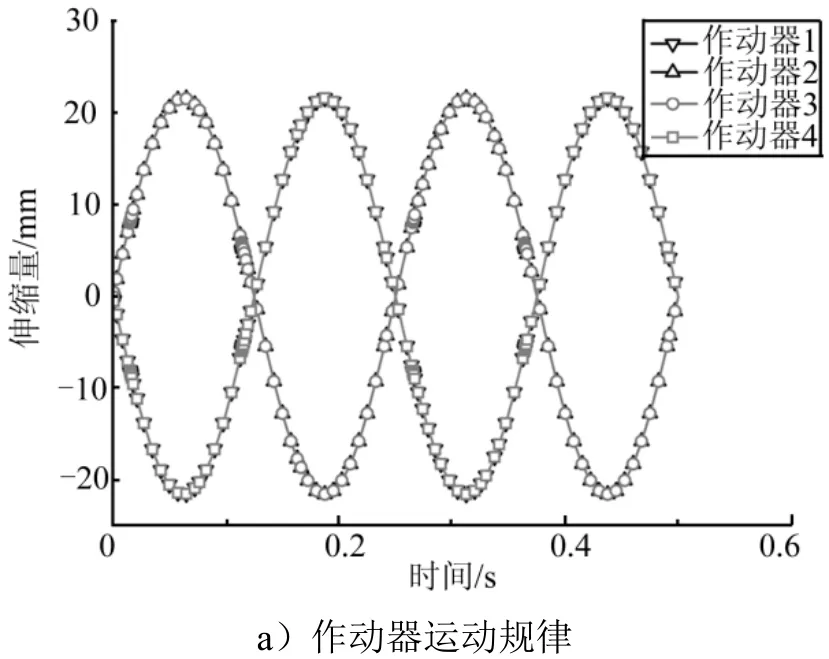
图3 作动器运动规律及其作用力变化规律Fig.3 The Motion of Actuator and Change Rule of Its Force

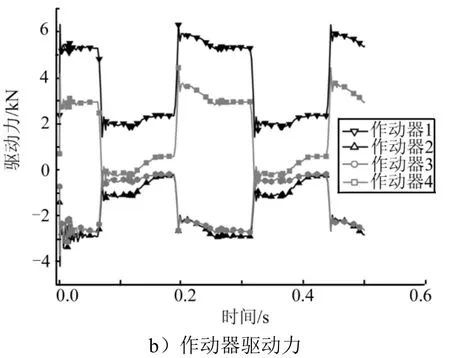
续图3

负载力矩随摆动速度的变化趋势如图4 所示。从图4 中可以看出，摆动速度对负载力矩有显著影响，随着摆动速度的加快各负载力矩均有明显地增加，且增幅随着摆动速度的增加逐渐增大。另外，不同速度下摩擦负载占总负载力矩的比例基本保持不变，约为40%~45%，这表明摩擦负载和外力负载相对摆动速度的变化率基本一致。

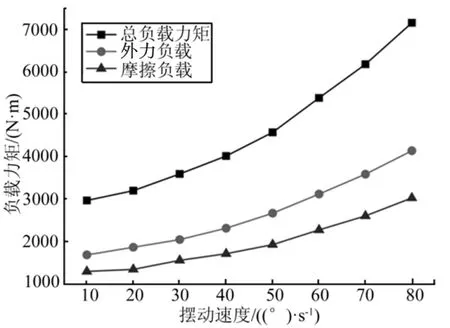
图4 负载力矩随摆动速度的变化趋势Fig.4 Change Trend of The Load Torque with Swing Rate

2.2.2 俯仰角对负载特性的影响

保持第3.2.1 节的其它条件不变，考虑机构以40（°）/s 的速度，分别按俯仰方向±2.5°、±5°、±7.5°、±10°运动的情形。计算所得不同俯仰情形下总负载力矩最大时刻的负载特性如表1 所示，可知负载特性基本受俯仰角度的影响不大。

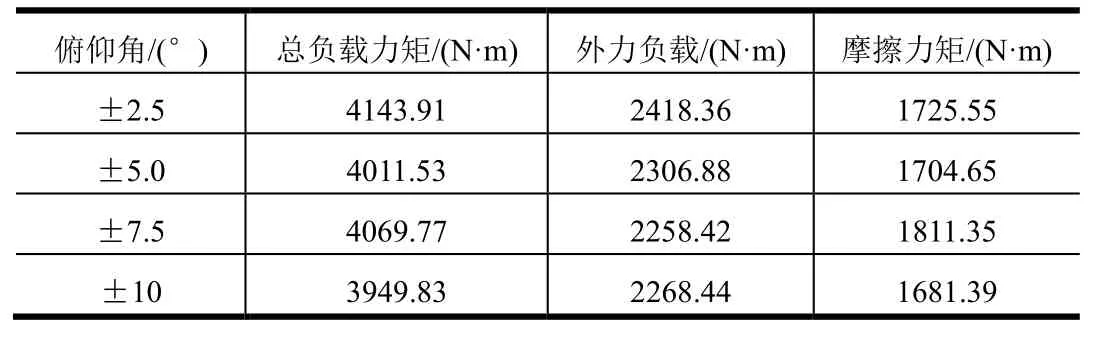
表1 不同俯仰角对应的负载力矩Tab.1 The Load Torque of Different Pitching Angle

2.2.3 外部载荷对负载特性的影响

外部载荷也是影响负载特性的一个重要因素，为了揭示负载力矩与外部载荷的关系，计算分析了机构以40（°）/s 的速度运动，载荷系数（即计算中施加载荷与实际使用载荷的比值为载荷系数）分别取0.5、1.0、1.5、2.0、2.5、3.0，其它条件与第2.2.1 节中的保持不变时的负载情况，结果如图5 所示。计算结果显示，各负载力矩均随载荷的增加逐渐增大，并与载荷系数近似呈线性关系；且不同载荷系数下，外力负载和摩擦力矩占总负载力矩的比例基本保持不变。

图5 负载力矩随载荷系数的变化趋势Fig.5 Change Trend of The Load Torque with Load Factor

2.2.4 摩擦系数对负载特性的影响

为了分析界面接触状况对机构负载力矩的影响，分析摩擦系数介于0.05~0.3 之间，俯仰方向为±5°时，机构在使用载荷下分别以20（°）/s、40（°）/s、60（°）/s 的速度摆动的情形。图6 分别为不同速度情形下总负载力矩、外力负载及摩擦力矩随摩擦系数的变化趋势。

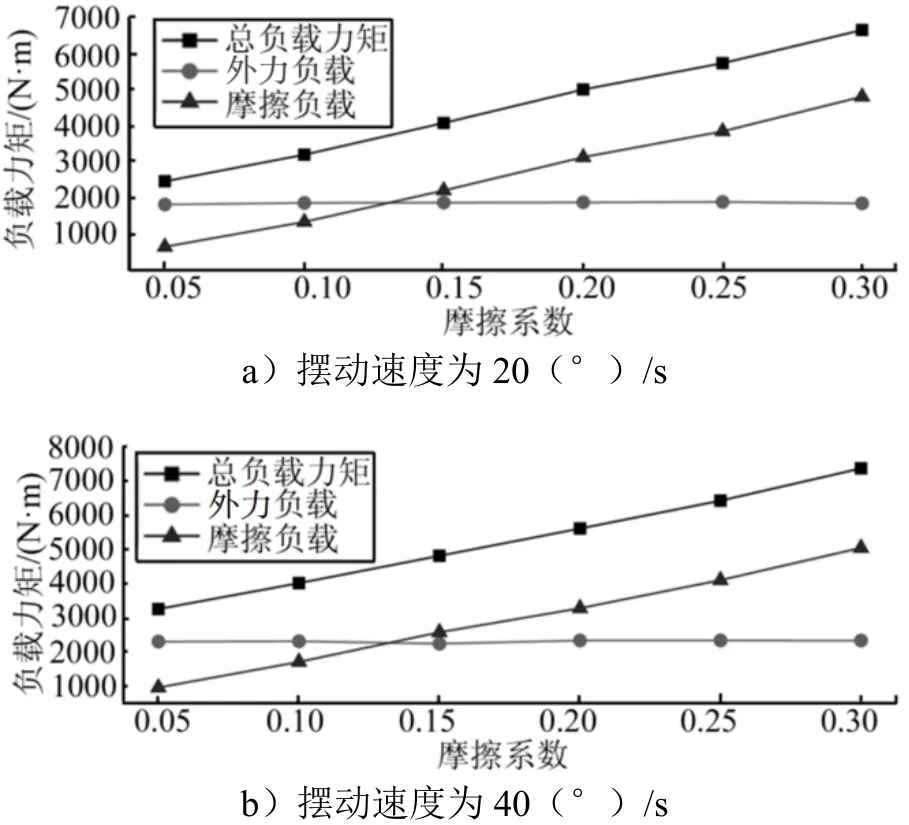
图6 负载力矩随摩擦系数的变化趋势Fig.6 Change Trend of The Load Torque with Coefficient of Friction

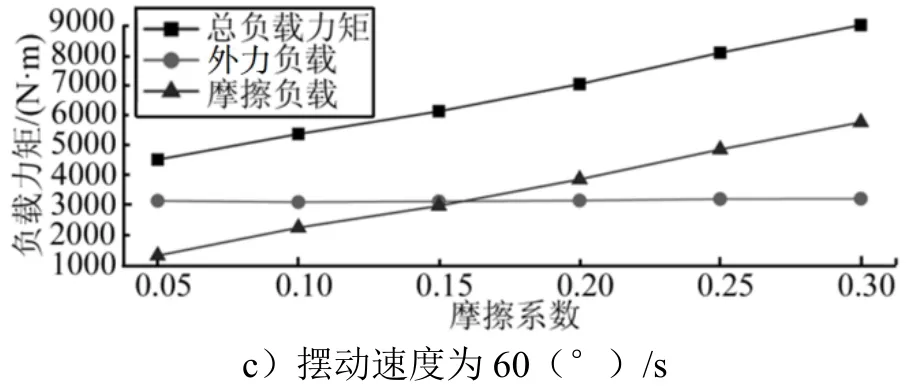
续图6

由图6 可知，总负载力矩随着摩擦系数的增加呈现出明显地上升趋势，且与摩擦系数近似为线性关系，这表明总负载力矩的变化主要依赖摩擦力矩的变化，而外力负载力矩则与界面接触状况无关。

从上述分析结果可知，摆动速度、外部载荷及摩擦系数均对总负载力矩有显著地影响，但从结构设计的角度，仅能通过对摩擦性能的优化来实现降低负载力矩的目的。因此需采用对摆动机构的活动壳体与固定壳体接触面进行减摩处理，减小摩擦阻力，进而降低总负载力矩的方案对结构进行优化。

3 负载性能测试试验研究结构

为了验证有限元分析结果的有效性，进一步研究摆动机构的负载特性，并为这类操纵机构的总体设计提供技术和试验支持，开展了相关的试验研究。

在实际工作状态下，摆动机构不仅承受复杂的载荷环境，而且在该环境下还要实现机构的协调运动。地面试验时既要模拟使用中的外部载荷，试验装置又不能影响机构的运动，并且摆动机构的运动速度较大，这也使工程实现非常具有挑战性。

试验通过施加外部压力载荷的等效合力，即轴向载荷和横向载荷的方法来实现外部压力、过载惯性力的模拟。并采用包带加载的方式来模拟横向载荷，而轴向载荷则用橡皮绳和作动器加以实现，加载装置能够与摆裙机构同步运动。

在摆动机构的运动过程中，与运动有关的力主要包括：主动力、外部负载力、摩擦力，主动力对固定壳体球心的矩即总负载力矩。由试验测得的角位移和主动力、负载力可计算出总负载力矩和外力负载力矩，从而可得摩擦力矩。

通过对试验件进行特殊处理，使接触面上的摩擦系数约为0.1。对于采取减摩措施后的机构，对驱动力的需求显著降低，现有的操纵系统能构满足其摆动所需的驱动力要求。以俯仰方向±5°摆动的情形为例，试验测得的总负载力矩最大时刻的负载性能数据如表2 所示，结果显示不同外部载荷和摆动速度下摩擦负载占总负载力矩的比例基本保持不变，约为41%~46%，与仿真结果（40%~45%）基本一致，相同工况下试验和数值仿真得到的各负载特性的相对误差精度小于11%的量值水平。