高速飞行器姿态/参数耦合建模与鲁棒控制方案设计
李 旭,赵 洪,王辰琳,郭 栋
(1. 中国航天科技集团有限公司,北京,100047;2. 中国运载火箭技术研究院,北京,100076)
0 引 言
2010 年4 月,美国首次试飞HTV-2,再入滑翔过程中HTV-2 在空中成功进行数次机动,但在升空9 min后失控丢失。据后来分析飞行异常原因是飞行器为实现预定的高度速度只能按程序攻角飞行,导致较大侧滑引发滚转,超出可控范围。2011 年8 月美国第2次试飞HTV-2,但在飞行器升空0.5 h 后与地面失去联系,试验再次失败。事后分析认为,再入拉起滑翔阶段飞行器攻角较大,使得飞行姿态与气动参数之间的耦合程度加剧,从而引起姿态、气动参数、稳定性与操纵性之间严重耦合并最终导致滚转通道控制能力不足,触发飞行器的终止自主飞行命令。高速飞行器的飞行轨迹复杂、飞行包线范围大、大气流角飞行和倾侧转弯的侧向机动方式,使得飞行姿态与气动参数的间耦合更加明显。因此高速飞行器的再入飞行过程可以看作是一类状态与参数耦合复杂快变参数的动态系统。高速飞行器的姿态控制问题具有很强的理论意义与工程价值,许多学者在这一领域展开了研究。Georgie等将非线性动态逆方法运用于再入姿态控制问题中。但动态逆方法依赖于精确的建模,较大的外扰与参数不确定性会使得控制效果变差。文献[4]运用模糊神经网络观测系统受到的外扰与不确定项,并构造控制信号对系统进行补偿。为提升再入过程中控制系统的鲁棒性,削弱通道间耦合作用的不利影响,一些学者运用自适应滑模理论、定量反馈理论与自适应动态规划理论设计了再入姿控方法。有的学者进一步对再入过程中的黑障因素进行了建模,并提出相应的鲁棒抗扰控制方案。上述方法在建模过程中,直接将系统受到的干扰与不确定性以附加干扰项的形式体现在动力学系统中。若系统存在状态与参数之间的耦合,观测器仅能观测到同时包含有系统扰动与耦合项的复合扰动信息,无法实现扰动与耦合之间的分离。
针对上述问题,建立了状态/气动参数扩维耦合姿态动力学模型,分析了姿态/参数间的耦合特性。给出了基于观测器的扩维系统鲁棒控制方案,完成了三通道上快慢控制回路设计。通过数值仿真,验证了扩维耦合建模的正确性与鲁棒控制方案的有效性。
1 高速飞行器姿态/参数耦合建模
1.1 高速飞行器姿态动力学模型
适用于控制系统设计的绕质心姿态动力学外环仿射非线性动力学方程:
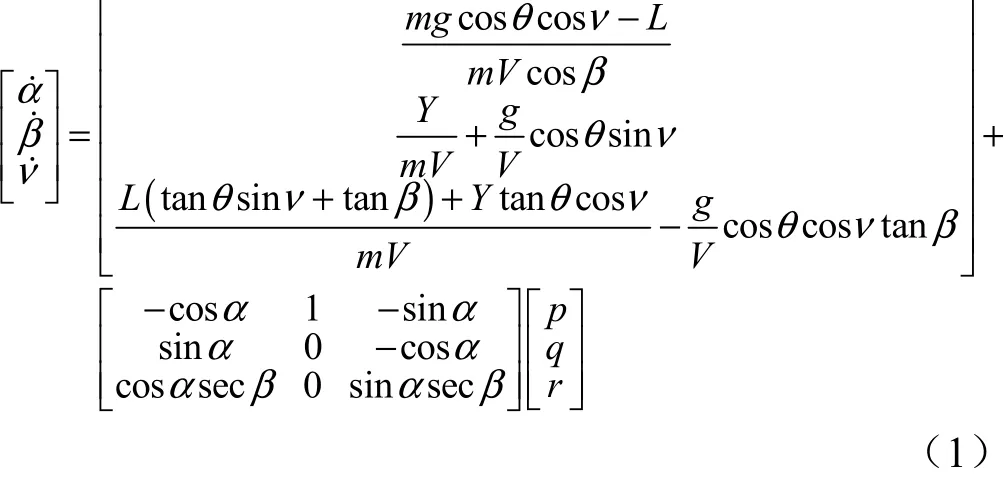
式中,,分别为攻角、侧滑角和倾侧角;,,,分别为飞行器的质量、所受引力加速度、速度和弹道倾角;,,分别为飞行器绕弹体轴,轴和轴的绝对角速度分量;,分别为飞行器受到的升力和侧向力。
内环仿射非线性姿态角速度运动学方程:
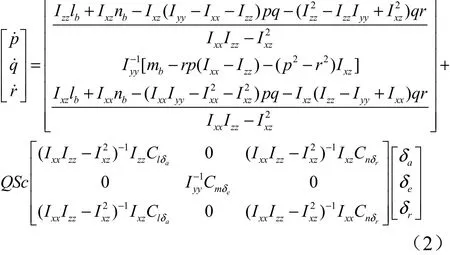
式中,,分别为弹体的滚转力矩、俯仰力矩和偏航力矩;,,分别为飞行器的动压、参考面积与参考长度; ,δ ,分别为飞行器滚转通道、俯仰通道与偏航通道上的舵偏角;C ,C ,分别为飞行器滚转通道、俯仰通道与偏航通道上的控制力矩系数偏导数。
1.2 状态/参数扩维耦合建模与特性分析
高速飞行器姿态与参数之间的耦合,最直接的表现就是气动参数的变化超出预期:飞行参数会随着飞行状态的变化而变化,而飞行器的动力学行为又反映着参数的变化,参数的变化又会使得状态发生改变,进而使得飞行参数发生变化,并可能超出预期值。因此需要将上述耦合机理反映在飞行器的姿态动力学方程中。文献[4]借鉴非线性系统中的抗扰动处理思想,提出了附加耦合项建模方法,将状态/参数耦合效应以附加项的形式反映在系统的动力学方程中。因此本文借鉴扩张状态观测器理论,将状态/参数耦合项扩张为原动力学系统的一个新状态。导出增广方程后与原动力学方程组联立,即可得到扩维后的动力学系统:
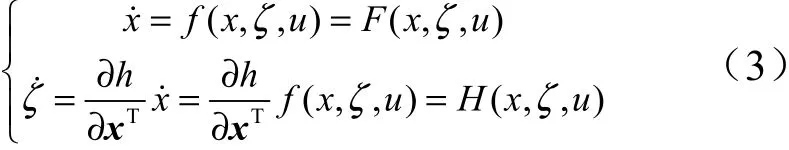
式中,,分别表示系统的状态变量,参数和控制变量;式(3)中的第2 式表示系统参数与系统状态之间的函数关系。对上式进行泰勒展开后得到:
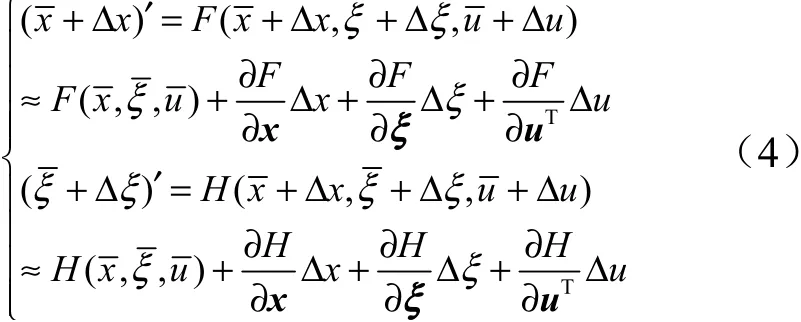
对式(4)进一步整理,可以得到系统摄动情形下状态与参数间的关系式:
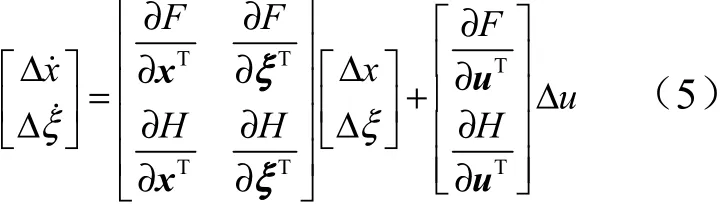
式中 Δ,Δ 分别为由耦合引起的状态摄动量和参数摄动量。式(5)状态矩阵中的非对角元即表示状态/参数之间的耦合,可运用非对角元的模值来定量分析系统的耦合程度。系统中的参数不确定项与扰动项是以附加项的形式体现在扩维后的系统中,亦实现了状态/参数耦合与系统扰动的分离。采用上述状态/参数扩维耦合建模方法,结合高速飞行器姿态动力学模型,即可建立纵向通道与横侧向通道上的姿态/参数扩维耦合动力学模型。
以俯仰通道为例,对于角度回路,主要关注攻角与升力系数之间的耦合。基于式(4),可得攻角与升力系数间的耦合形式:
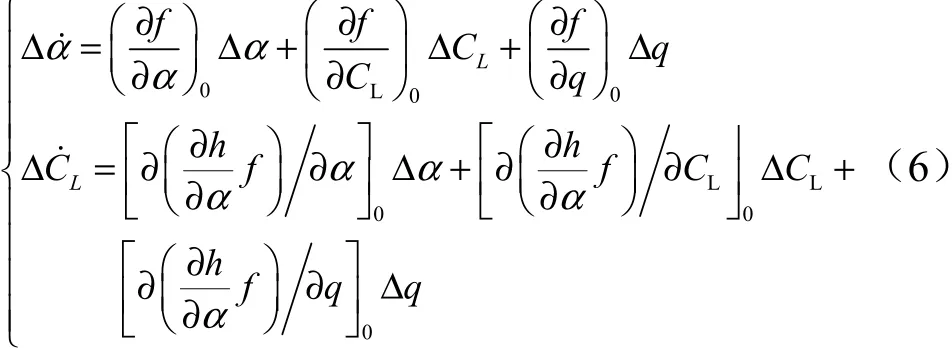
式中 带有下标0 的项表示标称轨迹处的参考值。
将式(1)中纵向通道角度回路中的物理量带入到式(6),忽略高阶项与小量后可得:
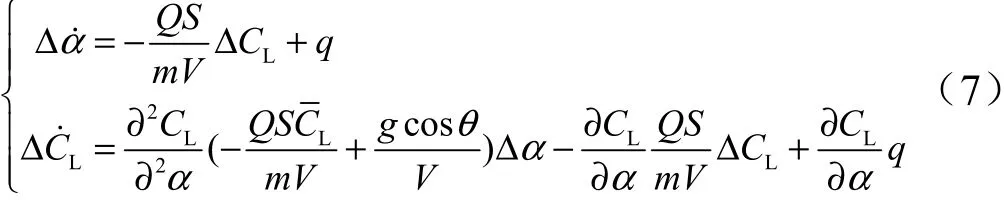
对于纵向通道角速度回路,主要关注俯仰角速度与俯仰力矩系数之间的耦合。类似于纵向通道角度回路的处理,可得如下的姿态/参数耦合形式:
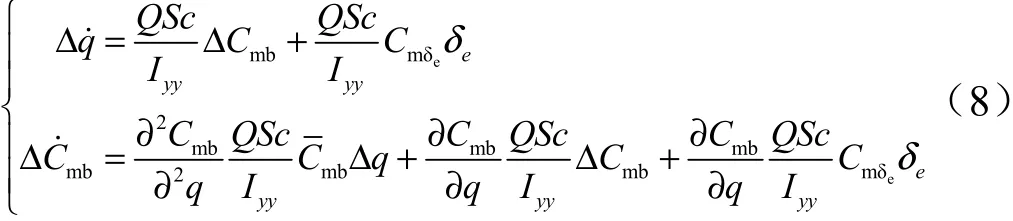
1.3 飞行姿态/参数耦合特性分析
基于某高速飞行器的典型飞行数据,采用上述方法,以俯仰通道为例分析角度回路中的姿态与气动系数之间的耦合关系。在该段标称弹道数据中,指令攻角呈逐渐减小趋势,指令侧滑角呈逐渐增大趋势。图1分别给出了纵向角度回路中攻角与升力系数之间的相互耦合作用。由图1 可以看出,随着攻角的逐渐减小,二者之间的相互耦合程度也呈现出减少的趋势。同时,气流角越大,耦合矩阵中的非对角元项的权重越大,即姿态与气动参数之间的耦合越严重,这些因素都要在姿控系统设计过程中予以考虑。
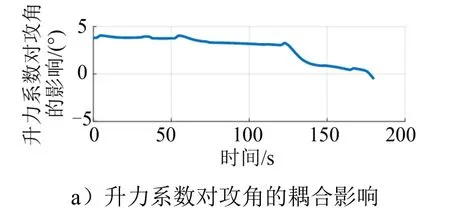
图1 纵向通道角度回路姿态/参数的相互耦合影响Fig.1 Coupling Effect of Attitude/Parameter of Longitudinal Channel Outer Loop
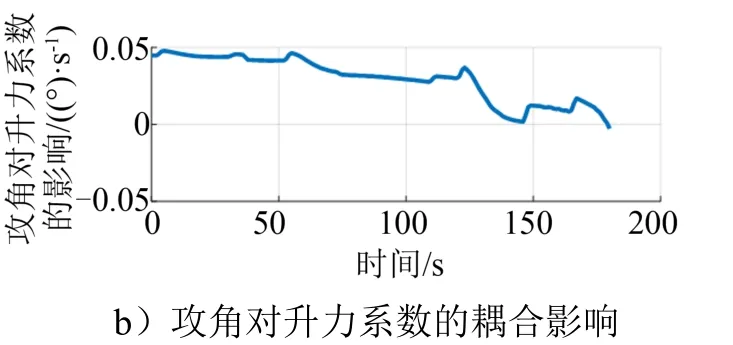
续图1
2 鲁棒姿态控制方案设计
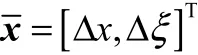

式中 Δ为由一二阶气动导数扰动项引起的系统矩阵摄动值,() 为系统受到的外扰。该增广系统状态量的维数为,参数的维数为。因系统参数是不可测的,故输出矩阵=[ ]。上述扩维系统存在较强的不确定性,传统控制方案难以满足控制效果。鲁棒控制的优点是能够在系统参数与结构存在一定范围变化的情况下,保证系统良好的控制性能。结合线性矩阵不等式,可以方便地解得满足鲁棒性能的控制参数。
2.1 基于观测器的扩维系统鲁棒控制方法
文献[10]中基于线性观测器的鲁棒控制器设计,结合式(9)所示的扩维系统给出设计过程。
首先,系统不确定项Δ需要满足如下假设:
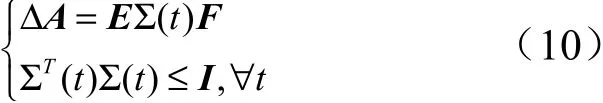
式中,为具有适当维数的已知矩阵;为未知矩阵。此外对于任意维数适当矩阵,(),,满足()()≤则对于任意> 0,有:
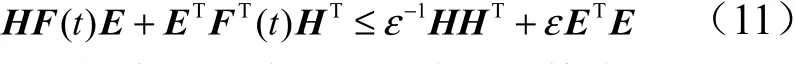
对于该扩维系统,采用的反馈控制律为

其中,=[]为反馈增益矩阵。采用的观测器为
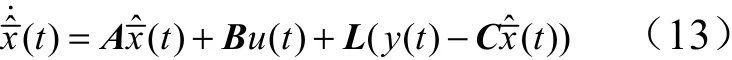
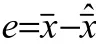
定理:针对系统(9),反馈控制律(12)与控制器(13),若存在正定对称矩阵,,对给定常数>0,若有以下两个线型矩阵不等式(LMI)成立则闭环系统渐进稳定。
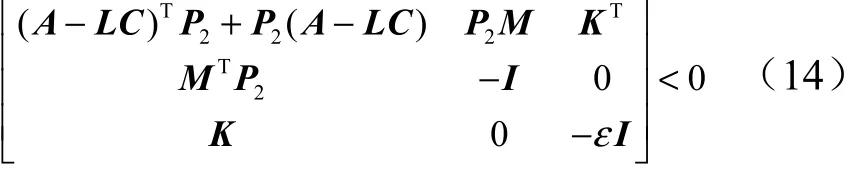

证明:取正定对称矩阵,,定义如式(16)李雅普诺夫函数:
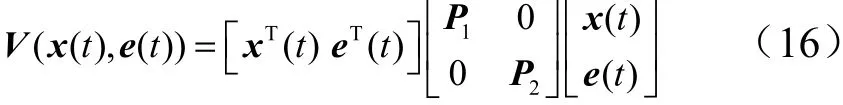
对上式求导,并根据Schur 补引理进一步可得:
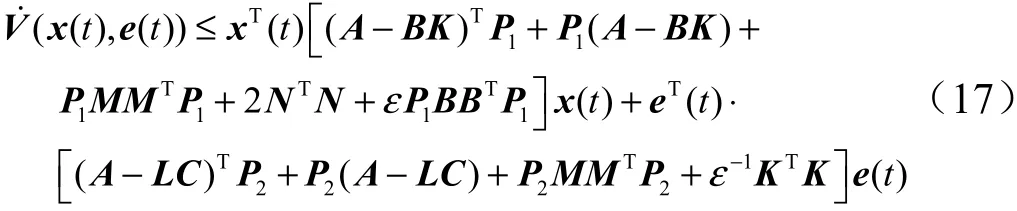
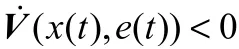
反馈控制器增益与观测器增益可由满足式(14)、(15)所示LMI 的参数,计算得到:

最终可得所设计的控制器结构图如下
图2中观测器的系统矩阵采用的是原扩维系统的标称值。可以看出,观测器基于扩维系统的输入与输出值可以同时得到状态与参数的观测值。观测量乘以反馈增益后作为控制信号作用于系统。由于控制信号中同时包含有状态与参数信息,所以该方法可以有效消减耦合带来的影响。
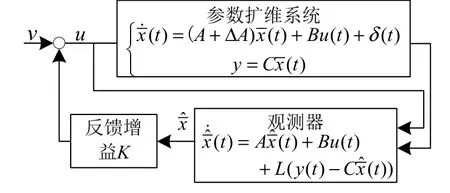
图2 基于观测器的状态/参数扩维系统鲁棒控制器结构Fig.2 Observer-based Robust Controller of State/Parameter Extended Dimension System
2.2 姿态/参数解耦姿态控制器
运用第2.1 节中基于观测器的扩维系统鲁棒控制方法,以俯仰通道为例,设计姿态/参数解耦姿态控制器。
由式(7)和式(8)可得纵向通道上角度回路与角速度回路的线性增广模型。
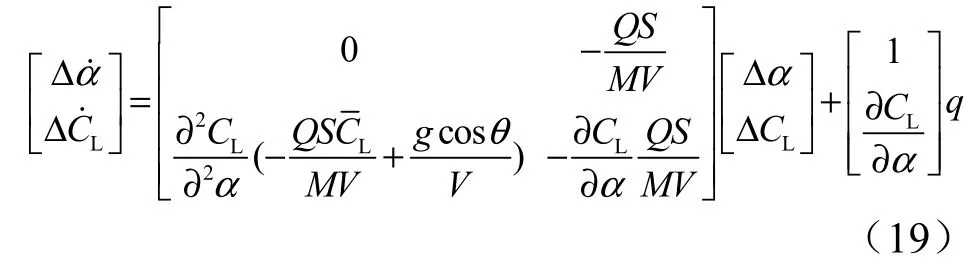
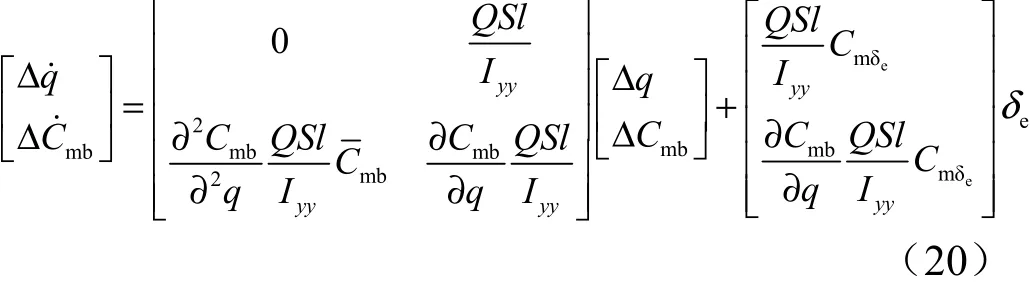
从式(19)和式(20)可以看出,气动参数的二阶导保证了扩维系统状态矩阵的非奇异,故运用该方法时需要根据标准弹道参数算得所需的导数值。图3给出了所设计的纵向控制回路。
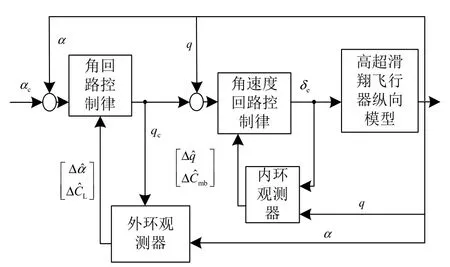
图3 纵向控制回路Fig.3 Longitudinal Control Loop
3 仿真验证
基于某高速飞行器的典型飞行任务,选取具有代表性的工作秒点如表1 所示。
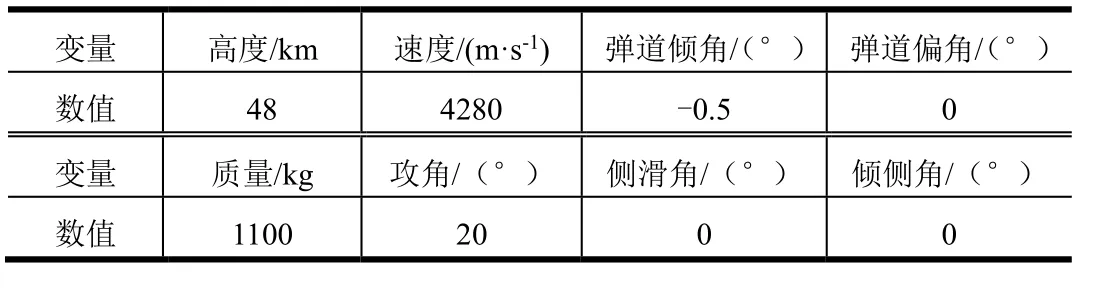
表1 工作秒点数值Tab.1 State of Working Point
在仿真初始时刻,设定指令攻角信号为20°变为15°的阶跃信号,指令倾侧角信号为0°变为40°的阶跃信号,指令侧滑角信号则始终保持0°。此外,在姿态三通道上引入了常值外扰与气动不确定项,以验证方法的鲁棒性。为进一步验证所设计方法的有效性,采用纯状态反馈控制作为对比方法。三通道上的姿态角跟踪曲线如图4 至图6 所示。图4 给出了2 种方法下的攻角跟踪曲线。可以看出,所设计观测器+耦合项补偿的鲁棒控制器在跟踪速度与跟踪精度上均优于纯状态反馈控制。图5 给出了侧滑角跟踪曲线,可以看出所设计的鲁棒控制方法在动静态特性上均优于状态反馈控制。观测器近似得到了姿态与参数之间的耦合信息。耦合信息作为控制信号的一部分,有效地削弱了耦合项的不利影响。图6 为倾侧角跟踪曲线,结果仍表明,所设计方法具有优良的跟踪性能与鲁棒性。
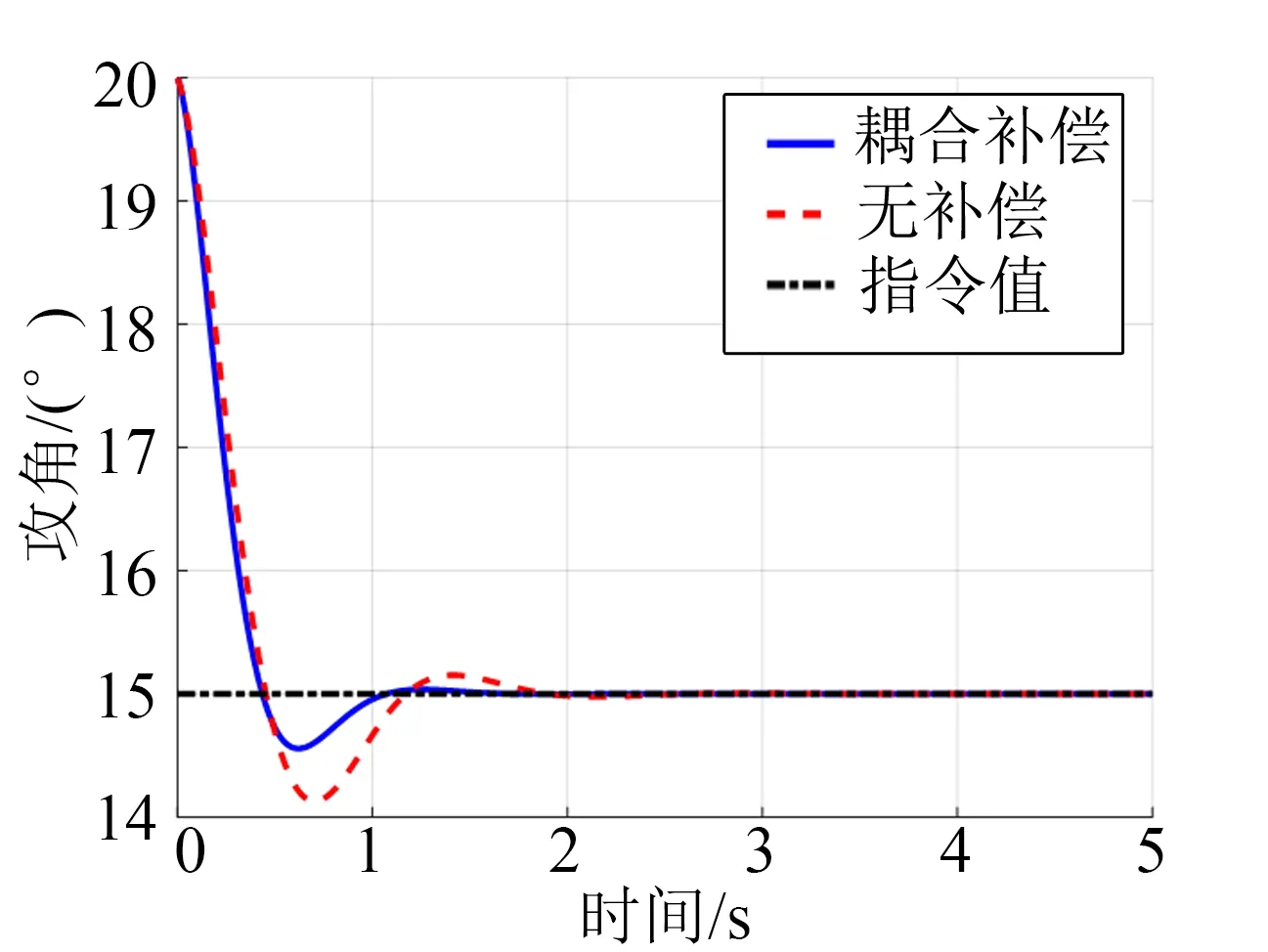
图4 攻角曲线Fig.4 Angle of Attack Curve
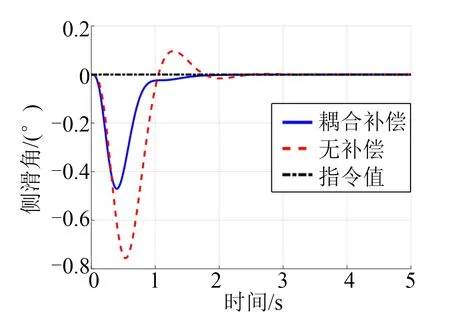
图5 侧滑角曲线Fig.5 Side Slip Angle Curve
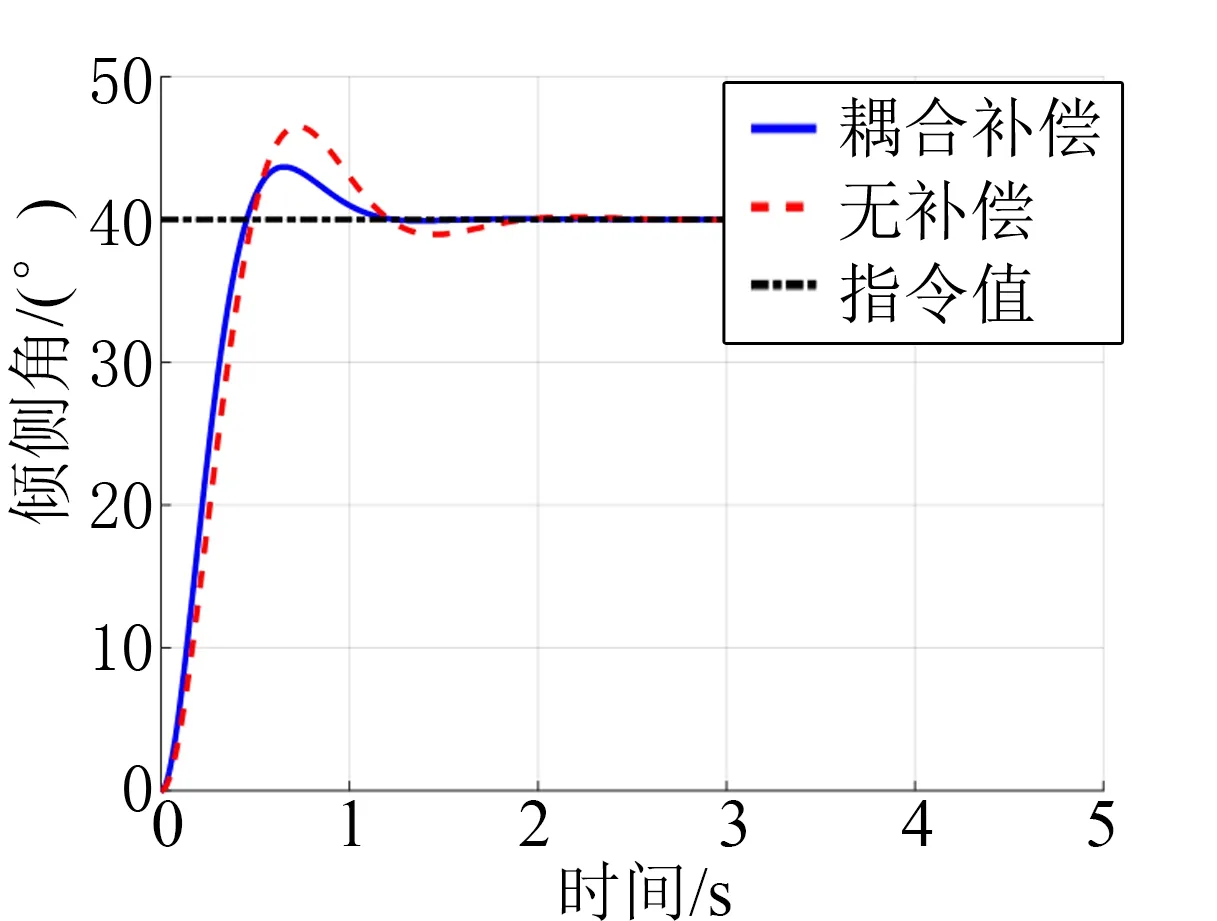
图6 倾侧角曲线Fig.6 Bank Angle Curve
4 结 论
建立了高速飞行器的姿态/气动参数扩维耦合姿态动力学模型,并完成了基于观测器的鲁棒姿态控制方案设计,理论分析与仿真结果表明:
a)采用所设计的姿态/参数扩维耦合模型,能够有效表征姿态与气动参数之间的耦合关系,实现了气动耦合项与外扰项的分离。
b)基于李雅普诺夫函数证明了控制方案的闭环稳定性。反馈控制增益与观测器增益可用LMI 计算得出。
c)基于观测器的鲁棒控制方案能够有效削弱气动耦合项对系统的不利影响,在动静态特性上均要优于纯状态反馈控制方案。

