超弹性橡胶膜片疲劳寿命及可靠性分析

尚现伟，张 强，金 平，蔡国飙

（1. 北京航空航天大学，北京，100191；2. 北京航天动力研究所，北京，100076）

0 引 言

随着近地轨道、低成本、高可靠性的可重复使用运载器（Reusable Launch Vehicle, RLV）的发展，对火箭输送系统的可重复使用性与可靠性要求越来越高。可重复使用火箭发动机是RLV 的核心动力装置， 而阀门系统作为进行发动机调节的关键部件，需要保证其在火箭多次回收利用的过程中能够可靠地工作。气动膜片球阀是液体火箭发动机中常用的一种阀门，具有可重复使用性较好、行程更大、疲劳寿命更高等优点，气动膜片球阀的工作性能和疲劳寿命主要取决于其气动执行机构中的膜片，其中应用比较多的是圆平膜片。

Atit Shah等从疲劳裂纹方面对橡胶膜片的疲劳寿命进行了研究，得到了影响橡胶疲劳性能的一部分因素。Baban Suryata等针对弹性垫层的疲劳寿命估计问题，提出了一种基于有限元分析的弹性垫层疲劳寿命估计方法，对某铁路弹性体垫层的疲劳寿命进行了预测。美国材料实验协会（American Society of Testing Materials，ASTM）就橡胶的循环疲劳试验提出了标准试验方法。

已经进行的针对圆平膜片的研究工作大多是针对减压阀、调节阀的金属膜片展开的，但对于以气动膜片球阀中的橡胶膜片研究较少。橡胶是一种超弹性材料，具有良好的伸缩性和复原性，而且材料特性和几何特性都呈非线性变化，与金属材料的线弹性完全不同。针对橡胶膜片在大行程工作过程中会涉及几何和材料两方面的非线性问题。这种情况下使用经典理论求解存在效率低、精度较差等缺陷，也不能满足高精度非线性的要求，需要对其使用非线性有限元方法进行模拟。

本文以球阀气动执行机构的超弹性橡胶膜片为对象，提出一种超弹性橡胶膜片疲劳寿命及可靠性分析方法。基于有限元方法对某气动膜片球阀的超弹性橡胶圆平膜片进行建模分析，得到橡胶膜片在阀门工作过程中的应力场，基于连续损伤理论计算橡胶膜片的疲劳寿命，以对其受力状态产生较大影响的因素，如几何尺寸、工作载荷、材料参数作为随机变量，通过试验设计，建立橡胶膜片疲劳寿命的响应面模型，使用蒙特卡洛法进行橡胶膜片疲劳寿命和可靠性的计算。

1 数学模型

1.1 有限元仿真模型

1.1.1 几何模型

本文研究的对象是球阀的气动执行机构中的超弹性橡胶膜片，图1 为某气动膜片球阀所使用的橡胶膜片及支撑结构的简化结构。橡胶膜片为完整的圆膜片，膜片的外边缘被上底座压紧，中部下端被推杆支撑，膜片和推杆之间无连接，为自然接触。上端承受气压以产生线位移，推杆底部受复位弹簧支撑。

图1 球阀气动执行机构Fig.1 Schematic Diagram of Pneumatic Actuator for Ball Valve

工作过程为：初始状态，膜片无变形，弹簧处于原位，阀门关闭。上盖充气孔充入控制气体时，推杆在橡胶膜片作用下，压缩弹簧并向下移动，阀门开启；上盖泄压过程中，膜片和推杆在膜片弹性力和弹簧弹力的作用下复位。基于Ansys 建立结构简化后的轴对称有限元模型，阀门工作过程如图2 所示。

图2 橡胶膜片的初始和工作状态Fig.2 The Initial and Terminal State of the Rubber Diaphragm

1.1.2 超弹性体材料特性

本文的研究对象膜片的材料是超弹性橡胶，高度非线性且不可压缩，涉及3 种非线性：

a）几何非线性。

当橡胶膜片在受外力时，可以呈现较大变形及翻转，当外力消失后，基本恢复原状。基于超弹性体的这种性质，将其作为球阀气动执行机构的作动膜片是可行的。在本设计中，膜片的最大变形达到37 mm。

b）材料非线性。

橡胶膜片的材料可近似为不可压缩的超弹性材料，其应力、应变表现为强非线性。主要体现在：大变形、大应变、材料的应力应变非线性严重、材料的体积近似不可压缩。目前提出的几种用来表征橡胶材料特性的函数、法则和模型，有基于统计热力学的Neo-Hookean 应变能函数、 基于热力学的Exponential-Hyperbolic 法则和基于表象学理论的Mooney-Rivlin 模 型 、 Klosenr-Segal 模 型 、Ogden-Tschoegl 模型。本文在计算过程中，选用的超弹性材料模型是一阶Ogden 模型：

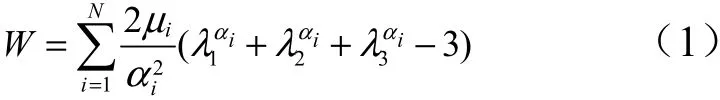
式中μ和 α为材料常数，阶数可根据实际情况进行调整。本文中采用一阶Ogden 模型进行计算。材料参数=1.21，=1.956。

c）接触非线性。

接触问题的复杂性和难点在于其接触状态的不确定性，这将给有限元计算带来严重的收敛问题，故接触问题是工程领域中复杂的非线性问题。橡胶膜片与腔体、顶杆之间的接触是高度的非线性行为，是属于刚体和柔体之间的面-面接触。接触问题也是带约束条件的泛函极值问题，较为常用的接触算法有Lagrange 乘子法、罚单元法、子结构法和基于求解器的直接约束法。本文中金属和超弹性橡胶之间的接触算法采用的是Lagrange 乘子法，在建立的几何模型中适当地施加足够的约束。

1.1.3 计算网格及边界条件

在网格划分过程中，低阶单元具有比高阶单元更好的收敛性，单元形函数的阶次越高，单元的适应能力也就越强。故本文中超弹性橡胶膜片的网格使用的单元类型为高阶单元Plane183，其具有二次位移特性，该单元可用作平面单元（平面应力、平面应变和广义平面应变）或轴对称单元。进行了不同水平的网格划分，以验证网格无关性。厚度方向划分7 层，膜片网格的单元总数为2090 个时可以满足网格无关性。图3 是结构局部网格划分情况。

图3 气动执行机构有限元模型的局部网格Fig.3 Local Mesh of Pneumatic Actuator

在计算中施加的边界条件主要为：中心轴对称约束、橡胶膜片与缸体和橡胶膜片支承片之间的成对接触面、下缸体的固定约束、推杆的回位弹簧支撑、上盖的径向位移约束、膜片周边螺栓处径向位移限制、预紧力以及工作压强。

1.1.4 有限元数值计算方法

超弹性橡胶材料相比于金属材料，其有限元分析基本方程有所不同。对于常见的金属材料，其有限元分析过程的进行基于求解单元刚度方程：

其中，为单元刚度矩阵：

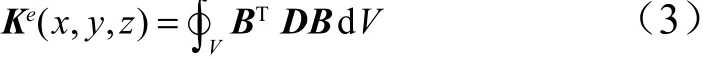
但对于超弹性橡胶材料，其本构方程中引入了应变能密度函数，是应变张量不变量、、的函数。其余求解过程与典型有限元数值计算过程相同。

1.2 疲劳寿命及可靠性模型

对超弹性橡胶膜片进行疲劳寿命计算及可靠性分析的思路是在已有非线性有限元模型基础上，以气动执行机构的几何尺寸、橡胶膜片的材料参数、工作载荷为变量，以膜片的疲劳寿命为响应值建立多项式响应面模型。利用蒙特卡洛法，在参数所分布的范围内，按照参数自身的分布规律进行抽样，将抽样结果代入到上文的响应面模型之中，可以计算得到样本点的疲劳寿命及可靠性。

1.2.1 疲劳寿命计算模型

超弹性体橡胶的疲劳寿命是基于连续介质损伤力学理论，用一阶Ogden 应变能函数导出橡胶材料疲劳损伤化方程，建立了以等效应变范围为损伤参量的疲劳寿命预测模型。

疲劳寿命可以根据其在疲劳载荷下相应的应变范围得出：

式中为橡胶常数，=1.25；为橡胶材料常数，=2163；为橡胶材料属性参数，=1.21；为橡胶材料属性参数，=1.956； εΔ 为橡胶材料在载荷下的应变范围。

1.2.2 可靠性理论与蒙特卡洛法

本文方法将疲劳寿命分析与可靠性计算相结合，首先以超弹性橡胶膜片疲劳寿命为响应量，建立二阶响应面模型。利用蒙特卡洛法，对二阶响应面方程进行取点，求解在随机因素下的疲劳寿命及可靠性分布。本文进行的响应面法采用的试验设计方法是中心复合设计（Central Composite Experimental Design，CCD）。

机械可靠度分析和设计的主要目标是求解结构的可靠度，可靠度为

式中为可靠度；f ()为研究对象包含的基本随机参数向量=(,,… ,x)的联合概率密度函数；状态函数=()用来表示研究对象的两种状态：()≤0 时为失效状态，()＞0 时为可靠状态。

基于蒙特卡洛法（Monte-Carlo）进行可靠性计算。步骤如下：

a ） 设 结 构 功 能 函 数 为=()， 其 中= (,,… ,X)为任意分布的随机参数。

b）对随机变量进行次随机抽样，得到组样本点x (= 1,2,… ,)。

c）将组样本点代入到结构功能函数表达式，得到个功能函数值Z (= 1,2,…,)。

d）设在个中存在个Z＜0（即结构失效），当充分大时，结构的失效概率为=/。

2 结果与讨论

本文提出了一种针对超弹性橡胶膜片的疲劳寿命及可靠性分析方法，通过对气动膜片球阀中的超弹性橡胶膜片及其附属结构建立有限元分析模型，分析了影响膜片疲劳寿命的主要因素，并进行试验设计，构建了二阶响应面对膜片疲劳寿命进行拟合，应用蒙特卡洛法对膜片的可靠性进行了计算。

图4为膜片应力场分布，可以看到与顶杆平直段接触的膜片区域等效应力较小，在与顶杆圆角接触的膜片下表面处出现应力集中。在膜片与下腔的圆角接触部分的膜片上表面产生了较大的应力值，此处的膜片在下腔的约束下，呈现弯曲状态，应力达到1.2798 MPa。上表面受弯程度最大，应力值最高，是危险区域，将产生危险点，危险点最先被破坏。在计算分析过程中，由于钢材和超弹性橡胶膜片强度差异较大，不考虑橡胶膜片之外结构的变形和应力。

图4 工作状态时橡胶膜片的等效应力分布云图Fig.4 Cloud Diagram of Von-mise Stress Distribution of Rubber Diaphragm in Working Condition

图5为应力在不同厚度上沿径向的分布。~分别为上表面至下表面不同厚度的径向应力分布情况。

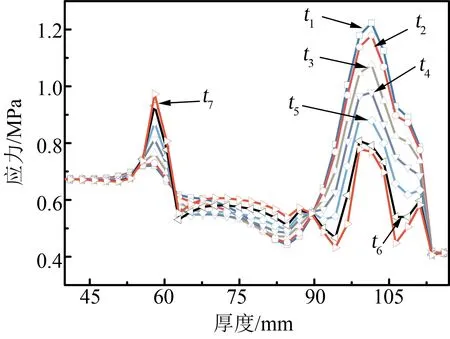
图5 橡胶膜片不同厚度中的等效应力分布Fig.5 Von-mises Stress Distribution at Different Thickness of Rubber Diaphragm

由图5 可知，在各个厚度上，膜片的应力变化趋势基本相同，第1 个峰值是推杆的圆角处，自膜片下表面至上表面，应力值逐渐减小，第2 个峰值出现在下腔圆角处，自膜片的上表面至下表面应力的峰值逐渐减小。峰值明显高于推杆处的膜片应力峰值。在膜片的其他位置，应力变化较为平缓，在膜片的各厚度处差别不大，且显著低于峰值处的应力值。膜片在工作过程中的最大等效应力的大小直接影响其疲劳寿命。

在获取膜片应力场后，基于连续损伤模型进行膜片寿命计算，并以膜片危险点寿命为响应值，建立响应面模型。表1 为进行试验设计时变量的取值范围。

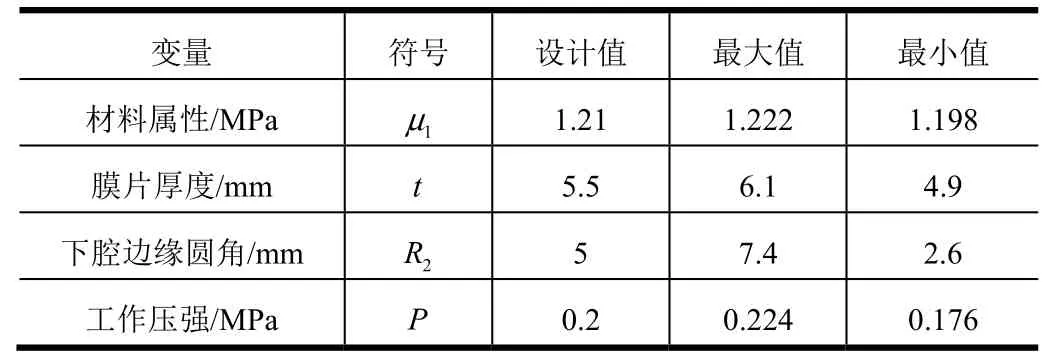
表1 试验设计中变量的取值范围Tab.1 The Value Range of Variables in the Test Design

选取对膜片的工作应力有较大影响的结构参数、材料参数、工作载荷为变量，在考虑加工限制及工作性能条件限制下，设计变量的取值范围和初始值。根据CCD 试验设计方法得到试验点的参数组合情况，共31 种试验设计组合，限于篇幅未列出。

图6为以下腔圆角值和工作载荷这两个对膜片的疲劳寿命影响较大的因素为变量，绘制的以疲劳寿命为响应的响应曲面。从图6 中可以看到，总体趋势上，随着下腔圆角的增大，超弹性橡胶膜片的疲劳寿命会增加。随着工作压强的增加，膜片疲劳寿命的响应值也会逐渐略微下降，但变化幅度较小，即橡胶膜片的疲劳寿命对工作载荷变化的敏感性比对结构尺寸的敏感性差。

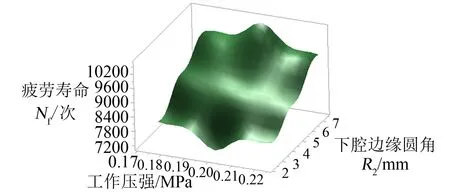
图6 疲劳寿命Nf 关于P 和R2 的响应曲面Fig.6 Fatigue Life Response Surface for Effects of P and R2

膜片的疲劳寿命对于气动执行机构的工作压强和膜片的厚度的响应曲面如图7 所示。

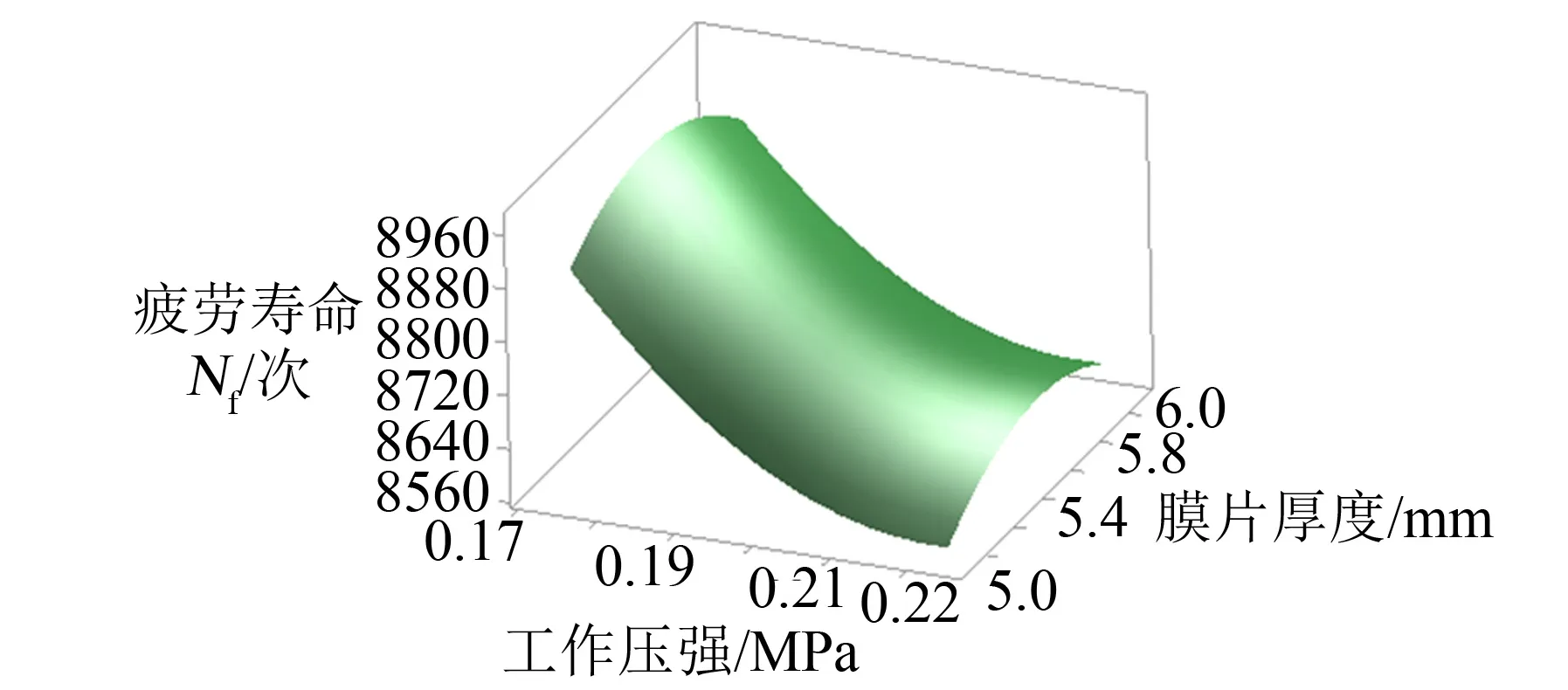
图7 疲劳寿命Nf 关于P 和t 的响应曲面Fig.7 Fatigue Life Response Surface for Effects of P and t

由图7 可知，随着工作压强的增大，橡胶膜片的疲劳寿命值降低，随着膜片厚度的增加，膜片的疲劳寿命值先增大后减小，存在峰值。说明膜片厚度对膜片疲劳寿命的影响规律与其他影响因素的规律不同，影响趋势呈现抛物线型。同时，由图7 中轴的刻度值可知，工作压强对膜片疲劳寿命的影响程度远远小于气动执行机构的下腔圆角对膜片疲劳寿命的影响程度。根据分析可知，工作气压的波动对膜片的疲劳寿命影响不大，控制膜片疲劳寿命的重点措施是控制气动执行机构的下腔圆角尺寸值。利用蒙特卡洛法，在参数分布的范围内，按照参数自身的分布规律进行抽样取点10 000 个，将抽样的结果带入已建立的二阶响应面模型中，进行统计可以得到疲劳寿命的分布情况。

图8为橡胶膜片疲劳寿命分布曲线，并使用威布尔分布对橡胶膜片的疲劳寿命进行拟合。由图8 可知，膜片的寿命在给定的参数分布下，大部分样本点的疲劳寿命值分布在8000~10 000 区间内。能够达到可重复使用的要求，而且大大高于目前常用的波纹管的寿命值。

图8 橡胶膜片的疲劳寿命分布Fig.8 Fatigue Life Distribution Curve of Rubber Diaphragm

图9为橡胶膜片的可靠性分布曲线，通过对橡胶膜片的疲劳寿命威布尔分布函数进行积分，得到了不同寿命下，膜片结构的可靠性。由图9 可知，寿命大于7800 次的可靠度为0.9 978。可靠性较高，能够满足可重复使用液体火箭发动机的要求。通过以上计算流程，可以说明本文方法能够针对超弹性橡胶膜片疲劳寿命及可靠性分布进行准确计算。

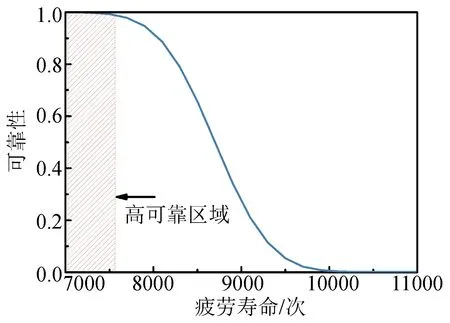
图9 橡胶膜片的可靠性分布曲线Fig.9 Reliability Distribution Curve of Rubber Diaphragm

3 结 论

为了提高液体火箭发动机阀门的可重复使用性，本文以球阀气动执行机构的超弹性橡胶膜片为对象，提出了一种超弹性橡胶膜片疲劳寿命及可靠性分析方法。在非线性有限元计算基础上，通过试验设计建立了橡胶膜片疲劳寿命的响应面模型，利用Monte-carlo法和可靠性理论进行膜片可靠性计算，得到以下结论：

a）超弹性橡胶材料能够满足大行程的设计目标，具有良好的伸缩性和复原性。使用基于应变能函数的有限元计算方法能够较准确地计算超弹性橡胶的非线性问题，效率较高。

b）气动球阀橡胶膜片在产生大变形时，内部层与层之间应力分布均匀，等效应力沿径向的变化趋势基本相同，厚度的波动对膜片内部应力的分布影响不大。在膜片曲率半径较小处产生应力的峰值明显高于膜片平直段的应力值。

c）基于连续介质损伤力学理论的橡胶膜片疲劳寿命对橡胶膜片的支承结构和工作气压的波动较为敏感，随着气动执行机构下腔圆角的减小，膜片的疲劳寿命值明显降低，随着工作气压的减小，膜片疲劳寿命略微升高。膜片的疲劳寿命对膜片的材料属性参数和膜片厚度波动的敏感性较低。

d）本文提出的方法能够针对超弹性橡胶膜片疲劳寿命及可靠性分布进行准确计算。针对所研究的算例，在设计变量的波动范围内，阀门超弹性橡胶膜片疲劳寿命值大于7800 次的可靠度为0.9 978。控制加工尺寸和工作载荷的波动能够提高膜片的疲劳寿命，使得橡胶膜片具有较高的可重复使用性，以及更高的可靠性，能够满足可重复使用液体火箭发动机的要求。