地铁隧道普通环管片缓和曲线理论排版简化计算与应用技术
连逢逾,王国义
(1.成都轨道建设管理有限公司,四川 成都 610093;2.中电建成都建设投资有限公司,四川 成都 610212)
近年来盾构隧道的管片理论排版和选型不当,直接造成管片错台与破损,影响管片拼装质量。关于管片理论排版和选型问题国内有许多学者进行了相关研究,并形成了相关的研究成果。
管天有等[1]通过建立数学公式精确计算缓合曲线上的管片超前量,确定了隧道内缓合曲线上所需转弯环的管片数量。侯刚[2]通过缓合曲线长度、切线角和圆曲线半径等参数探索出在缓合曲线上准确选择弯环管片理论排版的方法。韩艾芳[3]结合某小半径隧道转弯施工实际情况,对盾构隧道小转弯半径下的管片选型进行探索、总结。田春雨等[4]详细分析了成都地铁普通环管片特点,提出管片圆曲线理论排版的简化计算公式。程明等[5]提出了使用推进油缸和铰接油缸行程差来计算管片的楔形量,从而确定转弯环管片的拼装点位。孙锦涛[6]提出了管片适应盾尾间隙、结合盾构机姿态、与盾构机操作司机协调的管片选型原则和方法。孟宪凤[7]提出根据推进油缸差选用管片,在2个相反方向上的行程差不小于50 mm时就应该拼装转弯环。已有研究中主要是现场施工专家根据实际管片选型经验从多因素分析管片选型注意事项,对缓合曲线的理论排版研究较少。
本文基于成都轨道交通19号线二期工程等腰梯形普通环管片特点,推导分析出了基于缓合曲线总长、圆曲线半径和等差数列求和等方法下,7个分块组成的单环管片缓和曲线理论排版的简化计算公式,并实现了借助Excel简化计算公式的缓和曲线安装转弯环位置的快速计算方法。
1 成都轨道交通19号线二期工程管片特点
成都轨道交通19号线二期工程采用普通环管片对设计隧道平纵曲线拟合,普通环管片分为直线环、左转弯环、右转弯环3种管片,管片技术参数如表1所示,每环管片由7块管片组成,即4块标准块(B),2块邻接块(L),1块封顶块(K),由盾构上的拼装机拼装成一个整环,右转弯环管片组成如图1所示。
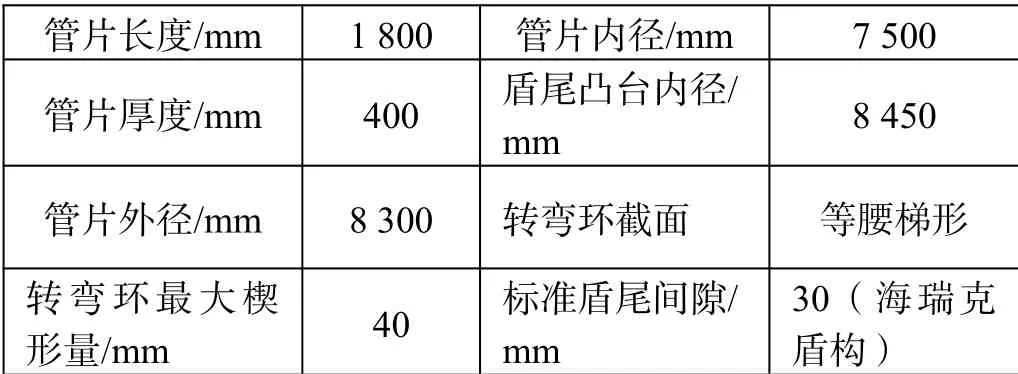
表1 管片技术参数表
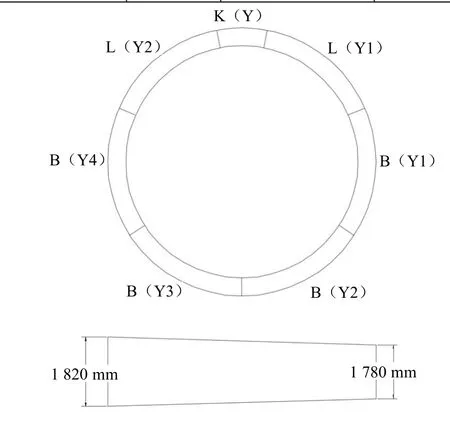
图1 右转弯环管片示意图
成都轨道交通19号线二期工程管片采用错缝拼装,管片拼装点位是以封顶块的中线位置来定义的,有19个点位,相邻点位之间角度约19°,封顶块拼装在18点位,如图2所示。转弯环不同的拼装点位在水平面和竖直面中有不同的楔形量,达到不同的平纵曲线转弯半径。为了能够顺利拼装管片,封顶块一般安装在上半部分,上半部分的点位有1、2、3、4、15、16、17、18、19这9个点位。为防止管片下掉,一般不拼装19点位。
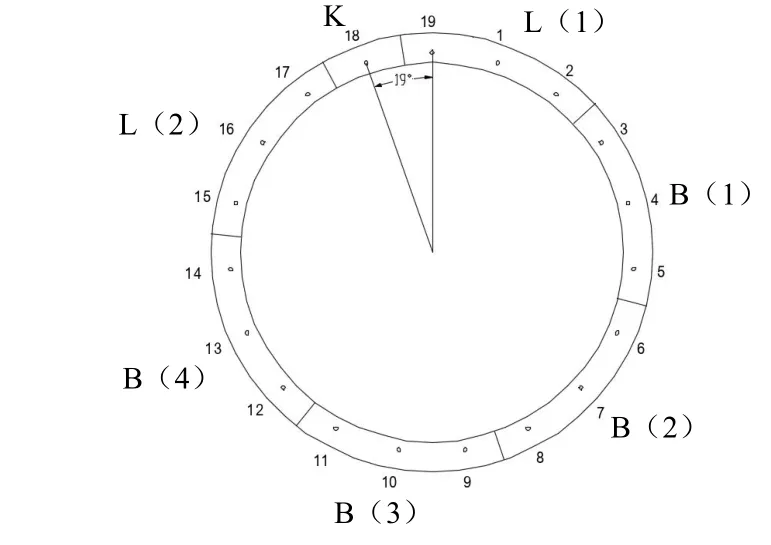
图2 管片拼装点位图
转弯环在不同点位条件下曲线楔形量的计算这里不再推导、计算,只是将右转弯环在上半部分不同点位条件下的楔形量汇总表进行统计,如表2所示。

表2 右转弯环楔形量计算表(单位:mm)
根据汇总表可知采用错缝拼装方式转弯环水平转弯的楔形量最大是40 mm。转弯环不同的拼装点位有不同的楔形量,不同的楔形量转弯环和直线环的组合拼装可以拼装出不同半径的曲线。为防止封顶块下落,一般不建议拼装19点,在盾构管片拼装中尽量使用最大楔形量的拼装点位(1点或18点),不需要转弯环时使用直线环拼装,这样使用转弯环数量最少,同时理论排版和实际排版才更加接近。因此,管片选型中水平转弯的楔形量要按照37.83 mm计算。左转弯环的情况与右转弯相反,这里就不再列举。
2 缓和曲线的理论排版简化计算
2.1 曲线简述
隧道线路根据直线和缓和曲线的连接位置不同,分别为直缓点、缓圆点、圆缓点、缓直点4种类型,按照位置不同分别用ZH、HY、YH、HZ标识,如图3所示。

图3 隧道曲线段示意图
2.2 圆曲线理论排版的简化计算
设管片内径为Φ内,外径为Φ外;设水平转弯半径为R,管片拼装最大楔形量为&,管片宽度为L,计算圆曲线理论排版简化公式如下。
求转弯半径为R条件下掘进1 m理论所需楔形量&1,如图4所示。
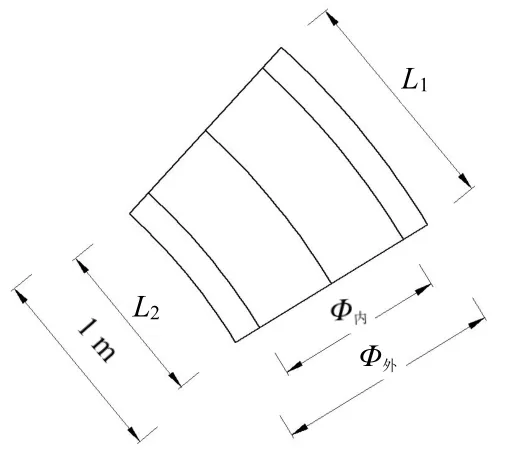
图4 圆曲线楔形量计算图
根据相似三角形可知:
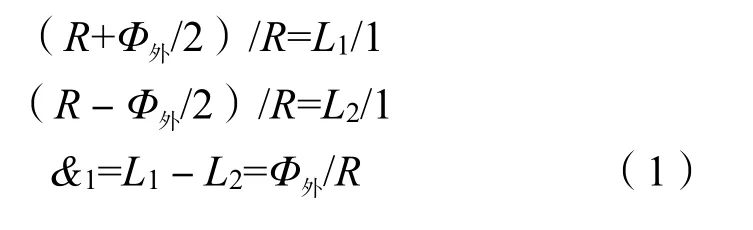
设半径为R的圆曲线长度为L总,所需转弯环X环,所需直线环Y环,求理论排版简化计算,即(LX+LY)&1=X&,可求出X=LY&1/(&-L&1)。
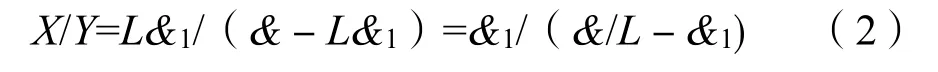
普通环管片圆曲线理论排版计算举例,设R=600m,Φ外=8 300 mm,L=1.8 m,&=37.83 mm,求得&1=8 300/600=13.83(mm/m),X/Y=13.83/(37.83/1.8-13.83)=1.9∶1。
对于不同转弯半径下的圆曲线通过式(1)、式(2)都可以准确计算出理论排版。
2.3 缓合曲线理论排版的简化计算
缓和曲线由于从ZH到HY或从YH到HZ曲线半径是均匀、逐渐变化的,从而每米所需的楔形量是从0到&1(ZH到HY)或从&1到0(YH到HZ)均匀变化的过程,进而可判定缓合曲线每米楔形量的变化量是等值的。当楔形量达到拼装转弯环的楔形量时,就要拼装转弯环。
设圆曲线半径为R,从ZH到HY或从YH到HZ距离为L缓,起始点(ZH或YH)每米楔形量为&起,结束点(HY或HZ)每米楔形量为&终,缓合曲线每米楔形量的变化量为&缓,拼装的转弯环为第i环,离起始点距离为Li。按照选型经验当楔形量为0.5&、1.5&、2.5&、……、(i-0.5)&时都要拼装一环转弯环,拼装点位为1点或18点。拼装转弯环所需的楔形量实际上是以缓合曲线每米楔形量的变化量&缓为等差值的数列的和。
由各个参数可知:
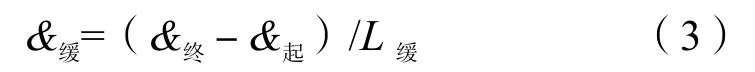
当缓和曲线从ZH到HY时:

当缓和曲线从YH到HZ时:

将等差数列求和公式代入拼装转弯环的楔形量计算公式中:

由式(6)可求出Li:

式(7)就是缓合曲线拼装转弯环位置的简化计算公式,当然在实际中Li是无负值或不能大于L缓值的,Li值实际计算出来要加以判断确定。
当缓合曲线起点是ZH,结束点是HY时,由式(7)和式(4)可知:
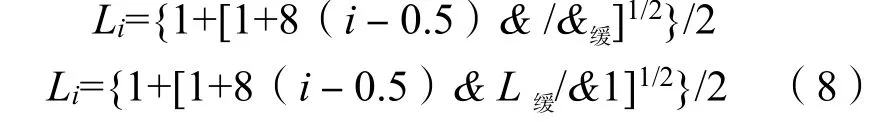
当缓合曲线起点是YH,结束点是HZ时,由式(7)和式(5)可知:
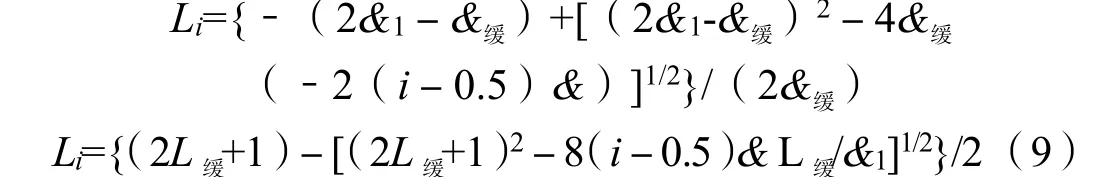
式(8)计算出来的Li值就是从ZH点到HY点拼装转弯环第i环的位置;式(9)计算出来的Li值就是从YH点到HZ点拼装转弯环第i环的位置。
3 缓合曲线理论排版的实例计算
现通过实例采用Excel表格计算缓合曲线的理论排版。
设采用19号线二期工程的等腰梯形转弯环管片,理论排版拼装点位为1点或18点,楔形量&为37.83 mm,圆曲线半径为800 m,从ZH点到HY点和从YH点到HZ点总长L缓都为80 m,求缓合曲线的理论排版。
由式(1)可知:&1=Φ外/R=8 300/800=10.375(mm/m)
3.1 从ZH点到HY点的缓合曲线理论排版
采用Excel表格将圆曲线半径、缓合曲线总长代入式(8)中就可以计算出缓合曲线理论安装转弯环的位置,如图5所示。
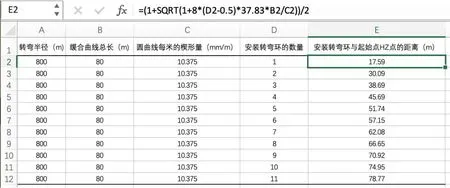
图5 从ZH点到HY点的缓合曲线理论排版Excel计算图
3.2 从YH点到HZ点的缓合曲线理论排版
采用Excel表格将圆曲线半径、缓合曲线总长代入式(9)中就可以计算出缓合曲线理论安装转弯环的位置,如图6所示。
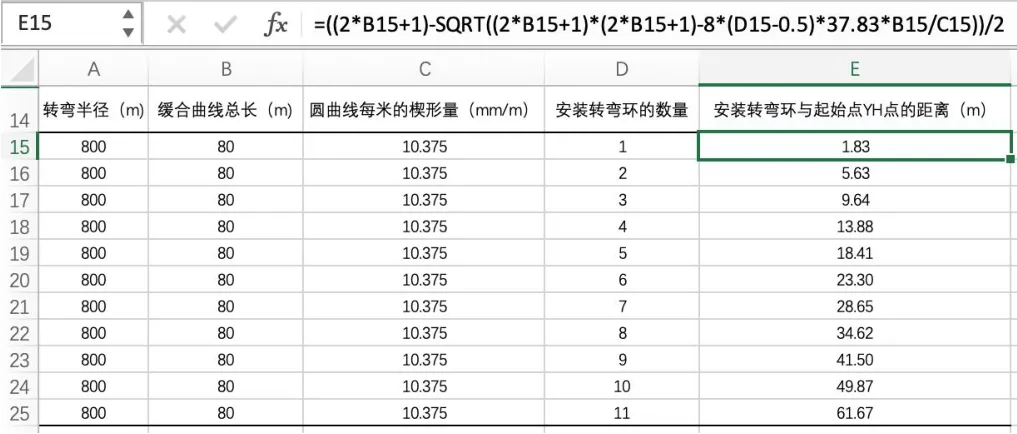
图6 从YH点到HZ点的缓合曲线理论排版Excel计算图
综上所述,借助Excel简化计算公式的缓和曲线安装转弯环位置的快速计算。当然在实际选型过程中,要综合考虑转弯环的理论安装位置、盾尾间隙、油缸行程差和盾构纠偏等多种因素,确保盾尾间隙在正常范围内。
4 结论
借助理论排版计算公式,可实现不同半径盾构管片的圆曲线简化理论排版。推导分析出了基于缓合曲线总长、圆曲线半径和等差数列求和等方法下,7个分块组成的单环管片缓和曲线理论排版的简化计算公式,该计算公司具有快捷、方便、便于应用等特点。借助Excel简化计算公式,可实现缓和曲线安装转弯环位置的快速计算,对盾构管片理论排版具有一定的借鉴和参考作用。

