基于颗粒动理学理论的双梯度钻井数值模拟

刘 浩，杨璎珞，王湘萍，王淑彦，邵宝力，李田田

(1.东北石油大学 石油工程学院提高油气采收率教育部重点实验室，黑龙江 大庆 163000； 2.黑龙江八一农垦大学 工程学院，黑龙江 大庆 163000； 3.大庆油田有限责任公司 第二采油厂，黑龙江 大庆 163000)

深水钻井技术面临着许多挑战[1-3]，例如,安全压力窗口狭窄和套管程序较为复杂等问题。随着深海钻井技术的发展，单一的混合液压力梯度已无法提供安全的压力窗口。双梯度钻井(DGD)技术可以有效地增加孔隙压力和地层破裂压力之间的安全窗口[4]。该技术可以降低井筒中混合流体的密度，并在环空井筒中产生两种压力梯度，进而减少套管数量，避免井喷事故的发生。空心球DGD技术是深海钻探中应用较为广泛的方法之一，该方法具有成本低、污染小等优点[5]。DGD钻井液循环系统内存在两种组分的固相颗粒—岩屑和空心球，因此可以通过改变井筒内混合液的密度来控制环空中的压力分布，进而实现安全可靠的钻井过程。

计算流体动力学(CFD)是预测钻井过程中流体流动行为和岩屑运移规律的有力工具，该方法已经显示出其在复杂钻井工况模拟及预测方面的优势[6-7]。Heydari等[8]通过CFD方法研究了不同偏心度的条件下环空井筒中岩屑的积聚情况，结果表明，岩屑的积累量会随着偏心度的增大而增大，同时岩屑的积累程度也受到钻杆转速的影响。此外，Ghasemikafrudi E等[9]通过数值模拟分析了钻杆偏心距对岩屑流速和钻井液流速的影响。Makuach J M[10]研究了一系列变量(如泥浆质量、岩屑尺寸和循环速率)对斜井岩屑输送效率的影响。Pang Boxue等[11]基于双流体模型，结合颗粒动理学理论，模拟了非牛顿流体以及岩屑的运移规律。同时，CFD方法也已经成功应用于对脉冲射流钻井这项新技术的模拟计算，并在分析射流对岩屑的输运能力方面取得了一定的成果[12]。

CFD方法[13-14]已广泛应用于常规钻井过程的研究，可以预见其在双梯度钻井中具有广阔的应用前景，能够处理复杂流体的多相流动问题，特别是针对受实验仪器所限而难以测量的各类流动问题。Zhang Ruiyao等[15]采用标准k-ε湍流模型对空心球分离器内部的流场进行了描述，同时模拟了钻井液在分离器内的流动行为。考虑到双梯度钻井过程中钻井液所受到的提升力，Wang Xuerui等[16]对动量方程进行了修正并建立了井筒内压力的分布模型。目前关于空心球和岩屑具体流动行为的数值模拟研究较为有限，本文采用基于颗粒动理学理论的Eulerian-Eulerian双流体模型来模拟岩屑和空心球的流动行为，同时分析了空心球密度与钻杆转速对岩屑运移情况的影响，研究了环空井筒内部的流体力学特性，并为DGD工艺提供了理论指导。

1 液固两相流数学模型

以Eulerian-Eulerian双流体模型作为基础，模拟了注入管线和环空井筒中的液固两相流动行为，同时结合颗粒动理学理论对颗粒间的相互作用进行了研究。为了简化模拟过程，假设：①岩屑和空心球的尺寸以及密度是均匀的；②液固两相之间不存在界面传质。

1.1 守恒方程

环空井筒以及注入管线中的空心球与岩屑均被视为拟流体，二者与钻井液的流动均遵循Navier-Stokes方程，各相的连续性方程可表示为：

(1)

式中，εi为第i相的体积分数；vi为第i相的速度矢量；ρi为第i相的密度。

环空井筒内与注入管线内的钻井液的动量守恒方程如下：

(2)

式中，g为重力加速度；pl为液相静压力；τl为液相应力张量。

空心球和岩屑的动量守恒方程如下：

(3)

式中，下角标s为颗粒相；β为钻井液与颗粒之间的阻力系数；τs为颗粒相的应力张量；ps为颗粒相压力。

1.2 液相湍流模型

本文采用SST-k-ω模型[17]进行求解计算，该模型是基于k-ε模型与k-ω模型所发展形成的优化模型。在该模型中，湍动能与耗散率[18]的求解如下：

(4)

(5)

式中，k为流体湍动能；ω为流体耗散率；Γk为湍动能的扩散率；Γω为耗散率的扩散率；Gk为速度梯度所产生的湍动能；Gω为速度梯度所产生的耗散率；Yk为湍流引起的湍动能；Yω为湍流引起的耗散率。

(6)

式中，σk为湍动能的普朗特数；σω为耗散率的普朗特数；μt为湍流黏度。

1.3 颗粒动理学方程

颗粒动理学(KTGF)是近年来发展起来的一种描述高浓度颗粒流动特性的研究方法，该方法利用气体分子动力学的基本理论来表述颗粒之间的流动情况，并通过研究颗粒间的碰撞来进一步描述动量传递与能量交换[19-21]。颗粒相的压力与颗粒温度间的方程关系如下：

(-psI+τs：·vs+·(ks·θs)-γsφls

(7)

式中，(-psI+τs)：·vs为应力张量所产生的能量项；ks·θs为能量扩散项；ks为扩散系数；γs为能量耗散相；φls为能量交换相。

颗粒相应力张量：

τs=

(8)

式中，I为单位矢量；ξs为颗粒相黏度；μs为颗粒相剪切黏度。

颗粒黏度及其剪切黏度分别用公式表示为：

(9)

(10)

式中，ds为颗粒直径；g0为径向分布函数；e为恢复系数；θs为颗粒温度。

2 深水井筒数值模拟设置

2.1 几何建模

模拟过程中采用了压力基求解器，该方法源自于早期的Segregated求解器，并在此基础之上增加了耦合算法。计算域模型包括环空井筒以及空心球注入管线，实际工况中的井筒长度较长，为了简化模拟过程，本研究所选取的环空井筒段长度为50 m，空心球注入管线长3 m，套管外径0.4 m，钻杆直径0.128 m，均依据美国石油学会标准进行选取。将钻孔底部的岩屑进口设置为坐标原点基准面，注入管线位于环空井筒中部，高25 m，注入管线入口直径0.2 m，混合流体的出口位于环空井筒的顶部，具体几何结构如图1所示。

图1 计算模型几何结构示意Fig.1 Geometric structure of calculation model

2.2 数值模拟参数

本文的数值模拟过程采用商业软件Fluent18.0进行处理计算，模型总网格数为2.8×105，并通过设置滑动网格实现井筒和钻杆之间的相对旋转。瞬态计算的平均时间步长值为0.001 s，实际流动过程持续30 s。在25 s后的流动状态趋于稳定，因此对25～30 s的模拟结果进行平均取值。空心球与岩屑的注入速率均为0.024 m3/s，初始速度均为2 m/s，其中岩屑直径2 mm，空心球直径5 mm。模拟过程中的空心球密度分别为320、460、600 kg/m3，钻杆转速分别为100、200、300 r/min。

3 计算结果与分析

3.1 空心球密度对岩屑运移情况的影响

研究选取了空心球规格表中3种不同密度规格的空心球进行数值模拟计算。环空井筒中距离井底25 m处以及截面上方部分井筒中空心球和岩屑的浓度分布如图2所示。当空心球密度改变时，在注入管线以下的岩屑颗粒的流动状态基本不受影响，而从注入管线与环空井筒的交界处开始，浓度云图呈现出颜色的过渡状态，这表明空心球与岩屑颗粒在该位置开始进行混合。在注入管线中，密度为320 kg/m3的空心球的高浓度区域主要存在于管线上方，这是由于低密度空心球更容易被钻井液携带，并且在浮力的作用下聚集在注入管线的上方区域。随着空心球密度的增加，25 m截面处岩屑浓度的云图颜色逐渐变浅，这是由于高密度空心球具有更大的惯性，进而对注入管线截面处的岩屑浓度具有更大的削减作用。当空心球注入到竖直井筒当中以后，3组浓度云图中低密度空心球所对应的颜色深度下降地更快，这表明低密度空心球可以更加迅速的与岩屑进行混合。

图2 不同空心球密度条件下注入管线处颗粒浓度分布Fig.2 Particle concentration distribution at injection pipeline under different density of hollow spheres

竖直管段中28～36 m处岩屑的浓度与流速分布如图3所示。图3(a)中，3段云图在28 m截面处均出现了岩屑的低浓度蓝色区域，而在36 m截面处低浓度蓝色区域均已消失。这表明两种颗粒沿着环空井筒上升方向在钻井液与钻杆的共同作用下产生了较为均匀的混合，同时空心球密度的变化会影响到颗粒间的混合程度。当空心球密度增大时，井筒中岩屑的高浓度区域随之增加，这表明减小空心球密度可以改善岩屑与空心球的混合程度，从而避免岩屑聚集。如图中右侧所示，当所注入的空心球密度为320 kg/m3时，岩屑流速云图中28～32 m处的颜色较深，这表明当岩屑与空心球密度相差较大时，二者在混合初始阶段更容易产生高流速区域。随着井筒高度的增加，岩屑流速逐渐趋于稳定。

图3 不同空心球密度下竖直管段内岩屑浓度与流速分布Fig.3 Concentration and velocity distribution of cuttings in vertical pipe section under different density of hollow spheres

环空井筒中混合流体静压力的变化情况如图4所示。注入点前后存在两种不同的压力梯度，在井筒中0～25 m内混合流体的压降要大于25～50 m内的压降，这表明空心球的注入可以有效地实现双梯度钻井的工作思路。当空心球密度减小时，蓝、红、黑三种颜色所代表的压力曲线依次下降，曲线之间的压力差值为3～6 kPa。该趋势表明减小空心球密度可以进一步降低混合流体的静压力，从而更好地实现双压力梯度的目的。

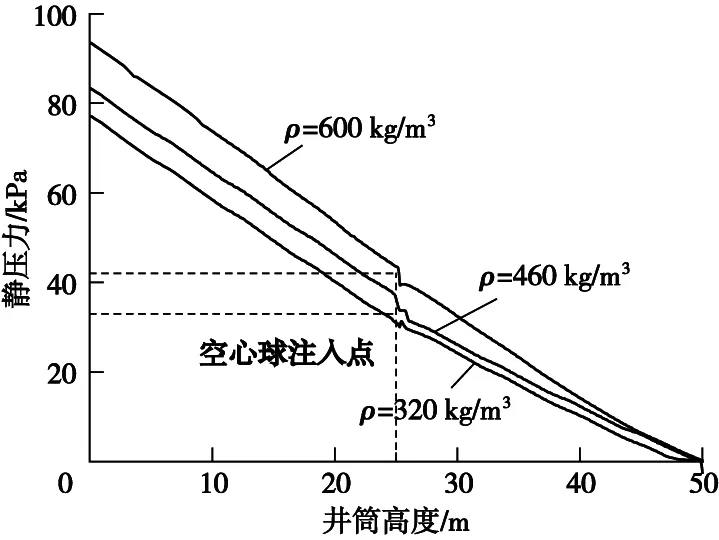
图4 不同空心球密度下混合流体静压力分布Fig.4 Static pressure distribution of mixed fluid under different density of hollow spheres

3.2 钻杆转速对岩屑运移情况的影响

钻杆转速对竖直管段中岩屑浓度与流速分布的影响如图5所示。当钻杆转速为100 r/min时，岩屑浓度云图中高浓度与低浓度区域的分布较为明显，当转速增加到300 r/min时，岩屑浓度云图中的红色与蓝色区域范围明显减小。该趋势表明增大钻杆转速可以避免产生岩屑浓度过高或过低的区域，使岩屑的浓度分布更加均匀，减少聚集现象。如右侧的岩屑流速云图所示，随着钻杆转速的升高，红色的高流速区域的范围逐渐减小，这表明提高转速可以促使岩屑在井筒中的速度分布更加均匀，进而提高两种颗粒的混合效果。

图5 不同转速条件下竖直管段内岩屑浓度与流速分布Fig.5 Concentration and velocity distribution of cuttings in vertical pipe section at different rotating speeds

不同转速条件下颗粒拟温度随浓度变化情况如图6所示。由图6可以看出，钻杆转速的改变对颗粒拟温度的分布产生了一定影响。颗粒拟温度表征的是颗粒脉动强度的大小，而颗粒的速度脉动情况又会受到外力以及运动边界的影响。当岩屑浓度为2%～8%时，岩屑颗粒具有较高的拟温度，当钻杆转速由100 r/min增加至300 r/min时，岩屑拟温度最大值由122 cm2/s2增加至173 cm2/s2，岩屑拟温度平均值由9.75 cm2/s2增加至11.53 cm2/s2。空心球的拟温度较高的区域主要集中在浓度为2%～12%的区域，当转速为100 r/min时，空心球的拟温度最大值为530 cm2/s2，平均值为68.7 cm2/s2；当转速为300 r/min时，空心球的拟温度最大值为776 cm2/s2，平均值为88.4 cm2/s2。颗粒相的速度脉动主要受到颗粒间的相互作用与流场壁面的影响，颗粒浓度过高的位置表明该处产生了聚集现象，因此颗粒拟温度会随之降低。与此同时，钻杆转速的增加使颗粒相的脉动速度增大，从而导致颗粒拟温度的平均值与最大值相应增大。

图6 不同转速条件下颗粒拟温度随浓度变化情况Fig.6 Variation of granular temperatures with concentration at different rotating speeds

出口截面处颗粒浓度与颗粒流速的柱状如图7所示。由图7可知，当钻杆转速为100 r/min时，出口截面处空心球最大浓度与平均浓度的差值为21%，岩屑最大浓度与平均浓度的差值为5%；当转速增大到300 r/min时，空心球的2种浓度的差值减小为14%，岩屑的2种浓度的差值减小为1%。增加钻杆转速可以提高岩屑与空心球的混合程度，同时使2种颗粒的浓度分布更加均匀，减少颗粒聚集现象。因此，随着转速的增加，颗粒相的最大浓度与平均浓度的差值相应地减小。由图7(b)所示，当转速由100 r/min增加到300 r/min时，2种颗粒的最大流速与平均流速之间的差值随之减小，与此同时，岩屑与空心球的平均流速的差值也随之减小。该趋势表明增大转速可以使2种颗粒的流速更加接近，并且使颗粒在环空井筒中产生更加均匀的流速分布。

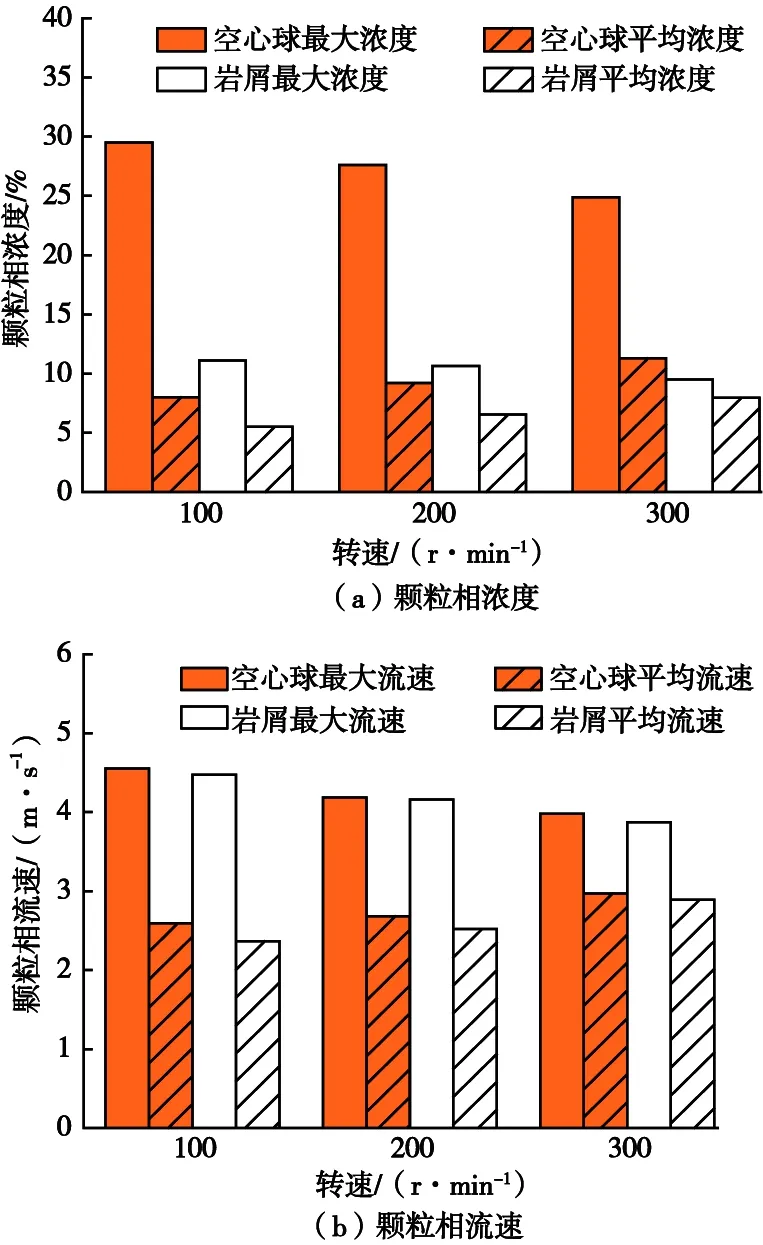
图7 不同转速条件下颗粒浓度与颗粒流速柱状Fig.7 Histogram of particle concentration and particle velocity at different rotating speeds

4 结论

本文采用基于颗粒动理学理论的Eulerian-Eulerian双流体模型，模拟了双梯度钻井过程中岩屑和空心球的流动行为，分析了空心球密度与钻杆转速对岩屑运移情况的影响，得到以下结论。

(1)低密度空心球在注入管线与环空井筒的交界处产生了均匀的过渡区域，该区域对2种颗粒的混合程度起到了促进作用。减小空心球的密度可以有效地降低注入管线上方的混合流体的压降，进而更好地实现双梯度钻井的目的。

(2)提高钻杆转速可以使井筒内颗粒相的速度分布与浓度分布更加均匀，避免岩屑产生堆积现象。与此同时，随着转速的增加，岩屑与空心球的平均流速更加接近，2种颗粒的混合程度得到了提高。研究结果表明，合适的空心球密度与钻杆转速是实现双梯度钻井工况的主要因素。

(3)降低空心球密度有利于改善压力梯度，但空心球注入量以及空心球直径对流场以及压降分布的影响同样值得关注，在今后的研究当中将对上述物性参数展开更加详尽的数值模拟研究。