Model Controlled Prediction: A Reciprocal Alternative of Model Predictive Control

Shen Li, Yang Liu, and Xiaobo Qu,

Dear editor,

This letter presents a reciprocal alternative to model predictive control (MPC), called model controlled prediction. More specifically,in order to integrate dynamic control signals into the transportation prediction models, a new fundamental theory of machine learning based prediction models is proposed. The model can not only learn potential patterns from historical data, but also make optimal predictions based on dynamic external control signals. The model can be used in two typical scenarios: 1) For low real-time control signals (e.g., subway timetable), we use a transfer learning method,so that the prediction models obtained from training data under the old control strategy can be predicted accurately under the new control strategy. 2) For dynamic control signals with high real-time(e.g., online ride-hailing dispatching instructions), we establish a simulation environment, design a control algorithm based on reinforcement learning (RL), and then let the model learn the mapping relationship among dynamic control signals, data, and output in the simulation environment. The experimental results show that the reasonable modeling of control signals can significantly improve the performance of the traffic prediction model.

Unprecedented urbanization has led to the expansion of urban size and density. In order to meet the challenges of mobility and sustainability, more accurate transportation prediction (e.g., passenger flow prediction in public transport systems, spatio-temporal supplydemand prediction in ride-hailing services) is essential to guide the design, planning, operations, and control of urban transportation systems.

Numerous transportation prediction methods based on artificial intelligence (AI) techniques have emerged, such as long short-term memory network (LSTM) [1], convolution neural network (CNN) [2]and graph convolution neural network (GCN) [3]. Unfortunately,most intelligent transportation systems (ITS) are affected by external control signals (e.g., intersection signal timing, metro timetables,online ride-hailing dispatching instructions), while existing traffic prediction methods only mine potential patterns from historical data without introducing control to form a closed loop. Prediction models based on historical data tend to fail or perform poorly as external control signals change.

In order to resolve this critical issue, substantial efforts are conducted to consolidate control and prediction, which are inextricably connected. Therefore, the well-known model predictive control has developed vigorously in enhancing the performance of optimal control, and it has also been applied in numerous traffic control problems [4], but it can not deal with other aspects of transport problems including operations, design, and planning. In the field of ITS, considering the influence of external control signals, the reciprocal alternative of model predictive control has more important and extensive value and has the potential to be applied to all aspects of ITS research.

Related work: Transport engineering is increasingly interdisciplinary with automatic control, AI, and many other emerging areas of information science which form the core of new ITS technology [5].Traffic control and prediction are two important pillars of ITS research.

A representative example in the field of traffic control is intersection signal control, which aims to minimize vehicle travel time by coordinating vehicle movements at road intersections. Since signalized intersection is the bottleneck of urban traffic, effective signal control will reduce traffic congestion [4]. Another example is the railway timetabling control, which has proved to be an NP-Hard problem [6]. Its offline optimization objectives include train travel time [7], total energy consumption [8], transfer waiting time [9], etc.The existing research mainly focuses on mathematical programming [10]. So far, most real-world traffic control strategies are based on offline data optimization, while online rolling optimization has not been implemented. This is due to the complexity and scale of real-world traffic problems, making it difficult to meet the real-time requirements using mathematical programming or heuristic methods.RL has the potential to address this challenge, and few studies have attempted to solve complex large-scale dynamic optimization problems in the ITS field, such as traffic signal control [11] and online ride-hailing fleet management control [12].

Since the emergence of AI and the development of data collection techniques, the application of AI in transportation prediction has affected all aspects of ITS [13]. For example, accurate passenger flow prediction not only helps passengers make better decisions by adjusting their travel routes and departure times, but also helps transit operators optimize train timetables and save operating costs [14].Spatio-temporal data prediction is another core issue, accurately predicting future spatio-temporal supply and demand can help improve traffic conditions, fleet organization, utilization rate, and social welfare. A large number of spatio-temporal data prediction methods based on artificial intelligence techniques have been proposed and applied. Existing state-of-art research is to transform the traffic prediction problem into a regression problem in machine learning.However, these typical traffic prediction problems are affected by the above control signals, but so far, none of these algorithms consider dynamic external control signals. Therefore, it is necessary to develop a new fundamental theory of AI-driven prediction model considering dynamic control.

The fundamental theory of model controlled prediction: As mentioned in the related work, there is no research on integrating dynamic control signals into traffic prediction models. In order to fill the research gap, we will solve three basic scientific research questions.

Q1: Why is Model Predictive Control not applicable to many ITS studies?

Q2: What are the flaws of existing traffic prediction methods compared with model predictive control?

Q3: How can we deal with the flaws in Q2?

Fig. 1 is the illustration of model predictive control. Through Fig. 1,we can analyze and answer Q1 systematically.

The main reasons limiting the application of model predictive control in ITS are:

1) The measurement step in ITS has not been completely solved. It is a challenging task to obtain the travel data of millions of residents in a megacity. In the era of big data and high resolution, the ITS field has only solved very preliminary data acquisition problems. For example, in the bus system, swipe cards in most cities only record the pick-up station, missing the drop-off station. As a result, the measurement step has not yet been completely solved.

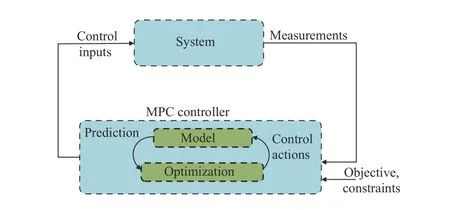
Fig. 1. Illustration of model predictive control.

2) The computational cost of implementing online rolling optimization in ITS is high. Most ITS studies are large-scale and complex (such as optimizing the timetable of the entire city subway line), which are computationally expensive. As a result, these problems are usually optimized offline, and they are difficult to optimize online on a rolling basis.

3) As discussed earlier, ITS systems have numerous applications not only in control, but also in operating, designing, and planning.Compared with transportation prediction, model predictive control has not been able to fully satisfy the diverse requirements of ITS systems, which further limits its wide implementation in ITS.

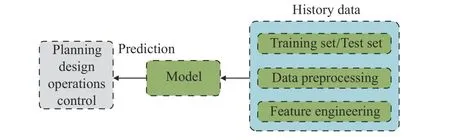
Fig. 2. Illustration of the modeling process of the existing data-driven traffic prediction model.

For Q2, it should be noted that in the existing data-driven traffic prediction models, only data (e.g., dividing training set/test set, data preprocessing, feature engineering), models, and tasks are considered in the modeling process (as shown in Fig. 2), without proper consideration and reflection of the system and optimization.Referring to the illustration of model predictive control, we complete Fig. 2 by adding components such as system and optimization. To distinguish from Figs. 1 and 2, the structure in Fig. 3 is called “control-prediction”. Note that Fig. 3 is a presentation of existing method in the form of model predictive control illustration,where the existing method is flawed. In Fig. 3, although the datadriven model can implicitly learn weak information about external control signals from a large amount of historical data, it is far from sufficient because of the model’s fragility and the inability to respond quickly when external signals change if the model fails to explicitly learn external signals.

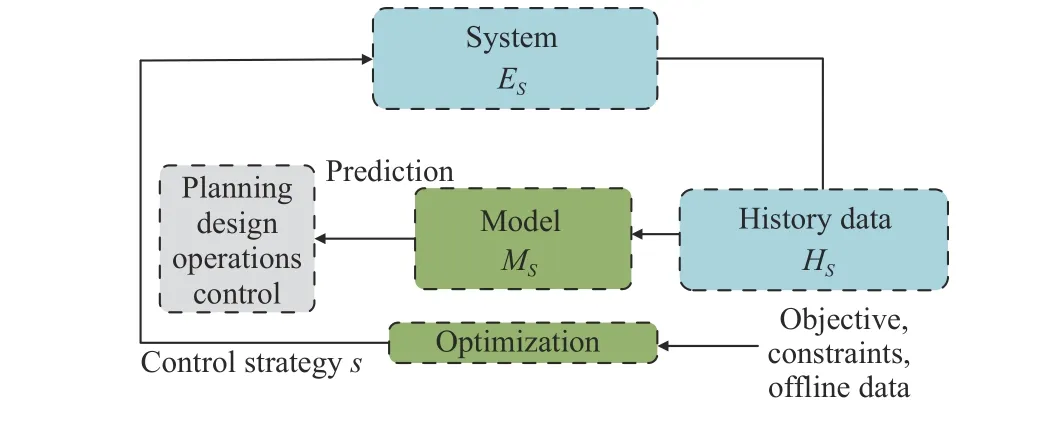
Fig. 3. Illustration of “control-prediction” structure in ITS.

The focus of this paper is on explicitly learning external control signals, and below we briefly analyze the impact of external signals on existing data-driven methods.

The control strategy in Fig. 3 is a time sequence composed of several control signals.

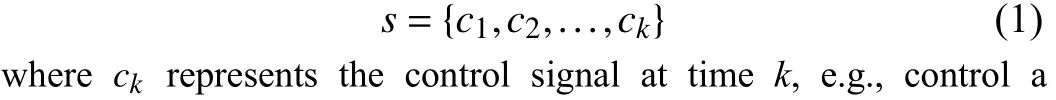
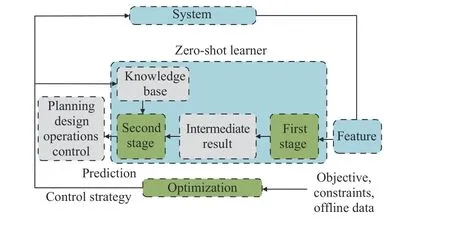
Fig. 4. Flowchart of the zero-shot transfer learner.

The essence of model transfer is to predict another system using the experience learned from the previous system. However, the online car-hailing dispatching algorithm may issue dozens of dispatching instructions per second, which will lead to dynamic changes of the system. Therefore, for these high real-time dynamic control signals, the model transfer approach is not suitable. To address this challenge, we establish a simulation environment, design a control algorithm based on RL, and subsequently let the model learn mapping relationships among dynamic control signals, data,and output in the developed simulation environment. The details of the solution in this situation will be elaborated in Scenario 2.

Fig. 4 shows the flowchart of the zero-shot transfer learner. Based on the developed zero-shot model, the traffic information can be predicted accurately when the control strategy is unknown.

Scenario 2: This scenario deals with high real-time control signals in ITS, which will change in real-time with the change of the system.For example, dozens of online car-hailing dispatching instructions are issued every second. To address this challenge, we establish a simulation environment, design control algorithms based on RL, and then let the model learn the mapping relationships among dynamic control signals, data, and output in the simulation environment, for improving the accuracy of spatio-temporal prediction.

In fact, in general RL, the agent only inputs the current state of the simulator without considering the influence of previous control action on prediction. Whereas in traffic problems, previous control actions can also have a significant impact on prediction results.

For example, the driver’s execution of the dispatching instruction issued by the online car-hailing platform will have a direct impact on the future supply and demand, resulting in a dramatic decrease in the performance of the prediction model. Therefore, we design a RL model with a “recurrent” structure. The term “recurrent” means that the output of the model depends not only on the current computation but also on previous computations, which is similar to recurrent neural networks (RNN) [18].

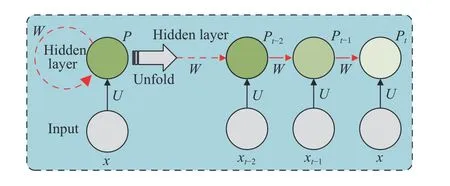
Fig. 5. Illustration of one input unit and one recurrent hidden unit.

In our method (as shown in Fig. 6), the output of the agent depends not only on the current state of the simulator, but also on the previous control actions. We consider the influence of dynamic control signals on the output in the form of “recurrent”.

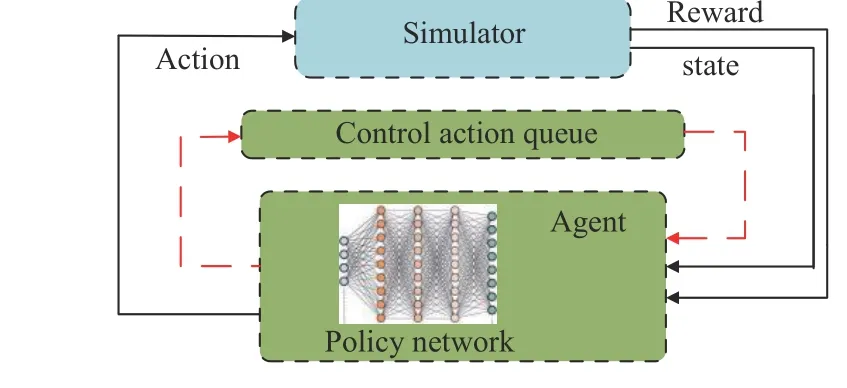
Fig. 6. Illustration of an RL model with “recurrent” structure.

Experiments: Taking the classical passenger flow prediction problem as an example, we conducted a preliminary experiment to verify the hypothesis of this letter, i.e., whether control signals (e.g.,metro timetable) will play a key role in traffic prediction. The data were collected from the Nanjing metro system, including travel records of weekdays from March 18 to April 30 and from August 1 to November 9, 2016. A dataset containing 103 days of records was obtained by denoising, in which the last 33 days of data are the test set, while the rest of the samples were used as the training set. In this case study, the length of the time slice is set to 10 minutes, which means our task is to predict the number of card swipes in the next ten minutes.

We use four evaluation metrics, namely, symmetric mean absolute percent error (SMAPE), root mean square error (RMSE), mean absolute error (MAE), and mean relative error (MRE), to evaluate the performance of the model separately.

The proposed model controlled prediction method is compared with the autoregressive integrated moving average (ARIMA) model and the LSTM model. The parametersp(AR term),d(difference order), andq(MA term) of the ARIMA model are set to 7, 1, and 1 respectively. In the LSTM model, we use the information from the previous four time slices to predict the passenger flow in the next time slice, stacking three LSTM layers to enable the model to learn higher-level temporal representation.

In the model controlled prediction model, based on the LSTM model, we further encode the metro arrival information (i.e., metro timetable) withini-th time slice as a 10-dimensional feature vector.Multiple fully connected layers are used to learn the relationship

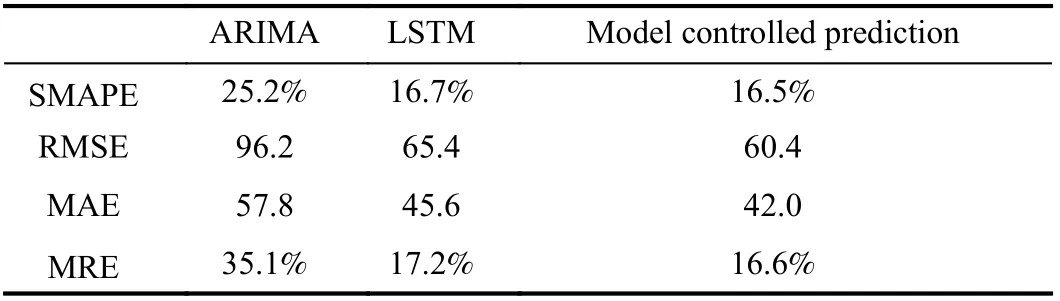
Table 1.Comparison of Different Models (Transfer Station)

Table 2.Comparison of Different Models (Regular Station)

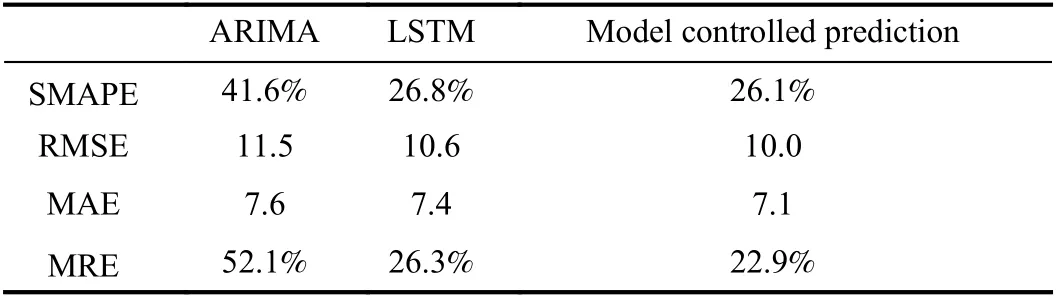
Table 3.Comparison of Different Models (Regular Station With Low Passenger Flow)

Conclusions: The accurate transportation prediction is the foundation for all aspects of ITS, including control, operations,design, and planning. However, most prediction models in ITS do not consider the influence of external control signals (e.g., subway timetables), which compromise the performance, applicability, and transferability of these models. So far, only model predictive control has integrated predictions with external control signals. However,these models are only used for control and not for other aspects of ITS. This research is the first attempt to deal with the most fundamental issue of traffic prediction, considering external control signals, and provide a foundation for ITS applications at all levels.Although the model is developed for ITS, the fundamental theory developed will be sufficiently general to be applicable to other disciplines and systems, provided that the predictions are heavily influenced by external control signals.

In the short term, the research provides a theoretical basis for consolidating predictions and external control signals, thus promoting the scientific development in this area. The theory can also be used in many key use cases, such as the early warning of sudden passenger flow in public transport systems, and the supplydemand balancing in ride-hailing services. In the long run, this research will be even more important in the coming era of connected,automated, and electric vehicles, where the transportation systems,communication systems, and electricity grid are coupled together.This research provides a possible solution for the interactions among different sub-systems in the future urban transportation systems.

Acknowledgments: This study is part of a project that has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie(101025896).