连续梁双曲面球型减隔震支座的数值模拟研究

胡叶江，刘喜仑

(1．中国城市建设研究院有限公司，北京 100120; 2．北京市房山新城投资有限责任公司，北京 102445)

1 概述

多跨连续梁作为高次超静定结构，任何因素的改变都会影响整个桥梁结构的内力和线型，其中合龙顺序就是重要影响因素之一。在连续梁悬臂施工过程中，合龙施工作为一个关键环节，对施工过程、成桥后结构应力以及桥梁线型产生重要的影响，合理的合龙施工顺序确定至关重要，也一直是学者们研究的重点。刘会球[1]就以某铁路专用线(48 +80 +48) m 连续梁桥为工程背景，研究单线铁路连续梁的悬臂浇筑施工合龙方案，通过对4 种不同的合龙方案进行有限元仿真研究，指出合龙顺序对主桥施工过程中应力与挠度以及成桥线形有重要影响。2008 年，任军[2]以堵河特大桥主桥(48 +80 +48) m预应力混凝土连续箱梁的悬臂施工为例，详细介绍了三孔一联的连续梁采用先中跨后边跨的合龙顺序。王学华[3]则对同一座桥梁建立了2 个不同合龙顺序的模型，从施工方案、累计位移和成桥应力3 个方面，对合龙顺序对连续梁桥的影响进行了研究。相比于早期的设计计算而言，现在的桥梁设计工具有很大变化，而这一变化也推动着大跨度桥梁设计技术不断进步。比如，Midas/Civil有限元分析软件的兴起也给大跨度铁路桥梁设计提供了更多样的选择。陈秀清等[4]及徐天良[5]，以Midas/Civil建立有限元模型，分别对预应力混凝土连续梁桥合龙顺序对成桥状态的影响、成桥内力和累计施工位移的影响进行了研究。

与此同时，桥梁支座的发展对有限元软件模拟多跨连续梁的实际状态提出了新的更高的要求。例如双曲面球型减隔震支座在多跨铁路连续梁中的应用就需要对桥梁支座进行更精细的模拟以反映实际状况。刘俊等学者[6]就以有限元分析软件建立了某(48 +4 ×80 +48) m连续梁全桥模型，研究双曲面球型减隔震支座[7-8]在刚构连续梁桥中的应用。目前Midas/Civil 在桥梁设计施工领域有广泛应用，本文拟以某5 跨连续梁桥为实际算例，运用有限元软件Midas/Civil 建立全桥模型，分析双曲面球型减隔震支座在高速铁路多跨连续梁中的应用及合龙顺序对其受力特性的影响，研究结果可供同类桥梁的设计和施工人员参考。

2 工程概况及支座布置

2．1 工程概况

某5 跨连续梁全长477．8 m，计算跨度为(70 +104 +128 +104 +70) m，中支点处梁高为9．6 m，次中支点处梁高为7．6 m，端支座处及跨中截面梁高为5．0 m。梁底下缘按圆曲线变化，圆曲线半径分别为264． 569 m 及400．153 m。边支座中心线至梁端0． 90 m。全联共分115 个梁段，A0，B0 号梁段长度12．0 m，一般梁段分成3．0 m，3．5 m，4．0 m，4．5 m，合龙段长2．0 m，边跨直线段长20．85 m。连续梁桥的立面布置图及标准横断面图见图1，图2。

图1 连续梁桥立面布置图

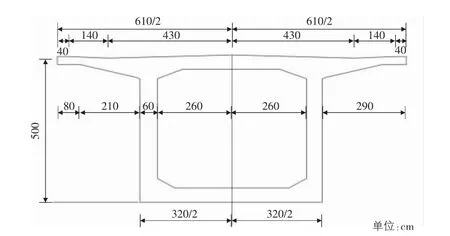
图2 连续梁桥标准断面图

2．2 支座布置

对于多跨连续梁而言，基本的支座布置原则为:1) 梁体在各个方向不能发生刚体位移;2) 允许梁体沿横桥向及纵桥向的自由位移，特别是对于高次超静定结构要允许温度等非荷载因素引起的梁体各个方向的自由变形，否则将会由于多余约束的存在导致梁体内部产生次应力进而造成不利影响。沿桥梁的纵向，桥墩的编号分别为83 号～88 号，桥墩上部支座按照以上原则进行布置，均采用双曲面球型减隔震支座。所谓双球面减隔震支座是指一种具有两个曲面摩擦副，并设置有水平限位板，具备减隔震功能的球型支座。该支座类型不仅具有承受竖向荷载及各项转动的功能，而且具有水平向减隔震功能。双曲面球型减隔震支座的构成见图3。

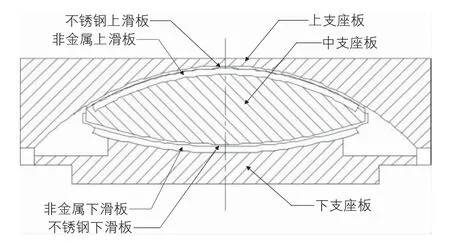
图3 双曲面球型减隔震支座结构示意图

根据JT/T 927—2014 桥梁双曲面球型减隔震支座，设计竖向承载力作用下，支座竖向变形不应大于支座总高度的1%或2 mm 两者中较大者。水平刚度参照设计竖向刚度及经验进行计算，本桥支座布置的对应型号和图纸计算各支座对应的竖向刚度见表1。

表1 支座型号及竖向刚度

3 有限元模型(对支座的模拟)

使用有限元分析软件Midas/Civil 2020 建立5 跨连续梁的数值模型，如图4 所示。全桥模型由199 个节点、174 个单元组成。其客运线路为双线，线间距4．6 m，设计活载为ZK 活载。

图4 全桥有限元模型

连续梁现场进行悬臂浇筑施工，共配置4 套T 构挂篮施工，其中84 号、87 号墩挂篮悬浇施工9(边跨侧为11) 个块段，85 号、86 号墩挂篮悬浇对称施工16 个块段，其合龙方案有两种顺序:

1) 方案一:合龙边跨→张拉边跨部分或全部预应力钢束→拆除临时支座→合龙次中跨→张拉相应预应力钢束→合龙中跨→张拉剩余预应力钢束。

2) 方案二:合龙中跨→张拉中跨部分或全部预应力钢束→拆除临时支座→合龙次中跨→张拉相应预应力钢束→合龙边跨→张拉剩余预应力钢束。

在Midas/Civil 的有限元模型中，可通过建立两个成桥状态相同但施工阶段不同的模型模拟以上合龙顺序，即在相应的施工阶段，激活和钝化相应的梁段、约束及荷载来模拟现场不同的合龙方案，以探究其对支座位移的影响。另外，对于支座的模拟可采用多种连接方式，本研究中为了使模型更加细致且贴合实际，采用了弹性连接中的一般连接类型与刚性连接结合的方式，输入各个方向的支座刚度模拟支座正常使用状态下的特性，值得注意的是，在Midas/Civil 中，弹性连接采用局部坐标系，故其竖向刚度用SDx 表示。图5 为有限元模型中对83 号墩的支座模拟。

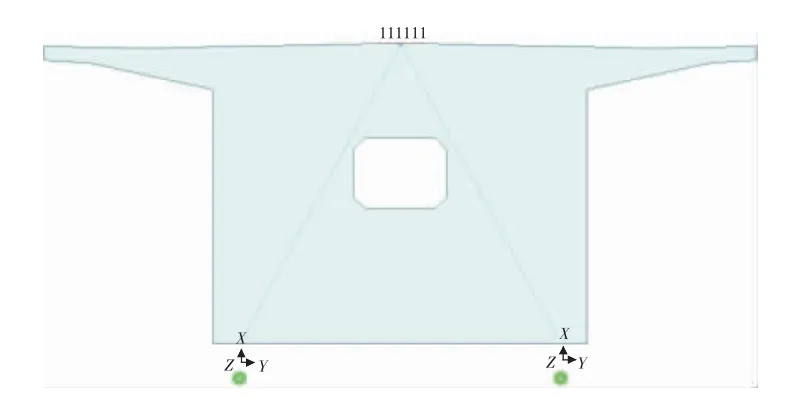
图5 83 号墩支座连接

通过对双曲面球型减隔震支座正常使用状态下受力特性的模拟来研究合龙顺序不同对其受力特性产生的影响。

4 支座受力特性分析

支座的主要作用是承受上部结构荷载，包括恒载及活载，然后将其传递给桥墩/桥台，起到传力的枢纽作用。因此支座的受力特性对整个桥梁结构的受力状态及运营情况起着至关重要的作用。以下以不同合龙顺序工况下支座的支反力、支座位移(包括横向、纵向、竖向) 为研究对象，以研究合龙方案对多跨连续梁支座的受力特性产生的影响。

4．1 支反力分析

支反力分析是多跨连续梁设计中最先要考虑的因素，其直接反映了桥梁的竖向受力状况。由于大跨度铁路连续梁不同支座所提供的支撑作用不同，因此在Midas/Civil 中模拟的约束也不相同，以上已进行过详细介绍，现将不同合龙顺序下各支点处恒载及活载作用下的支反力分布汇总至表2，因长期作用效应下，时间对支反力不产生影响，故此处仅考虑成桥状态下的支反力。

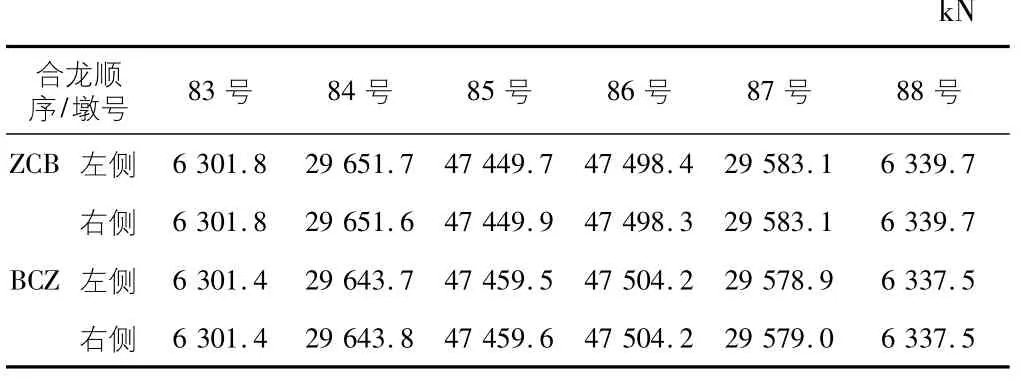
表2 不同合龙顺序下的支反力

由表2 可知，不同合龙顺序下5 跨连续梁成桥状态的峰值边墩、次中墩、中墩的支反力分别为6 339．7 kN，29 651．7 kN，47 504．2 kN，相应型号支座的竖向设计荷载为11 000 kN，40 000 kN，60 000 kN，所有支座的竖向反力均在各型号支座的竖向设计荷载范围之内，满足规范要求且具有一定强度储备，该5 跨连续梁的支座布置合理。

对于次中墩而言，中跨→次中跨→边跨的合龙顺序下其竖向支反力略大于边跨→次中跨→中跨合龙顺序下的竖向支反力，最大差值在8 kN; 对于中墩而言，边跨→次中跨→中跨合龙顺序下的竖向支反力则略大于中跨→次中跨→边跨的合龙顺序下其竖向支反力，最大差值在9．7 kN，但是差值与实际竖向反力相比均不在同一个数量级，因此可以忽略不计，故可以认为多跨连续梁的合龙顺序对其支反力几乎没有影响。

4．2 位移分析

由于混凝土的收缩/徐变效应、预应力钢束的二次效应、温度作用等的影响，支座的变形是一个随时间变化的动态过程，因此对支座各个方向的位移分析需要放在一个较长的时间线上进行考虑。本研究考虑了不同合龙顺序下成桥状态、成桥10 a、成桥30 a 的支座位移变化，从竖向、纵向及横向三个方面进行分析。

4．2．1竖向位移分析

为了使图像看起来更加简洁明了，后文在图像中合龙顺序均使用简称进行表示。中跨→次中跨→边跨的合龙顺序下的成桥状态简记为ZCB-0，边跨→次中跨→中跨的合龙顺序下的成桥10 a 状态简记为BCZ-10，其他状态以此类推。根据表1 确定的各支座竖向刚度及本文采用的双曲面球型减隔震支座正常使用状态下的数值模型，Midas/Civil 可计算桥梁在荷载作用下的各支座竖向位移。将各个桥墩上的支座在不同合龙顺序下各个时间段(成桥状态、成桥10 a 状态及成桥30 a 状态) 的竖向位移进行比较，考虑到横桥向支座竖向位移的对称性，各墩顶见图6，图7。

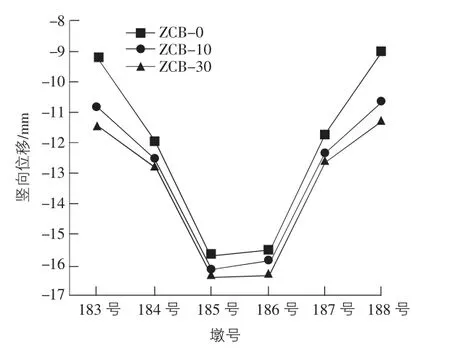
图6 中跨→次中跨→边跨合龙顺序下的支座竖向位移

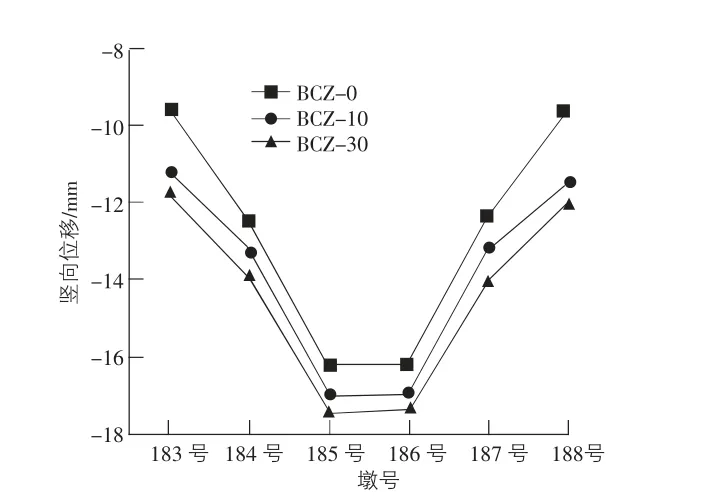
图7 边跨→次中跨→中跨合龙顺序下的支座竖向位移

由图6，图7 可知，对于该5 跨连续梁，无论是哪种合龙顺序，双曲面球型减隔震支座在正常使用状态下的竖向位移均在边墩处最小，中墩处最大。其最小值为中跨→次中跨→边跨合龙顺序下成桥状态，为-9．2 mm;最大值为边跨→次中跨→中跨合龙顺序下的成桥30 a的竖向位移，值为-17．4 mm。之所以支座竖向位移由两边向跨中如此变化是由于中墩处梁高增加而结构自重增大，同时中墩的竖向刚度较大故其承受分配的结构内力也偏大。同时，随着时间的增长，各支座的竖向位移会呈增大趋势，且从成桥状态到成桥10 a 与成桥10 a 到成桥30 a 的支座位移变形相比，支座位移的增长速率下降，这与实际支座的受力状况是一致的，表明该支座的数值模型可以模拟实际支座的时间效应。

此外，对比同一桥墩上不同合龙顺序下成桥状态支座的竖向位移(见表3) ，可以发现边跨→次中跨→中跨合龙顺序下的支座竖向位移均略大于同一时间下中跨→次中跨→边跨合龙顺序下的支座竖向位移，长期时间效应下变化趋势亦是如此，故从竖向位移的角度分析，实际施工时应采用中跨→次中跨→边跨的合龙顺序，可以使得在正常使用状态下支座在竖向具有更多的变形储备。

表3 成桥状态下支座的竖向位移

4．2．2横向位移分析

在正常使用状态下，若不受附加力的影响，实际工作中的支座不受横向扰动时其横向应该处于稳定状态。对于5 跨连续梁的支座横向同样根据规范计算其横向刚度，模拟其横向受力特性。不同合龙顺序长期变形下的支座横向位移汇总见图8。

由图8 可知，在恒载及活载作用下，正常工作状态(不考虑地震等附加作用) 下的支座横向位移最大值仅为-3．4 ×10-5mm，出现在边跨→次中跨→中跨合龙顺序下185 号墩顶支座的30 a 变形工况下，但这一数值相对于其纵向及竖向位移可忽略不计，故可认为使用该支座数值模拟方式可有效模拟支座实际的横向受力状态。

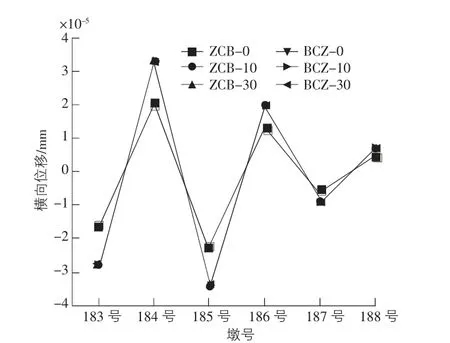
图8 支座横向位移

4．2．3纵向位移分析

支座在正常使用状态下的一大作用就是允许梁体沿纵桥向的自由位移，特别是对于多跨连续梁这种高次超静定结构，要允许混凝土的收缩/徐变特性等非荷载因素引起的梁体沿纵向的自由变形，防止次内力的产生影响桥梁结构的受力状态。因此，对于多跨连续梁不同合龙顺序对双曲面球型减隔震支座在正常使用状态下的纵向位移影响研究至关重要。对于5 跨连续梁的支座纵向同样根据规范计算其纵向刚度，模拟其纵向受力特性。不同合龙顺序长期变形下的支座纵向位移汇总见图9，图10。

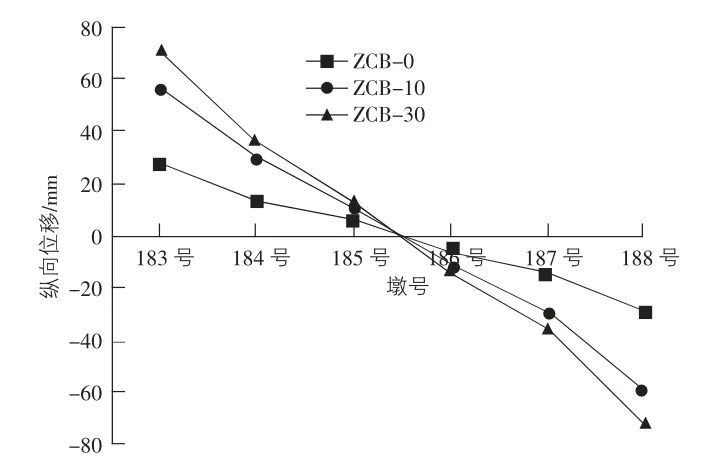
图9 中跨→次中跨→边跨合龙顺序下的支座纵向位移

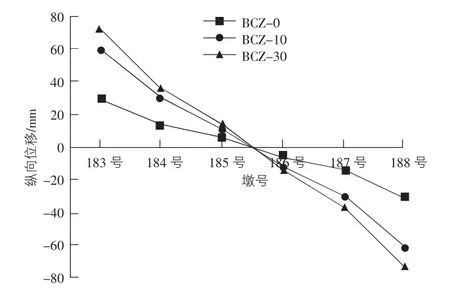
图10 边跨→次中跨→中跨合龙顺序下的支座纵向位移

由图9，图10 可知，对于该5 跨连续梁，无论是哪种合龙顺序，双曲面球型减隔震支座在正常使用状态下的纵向位移均根据跨中对称分布，即支座纵向位移由桥梁两端向跨中收缩变形，这是由于结构沿跨中的高度对称性及材料本身的收缩/徐变及钢束变形等原因导致的，符合实际支座的受力特性，这一特性与合龙顺序无关。

同时，随着成桥时间的增长，同一支座的纵向位移会呈明显的增大趋势，峰值出现在83 号及87 号边墩墩顶。由于各支座纵向位移变化趋势相同，于是以83 号墩顶全部支座不同合龙顺序下的支座纵向位移为例(见表4) 。

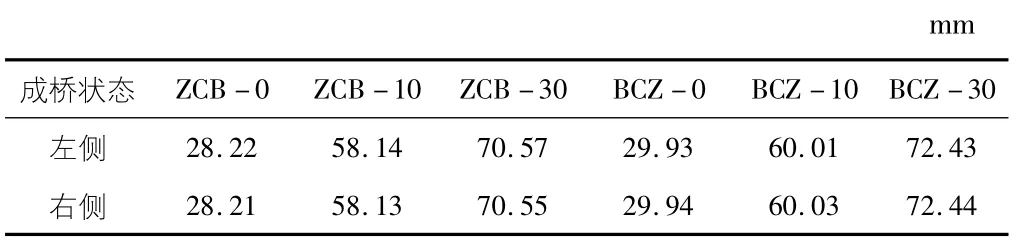
表4 83 号墩顶纵向位移

由表4 可知，随成桥时间增加，从ZCB-0 到ZCB-10 工况时间跨度为10 a，纵向位移增长速率约为2．99 mm/a，从ZCB-10 到ZCB-30 工况，时间跨度为20 a，纵向位移增长速率约为0．62 mm/a，可知支座纵向位移的增长速率同样下降，不同合龙顺序下的变化趋势相同。这与实际支座的受力状况是一致的，表明该支座的数值模型可以模拟实际支座的时间效应。

此外，对比同一桥墩上不同合龙顺序下成桥状态支座的纵向位移，可以发现各个时间点的边跨→次中跨→中跨合龙顺序下的支座竖向位移均略大于同一时间下中跨→次中跨→边跨合龙顺序下的支座竖向位移，长期时间效应下变化趋势亦是如此，故从支座纵向位移的角度分析，实际施工时应采用中跨→次中跨→边跨的合龙顺序，可以使得在正常使用状态下支座在纵向具有更多的变形储备。

5 结论

本文通过对双曲面球型减隔震支座的结构受力性能研究，提出了一种简化且容易实现的正常使用状态下在Midas/Civil 中的数值模拟方式，并以研究5 跨连续梁为例，模拟不同合龙顺序对支座正常受力特性及对时间效应的影响，最终得到以下结论:1)5 跨连续梁成桥状态的边墩、次中墩、中墩的竖向反力均在各型号支座的竖向设计荷载范围之内，各个桥墩的墩顶支座布置合理，受力满足设计要求且具有一定的强度储备。2) 采用弹性连接中的一般连接类型与刚性连接结合的方式，输入各个方向的支座刚度模拟支座正常使用状态下的特性，可以简化模拟双曲面球型减隔震支座的受力特性，算例证明对时间效应及支座各个方向的位移模拟效果良好。3) 各个时间点(成桥状态、成桥10 a 及成桥30 a) 的边跨→次中跨→中跨合龙顺序下的支座竖向、纵向位移均略大于同一时间下中跨→次中跨→边跨合龙顺序下的位移值，长期时间效应下变化趋势亦是如此，故从支座位移的角度分析，施工时应采用中跨→次中跨→边跨的合龙顺序，可以使得在正常使用状态下的支座在各个方向具有更多的变形储备。