SHPB 劈裂试验中FRP-混凝土-钢管的能量耗散分析

翟国良，翟玉鑫，张石磊，张曼丽

(郑州工业应用技术学院建筑工程学院，河南 郑州 451150)

0 引言

经济全球化快速发展，不安定的因素也越来越多。国内外爆炸恐怖袭击事件频繁多发，工业生产中燃油气、危化品爆炸也屡见不鲜，轮船撞击桥墩事件时有发生，车辆撞击桥墩事件经常遇到。为降低爆炸造成的人员财产损失，减小其恶劣社会影响，重要工程结构的抗爆性能亟待提高。

纤维增强复合材料(FRP) 是由增强纤维材料与基体材料经过缠绕、模压或拉挤等成型工艺而形成的复合材料。FRP 材料的出现为解决此类问题提供了有效手段。

FRP-混凝土-钢管构件中的FRP 管具有优越的抗拉和耐疲劳性能，钢管具有较好的抗压抗拉性能。位于FRP 管和钢管之间的混凝土处于三轴压缩状态，套箍作用使构件承载的能力大大提升。具有较强的抗爆和抗冲击能力，对于解决工程中突发荷载具有较深的影响。

2004 年，滕锦光[1]提出一种新的组合柱，在钢管和FRP 中间填充混凝土的新型材料，即FRP-混凝土-钢管组合柱。这种材料具有很多优点，提出后此种材料受到很大的关注。2005 年，徐毅[2]对FRP-混凝土-钢管组合柱抗震的主要因素进行探究，进行了抗震性能的研究，对影响因素进行数值模拟，对影响因素之间的关系建立了数学表达式。2015 年，高丹盈[3]对FRP-混凝土-钢管组合方柱以及其他类型的柱子进行了试验，提出轴压承载力模型，并对其进行验算。2018 年，由河南大学王龙轩、杜文风等[4]对FRP-混凝土-钢组合长柱进行了轴心受压，实验结果表明FRP-混凝土-钢组合长柱构件的强度高于FRP、混凝土和钢管强度总和的30%。各个材料之间的相互作用使材料的优势性能得到发挥，弥补材料的缺点。

1 试验概况

1．1 试件概况

选取不同厚度的FRP 管和不同厚度的钢管，水泥选用海螺牌普通硅酸水泥P．O42．5。控制试件的高径比为0．5，试件高度约为37 mm，直径约为74 mm。制作好的试件如图1 所示。

图1 部分试件

1．2 SHPB 中的能量传递过程

本文试验采用安徽理工大学爆破与冲击动力学研究室直径为74 mm 变截面SHPB 试验装置，如图2 所示。

图2 变截面SHPB 装置

操作气压控制器，将高压氮气瓶的氮气充入高压气室。撞击杆在0．8 MPa 的气压下撞击入射杆。入射杆产生应力脉冲，即入射波ξI(t)，入射波由入射杆应变片搜集，经过系统处理后保存，伴随着巨大的能量，即入射能。入射波到达入射杆与试件接触的端面时，一部分反射回入射杆，即入射波，反射回的能量即入射能; 一部分透过试件传递给透射杆形成透射波，在透射杆中产生的能量即透射能。波通过试件时产生的能量被试件吸收，所产生的能量为吸收能。

为了减少不利因素对试验的影响，得到更加准确的数据。调整入射杆和透射的高度和角度，使撞击杆、入射杆和透射杆轴心在同一水平线上。撞击杆和入射杆接触的端面加黄铜片、折叠的纸张等柔性物质用来降低震荡，从而减小弥散效应[5-6]。试件与压杆之间的接触面涂抹凡士林等润滑剂，可以大大降低摩擦作用消耗的能量[7]。

1．3 能量耗散的基本原理

霍普金森压杆中的应力传播示意图如图3 所示。SHPB 压杆实验及其实验结果分析都建立在两个基本假设上:1) 一维应力波假设。2) 均匀性假设[8-11]。

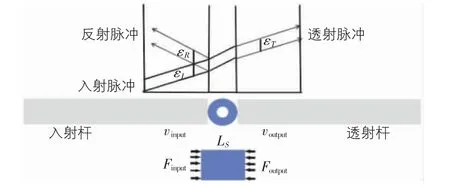
图3 SHPB 装置及应力波形图

在这个假设的基础上推导“三波法”和“二波法”公式。假设入射杆与试件的接触面为输入面，透射杆与试件的接触面为输出面，输入面的力和速度为Finput和Vinput，输出面的力和速度为Foutput和Voutput，根据线弹性波的叠加原理，力和速度的公式如下所示:

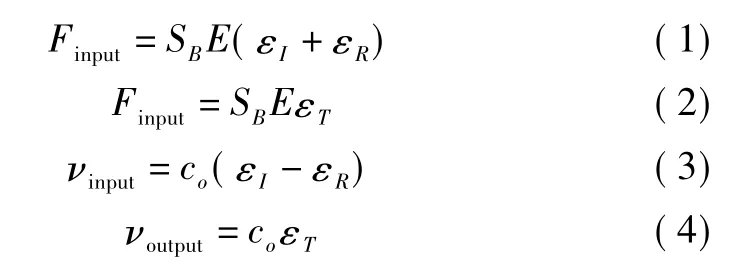
其中，Finput，Foutput，νinput，νoutput分别为左右接触面的力和速度;SB为压杆的截面面积;E为压杆的弹性模量;co为压杆的弹性波波速;εI，εR，εT分别为试件的入射应变脉冲、反射应变脉冲、透射应变脉冲。

根据霍普金森压杆的第二个假设，用两端的速度差计算压缩应变率如式(5) ，将式(3) 和式(4) 代入式(5)可得:

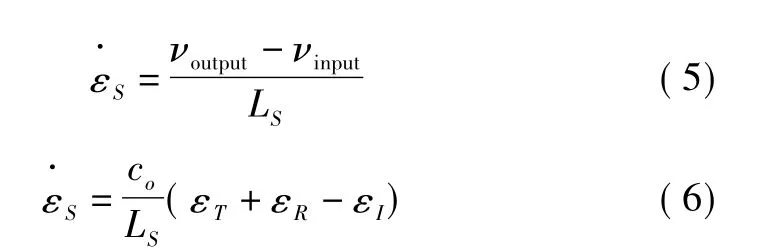
其中，LS为试件的长度。

根据霍普金森压杆，将压缩应变率式(6) 积分可得到压缩应变式(7) :

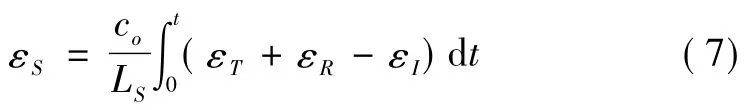
根据压强定律可得式(8) ，将式(1) 和式(2) 代入可以得到应力:

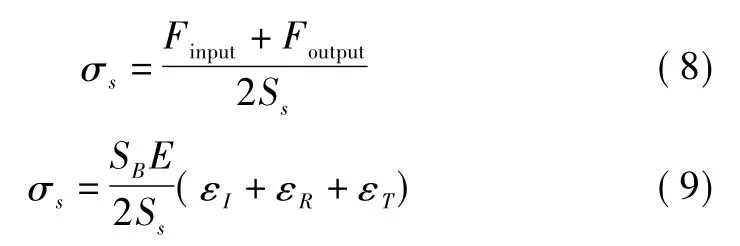
其中，Ss为试件的截面面积。

得到的式(6) 、式(7) 和式(9) 即“三波法”公式。

基本假设下，组合结构有均匀的应变，则有εI+εR=εT，将其代入“三波法”公式中可得“二波法”公式，即式(10) 、式(11) 和式(12) :

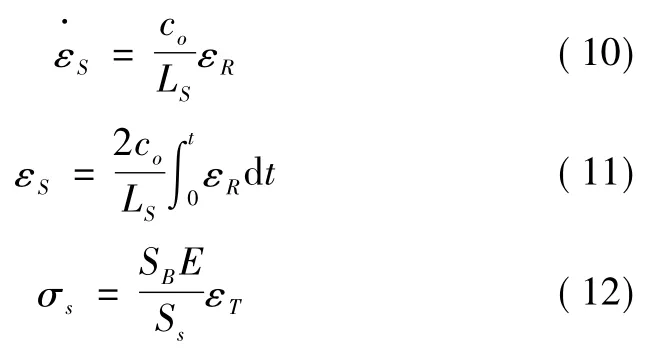
将试件的参数代入可得本次试验公式。

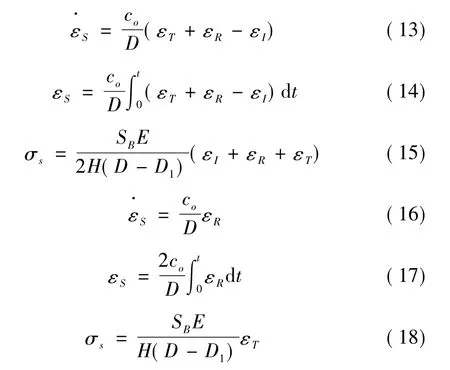
其中，D为试件外径;D1为试件的内径;H为试件的高度。

根据动态力学实验中能量耗散分析的理论公式[12-15]，通过对入射、反射和透射应变脉冲分别积分计算后可以得到入射波能量、反射波能量和透射波能量。

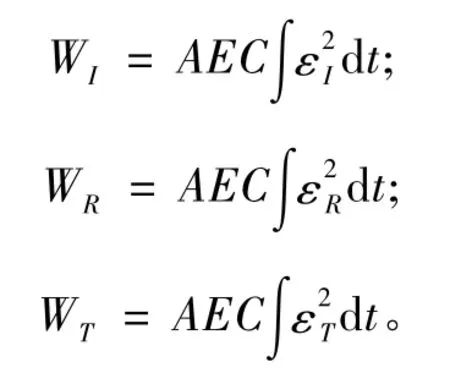
其中，A为入射杆和透射杆横截面面积;E为入射杆和透射杆材料弹模量;C为应力波在杆中的传播速度;εI，εR，εT分别为试件中的入射、反射和透射应变脉冲。

试件破坏的过程中产生的碎块飞出，部分能量转化为动能。根据金解放等[16]对SHPB 动力学试验研究，能量耗散分析结果发现试件的动能只占吸收能非常小的一部分，可以忽略不计。当动能及其他能量忽略不计时，此时根据能量守恒定律可知，入射波能量、反射波能量、透射波能量和试件吸收能量的关系为:

WS=WI-WR-WT。

其中，WS为试件吸收能量;WI为入射波能量;WR为反射波能量;WT为透射波能量。

为了更好的探索多次冲击下试件的吸收能力的情况，引入定义吸收能系数(Energy absorption coefficient)η的表达式。

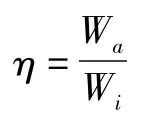
其中，Wa为试件的吸收能;Wi为试件的入射能。

2 试验结果及分析

将数据代入计算公式，求得计算结果如表1 所示。

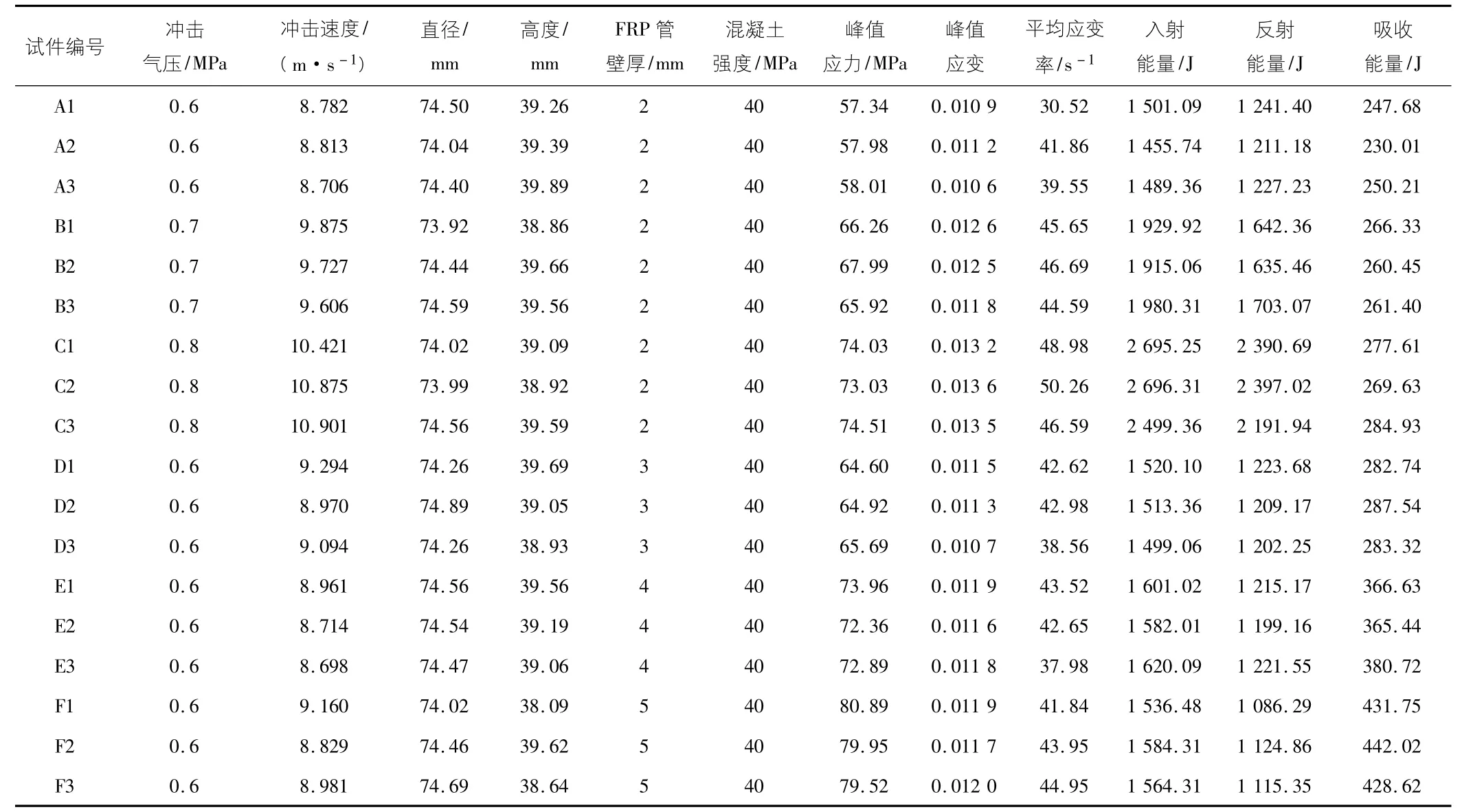
表1 试验结果表

2．1 典型的能量变化时程

选取试块A 为典型的研究对象，用0．6 MPa 的气压对试块进行冲击，分析能量的变化过程，能量的变化过程如图4 所示，并结合图5 试块的应变过程进行分析。

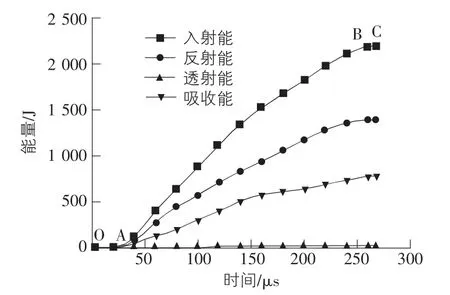
图4 能量变化时程图

对试块的能量和应变在不同时间的变化情况进行研究，结合图4，图5 可以发现，能量的变化过程和应变变化过程出现同步发展的趋势;在50 μs ～250 μs 时间段内，能量和应变的增加相对稳定; 透射能随着时间的增加并不明显，具体分析过程如下:

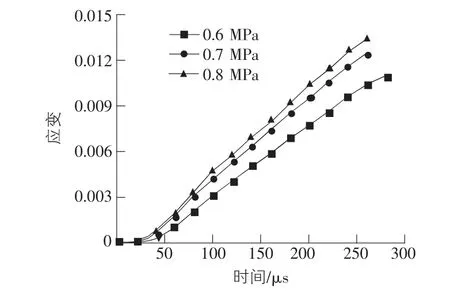
图5 应变随气压变化的过程图

第一阶段OA 段，0 μs ～50 μs，在气压的作用下，撞击杆将能量传递入射杆中，此部分能量为入射能;能量通过入射杆和试块交界面后，一部分能量反弹回入射杆中，此部分能量为反射能;能量进入试块后，试块吸收的部分为吸收能，进入透射杆的能量为透射能。能量的传递时间间隔较短，入射能、反射能、透射能和吸收能呈现同步增长的趋势。此时间段能量增长缓慢，试块的变形也缓慢，试块的变形和能量的增加需要一个过程，在这个过程中，试块逐渐被挤密。

第二阶段AB 段，50 μs ～250 μs，此时的能量和应变的能加量相对稳定，相同的时间增加量变化不大。在此作用下，试件中的应力重新达到一个稳定的状态;新状态下能量和变形稳步增加。

第三阶段BC 段，250 μs 以后，此时的能量和变形基本无变化，试块和压杆脱离接触，能量的增加和试块的变形基本结束。

2．2 冲击速度的影响

用不同的速度冲击相同条件下同批制作的试块，运用控制变量法研究冲击速度和能量之间的关系，对冲击速度和能量进行曲线拟合，得到的关系如图6 所示。

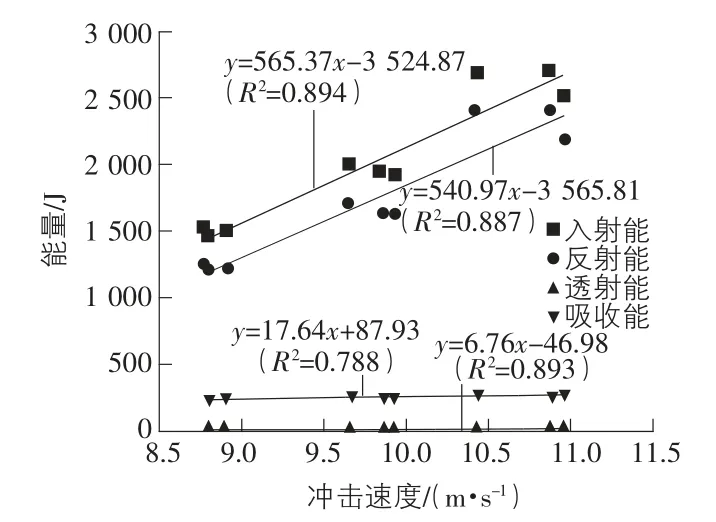
图6 速度与能量关系图

用不同的速度进行冲击，冲击速度的增加使能量同步增加，两者是正相关且呈现线性增加的趋势，入射能和反射能的增加速度比较快，透射能的增加影响较小。试块和压杆之间是径向接触，这种接触办法使得杆件和试块接触面积比较小，造成能量传递过程中的大部分能量反弹回去; 小部分能量进入试块，进入试块的能量大部分被试块吸收，吸收的能量造成试块变形，混凝土产生裂纹，甚至块状脱落; 最后的一小部分能量进入透射杆中。冲击速度增加带来较多的能量，对能量的分布影响不大。

2．3 破碎形态

研究不同气压作用下试块的破碎形态，分别用0．6 MPa，0．7 MPa，0．8 MPa 对一号试块、二号试块和三号试块进行冲击，各个试块在冲击作用下的破碎形态如图7 所示。

图7 不同气压作用下的破碎形态

气压每增加0． 1 MPa 的时候，裂纹就会增多，甚至会出现块状脱落。气压的增加会使冲击速度同步增加，试块吸收较多能量造成变形加快，从而产生和杆件轴心垂直的裂纹和块状脱落，试块的破碎就会加重，破坏程度加深。

3 多次冲击的能量耗散分析

3．1 能量变化时程

1) 多次冲击下反射能变化过程。

将同一试件进行四次冲击后的反射能变化过程绘制成曲线。反射能时程曲线如图8 所示。

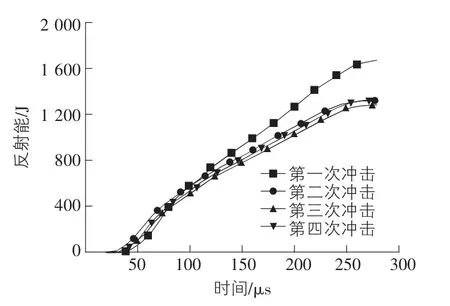
图8 多次冲击的反射能时程曲线

由图8 可以看出，第一次冲击时反射能比较高，第二次、第三次和第四次冲击时反射能降低并且保持稳定。这是由于第一次冲击后试件发生变形，试件与压杆的接触面积增大，通过试件的能量增多，从而导致入射能降低; 第一次冲击后试件处于稳定状态，变形和应力分布没有较大的变化，因而反射能变化不大。

2) 多次冲击下吸收能变化过程。

将多次冲击的吸收能随着时间的变化绘制成图像，吸收能时程曲线如图9 所示。

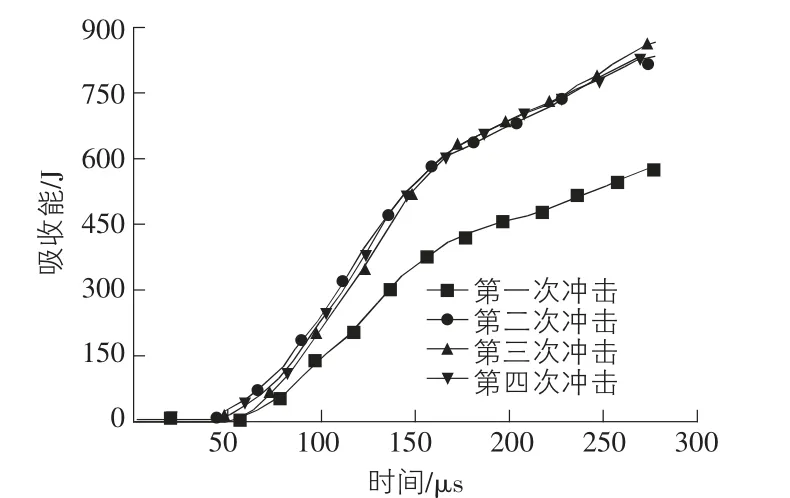
图9 多次冲击的吸收能时程曲线

由图9 可以看出，第一次冲击时吸收能比较低，第二次、第三次和第四次冲击时吸收能升高并且保持稳定。这是因为第一次冲击后试件中的混凝土产生裂纹，并且带有轻微的破碎，使试件的吸收能增加;混凝土受到FRP管和钢管的约束，试件具有较强的抵抗冲击的能力，在0．8 MPa 冲击气压下混凝土破碎程度增加不大，试件变形情况亦不明显，导致第二次、第三次和第四次吸收能量基本保持一致。

3．2 FRP 管壁厚与能量

研究FRP 管壁厚与能量之间的关系，采用相同的加载条件，获得的入射能存在较小的差异，以及其他因素对试验结果造成影响。对入射能、吸收能与FRP 管壁厚之间的关系，采用反射能与入射能的比值、吸收能与入射能的比值和FRP 管壁厚之间的关系。

选取第四次冲击后的能量耗散进行分析。冲击后的能量数据如表2 所示。

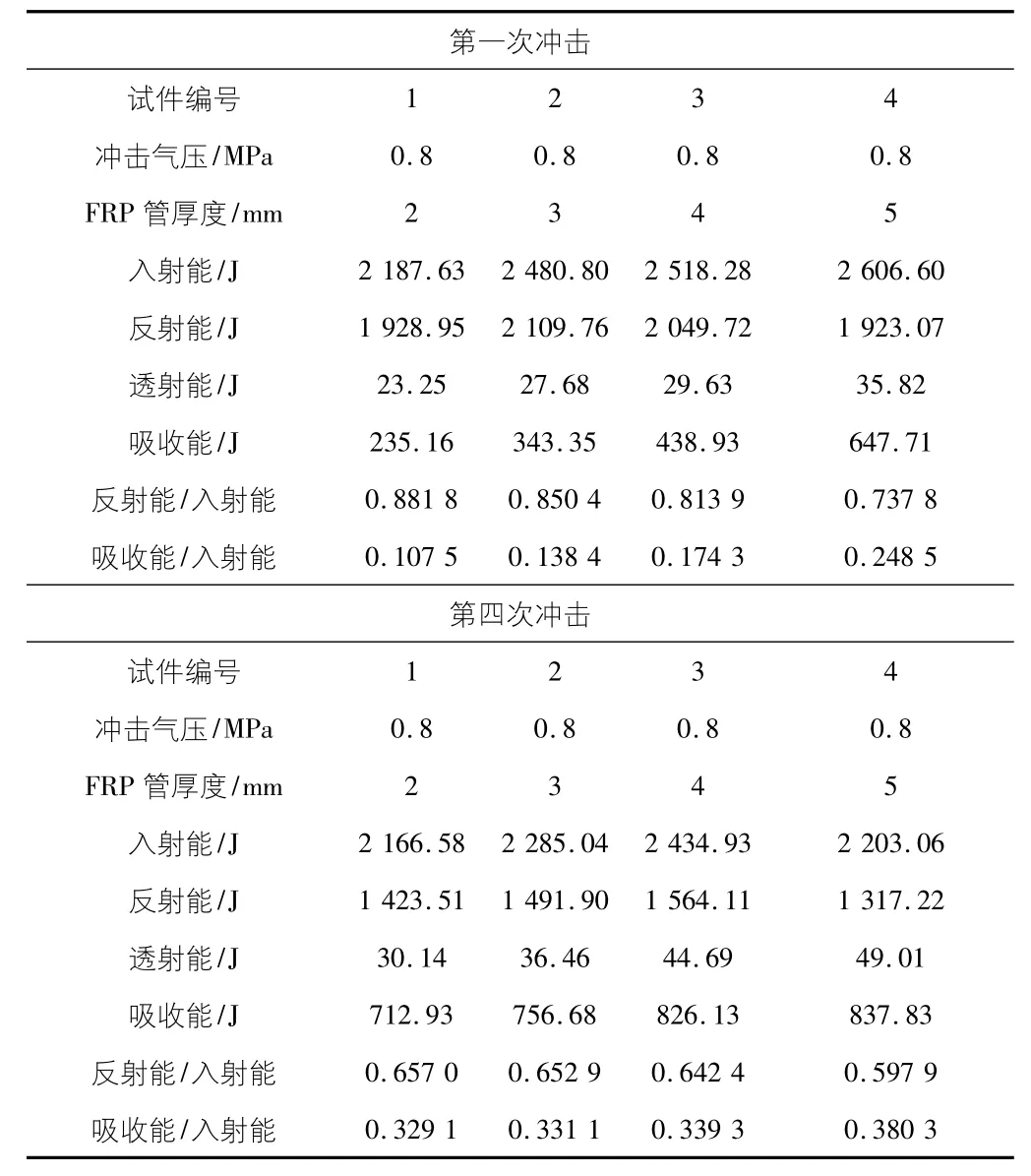
表2 试验结果

1) 第一次冲击能量比值与FRP 管壁厚。

对第一次冲击后的能量进行曲线拟合，拟合后的结果如图10 所示。

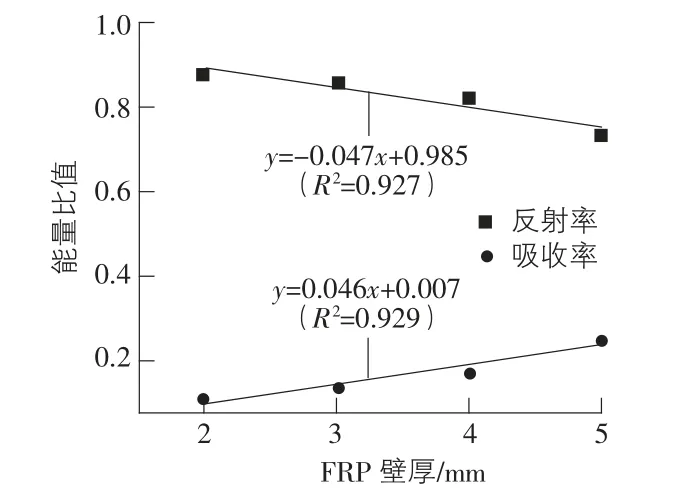
图10 第一次冲击能量比值与FRP 管壁厚关系曲线

由图10 可以看出，在入射能相同的条件下，反射能随着FRP 管的厚度增加呈线性减少，吸收能随着FRP 管厚度的增加呈线性增加。对两者的关系进行曲线拟合，拟合后的表达式如下所示。

这是因为混凝土属于脆性材料，FRP 管有较好的延性，FRP 管吸收能量的能力比混凝土强。FRP 管厚度每增加1 mm，相应的混凝土厚度减少1 mm，随着FRP 管厚度的增加，吸收能逐渐增加。

2) 第四次冲击能量比值与FRP 管壁厚。

对第四次冲击后的数据进行分析，拟合的曲线如图11 所示。

由图11 可以看出，在入射能相同的条件下，反射能随着FRP 管的厚度增加而下降，下降的速率越来越快，吸收能随着FRP 管厚度的增加而增加，增加的速率越来越快。对两者的关系进行曲线拟合，拟合后的表达式如下所示。

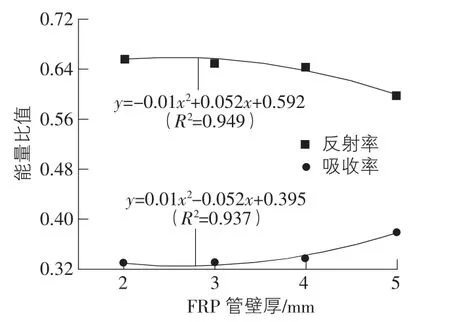
图11 第四次冲击能量比值与FRP 管壁厚关系曲线

原因是试件经过四次冲击，试件中的混凝土遭到破坏，吸收能力增强; 根据第一次冲击可知FRP 管的吸收能量的能力比较好，从而造成吸收能随着FRP 管厚度的增加逐渐增加加快。

3．3 多次冲击的破碎分析

在相同的条件下用0．8 MPa 的气压对试块进行多次冲击，研究多次冲击作用下试块的破坏情况。破碎形态如图12 所示。

图12 多次冲击作用下的破碎形态

试验使用的FRP 管壁比较厚，对里面的混凝土保护能力较强，历经多次冲击作用后，破坏程度没有明显增强，增加了少量裂纹，没有出现块状破坏。这表明试块处于三轴围压作用下[17-18]，可以大大提高混凝土抵抗破坏的能力，使试块的承载能力增强。

4 结语

通过试件的冲击劈裂实验，对试件能量耗散规律进行分析研究，得到如下结论:

1) 第二次、三次和四次冲击后，峰值应力、应变曲线、入射能曲线和吸收能曲线基本相同。第一次冲击之后，冲击次数的增加对峰值应力、应变、入射能和吸收能基本没有影响。

2) FRP 管吸收能量的能力比混凝土强。第一次冲击时，FRP 管和吸收能量、入射能呈线性关系。第四次冲击，加上混凝土破碎的因素，FRP 管和吸收能量、入射能呈一元二次方程的关系。

3) 对破碎形态进行分析可以得到，气压的增加可以带来较多的能量，从而使试块的破坏加深; FRP 管壁厚的增加可以更好的保护内部结构，降低对试块的破坏。