可燃气体爆炸极限的理论预测方法研究

吴华杰，孙云厚，郑 磊，秦 凯

(军事科学院国防工程研究院，北京 100850)

1 概述

可燃性气体爆炸已经逐渐成为工业生产、日常生活以及军事国防领域中重要的危害之一，每年因可燃气体爆炸而造成的经济损失巨大，甚至造成人员伤亡的惨痛代价，因此，开展可燃性气体爆炸机理研究，掌握爆炸过程特征规律，对预防可燃性气体爆炸具有十分重要的意义，而爆炸极限条件是研究可燃性气体爆炸的一个重要内容。已有研究结果表明: 如果爆炸性气体的浓度处于一定的爆炸极限范围内，则在外界的荷载作用条件下就会导致爆炸的发生，对于不同的气体混合系统或者同一混合系统处于不同的环境下，它的爆炸极限不是一个固定值，而是受爆炸压力等多种因素交织影响的，因此，在工业生产中很难定量确定可燃/可爆气体的安全温度压力范围和极限值。但是，如果对可燃混合气体的爆炸极限先进行理论计算，通过分析得到大量数据，之后，通过一定的算法(比如机器学习支持向量机(SVM) 算法) 对通过理论分析得到的数据进行预测，进而研究并找出可燃性气体混合系统发生爆炸的规律，精确地描述整个爆炸发生过程，就可有效地提出针对性的减灾防灾的预警机制、应急预案、灾害处置和恢复的措施方案，最大程度的降低因爆炸而引起的多重反应所造成的人员和财产损失。

可燃气体的爆炸是一个非常复杂的物理、化学过程，涉及多门学科的综合理论知识。爆炸的发生有三个必须条件:可燃物、助燃物和点火源[1-4]。目前，对于可燃混合气体的爆炸条件研究主要采用物理和化学模型试验的方式，利用取得的试验数据，采用一定的假设条件，通过理论分析得到的定性或者部分定量的描述规律，由于试验数据样本有限，这些规律存在一定局限性。随着计算机技术的不断发展和应用，利用机器学习算法对混合气体进行预测分析是一种有效的方法。目前，针对混合气体的极限条件的理论预测方法有基团贡献法、神经网络法、化学平衡法、绝热火焰温度法、F-number 分析法、Le-Chatelier 公式法、Taylor 多项式拟合法等。近年来，马秋菊等基于热平衡方程及混合气体的各组分浓度、淬灭电势及燃烧潜热，提出一种针对“可燃气体+ 惰性气体+氧气”混合可燃气体的爆炸极限预测模型。李国梁等，通过计算绝热火焰温度法对部分可燃碳氢化合物与氮气混合后的爆炸极限进行了预测。熊中浩等[5]根据试验测得的混合气体的组分及爆炸极限，结合Le-Chatelier 法可以得出由组分计算混合气体爆炸极限的方法并编成软件，经验证，该软件计算得到的爆炸极限与实验值的误差小于10%。田兰等[6]整理和汇总了前人研究得到的可燃气体爆炸极限数据、曲线。

综上所述，已有的研究成果主要集中在对可燃气体混合物爆炸效应的分析上，而对爆炸极限的理论预测则很少，这主要是因为通过理论预测是非常困难且烦琐的，目前缺少通用的理论预测模型，未能建立针对性强的计算机算法。本文以氢气-氧气混合系统为例进行研究，通过对整个系统的化学反应速率方程分析，建立特征矩阵，为计算模型的验证提供数据池;基于爆炸极限的理论分析计算得到大量数据，再通过机器学习SVM 算法对获取的数据进行计算预测。通过对氢气-氧气系统发生爆炸的极限条件的算法预测，得到较好的预测效果，验证了本文模型的准确性与可靠性，可为军事和民用工程的气体爆炸安全预测预警提供理论支撑，也可为可燃气体的爆炸应急预案制定提供指导。

2 氢氧爆炸极限特征值分析

作为典型的混合气体系统，氢气-氧气混合气体是工业、医疗、市政等各个领域使用最多的混合气体形式之一，由于其具有很强的化学活性、渗透性以及扩散性，在氢气与氧气的混合系统中，在满足其他条件的情况下，既可以被日常生活中的明火点燃，也可以被一些“暗火”条件，比如气流中包裹的固体颗粒、物理撞击与机械环境中的静电放电火花点燃。氢的发生点火的能级很小(约为0．019 mJ) 。

试验结果表明，对于氢气-氧气混合的气体系统，发生爆炸除了满足点燃温度条件外，还需要满足氢气浓度达到一定条件，这就是氢气浓度的极限值，而这个极限值与气体压力条件密切相关，中国工程物理研究院王建等[7]通过采用爆轰管试验的方式，通过不同的疏密条件，以爆炸压力、波速在燃烧向爆轰转化的瞬间所发生的数值突变作为判断爆炸的极限条件值。其实验结果得出爆炸压力随着氢气密度增加呈现倒“U”字形的变化，并得出氢气的最佳爆炸浓度值为体积分数值50%; 而对于常温常压条件，氢气的爆炸临界体积分数为15% ～90%(即上限为90%，下限为15%) ，此数值与杨金翠等[8]给出的上下限分别为94%与4%的结论基本一致，同时还得出氢气和氧气的混合气体发生爆炸的临界压力为0．01 MPa。但这些均限制于特定的温度和压力条件，而对于不同的温度压力条件，需要构建更加准确的预测理论，建立不同的预测模型，才能更好指导科学实践。

对于氢气-氧气混合系统，各气体组分的反应过程、反应速率是影响爆炸发生的重要因素，是分析系统发生爆炸条件的理论基础。王贤明等[9]以矩阵形式给出了组分H，O，OH，HO2，H2O2的反应速率方程:

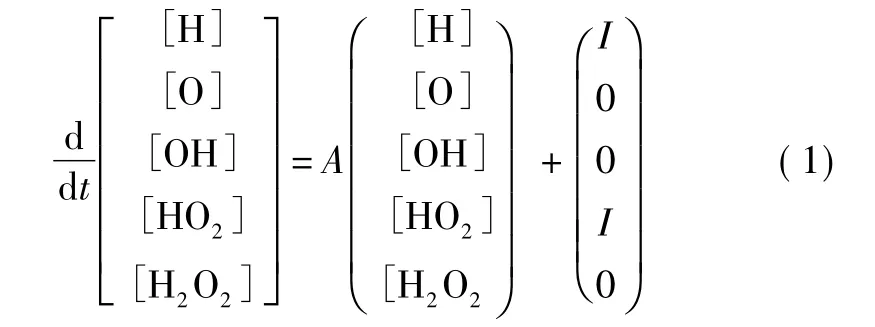
其中，I=kl[O2][H2]，是链引发反应H2+O2→HO2+H 的反应速率矩阵。

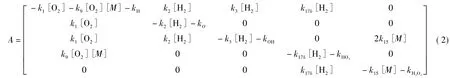
其中，[M]为摩尔浓度。对于这样一个线性系统，是否发生爆炸取决于系数矩阵A的特征值的实部数值。如果任意一个特征值的实部均为正数，则表示中间浓度的矩阵值会随时间变化呈指数增长，导致相应支链爆炸的发生。否则，就不会发生爆炸。因此，界定温度-压力图中爆炸区域和非爆炸区域的边界爆炸极限条件可以由函数ξ(T，[M]) =0 给出，这个条件与ξ(T，p/(R0T) ) =0相当，其中，ζ为特征值的最大实部。这就为混合系统爆炸极限条件预测提供了界定的条件。

3 支持向量机算法工况分析

对于上游获取的大量甚至海量的数据池，如何准确进行分析，给出相应的规律，是机器学习的使命，而科学合理的算法则是这一切的核心。Sklearn 软件包是一个十分方便的软件包，可用于琐碎的科学机器学习编码工作，另外，采用Sklearn 软件包还可以用来实现二元分类任务的支持向量机算法(Support Vector Machine，SVM) 。

支持向量机是一个经典的二分类算法，其找到的分割超平面具有更好的鲁棒性，因此广泛使用在很多任务上，并表现出了很强优势。对于一个给定的二分类器数据集D={(x(n)，y(n)}N(其中，n=1，yn∈{ +1，-1}) ，如果两类样本是线性可分的，则存在一个超平面将两类样本分开:

对于给定的训练数据集xi∈Rp，yi∈{1，-1}n，i∈N，其中yi为相关xi的预分类，SVM 算法的任务即是找到参数集ω∈Rp和b∈R，使sgn(ωTφ(x) +b) 给出的预测满足大多数验证结果。

针对前述氢气-氧气混合系统的爆炸工况，作为一个快速回燃条件，通过支持向量机算法的计算可以对氢气-氧气混合系统的爆炸极限变化趋势进行演示验证。图1 给出了H2混合物的爆炸极限值随H2，O2以及惰性气体混合比例的变化趋势图(其中图1(a) 为采用H2∶O2比的函数变化趋势图，图1(b) 为采用惰性比的函数变化趋势图) 。从图1 可看出: 在压力-温度变化曲线图上，无论是采用H2∶O2比的函数形式，还是采用惰性比的函数形式，随着压力的不断增大，爆炸分界温度均呈现反向“S”形变化趋势; 另一方面，采用惰性比函数形式得到的数据离散性要比采用H2∶O2比形式的要稍微大些，同时两个反“S”变化的拐点值也存在一定差异，前者拐点位置的压力要高于后者，而拐点温度要低于后者，这说明采用不同的预测函数形式，对于最终的预测结果将会产生一定程度的影响，但总体变化趋势是一致的。

根据前述预测算法理论，依据图1(a) 中的数据，通过支持向量机算法可得到其SVM 能力的测试图(如图2所示) ，图2 中实线代表从图1(a) 数据收集到的确切值，根据实线可以随机生成左右两类不同的散点。其中，左侧数值为利用SVM 做出的预测，背景覆盖浓度表示置信程度，浓度越浓表示SVM 对这里的数据分类越有把握。从图2 中分析可看出:本文采用SVM 算法预测得到的结果与期望值吻合较好，证明了此预测模型的可靠性，保证了支持向量机进一步应用的可行性。

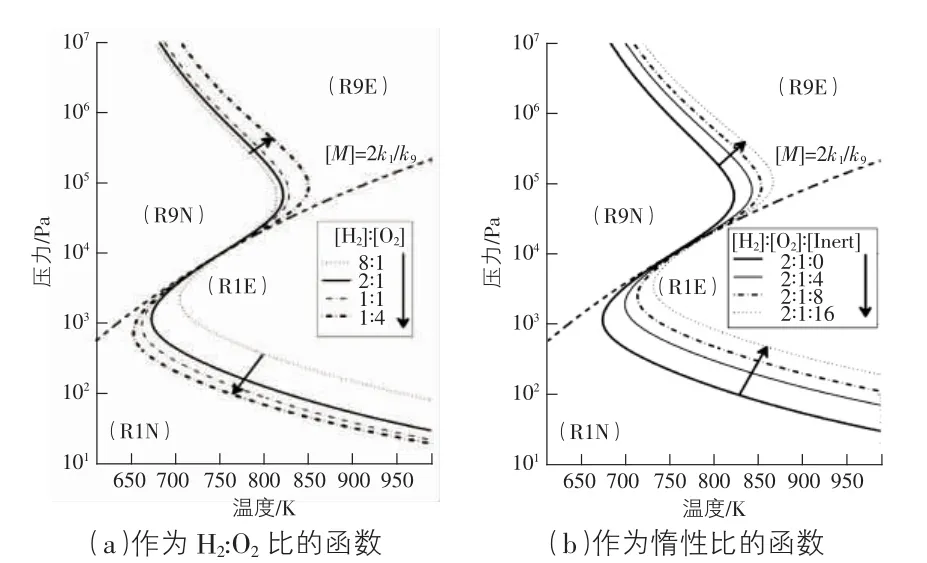
图1 不同混合比下H2 混合物的爆炸极限

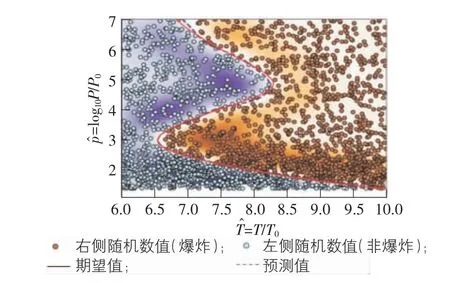
图2 SVM 的能力测试

图3 为根据不同混合比下氢气-氧气混合系统的爆炸极限预测图，分别表示H2∶O2=1∶4，1∶1，2∶1 与8∶1 四种情况。为获得更好的数值性能，T轴和P轴采用无量

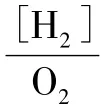
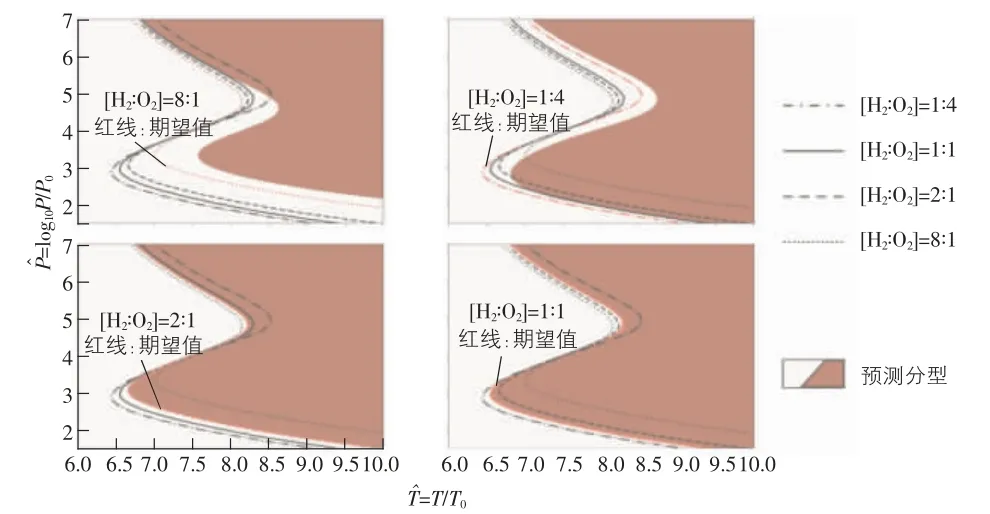
图3 不同混合比下H2-O2 混合物的爆炸极限

比值参数按比例缩放:

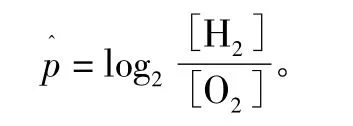
从图3 的预测结果可看出: 在本文的预测理论基础上，采用支持向量算法的外推和内推在机器学习中存在差异，其中8∶1 和1∶4 的情况是外部情况，即外推情况;另外两种情况是插值情况结果。预测结果和期望值之间的比较告诉我们，即使只有3 个训练集，SVM 也可以非常准确地预测插值情况。

4 结论

本文通过对氢气-氧气混合气体爆炸条件的分析，基于混合气体爆炸极限理论的反应速率方程，对氢气和氧气混合系统，采用H2与O2比与惰性气体比两种不同的混合比例函数变化趋势，验证了采用支持向量机算法的正确性; 在此基础上，采用不同预测函数形式，通过计算机神经网络算法得到了不同混合比下氢气-氧气系统爆炸极限边界预测结果，与期望值吻合很好。得出的主要结论如下:

1) 采用支持向量机(Support Vector Machine，SVM) 算法可以较为准确地预测气体爆炸极限范围。

2) 无论是采用H2∶O2比的函数形式，还是采用惰性比的函数形式，随着压力的不断增大，爆炸分界温度均呈现反向“S”形变化趋势。

3) 采用惰性比函数形式得到的数据离散性要比采用H2∶O2比形式的要大，两种情况的反“S”变化的拐点值也存在一定差异，前者拐点位置的压力要低于后者，而拐点温度则要高于后者。

4) 对于不同混合比的气体，即使只有3 个训练集，支持向量机(Support Vector Machine，SVM) 算法也可以非常准确地预测插值情况，表明采用深度计算机学习能够比较准确地内推和外推爆炸极限带宽。

5) 由于目前的数据集模板较少，所以对于混合气体系统，内推和外推在机器学习预测结果与理论值的差异，预测结果则还需进一步优化。军事工程和民用工程领域中可燃气体是典型的爆炸形式，一旦发生爆炸，将会产生无法挽回的生命和财产损失，因此，建立科学合理的爆炸极限条件预测模型，开展系统的研究，找到爆炸发生的条件规律意义重大。本文通过理论分析，结合机器学习方法，对SVM 算法进行的预测结果比对，验证了本文模型的科学性与可行性，可为混合气体的爆炸风险等级评估、安全预防提供更好的预测方案和理论支撑。