炮位侦校雷达高精度弹道外推技术研究
严军,刘奇涛
(1.南京电子技术研究所,江苏 南京 210000;2.西北机电工程研究所,陕西 咸阳 712099)
炮位侦察校射雷达的主要作战使命是对敌方炮位的侦察和己方火炮的校射,通过快速有效地完成火力侦察支撑快速打击任务,在现代战争中发挥着重要的作用[1-5]。炮位侦校雷达通过搜索发现弹丸目标进行跟踪,然后进行弹道处理外推炮位和落点。弹道外推的精度决定着炮位侦校雷达的性能,而运动模型直接影响弹道外推的精度。国内外传统的炮位侦校雷达数据处理方法通常基于重力平面模型,忽略了其他因素对弹道的影响,因此仅适用于中、近程火炮的侦察校射。近年来,随着各种远程火箭弹、增程弹技术的突飞猛进[6],平面重力模型已不能很好地满足精度需求,迫切需要采用高精度弹道模型。
1 弹道模型研究
1.1 理论模型
箭弹的运动受力非常复杂,精确的计算需要同时考虑质心和姿态的运动[7],这需要知道很多弹体相关的先验信息,对于箭弹的外弹道设计来说可以进行详细的考虑,但是对于炮位雷达非合作目标的弹道外推来说,雷达观测条件的限制决定了只能对质心运动进行近似的考虑,因此炮位侦校雷达中通常广泛地采用简化的弹道方程描述弹丸质心的运动。
1.1.1 平面运动模型
传统炮位侦校雷达的数据处理为了简化计算,不考虑地球曲面的影响,采用了简单的平面模型,并在平面模型中将地球引力取为常值,同时考虑大气阻尼和风的影响。其运动方程如下[8-9]:
(1)
1.1.2 考虑地球曲率的运动模型
弹丸是在地球表面的空间运动的,弹丸在运动过程中的地心引力是指向地心的,由于地球表面是复杂的曲面,因此作用在弹丸上的地心引力指向随着弹丸运动不断变化。为了更好地描述弹丸的运动,应当选择在地心直角坐标系中描述弹丸的运动,一般可以选择常用的WGS84坐标系,相应的运动模型如下[10-11]:
(2)

1.1.3 考虑地球自转的运动模型
平面模型和考虑地球曲率的模型忽略了地球的自转,实际情况下地球是存在自转的,地球自转会产生离心力和柯氏力。考虑到这些力的影响后,在WGS84坐标系下,相应运动模型如下:
(3)
式中,we为地球自转角速度。
1.1.4 考虑地球J2引力的运动模型
地球不是完美的球体,更准确地描述应该是一个定扁率的椭球体,这导致地球引力对弹丸的影响在质心引力外存在附加引力,其中最大的一项为J2项非球形引力。对于弹丸的运动来说,只需要考虑J2项非球形引力就足够了,相应的运动模型如下:
(4)
式中:J2为地球非球形引力系数;ae为地球赤道半径。
1.2 仿真分析
为了比较上述不同模型的差异,选取一射程为35 km的弹丸进行仿真,仿真中采用相同的初始条件,比较不同模型预报的轨道差异,仿真参数如下:
炮位位置:经度45°,纬度45°;
射角:35°;
射向:45°;
初速:1 000 m/s。
1.2.1 地球曲率的影响分析
图1给出的是上述仿真条件下,采用平面模型和考虑地球曲率的运动模型,轨道预报结果在地心直角坐标系中3个坐标分量的差异。

可以看到,在给定的仿真条件下,采用平面模型和曲面模型,位置预报差异可达50 m左右。
1.2.2 地球自转的影响分析
图2给出的是上述仿真条件下,采用球面模型和同时考虑地球自转的运动模型,轨道预报结果在地心直角坐标系中3个坐标分量的差异。

可以看到,考虑地球自转和不考虑地球自转,预报结果差异在150 m量级。
1.2.3J2项引力的影响分析
图3给出的是上述仿真条件下,采用考虑地球自转的运动模型和同时考虑地球J2项引力运动模型,轨道预报结果在地心直角坐标系中3个坐标分量的差异。

可以看到,考虑地球J2项引力和不考虑地球J2项引力,预报结果差异在30 m量级。
2 参数估计方法
建立弹道运动方程后,为了进行弹道外推,首先要进行弹道参数估计。由前面的介绍可知,目标运动方程是非线性的,观测方程一般也是非线性的,因此是一个非线性参数估计问题。炮位雷达探测目标时获得的观测数据带有误差,常用的非线性参数估计方法有最小二乘估计、扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)和粒子滤波(PF)等[12-14]。通过参数估计得到弹道目标的运动参数,利用弹道运动方程采用成熟的数值积分方法即可进行弹道外推,获得炮位和落点等参数。
2.1 最小二乘拟合
最小二乘估计是一种常用的参数估计方法,以预测数据与观测数据的残差平方和最小为目标函数来进行未知参数估计。假设测量值Z与估计参数X满足关系:
Z(j)=h(j,X)+V(j),j=1,2,…,
(5)
式中,V(j)为测量噪声。
参数估计结果X(k)为使得k次观测拟合残差平方和达到最小的解,即

(6)
炮弹飞行轨迹可以近似为一抛物线,首先利用雷达测量数据对抛物线的参数进行最小二乘估计,然后用估计得到的参数曲线即可外推算出弹丸发射点或落点。
2.2 扩展卡尔曼滤波
2.2.1 状态方程
取x,y,z,vx,vy,vz,c作为卡尔曼滤波的状态变量。
(7)


(8)
f(θ)的具体表达式由选择的运动模型决定,该非线性方程只是目标真实运动模型的近似,有一定误差,为了补偿这个误差,引入一个模型噪声W,则变为

(9)
式中,W为零均值高斯白噪声,W~N(0,Q)。
2.2.2 观测方程
设雷达量测值为斜距R,方位角β,高低角ε,雷达球坐标与直角坐标之间的转换方程为
(10)
令观测矢量Z=(R,β,ε)T,则有
Z=h(θ)+V,
(11)
式中:V为雷达测量噪声,假定为零均值高斯白噪声,V~N(0,R);h(θ)为三维矢量函数:
(12)
2.2.3 扩展的卡尔曼滤波器
设离散化的量测噪声Vk有如下均值和方差:
E(Vk)=0,
(13)
(14)
离散形式的状态扰动Wk有如下均值和方差:
E(Wk)=0,
(15)
(16)
扩充的卡尔曼滤波方程:
1)预测方程为
(17)
2)预测协方差为
(18)

3)观测量预测方程为
(19)
4)滤波方程为
(20)
式中,Wk+1为加权矩阵,
(21)
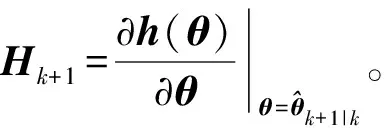
5)滤波协方差:
Pk+1=[I-Wk+1·Hk+1]·Pk+1|k.
(22)
通常EKF是逐渐收敛的过程,滤波终点的参数估计精度高于中间点,一般采用滤波终点的参数进行弹道外推,为了使外推距离更短,可以从数据末点开始进行反向滤波,有利于提高精度。
2.3 各种方法比较
参数估计方法中,最小二乘估计是一种常用的传统方法,由于无法估计弹道系数等其他弹道参数,外推精度相对较差,它的优势是在数据点很少的情况下依然可以得到外推结果。
EKF算法计算量较小,但是需要计算雅可比矩阵,对于复杂的非线性方程,雅可比矩阵的计算比较复杂。EKF算法适用于弱非线性问题,在非线性较大的场景,可能会出现滤波发散的情况。
除了上面的方法,无迹卡尔曼滤波(UKF)算法和粒子滤波(PF)也被应用到弹道参数估计中。UKF算法适用于各种非线性高斯噪声问题,计算量比EKF大,对非线性问题的适应性更好,其滤波精度和外推精度都比较好。PF算法由于需要采样大量的粒子,计算量明显较大。对于高度非线性问题,这两者较EKF方法有一定的优势,但对于火箭弹的弹道外推来说,非线性程度还无法体现两者的优势,采用EKF、UKF和PF没有本质区别。
3 结束语
弹丸在运动过程中受到多种力的影响,通过建立考虑不同因素的运动模型,采用相同初值进行轨道预测并比较。仿真表明,在给定仿真条件下,地球曲率的影响在50 m左右、地球自转的影响在150 m左右、J2项引力的影响都在30 m左右。对于射程更远的弹丸,这些力的影响可能更大,随着装备的发展,这些力的影响不可忽略,需要进行考虑。

