基于整数权重的非二进制SAR ADC及其校准算法的设计

刘宇航，曹晓东，张雪莲，张其鑫

（1.中国科学院半导体研究所，北京100083；2.中国科学院大学，北京100049）

基因测序专用芯片是基因测序仪的核心部件之一，模数转换器作为基因测序专用芯片的关键电路模块，其转换精度直接影响了基因测序仪的性能.

半导体制造过程中的电容失配会引起SAR ADC 转换精度降低，需要采用校准算法计算并存储电容失配值，通过融合ADC 转换结果与电容失配值，获得满足精度要求的ADC 输出信号.文献［1］提出了一种结合扰动信号注入的校准方式，其中DAC电容阵列中每一位电容均采用sub-radix-2（亚二进制）的分数电容，由于各个分数电容之间相互独立，因此难以形成匹配.文献［2］采用温度计编码方式实现了一款10 bit SAR ADC 结构，其编码方式需要较多控制电路，会增加电路的复杂性［3］.文献［4］通过采用伪随机序列获取电容阵列中的误差信息，由于需要多个伪随机序列才能获得所有电容的误差信息，因此会大大增加电路成本.文献［5-6］提出了一种用于SAR ADC 的拆分型（Split）校准方法，该模数转换器在校准时需要生成多个不同的决策路径，并且比较器和一些控制电路将会倍增.文献［7］提出一种基于扰动的SAR ADC 数字校准算法，其采用上极板采样的方式会引起电荷注入的问题从而影响采样精度，并且其采用单调开关时序，不是最节省功耗的方式［8］.

针对以上问题，本文作者提出了一种基于整数权重的非二进制SAR ADC 及其校准算法.在校准模式下，基于自适应LMS 算法进行迭代优化以获得最佳的电容权重，校准结束后，将所有权重的最终值进行保存，并在正常转换模式时结合ADC 的量化结果得到最终的14 位二进制输出码.ADC 电容阵列采用基于整数权重的非二进制编码的分段电容阵列，以解决sub-radix-2 编码中分数电容匹配性的问题.为了避免上极板采样带来的电荷注入问题，本文通过下极板进行采样，并且电容阵列下极板电压的切换方式采用开关时序来降低功耗损失.

1 LMS 算法原理

ADC 的工作模式包括校准模式和正常转换模式，图1 所示为校准模式下数字校准算法的流程图，校准模式主要包含以下四步.

1）首先对输入的模拟信号进行采样，并对采样到的模拟信号值V1加入正负扰动信号±Δa，采样信号加入扰动后的模拟信号值记作V1±Δa.

2）模拟信号值V1±Δa经过ADC 量化后得到十进制输出分别记作D+和D-

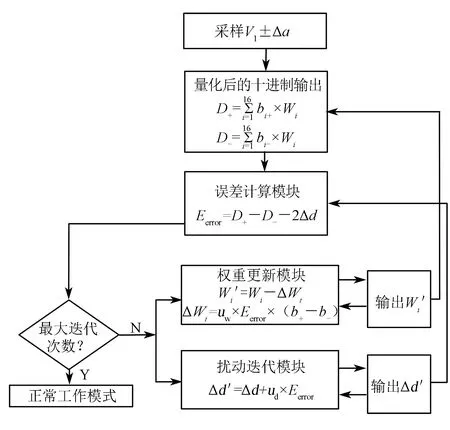
图1 校准算法流程图Fig.1 Flow chart of calibration algorithm

式中：bi+、bi-（i=0，1…，n）是量化后的二进制编码；Wi为电容权重.将正负注入的模拟电压值±Δa对应数字域量化值表示为±Δd.

3）将带有正负扰动注入的输入信号进行量化后的结果D+和D-输送到误差计算模块.理想情况下，D+和D-在数字域上的差异应该是2Δd，但是由于电容失配和寄生效应等非理想因素的存在，使得D+和D-存在偏差，用Eerror来表示

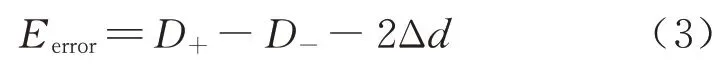
4）为消除上述偏差，采用基于LMS 迭代算法优化每一位的权重.将Eerror分别输入到权重更新模块和扰动迭代模块，得到更新后的权重值W′i和扰动值Δd′

式中：uw和ud为迭代的步长，其值根据收敛速度、精度折中选取.

将更新后的权重和Δd′返回到第三步的误差计算模块，得到更新后的Eerror值.循环执行图1 所示的步骤，直到达到最大迭代次数，校准结束，得到并保存权重的最佳值，ADC 进入正常转换模式，将转换值与保存起来的各比特权重的乘积作为ADC 的最终输出.本文所采用的校准算法的扰动注入仅由两个注入电容和简单数字逻辑构成，其复杂度明显低于分离式模数转换器校准方式［5-6］，也比基于基准ADC 的校准方式简单［9］.

2 电路结构及工作原理

2.1 非二进制权重SAR ADC 电容阵列设计

传统Sub-radix-2 的非二进制编码虽然可以使输入输出特性曲线出现非单调特性，引入冗余量，提供消除转换过程中动态误差的方法，但其电容阵列采用分数电容，会带来电容匹配性的问题.为解决以上问题，本文设计的DAC 电容阵列采用整数编码方式，既可以达到与Sub-radix-2编码同样的效果，又可以解决由Subradix-2 编码引起的电容匹配性问题.图2 所示为14 位逐次逼近型模数转换器结构图，该结构采用全差分输入方式，其中，Vin和Vip为模拟输入信号，Vcm为共模电平，Vref为基准电压，高段电容阵列由权重电容Ch1～Ch8以及扰动信号注入电容Ctp和Ctn构成，高段电容阵列为采样电容，采样阶段时下极板接输入信号.低段电容阵列由权重电容Cl1～Cl13以及接固定电位的电容Cl0构成，Cb为桥接电容.下面将对低段权重电容和高段权重电容下极板电压的切换对上极板电压产生的影响分别进行分析.

图2 14 位逐次逼近型模数转换器结构图Fig.2 Structure diagram of 14-bit SAR ADC

当低段权重电容下极板电压切换时，如图3 所示，其中CLSB为低段电容阵列总体电容值，CMSB为高段电容阵列总体电容值，Cli为进行下极板电压切换的低段权重电容（i=1，2，…，13）.当Cli下极板电压进行切换时，在Cli下极板引起的电压变化值是∆Vref，此时其他电容下极板不进行切换，引起的下极板电压变化值是0，认为其等效接地.因此，可以得出由Cli下极板切换产生的电压变化值∆Vref和由它引起的上极板电压变化量Vx之间的关系为

图3 低段权重电容下极板电压的切换简图Fig.3 Switching diagram of the lower plate voltage in lowsegment weight capacitor

当高段权重电容下极板电压切换时，如图4 所示，其中Chi为进行下极板电压切换的高段权重电容（i=1，2，…，8）.当Chi下极板电压进行切换时，在Chi下极板引起的电压变化值是∆Vref，此时，其他电容下极板不进行切换，引起的下极板电压变化值是0，认为其等效接地.因此，可以得出由Chi下极板切换产生的电压变化值∆Vref和由它引起的上极板电压变化量Vx之间的关系为

图4 高段权重电容下极板电压的切换简图Fig.4 Switching diagram of the lower plate voltage in highlevel weight capacitor

由于扰动信号的注入电容Ctp和Ctn位于高段电容阵列中，所以扰动信号大小可以根据式（7）进行计算.将式（7）中的电容值Chi替换成扰动信号的注入电容Ctp/Ctn即可得到扰动信号值.

若按照二进制电容阵列的编码方式，低段电容阵列有6 个权重电容，容值分别是2 C，4 C，8 C，16 C，32 C，64 C，高段电容阵列应有7 个权重电容，容值分别是2 C，4 C，8 C，16 C，32 C，64 C，128 C，但为设计满足校准算法的基于整数权重的非二进制编码结构，本设计所采用电容阵列的编码是基于电容权重的缩放重组方式，将低段电容阵列最高位电容64 C 进行拆分，拆分成42 C，8 C，4 C，2 C，2 C，2 C，2 C，2 C，将高段电容阵列最高位电容128 C 进行拆分，拆分成127 C 和C，将拆分后的电容按照表1 中的排列方式放入图2 所示的电容阵列中，由于该缩放重组的方法没有改变总的电容值，因此SAR ADC 可量化的输入信号范围不受拆分电容的影响.表1 中所示各个权重电容的权重值比例可按照式（6）和式（7）中分子的比值进行计算即可，桥接电容Cb=4 C.从表1 中可以看出，高位电容的权重值均小于其低位电容权重值之和，满足亚二进制的关系，电容阵列具有很好的冗余特性，因此若高位出现比较错误，可以通过低位的比较将其纠正回来.

表1 14 bit桥接结构非二进制权重冗余CDAC阵列电容设计Tab.1 Design of 14-bit bridge-structure non-binary weight redundant CDAC array capacitor

2.2 基于LMS 的结合扰动信号注入的校准方案

图5 为数字校准算法的时序图，整个ADC 的工作过程分为校准模式和正常转换模式.校准模式下，采样时钟clks 的频率是正常工作模式时采样时钟clk的一半.校准模式分为6 个阶段，包括采样阶段、正扰动信号的注入阶段、带正扰动注入的采样信号的量化阶段、扰动信号复位阶段、负扰动信号注入阶段、带负扰动注入的采样信号的量化阶段.数字校准模块通过获得注入正负扰动后的量化结果进行误差计算，并通过LMS 算法对误差进行迭代，等待LMS 算法收敛，校准模式结束，进入正常转换模式，将校准模式下得到的最佳权重保存下来，用于正常转换模式.正常转换模式分为3 个阶段，包括采样阶段，保持阶段和量化阶段.正常转换模式，将比较器输出结果与校准后的权重加权求和，并且截取高14 位作为ADC 的最终数字输出结果.

图5 基于扰动的数字校准的时序图Fig.5 Timing diagram of disturbance-based digital calibration

由于SAR ADC 采用上极板采样会带来电荷注入的问题，电荷注入直接影响采样精度，从而影响ADC的转换精度.为解决以上问题，本设计采用下极板采样，下极板采样可以通过时序控制来解决电荷注入的问题，并且电容阵列下极板电压切换采用Vcm_based开关时序来降低功耗损失.校准模式和正常转换模式下电路的工作时序和电容极板切换方式如下.

1）校准模式.

采样阶段，即t1～t2时间段内，只需对每个采样信号值采样一次.电容上极板接共模电平Vcm，低段电容阵列的电容下极板接Vcm，高段阵列电容下极板接采样信号Vi.

正扰动信号的注入阶段，即t2～t3时间段内，电容阵列上极板首先与Vcm断开，P侧电容阵列中扰动注入电容Ctp下极板接参考电压Vref，N侧电容阵列中扰动注入电容Ctn下极板GND，其余所有电容下极板接Vcm.

带正扰动注入的采样信号的量化阶段，即t3～t4时间段内，第一次比较时不需要进行电容阵列的切换，直接进行第一次比较，根据比较结果决定P侧和N侧电容下极板的接法.若比较器P侧输出结果Voutp=1，则P侧电容由Vcm切换到GND，N侧电容由Vcm切 换 到Vref；若Voutp=0，则P侧 电 容 由Vcm切换到Vref，N侧电容由Vcm切换到GND.如此反复执行直到所有比特位量化结束.

扰动信号的复位阶段，即t4～t5时间段内，将Ctp和Ctn下极板接Vcm，使采样信号的值恢复到正扰动信号注入之前即Vi.

负扰动信号的注入阶段，即t5～t6时间段内，将Ctp下极板接GND，Ctn下极板Vref，其余所有电容下极板接Vcm.

带负扰动注入采样信号的量化阶段，即t6～t7时间段内，电容下极板切换方式同正扰动信号注入时量化阶段的切换方式.

如上所述为校准模式下一个完整的量化周期，不断对输入信号进行采用并量化，将正负注入的量化结果输入到数字校准模块中，按照图1 所示的流程执行，直到达到最大迭代次数，校准模式结束，进入正常转换模式.

2）正常转换模式.

在采样阶段，即t8～t9时间段内，电容上极板接Vcm，低段电容阵列（Cpl0～Cpl13）下极板接Vcm，高段阵列电容下极板接Vi，整个电容阵列存储的电荷量为

在保持阶段，即t9～t10时间段内，上极板首先与Vcm断开，然后所有电容下极板均接Vcm.保持阶段，整个电容阵列存储的电荷量为

根据电荷守恒，由式（8）和式（9）可以得到

在量化阶段，即t10～t11时间段内，电容下极板的切换方式同校准模式下量化阶段的切换方式.结合量化阶段的切换方式，以及比较器输出结果Di，可以得到Vx在整个转换过程中的通用表达式为

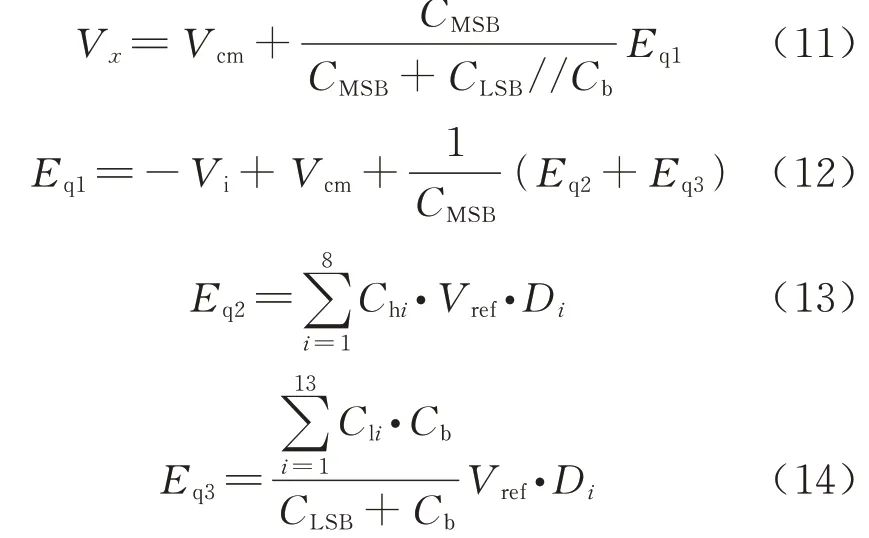
将比较器输出结果Di与校准后的权重加权求和得到校准后的14 bit 数字输出码.

3 非理想因素分析

除电容失配外，时钟抖动、KT 噪声、比较器噪声、寄生电容等均会对SAR ADC 的系统性能产生影响，本节通过考虑主要模块的非理性特性，给出带有非理想因素的SAR ADC 的建模方式.

3.1 采样保持电路建模

采样保持电路用来将模拟输入信号按照相应的采样时钟进行采样或保持，作为模数转换器的重要模块，其性能影响整个ADC 的精度和速度.对整个采样保持电路的建模主要包括时钟抖动建模、KT噪声建模两部分［10］.

3.1.1 时钟抖动建模

假设Δt为时钟的抖动，输入信号为IN(t)，那么由时钟抖动产生的偏差可以表示为

其模型如图6 所示，其中In 模块为理想正弦输入信号.

3.1.2 KT 噪声建模

KT 噪声可等效为白噪声，如果采样开关在导通时其等效电阻为Ron，采样电容为Cs，那么此时导通电阻的噪声频谱密度可以表示为

开关热噪声的总噪声功率为

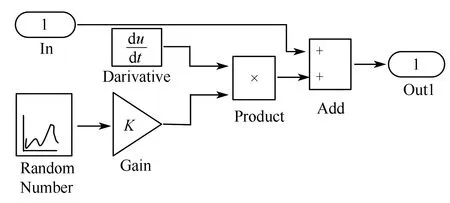
图6 采样时钟抖动建模Fig.6 Sample clock jitter modeling

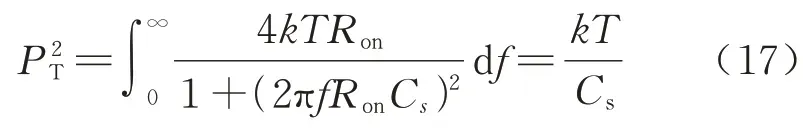
当采样开关在相应采样时钟作用下周期性进行采样时，KT 噪声被保存在采样电容上.KT 噪声的模型如图7 所示.

图7 KT 噪声建模Fig.7 KT noise modeling

3.2 比较器建模

比较器中输入噪声对SAR ADC 精度影响很大，是逐次逼近型ADC 结构中重要的噪声源.由于热噪声在频谱上均匀分布，所以比较器噪声与KT 噪声相似，都用随机信号建模.如图8 所示是对比较器噪声建模，其中Vrms为输入噪声的均方根电压值，其值根据实际电路中仿真获得.

图8 比较器噪声建模Fig.8 Comparator noise modeling

3.3 寄生电容建模

由于寄生电容的影响，模数转换器的性能会进一步下降［11-12］，图9 所示为带有寄生电容的单端电容阵列图，寄生电容用虚线框出.其中Cpl0～Cpl13和Cph1～Cph8分别为低段电容阵列和高段电容阵列中电容下极板的寄生电容，Cpl为低段阵列中所有电容上极板的寄生电容，Cph为高段阵列中所有电容上极板的寄生电容，Cpb为桥接电容Cb的寄生电容.

图9 带有寄生电容的电容阵列示意图Fig.9 Schematic diagram of capacitor array with parasitic capacitance

在ADC 工作过程中，由于电容下极板接固定电位，所以下极板的寄生电容对电荷的重分配没有影响，线性度不发生变化［13］，如果仅考虑Cph的影响，根据式（12），式（13）和式（14），可以看出Cph对Eq2和Eq3之间不产生影响，所以Cph不影响高段阵列和低段阵列之间的线性特性，对有效位数产生的影响十分微弱，而低段阵列的寄生电容Cpl和桥接电容的寄生电容Cpb对式（14）的Eq3产生影响，引起输出的增益误差，导致一定的非线性，从而影响ADC 精度，降低ADC 的有效位数.

基于以上分析，本文对SAR ADC 进行系统级建模并对寄生电容的影响进行仿真验证.在充分考虑系统级建模与实际偏差的基础上，假设Cph的值为最高有效位总电容CMSB的10%，Cpl为CLSB的10%，Cpb为Cb的10%.

4 系统仿真验证与对比分析

为了验证校准算法性能，假设所有电容均带有2%的随机失配误差，同时考虑上述非理想因素的影响，对SAR ADC 结构进行系统级建模，图10、图11 为反映校准算法收敛情况的各项性能指标的仿真结果图.图10 所示为式（3）中迭代误差Eerror的收敛过程，当迭代次数达到25 000 次时，Eerror可收敛到±1 LSB 以内.图11 所示为有效位数与迭代次数关系图，随着迭代次数增加，有效位数逐渐增加并最终趋于稳定，当迭代次数达到35 000 次时性能较优，有效位数ENOB 可达到13.75 bit.

图10 误差收敛过程Fig.10 Error convergence process

图11 有效位数与迭代次数关系图Fig.11 Relationship curve between ENOB and the number of iterations

图12 为反映SAR ADC 校准算法的性能参数的仿真图.图12（a）中，校准前SFDR 为60.0 dB，ENOB为9.28 bit，图12（b）中，校准后SFDR 为106.3 dB，ENOB 为13.75 bit.校准前后的结果对比表明，本文提出的校准方法应用于SAR ADC 能够获得很好的性能提升.

图12 校准前后算法输出信号FFT 结果Fig.12 Performance parameters of calibration algorithm

为了更好地说明本文提出的校准方法的可行性，进行100 次仿真验证，得出校准前后有效位数与其概率的分布，如图13 所示.图13（a）中校准前有效位数集中分布在9.5～10.5 bit 之间，图13（b）中校准后有效位数均在13.7 bit 以上.

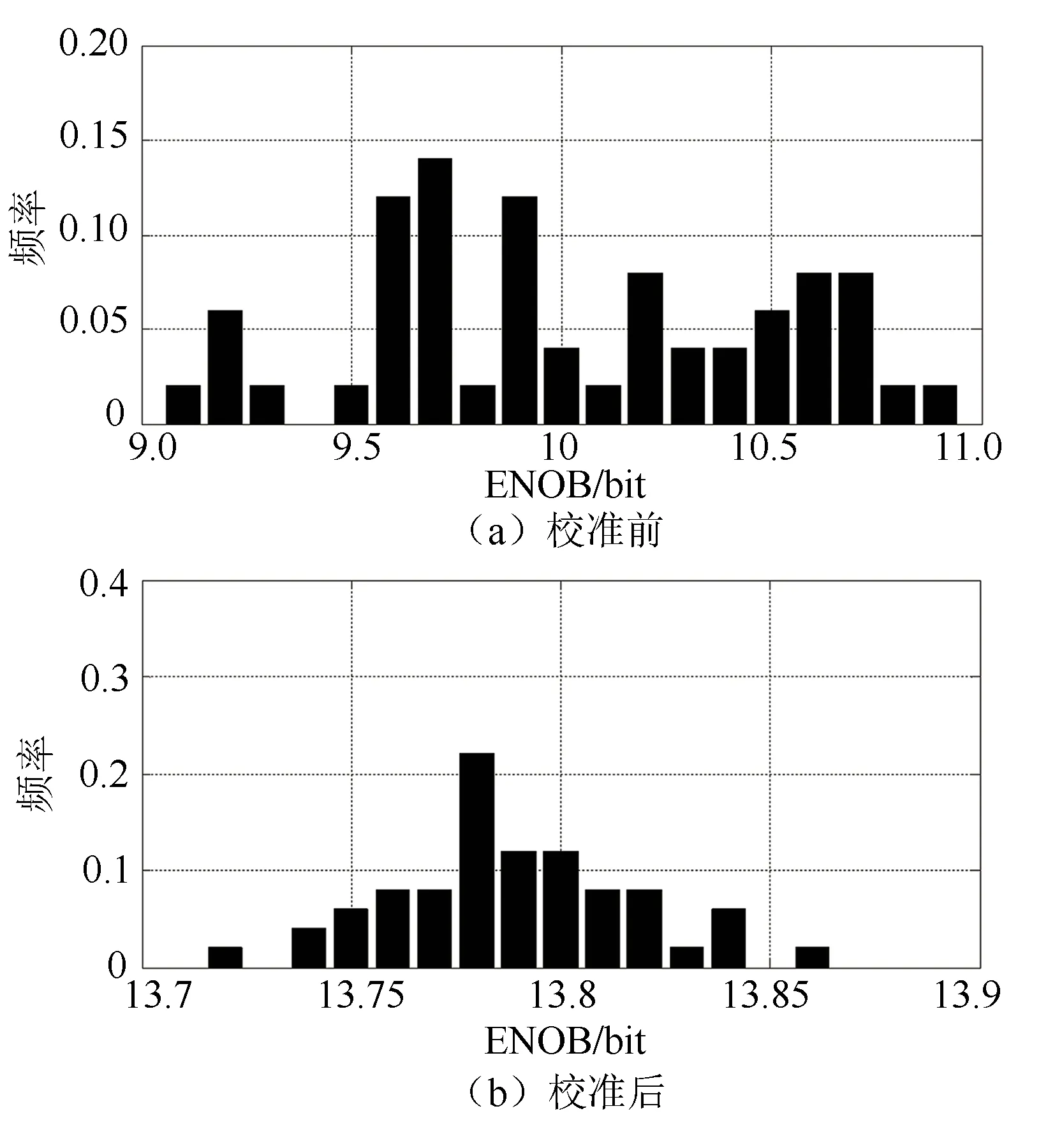
图13 仿真100 次有效位数概率分布图Fig.13 Probability distribution of ENOB obtained in 100 simulations

表2为本文与其他文献中SAR ADC 性能参数的对比结果.文献［14］采用数字自校准的的方式进行12 bit SAR ADC 的系统级建模仿真，仿真结果表明，校准前SAR ADC 的有效位数是9.983 1 bit，校准后为11.258 8 bit，有效位数提高了1.275 7 bit.文献［15］提出结合DEM 技术的基于LMS 算法的校准方法对13 bit SAR ADC 进行系统级建模仿真，仿真结果表明，校准前SAR ADC 的有效位数是7.95 bit，校准后为12.0 bit，有效位数提高了4.05 bit.采用本文的校准方法对14 bit SAR ADC 进行系统级建模仿真，仿真结果表明，校准前SAR ADC 的有效位数是9.28 bit，校准后为13.75 bit，有效位数提高了4.47 bit.与文献［14］和［15］相比，本设计采用的校准算法在SAR ADC 的性能上有更明显的提升.

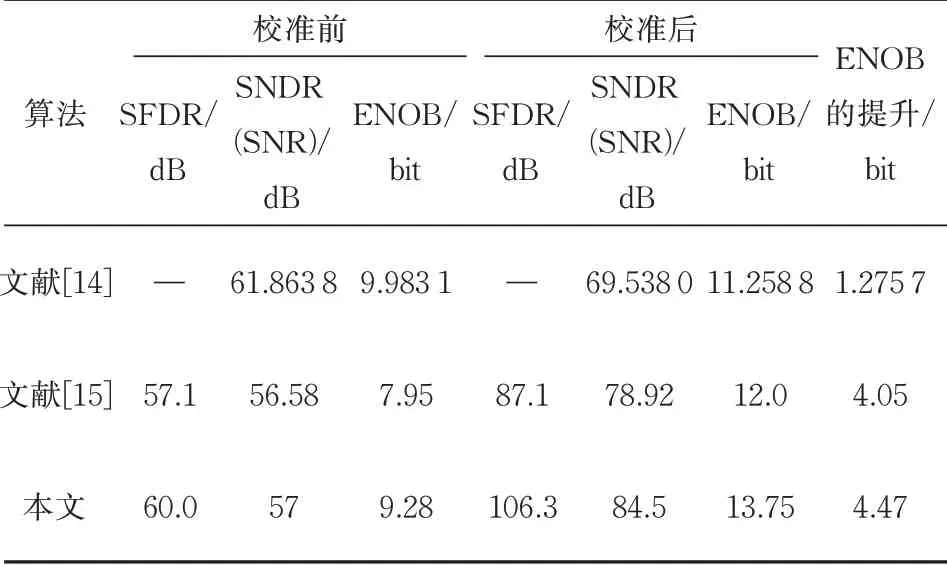
表2 本文与其他文献ADC 性能参数对比Tab.2 Comparisons of ADC performance parameters between this paper and other literatures

5 结论

1）由于SAR ADC 精度受电容失配、寄生效应等非理想因素的影响，采用整数权重非二进制结构的分段电容阵列结合LMS 算法，并且基于扰动信号注入的数字校准算法来提高SAR ADC 的精度.

2）仿真结果显示，该校准方法将SFDR 从60.0 dB提升到106.3 dB，将ENOB 从9.28 bit 提升到13.75 bit.为了更好地说明本文提出的校准方法的可行性，进行了100 次仿真，仿真结果验证了校准算法的正确性和有效性.