考虑接力器特性的导叶关闭规律

徐敏杰，陈胜，杨森，张健，王晶

(河海大学水利水电学院，江苏 南京 210098)

水电站在其运行周期中不可避免地会出现机组突甩负荷、导叶紧急关闭的工况，此时输水系统压力陡增，机组转速升高，威胁电站运行安全.获得合理的导叶关闭规律是平衡机组转速上升与水锤压力上升的必要措施[1-3]，导叶关闭速度越快，输水系统水锤压力越大，机组转速上升率越小，反之亦然.关于导叶关闭规律的优化，众多学者进行了大量的理论及实际研究.李敏等[4]研究了“先快后慢”的折线关闭规律适用的机组类型；王煜等[5]从过渡过程机组初始参数出发，提出了一种由初始参数决定的非固定模式导叶关闭规律；张健等[6-7]针对可逆机组提出了具有延时段的三段折线关闭规律及引入转速信号的导叶关闭规律；CHEN等[8]提出了一种两段折线关闭规律优化方法，有效限制了蜗壳压力与转速上升；周天驰等[9]应用模拟退火算法，以蜗壳压力、机组转速上升率和尾水管压力这3项指标的评价函数为基础，获得了全局较优的导叶关闭规律；ZHANG等[10]引入非支配排序遗传算法，针对高水头抽蓄电站水泵工况提出了两段折线及三段延时折线关闭规律，有效限制了水锤压力与转速上升；储善鹏等[11]针对抽蓄电站相继甩工况，提出了一种求解最优关闭规律的方法；张美琴等[12]提出了高水头可逆机组优选合适导叶关闭规律的若干建议；樊红刚等[13]建立了一种多工况优化导叶关闭规律的非线性评价函数，保证各工况均能满足控制要求.但在实际导叶关闭过程中，由于导流设备惯性等因素的存在，导叶关闭初始时刻存在迟滞过程.而在导叶关闭接近末期时，为了防止活塞撞击接力器油缸，需要设置缓冲关闭过程.对此，杨建东[14]认为在过渡过程仿真计算中导叶关闭规律应根据导叶的实际关闭情况模拟，不宜使用概化的直线关闭规律代替.

数值仿真中导叶关闭规律常采用概化的直线关闭规律而忽略了迟滞与缓冲过程.为探究考虑迟滞与缓冲过程的导叶关闭规律对蜗壳压力、尾水管压力及机组转速极值与时程的具体影响，文中基于特征线法，针对国内某引水式水电站，建立水力过渡过程数值仿真模型，并在导叶关闭过程中考虑迟滞与缓冲过程，对比概化直线关闭结果，分析二者蜗壳压力、尾水管压力及机组转速极值与时程的差异.

1 数学模型原理

1.1 水锤基本方程

将有压管道水流运动的基本方程进行线性组合，并沿特征线积分，即可得到求解时刻方程[15-16]为

C+:Hpi=Cp-BQpi,

(1)

C-:Hpi=CM+BQpi,

(2)

其中，Cp，CM由上一时刻水头和流量求出，即

Cp=Hi-1+BQi-1-RQi-1|Qi-1|,

(3)

CM=Hi+1-BQi+1+RQi+1|Qi+1|,

(4)

式中：Hpi为求解时刻测压管水头；B=a/gA，其中，a为水锤波速，g为重力加速度，A为管道面积；R=fΔx/(2gdA2)，其中，f为摩擦系数，Δx为管道分段长度，d为管道直径；Qpi为求解时刻流量；Hi-1，Qi-1为上一时刻i-1位置水头和流量；Hi+1，Qi+1为上一时刻i+1位置水头和流量.

1.2 考虑接力器特性的导叶关闭模型

在导叶一段直线关闭规律中，考虑接力器特性与未考虑接力器特性的关闭规律的对比如图1所示，图中Tz为导叶完全关闭时间；Ts为导叶有效关闭时间；Tc为迟滞时间；Tk为缓冲时间；点B，C为考虑接力器特性与不考虑接力器特性关闭规律的交点；τ为导叶相对开度.

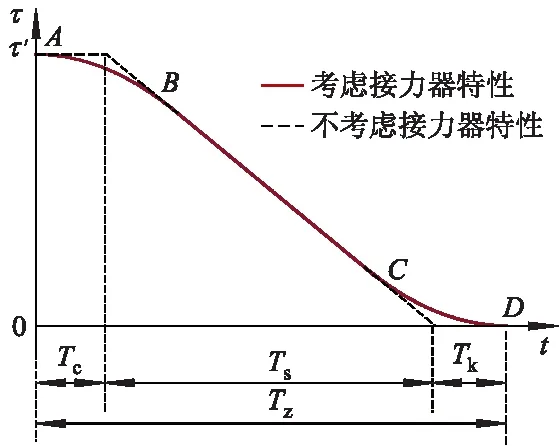
图1 考虑接力器特性与不考虑接力器特性关闭规律

为方便表示，Tc，Tk可由Tz表示，即

Tc=kcTz,

(5)

Tk=kkTz.

(6)

由于考虑接力器特性的关闭规律各项参数未知，为了求得导叶关闭规律的解析式，进行如下假设：

1)迟滞与缓冲过程导叶相对开度近似符合二次函数关系；

2)点B，C处连接光滑.

Tc与Tk大小可根据真机甩负荷试验数据反演得到，在缺乏资料时，kc与kk可近似取kc+kk=0.3[17]，点C开度取空载开度.

若已知导叶有效关闭时间Ts、迟滞时间Tc、缓冲时间Tk及点A坐标(0，τ′)，可以得到导叶关闭BC段延长线过点(Tc，τ′)及(Ts+Tc，0)，以此得到BC段直线解析式

(7)

设点B坐标为(Bx，By)，由假设1)，2)可得

(8)

(9)

由式(7)，(8)，(9)可得点B坐标(2Tc，τ′(1-Tc/Ts))及导叶关闭AB段解析式

(10)

同理，可得CD段关闭规律的解析式，进而获得整个导叶关闭规律的解析式

(11)

2 工程实例与分析

国内某水电枢纽为二等大(2)型工程，电站共有2个水力单元，引水系统采用四机四洞布置形式，尾水系统采用四机两洞的布置形式.电站总装机容量990.0 MW，设置4台单机容量为247.5 MW的混流式水轮机组，机组最大水头92.00 m，额定水头81.00 m，最小水头75.20 m，机组额定出力252.6 MW，额定流量340.84 m3/s，额定转速115.4 r/min.上下水库特征水位表如表1所示，表中hup为上库水位，hlow为下库水位.电站平面示意图如图2所示.

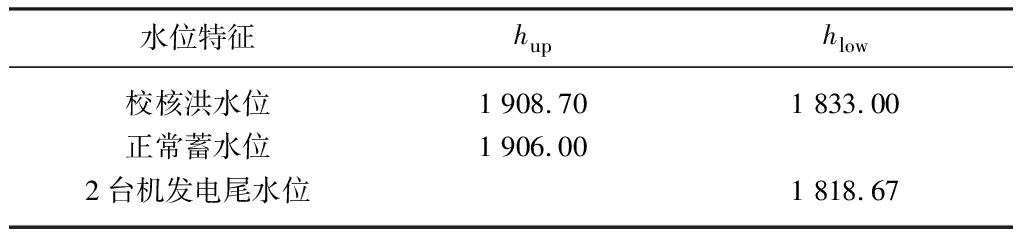
表1 电站上下水库特征水位

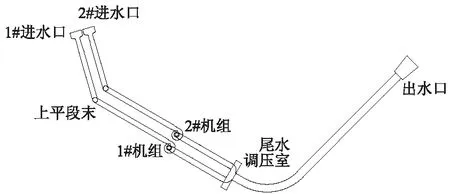
图2 某引水式电站引水发电系统布置

基于1.1及1.2节相关原理，建立该电站的水力过渡过程数值仿真模型，并选取2个设计工况作为蜗壳最大压力、机组转速最大上升率以及尾水管最小压力的控制工况，具体工况见表2.

表2 代表性计算工况

2.1 实测工况及关闭规律确定

为了确定kc和kk值，这里使用真机甩100%负荷的实测数据.实测数据工况为上游水位1 903.56 m，下游水位1 819.90 m，机组甩100%负荷，调保参数时程如图3所示.图中Ht和Hw分别为蜗壳压力及尾水管压力；f为机组频率；τ为导叶相对开度.

图3 真机甩全部负荷试验各调保参数时程

由于实测压力数据测点位置的不确定性，这里需要对数据进行适当调整换算.由图3可得真机甩负荷导叶关闭规律.真机导叶关闭规律可近似视为由迟滞关闭、先快后慢的折线关闭、缓冲关闭组成.其中，迟滞关闭时间短，在图中几乎没有体现；先快后慢的折线关闭采用第1段-1/9 s-1斜率、第2段-1/20 s-1斜率、折点开度0.5的关闭规律；缓冲关闭近似直线关闭，但仍存在一定波动；未考虑接力器特性的导叶关闭规律主要模拟真机关闭规律中的折线关闭规律，故其关闭速率与折点位置与真机第2部分关闭规律一致；考虑接力器特性的关闭规律由迟滞过程、两段折线关闭、缓冲过程3部分组成.注意到文中模型以二次函数近似缓冲过程，与真机缓冲过程存在差异.差异可能会对缓冲过程内蜗壳压力Ht及尾水管压力Hw时程产生影响.为了尽可能减小这种差异对蜗壳压力、尾水压力等调保参数极值与时程的影响，这里尽量保证与真机导叶完全关闭时间基本一致.基于真机关闭规律，考虑接力器特性的导叶关闭规律，迟滞关闭过程由第1段折线控制，kc1为0.01，kk1为0；缓冲过程由第2段折线控制，kc2为0，kk2为0.40.这3种不同关闭规律见图4，各关闭规律计算结果见图5—7，极值对比见表3.表中，Ip为水压上升率；Dp为水压下降率;Inmax为转速上升率最大值.为方便理解与表述，表3及之后蜗壳压力及尾水管压力单位由MPa换算为m表示.

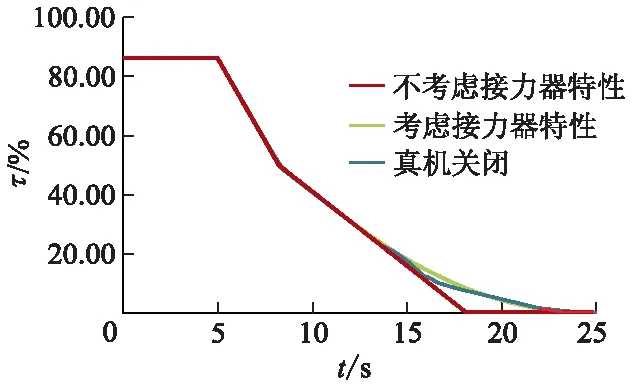
图4 3种不同类型的导叶关闭规律

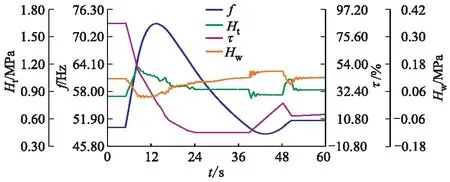
图5 真机关闭规律调保参数时程

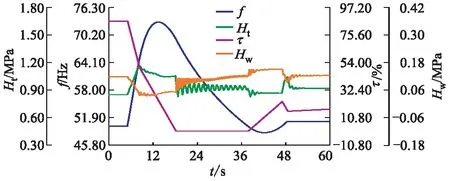
图6 未考虑接力器特性调保参数时程

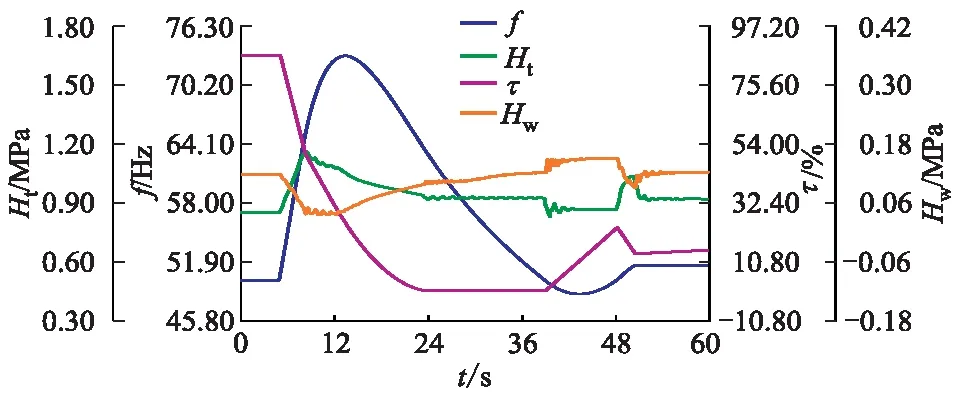
图7 考虑接力器特性调保参数时程

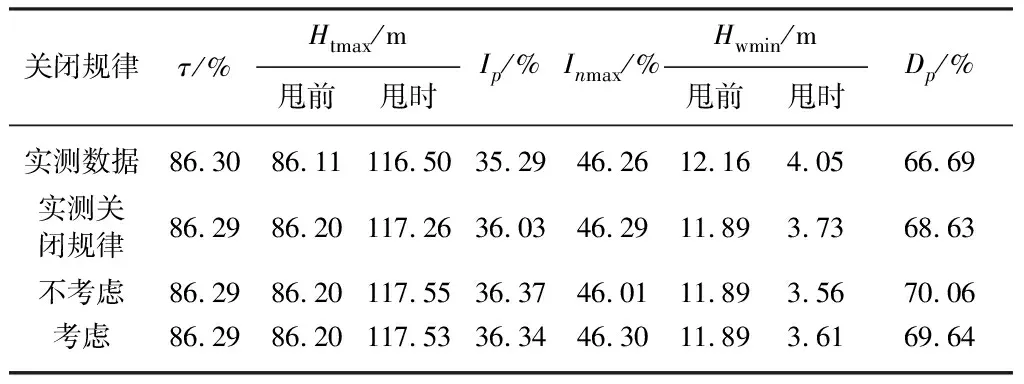
表3 实测数据与数值模拟结果对比

由表3及图3,5,6,7可知，基于该电站输水系统建立的水力过渡过程计算模型可以较为精确地预测其蜗壳、尾水管压力以及机组转速上升率的极值及时程.使用考虑接力器特性的关闭规律可使机组转速极值接近实测数据与实测关闭规律仿真计算结果，而对蜗壳压力及尾水管压力极值影响很小；在模拟导叶关闭末期蜗壳压力及尾水管压力时程时，使用考虑接力器特性的关闭规律较未考虑的关闭规律更接近实测数据与实测关闭计算时程.为了进一步探明迟滞与缓冲过程在不同工况下对调保参数的影响，采用控制工况进行计算.

2.2 控制工况计算结果对比

采用考虑接力器特性与未考虑接力器特性关闭规律，分别对T1,T2工况进行过渡过程计算，其蜗壳压力、尾水管压力及机组转速时程见图8—11，各工况调保参数极值统计见表4.

表4 控制工况使用考虑接力器特性与未考虑接力器特性的关闭规律极值计算结果对比

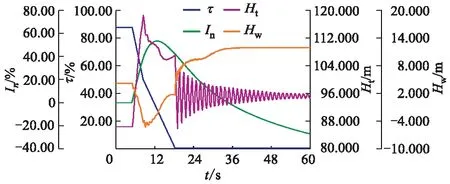
图8 T1工况未考虑接力器特性的调保参数时程

图9 T1工况考虑接力器特性的调保参数时程

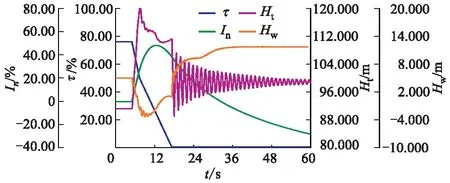
图10 T2工况未考虑接力器特性的调保参数时程

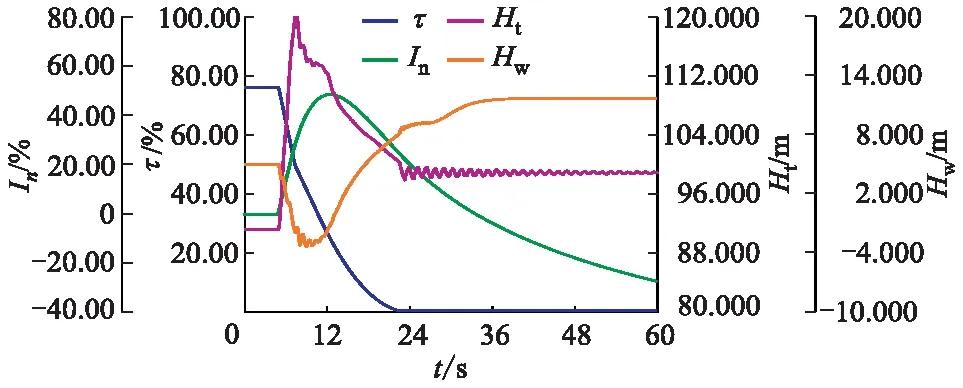
图11 T2工况考虑接力器特性的调保参数时程

由图8—11可知，在工况T1与T2中，考虑接力器特性与未考虑的关闭规律调保参数时程总体趋势一致，但在导叶关闭末期考虑接力器特性与未考虑接力器特性的蜗壳压力时程振荡程度及尾水管压力上升值存在显著差异：在T1工况导叶关闭末期，未考虑的蜗壳压力最大振幅为21.190 m，尾水管压力上升4.810 m；考虑接力器特性的蜗壳压力最大振幅为2.240 m，尾水管压力上升0.580 m；T2工况导叶关闭末期，未考虑接力器特性的蜗壳压力最大振幅为22.340 m，尾水管压力上升5.050 m；考虑接力器特性的蜗壳压力最大振幅为2.240 m，尾水管压力上升0.610 m.在T1工况导叶关闭末期，不考虑接力器特性的机组过流量降低0.640 m3/s，而考虑接力器特性的机组过流量降低0.062 m3/s.考虑接力器特性的关闭规律在导叶关闭期流量变化小，计算结果稳定.

由表4可知，在T1工况及T2工况，考虑接力器特性的关闭规律较未考虑的关闭规律，其机组转速上升率极值增大0.34%及0.29%，转速上升率极值增大是因为迟滞过程增加了从机组甩负荷到转速极值出现的时间，水流动力矩对水轮机作用的时间更长；蜗壳压力及尾水管压力极值影响很小：尾水管压力极值增大0.04%及0.12%，蜗壳压力极值则增大0.02%及减小0.01%.缓冲过程发生的时间较晚，此时各调保参数已经出现极值，故缓冲过程对调保参数极值没有影响.为了进一步分析迟滞过程对蜗壳压力及尾水管压力极值影响，对迟滞时间进行敏感性分析.

2.3 迟滞时间敏感性分析

文中在不同迟滞时间下，考虑接力器特性的导叶关闭规律对调保参数极值的影响.

不同kc1下导叶关闭规律见图12，其中导叶关闭规律区域Ⅰ即为迟滞时间，kc1值越大，迟滞时间越长；T1工况蜗壳压力时程见图13.蜗壳压力、尾水管压力及机组转速极值变化见表5.由图13可知，迟滞过程仅对7 s前蜗壳压力时程有一定影响，7 s后导叶关闭规律基本相同且蜗壳压力时程也基本相同，故迟滞过程仅影响过程内蜗壳压力时程，且影响不大.由表5可知，随着kc1逐渐增大，迟滞时间逐渐变长，机组转速极值呈直线正相关；而蜗壳压力及尾水管压力极值在不同工况下随迟滞时间变化的规律不同，T1工况蜗壳压力极值先增后减，尾水管压力极值先减后增；T2工况蜗壳压力极值随kc1增大而减小，尾水管压力极值则先增后减再增，迟滞时间的延长对蜗壳压力及尾水管压力并无明显改善作用.迟滞过程可视为延缓导叶关闭速度，一般来说蜗壳压力及尾水管压力将有所改善.迟滞时间的延长影响了机组的转速上升率，增强了机组的“截流”效果，不一定会改善蜗壳压力及尾水管压力.

图12 T1工况不同kc1下导叶关闭规律

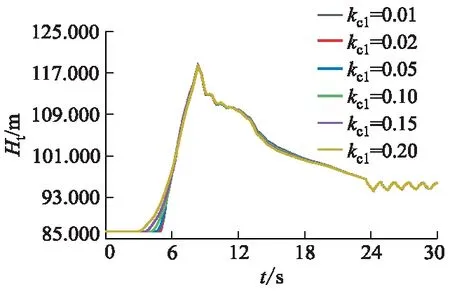
图13 T1工况不同kc1下蜗壳压力时程

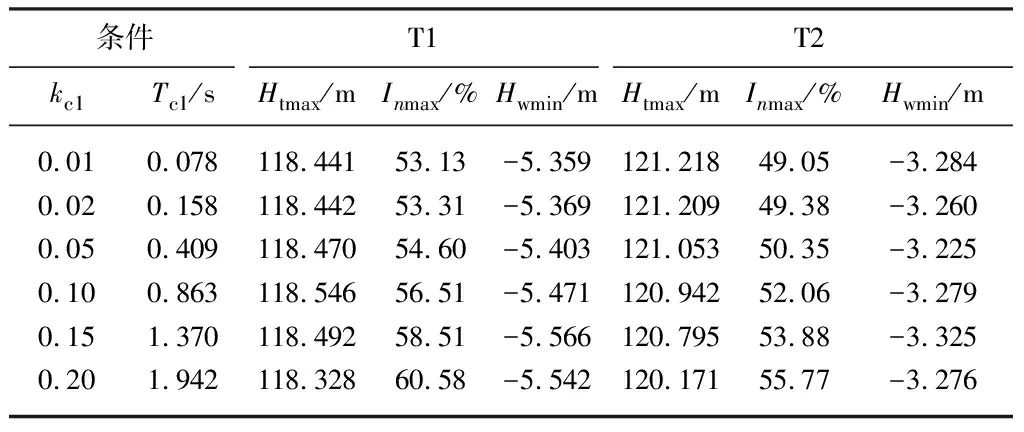
表5 控制工况kc1值对调保参数极值影响分析结果

3 结 论

1)迟滞与缓冲过程采用二次函数近似，较未考虑迟滞缓冲过程模型，考虑迟滞缓冲模型可以更为精确地预测蜗壳压力、尾水管压力、机组转速的极值及时程，模型建立正确.

2)迟滞过程对机组转速最大上升率呈直线正相关，而对蜗壳压力及尾水管压力极值则影响较小.缓冲过程则由于其发生时间一般迟于各调保参数极值发生时间，故其对于调保参数极值几乎没有影响.

3)使用考虑接力器特性的导叶关闭规律可以降低导叶关闭末期机组过流量变化，有效改善蜗壳压力及尾水管压力时程振荡的情况.

4)延长迟滞时间增强了机组的“截流”效果，不一定会改善蜗壳压力及尾水管压力.