一种面向即插即用车载GNSS/INS/ODO系统的时空在线标定方法
岑益挺,赖际舟,吕 品,白师宇,李金鑫
(1. 南京航空航天大学自动化学院,南京 211106;2. 中国兵器装备集团兵器装备研究所,北京 102202)
0 引言
全球卫星导航系统(Global Navigation Satellite System,GNSS)与惯性导航系统(Inertial Navigation System,INS)在陆地车辆组合导航中可以提供位置、速度和姿态等完备导航信息,在民用和军用领域得到了广泛的研究与应用。在组合导航系统中,GNSS通过接收卫星信号解算得到准确的三维位置和速度信息,但是由于信号容易受隧道峡谷、高楼树木等遮挡以及电磁干扰,导致GNSS无法有效地进行定位和测速;INS凭借全自主的优势,能够在短时间内提供精确的导航信息,但是其误差会随时间快速累积,需要GNSS在车辆运动过程中进行抑制。而当GNSS不可用时,需要再引入辅助信息,修正INS单独导航时的误差,如零速修正、地图匹配、激光雷达、相机、轮速里程计等。
轮速里程计(Odometer,ODO)作为另一个自主且经济、方便搭载的车载传感器,可以提供车辆的前向速度,与车辆非完整约束(Non-Holonomic Constraints,NHCs)结合,可以有效提高GNSS失效时INS的导航精度,而精度提升的关键在于惯性测量单元(Inertial Measurement Unit,IMU)与ODO之间参数的准确标定。通常两者之间的杆臂可以通过手动测量的方式进行补偿,但操作较为繁琐且测量精度较低,另外安装偏差角难以测量,因此研究在GNSS有效时利用其辅助IMU/ODO参数在线估计,对提升GNSS失效时INS/ODO组合导航精度具有积极意义。文献[11]和文献[12]分别通过卡尔曼滤波与非线性优化实现了GNSS辅助IMU/ODO的在线标定,过程中考虑了GNSS天线与IMU之间的杆臂,但是均未考虑GNSS时延与ODO时延的影响。在系统集成化较高的车载导航应用中,通常采用硬件同步的方式统一各传感器的时钟,但是对于即插即用的系统而言,每当传感器需要更新或者改变时,硬件同步会带来巨大的成本。目前,许多研究者已经对传感器时延以及软件时间同步方法开展了不少研究。文献[13]中指出,GNSS接收机的信号处理过程给GNSS输出带来的延时达到百毫秒级别,对GNSS实时应用带来的影响不可忽视。文献[14]研究了GNSS/INS系统的时延估计与补偿算法。但是针对GNSS/INS/ODO系统,目前尚未有文献同时考虑GNSS与ODO的时延,且两种时延对GNSS辅助IMU/ODO参数在线标定带来的影响也尚未有文献进行研究。
针对上述问题,本文提出了一种面向即插即用车载GNSS/INS/ODO系统的时空在线标定方法。该方法分析了GNSS时延与ODO时延在车辆运动过程中对IMU/ODO在线标定的影响,在传统GNSS辅助IMU/ODO参数估计模型的基础上,增广了GNSS与ODO的时延误差,并且构建了完整的GNSS与ODO观测模型,采用卡尔曼滤波器对GNSS时延、ODO时延以及IMU与ODO之间的参数进行估计。实际测试结果表明,该方法可以有效提高IMU/ODO在线标定的精度。
1 坐标系定义
本文采用的坐标系定义如图1所示。
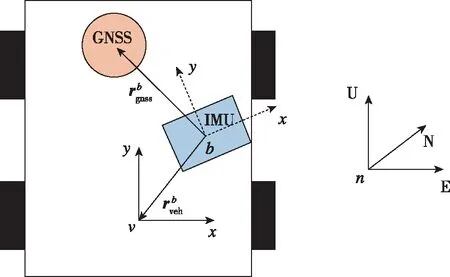
图1 坐标系定义
1)车体坐标系(系):以车体后轴中心作为坐标原点,轴沿车体向右,轴沿车体向前,轴与轴、轴形成右手坐标系;
2)IMU坐标系(系):以IMU的中心作为坐标原点,与系同为右前上坐标系;
3)导航坐标系(系):为东北天(ENU)坐标系。
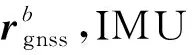
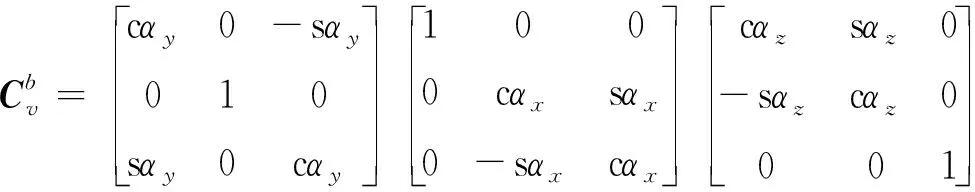
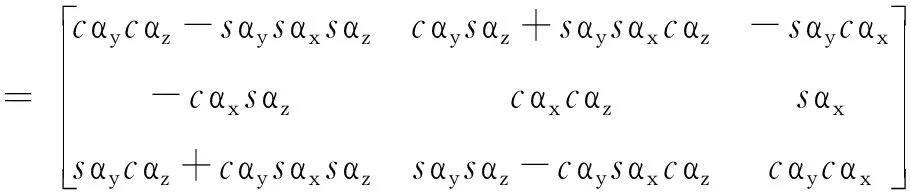
(1)
其中,三角函数sin和cos分别用s和c表示。
由于安装偏差角通常为小角度,则式(1)可以近似为
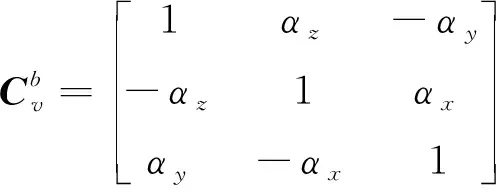
(2)
则系下速度与系下速度之间的关系为
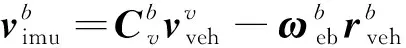
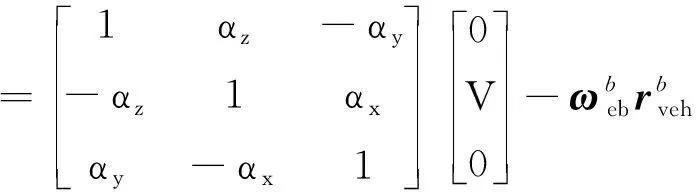
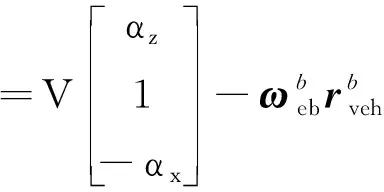
(3)
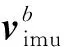
根据式(3)可知,系下的速度在系下的分量与安装偏差角无关,在标定时可以不作考虑。
2 改进GNSS辅助IMU/ODO参数估计滤波器设计
2.1 GNSS时延对IMU/ODO标定的影响分析
对于GNSS/INS组合导航系统,由于GNSS接收机与IMU的采样时间不一致,且信号处理时间也不一致,导致两者存在时延且时延相对稳定。假设GNSS位置观测的时延为一个固定值,则时刻GNSS位置观测的实际值可以建模为
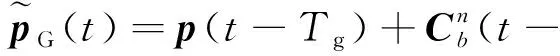
(4)
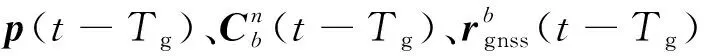
由于时刻GNSS的实际位置观测为-时刻的值,因此在用INS预测GNSS位置时,需要预测-时刻的值
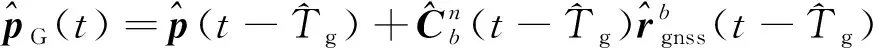
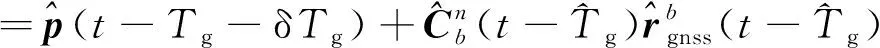
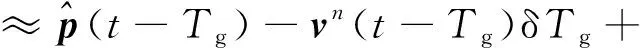
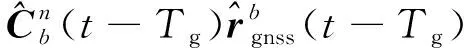
≈(-)+δ(-)-
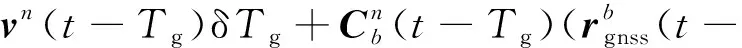
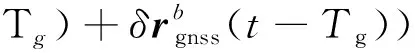
=(-)+δ(-)-
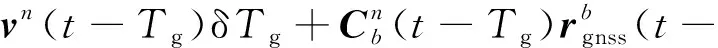
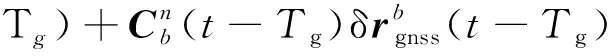
(5)
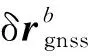
将GNSS位置的预测量与观测量作差,得到位置量测方程为
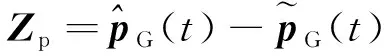
=δ(-)-(-)δ+
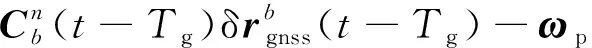
(6)
根据文献[15]对IMU/ODO参数标定的可观测性分析可知,轮速里程计标度因数误差以及IMU与ODO之间安装偏差角的估计需要车辆的加减速机动激励,而IMU与ODO之间的杆臂估计需要至少绕2个轴向的角速度机动激励。而在上述机动下,GNSS时延对IMU/ODO标定的影响具体如下:
1)根据式(6)可知,GNSS时延将与车辆速度耦合引起GNSS位置观测误差,从而降低滤波器对INS位置误差的估计精度;
2)在IMU/ODO标定所需的加减速或角速度机动下,速度矢量的大小或方向发生变化,使得GNSS时延带来的INS位置误差同步改变,从而引起INS速度误差,影响IMU/ODO的参数标定。
2.2 ODO时延对IMU/ODO标定的影响分析
同样假设ODO与IMU之间的时延为一个固定值,则时刻ODO速度观测的实际值可以建模为
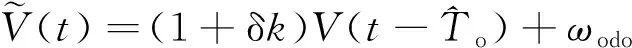
=(1+δ)(--δ)+
=(1+δ)((-)-(-
)δ)+
≈(1+δ)(-)-(-
)δ+
(7)
其中,δ为轮速里程计的标度因数误差;δ为ODO与IMU之间残余待估计的时延值;(-)为-时刻车辆的前向加速度;为速度观测噪声。
根据式(7)可知,ODO时延与车辆前向加速度耦合引起轮速里程计的速度观测误差,从而直接影响其标度因数误差的估计。
2.3 基于GNSS与ODO时延估计的IMU/ODO滤波模型
为降低GNSS与ODO时延对IMU与ODO之间参数估计的影响,将GNSS与ODO时延增广到状态量中。基于GNSS与ODO时延估计的IMU/ODO参数估计滤波结构如图2所示。
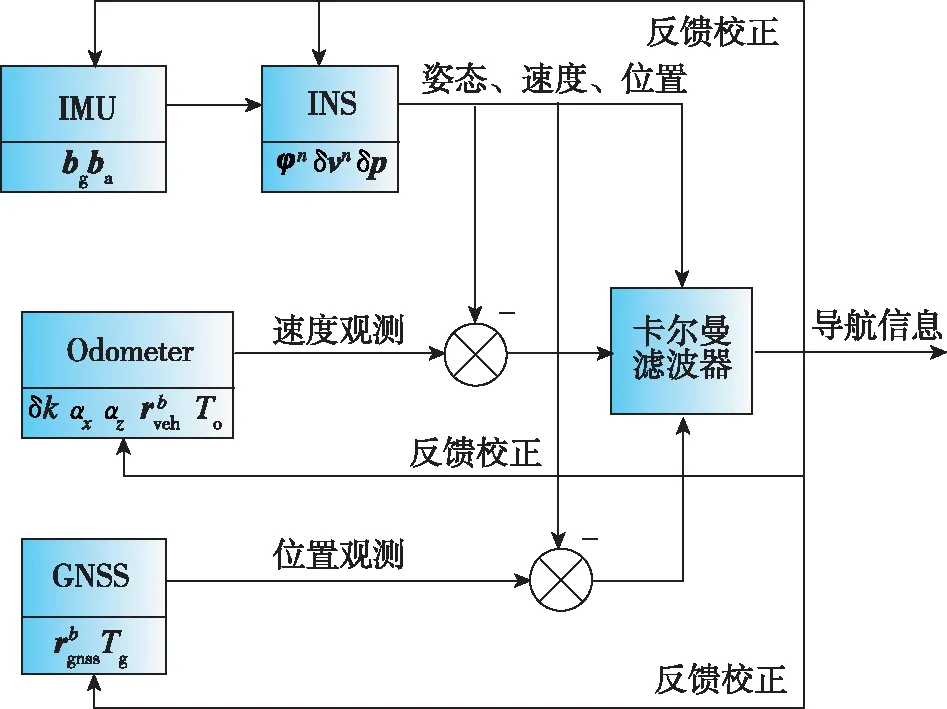
图2 基于GNSS与ODO时延估计的IMU/ODO参数估计滤波结构
此时,状态方程为
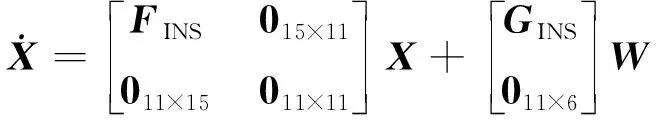
(8)
其中
=[(),(δ),(δ),(),(),
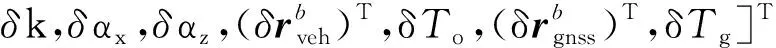
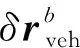
式(8)中,和为INS的状态转移矩阵和系统噪声矩阵,具体形式可参见文献[16];为INS的系统噪声,即陀螺和加速度计的白噪声。
轮速里程计与非完整约束一起构成系下的三维速度观测
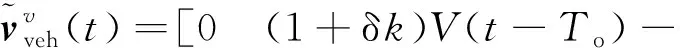
(9)
根据式(9)可以得到系下的速度观测
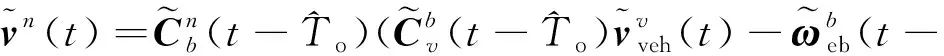
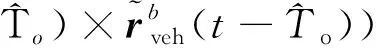
≈(-)+[(-)×](-)+
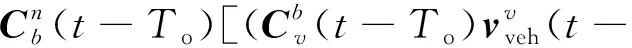
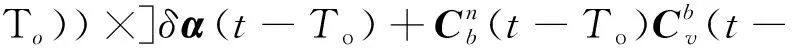
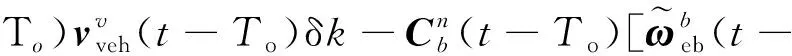
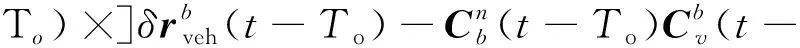
)(-)δ+
(10)
而根据INS得到的时刻的速度为
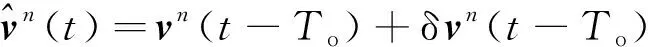
(11)
将式(10)与式(11)作差,得到速度量测方程为

=-[(-)×](-)+δ(-)-
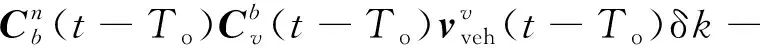
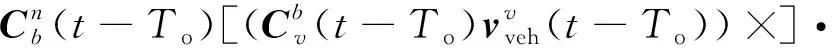
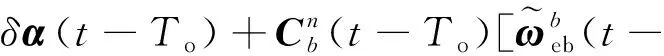
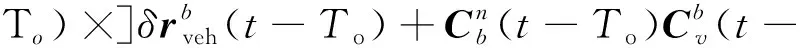
)(-)δ
=(-)-
(12)
其中,为速度量测矩阵。
根据式(6)可得位置量测方程为
=(-)-
(13)
其中,为位置量测矩阵。
3 试验验证
本文开展了实际试验,以验证所提出的算法。试验所用IMU的性能参数如表1所示,轮速里程计的测速精度为0.02m/s,GNSS位置精度为0.05m。IMU、轮速里程计以及GNSS天线的安装如图3所示,其中GNSS后天线与IMU之间杆臂的粗略测量值为[0.2,-1.15,0.5]m。试验轨迹如图4所示,试验总时长35min,其中试验过程前20min用于GNSS/INS/ODO系统的参数在线标定,后15min用于验证基于GNSS与ODO时延估计的IMU/ODO参数在线标定方法的准确性,后15min行驶路程约1380m。由于IMU与ODO之间参数的真值未知,本文采用如下两种方式间接验证:

图3 车辆试验平台
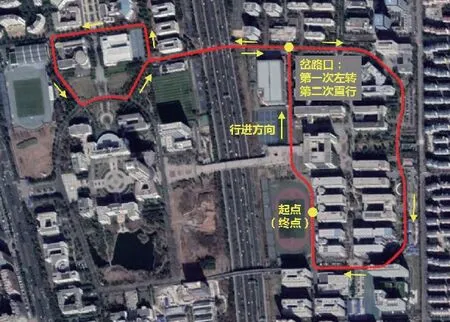
图4 试验轨迹

表1 IMU性能参数
1)方式1:后15min进行GNSS/INS组合导航,以IMU/ODO在线标定的结果作为已知量,检验车辆非完整约束的满足情况。
2)方式2:后15min以IMU/ODO在线标定的结果作为已知量,进行INS/ODO组合导航,以差分GNSS信息为位置基准,检验INS/ODO组合导航的定位精度。
前20min在线标定试验过程中,位置、速度、姿态如图5所示。
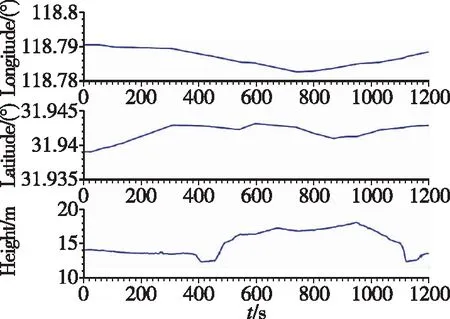
(a)
为了具体对比GNSS时延与ODO时延对IMU/ODO参数在线标定的影响,将不考虑GNSS时延与ODO时延(记为M1)、仅考虑GNSS时延(记为M2)以及本文同时考虑GNSS时延与ODO时延(记为M3)的参数标定方法进行对比,标定结果如表2所示,图6~图8所示为对应的标定曲线。图9所示为本文方法的GNSS时延与ODO时延估计曲线。图6~图8中,除δ之外,M2与M3的其余参数标定曲线几乎重合。
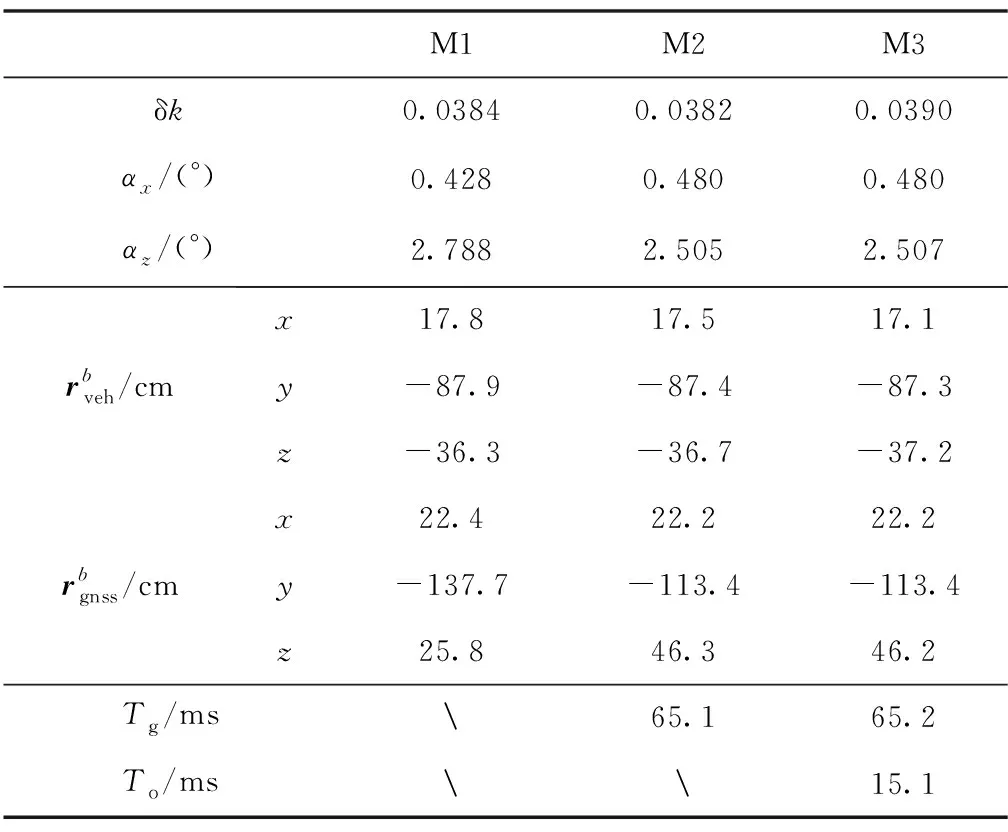
表2 参数标定结果对比
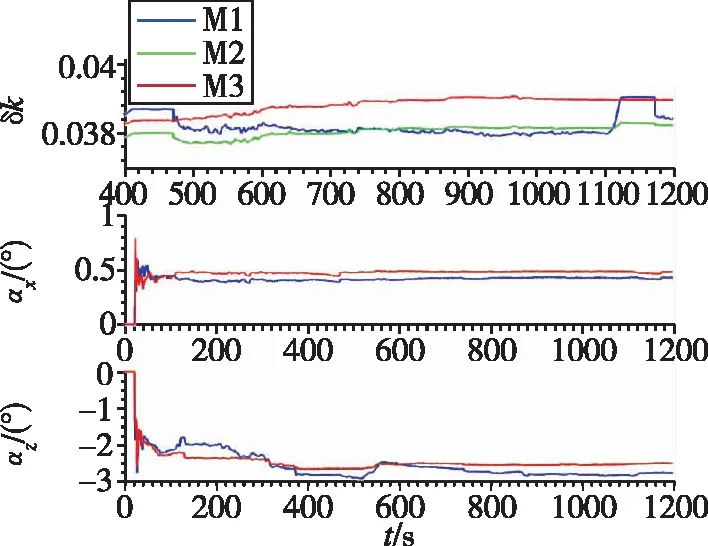
图6 ODO标度因数误差、IMU与ODO之间的安装偏差角估计对比
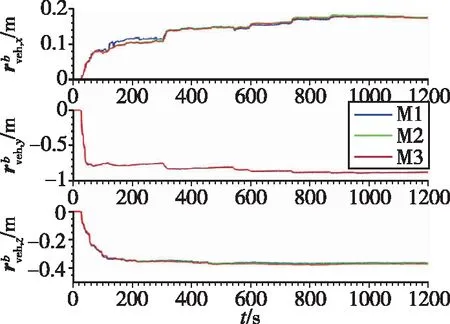
图7 IMU与ODO之间的杆臂估计对比
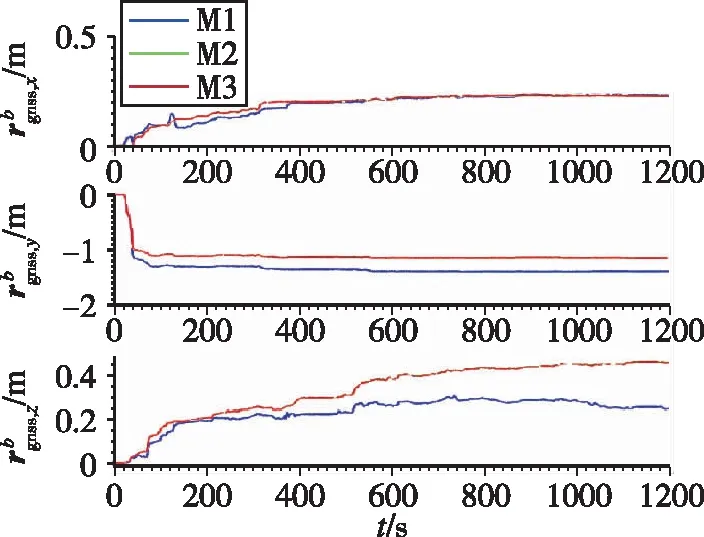
图8 GNSS天线与IMU之间的杆臂估计对比
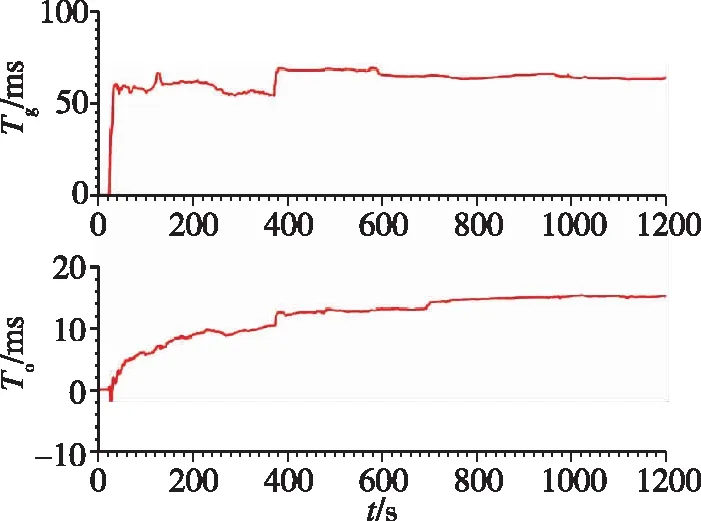
图9 GNSS时延与ODO时延估计
根据图6~图9以及表2数据可以看出:
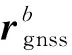
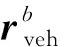
3)GNSS时延对IMU与ODO之间的标度因数误差δ以及安装偏差角、的标定影响较大。从图6可以看出,在470s、1120s车辆加减速时,δ出现明显的跳变,在130s时由于车辆的减速再加速,导致M1与M2对、的估计结果出现较大差异,这都是因为试验中加减速机动较为明显,GNSS时延引起的INS速度误差较大所致。
4)本文试验中使用的轮速里程计存在15ms左右的时延,其主要在470s、1120s等车辆加减速时引起轮速里程计标度因数误差估计的跳变,不过由于ODO时延量较小,因此跳变幅度较小。
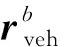
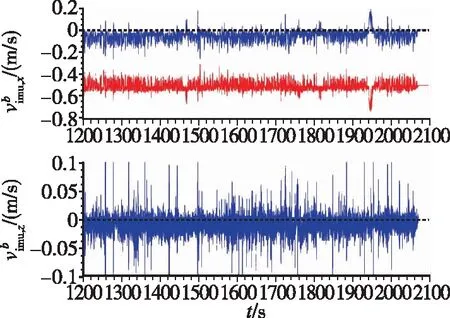
图10 b系下的速度
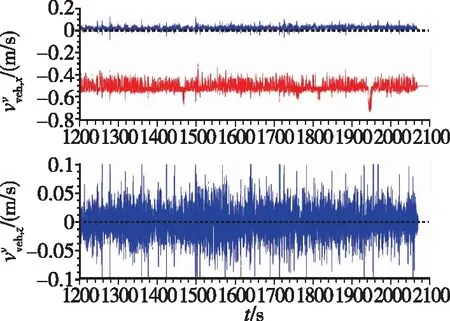
图11 经M1标定结果补偿后的v系下速度
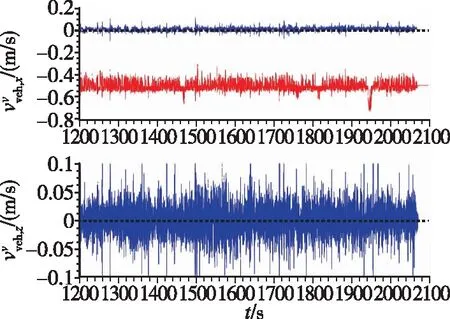
图12 经M3标定结果补偿后的v系下速度
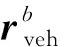
为了进一步体现使用本文方法对IMU/ODO标定补偿后INS/ODO组合导航系统在GNSS失效时的定位性能优势,开展了前文方式(2)所述的验证工作。图13所示为经过M1、M2与M3三种方法标定结果补偿后的INS/ODO组合导航系统水平位置误差与高度误差对比图,最大位置误差对比如表3所示。
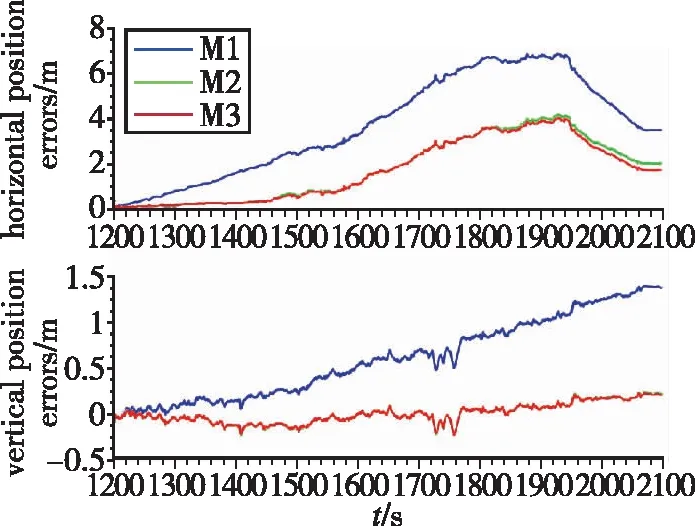
图13 INS/ODO组合导航系统水平位置误差与高度误差对比
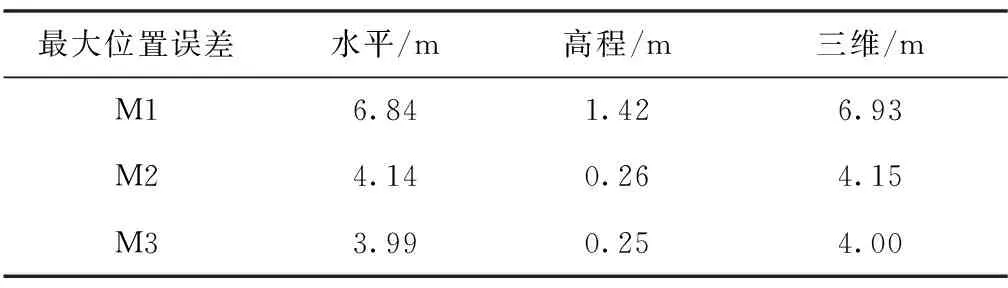
表3 INS/ODO组合导航系统最大位置误差对比
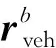
4 结论
本文提出了一种面向即插即用车载GNSS/INS/ODO系统的时空在线标定方法。该方法在传统GNSS辅助IMU/ODO参数估计模型的基础上,增广了GNSS与ODO的时延误差,分析了两种时延对IMU/ODO参数在线标定的影响,推导并构建了完整的GNSS与ODO观测模型,采用卡尔曼滤波器对GNSS时延、ODO时延以及IMU与ODO之间的参数进行估计。实际测试结果表明,该方法可以有效提高IMU/ODO在线标定的精度。

