基于高光谱特征的土壤含水量遥感反演方法综述
晏红波, 韦晚秋, 卢献健, 杨志高, 黎振宝
(1.桂林理工大学测绘地理信息学院,桂林 541004; 2.广西空间信息与测绘重点实验室,桂林 541004)
0 引言
了解不同时空尺度上的土壤含水量θ对于监测和模拟水文过程、植物生长、气候变化、土壤侵蚀、土地退化和荒漠化是十分重要的[1]。传统上,土壤含水量是直接用称重法估计的[2]。该方法虽然最准确,但需要大量的人力进行采样和测量,且样品本身也会遭到破坏,使得测量结果无法重现。其他需要采样取点测量的间接方法包括张量计、时域反射计、中子仪探针、电容传感器和伽马射线扫描仪等[3-6],这些方法存在时空异质性,不适合在不同时空尺度下表征土壤含水量。
随着遥感技术的广泛应用,微波、热红外和光学遥感估算土壤含水量的潜力也被大家所认可[7-8]。在微波遥感(5~1 000 mm)估算土壤含水量与波长后向散射系数有关,其在大范围的应用中效果明显,但是不足之处是它的空间分辨率较低,不适用于小尺度以及野外测量; 对于热红外遥感(3.5~14μm)监测反演土壤含水量,一般来说,当与能够提供植被指数的光学传感器协同使用时,其估算精度较高[9],但反演计算过程中涉及多种复杂的导数,反演解算过程较为繁琐,研究小范围的土壤含水量情况下不推荐使用该方法,更推荐在大面积情况下使用; 高光谱分辨率的光学遥感(400~2 500 nm),通常称为高光谱遥感(hyperspectral remote sensing, HRS),由于土壤含水量θ与土壤的高光谱反射率R之间的相关性较大,将其与地面、机载和高空传感系统结合使用,可以在不同时空尺度上估算出土壤含水量。因此,HRS被认为是解决上述估计土壤含水量θ存在空间分辨率低、适用范围小等问题上最有前途的遥感技术之一。
1 土壤含水量与光谱反射率关系
图1反映的是土壤反射率随波长的变化关系。从图1可看出不同波长所对应土壤的反射率不尽相同,在1 450 nm和1 900 nm波长附近土壤反射率较低,出现了明显的波谷,在1 300 nm和1 700 nm波长附近土壤反射率达到了一个较高值,出现了较为明显的波峰,因此可以根据这几个波长范围与土壤反射率之间的相互关系来估算出土壤含水量。作为HRS应用于估计土壤含水量的一个步骤,一些实验室研究使用近距离高光谱传感器(通常也称为漫反射光谱)来研究不同θ下R的变化[10]。一般来说,增加R会产生2个显著的影响: 一是整体R的非线性程度降低使得其对湿度较为敏感的波段的吸收增加; 二是非线性R随θ的增大而增大,其原因是土壤-水-空气界面的反射指数减小[11],从而降低了入射光的散射和由于水-空气界面上的附加反射而引起的散射光的深度传播[12],这种关系在电磁光谱的短波红外波段(1 400~2 500 nm)比可见光(400~700 nm)和近红外波段(700~400 nm)区域更为显著[13]。另一方面,在湿度敏感波长(吸水特性)下的吸收增加主要出现在波长为900 nm,1 400 nm和1 900 nm附近[14],是由于水中羟基(O-H)键特别的组合,但是在1 400 nm和1 900 nm附近,土壤的吸水特性被大气吸收所掩盖[15],因此,除了近距离的高光谱传感器外,其他仪器则无法对其进行测量。
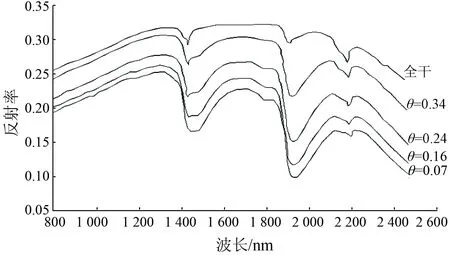
图1 θ-R 的变化关系[10]
HRS方法的主要先决条件是建立θ-R模型,该模型可用于从新样本的R估计θ。但是,开发具有合理精度的θ-R模型仍然是一项艰巨的任务,因为R不仅取决于θ,而且还受土壤的颜色、结构、矿物成分、有机质含量、粒度分布、表面粗糙度、干燥度以及测量条件的影响[16-19]。近几十年来,已有许多学者结合模型法对θ-R关系进行了研究,Bablet等[20]基于MARMIT(土壤反射多层辐射传输模型),将土壤反射光谱与土壤含水量以及水膜厚度建立联系,反演得出更高精度的土壤含水量; Gao等[21]测量了来自江苏省东台东北部潮滩的土壤样品的多角度反射率后基于粒子群优化算法,利用土壤光谱双向反射模型测出土壤表面的光谱特征,并通过引入土壤的等效水膜厚度来反演出更高精度的土壤含水量。虽然许多结合模型的θ-R研究方法都获得不错的结果,但大多数使用的都是经验模型,而不同的条件下使用经验模型也会产生许多不同的情况,还不能达到稳定的效果。因此,本文对现有的推导θ-R关系的方法进行了综述,并对它们的潜力和局限性进行了分析。
本文将建立θ-R关系的方法分为以下4类: 光谱反射率法(Ⅰ类)、函数法(Ⅱ类)、模型法(Ⅲ类)和机器学习法(Ⅳ类)。图2描述了现有θ-R关系的不同分类方法。

图2 θ-R关系的不同分类方法
1.1 波谱反射率法
1.1.1 相对反射率法
刘伟东等[22]证明了简单线性和非线性函数估算土壤含水量的效用,并描述了土壤在每个波段的反射率R与相对反射率R*(在非干燥条件下)之间的关系,公式为:
θ=a0R*+b0
,
(1)
θ=d0lg(R*+e0)+c0
,
(2)
式中a0,b0,c0,d0和e0为辅助参数。在低于临界水平的低湿度条件下,即在干燥条件下(θ=0),R*=1时,上述方程可修改为:
θ=a0(1-R*)
,
(3)
。
(4)
1.1.2 反射率指数法
一般来说,光谱反射率指数表示2个或2个以上波长的光谱反射率值的组合[22],可以是特定波长下光谱反射率的值(spectral index, SI)或它们变量的比值指数(ratio index,RI)、差分指数(difference index,DI)、导数(derivative,Der)和归一化指数(normalized difference index,NDI),通过一系列简单快速的计算,就可增强并获取相应目标土壤含水量的光谱特征,十分方便。公式分别为:
θ=a(λi,λi+1)+b(λi,λi+1)SI
,
(5)
,
(6)
DI(λi,λj)=R(λi)-R(λj)
,
(7)
,
(8)
,
(9)
式中:λi和λi+1为2个连续的波长;λj为与λi不连续的波长;a和b为辅助参数。在这类方法中,式(5)表示的是特定波长下光谱反射率的值; 式(6)表示的是比值指数法,即2个离散波长的反射率比值,如基于1 300 nm和1 450 nm波长的土壤含水量指数法(WISOIL); 式(7)表示的差分指数法和式(8)的导数法均由刘伟东等[22]提出,2种方法都尽量减少其他混杂因素的影响,以提高R对θ的敏感性,导数法近似于2个连续波长之间的有限差分而不是算术差分,当在计算中使用连续波长,即当λi+1=λj时,差分指数法和导数法则会产生相同的结果; 式(9)所示的归一化指数法是2个特定波长下的差值与反射率值之和的比值,如基于1 800 nm和2 119 nm波长的归一化土壤含水量指数[1]就属于归一化指数法。
刘伟东等[22]比较了相对反射率法、导数法和差分法估算土壤含水量的性能,得出一阶导数法估算土壤含水量优于其他方法的结论。最近,Tian等[23]建立了基于辐射传输的模型支持下的短波归一化指数(shortwave normalization index,SNI)用于土壤含水量估算,经验证,在土壤干燥阶段过程中,SNI指数所使用的分割方法显著提高了土壤含水量估计精度; Yue等[24]通过使用短波红外波段的不同吸水率特性,评估了3种标准化短波红外差异裸土水分指数(normalized shortwave-infrared difference soil moisture indices,NSDSI)估算裸土的含水量,得到2个短波红外波段比单一短波红外波段对裸土湿度估计更准确的结论; 另外,Fabre等[25]提出另外2个新的归一化指数,即使用近红外和短波红外波段从线性和非线性角度估算土壤含水量,线性回归法使用的是2 076 nm和2 230 nm的波长(R2=0.87;RMSE=4.4),而非线性回归法是基于2 122 nm和2 230 nm的波长(R2=0.74~0.85;RMSE=4.8~6.2),经过比较得出非线性回归法估算土壤含水量的结果要优于其他方法的结论。
1.1.3 反射率指数模型法
Lobell等[26]提出的物理模型解释了湿润状态下θ与R之间的关系,公式为:
R=Rsat+(Rdry-Rsat)exp(-cθ)
,
(10)
式中:Rsat和Rdry分别为水分饱和与干燥土壤状态下的土壤光谱反射率;c为R随θ的变化率。
除θ外,模型中的所有参数均与波长有关,还尝试将R表示为分数形式,用饱和曲线S代替θ,f为反射辐射表面积百分比,从而简化了不同土壤状态下的反射率模型,饱和曲线S的公式为:
。
(11)
1.1.4 反射率物理模型法
van Genuchten[27]提出描述基本电位h与θ关系的一种常用经验模型; Nolet等[28]在此基础上提出了用R代替模型中基本电位h的方法来描述θ-R之间的关系。公式为:
,
(12)
式中:θs和θr分别为残余含水量与饱和含水量;m和n为辅助参数。
1.2 函数法
Whiting等[29]将反高斯函数g(λ)与土壤光谱反射面相结合来估算土壤含水量,其反射面积A和振幅Z的参数与θ相关联。当使用短波红外波长进行计算时,辅助参数与反射面积A高度相关,2 800 nm左右的波长范围对其影响较大。g(λ),A和Z的计算公式分别为:
,
(13)
,
(14)
Z=Rλ0-Rλi
,
(15)
式中:λ0和λi分别为光谱反射面中心和拐点处的波长;σ为从光谱反射面区域中心到拐点的距离;erf(·)为误差函数。
1.3 模型法
1.3.1 概念模型
Philpot[30]提出了一个类似于Lobell等[10]的简单模型来描述光谱反射率,包括水面的菲涅耳反射率Rw、土壤颗粒的反射率Rs、液态水的吸收系数aw和光通过孔隙仪的日平均光程d,公式为:
R=fwRw+(1-fw)Rsexp(daw)
,
(16)
式中fw为水面反射辐射的表面积分数百分比。近红外波长范围的吸收系数值aw可以从Segelstein[31]和Kou等[32]的研究中获得。
1.3.2 光学模型
Nolet等[33]针对小面积湿润土壤反映出来的土壤反射率的变化很小,因而忽略了该部分造成的影响,并提出了一个基于兰伯特定律的针对沿海海滩砂砾进行分析的简单指数模型,公式为:
R=βRsexp(-daw)
,
(17)
式中β为湿润的海滩砂砾发生散射造成光谱反射率降低的影响因子。
1.3.3 线性物理模型
Sadeghi等[34]提出了一个简单的线性物理模型,该模型将土壤反射率即吸收与散射系数之比转换为干燥与饱和状态下土壤反射率的比值,公式为:
,
(18)
式中ω为干燥和饱和条件下土壤的散射系数之比。
1.4 机器学习法
深度学习法包括几种统计和机器学习方法,即多元线性回归法(multiple linear regression,MLR)、逐步多元线性回归法(stepwise multiple linear regression,SMLR)、主成分回归法(principal component regression,PCR)、偏最小二乘回归法(partial least squares regression,PLSR),支持向量机回归法(support vector machine regression,SVMR)、多元自适应回归样条法(multiple adaptive regression spline,MARS)和人工神经网络法(artificial neural network,ANN)。
Dalal等[35]使用MLR建立θ-R之间的关系,而王涛等[36]则采用了SMLR分析它们之间的关系,但这2种方法都存在一个缺点,即只用了某些特征波长点的光谱信息, 忽略其他点的信息,从而造成信息丢失, 导致模型的过适应性。PCR方法很好地解决了这个问题[37],PCR涉及到数学过程,通过正交变换将多个可能相关的变量转换为多个不相关的变量,这类变换可以通过数据协方差矩阵的特征值分解或数据矩阵的奇异值分解来实现。与PCR类似的方法是PLSR方法[38],它们最显著的特点是利用了全部的光谱信息,在PLSR中,预测变量和响应变量都被用于建立预测能力最强的分数,PLSR算法集成了压缩和回归步骤,并选择了连续的正交因子,使预测变量和响应变量之间的协方差最大化,从而提高了预测精度,因此该方法在土壤光谱研究中广受欢迎,并已被广泛用于估算土壤含水量[39]。
MARS[40],ANN[41]和SVMR[42]作为强大的非参数预测工具,其性能也被广泛用于检验线性和非线性θ-R间的关系。SVMR是一种基于核的学习方法,将输入数据映射到高维特征空间,在SVMR中,训练数据被用来获得一个损失函数,根据训练数据的最大偏差映射输入数据,利用损失函数作为与实际值“差距”的度量,对大于损失函数的误差进行剔除,以获得较低复杂度的训练数据子集,从而提高估算精度。尚天浩等[43]对盐渍地区土壤原始光谱反射率进行多种数学变换,运用逐步回归(stepwise regression, SR)和灰色关联度(grey correlation degree, GCD)筛选敏感波段,比较MLR,PLSR和SVMR这3种方法模拟土壤含水量的精度情况,得出SVM模型为供试土壤含水量拟合的最佳模型,能够准确获取重度盐渍化研究区土壤含水量状况的结论; 吴士文等[44]也对比分析不同光谱预处理方法与PLSR,SVMR建模方法两两组合条件下对土壤含水量的精度预测,结果表明, 同一光谱预处理方法的SVMR模型预测精度均高于PLSR模型,因此也间接表明了SVMR法在某些方面优于一般的线性回归统计学习方法。
MARS[45]是一种非参数回归技术,它利用基函数自动建立预测-响应联系(即不需要任何假设)。为了开发基函数,输入数据空间被细分为具有特定回归模型(分段线性回归)的区域或样条曲线。在进行分段线性回归时,允许回归模型的斜率沿预测轴改变n个节点,将由线性和非线性组合以及二阶和三阶变量因子组成的基函数,作为新的预测变量用于建模,通过一个严格的前向和后向逐步查找过程,找到一个具有最佳节点数和基函数的模型。正向逐步法通过增加基函数来构造一个过拟合模型,而反向逐步消除法消除了对模型精度贡献不足的函数,相比于线性回归模型,MARS模型更加灵活。
ANN[46]是一种用于模拟“输入-输出”联系的技术。它由各种相互关联的计算单元(节点或人工神经元)组成,可分为学习和优化2个阶段。在学习阶段,人工神经元则聚合成隐藏层,这些层能够对输入进行不同的转换,然后通过调整人工神经元相互影响的“权重”及其相互关系结构来表征系统行为的输入-输出关系; 在优化阶段,ANN通过对已知信息的反复学习训练,并逐步调整改变节点权重,达到处理信息、模拟输入输出信息的目的。
2 土壤含水量估测方法的潜力与局限性
为了简要讨论通过R来估计θ的不同方法在精度、复杂性、辅助数据要求、不同遥感模式下的可操作性以及对土壤类型的依赖性等方面的潜力和局限性,对描述θ-R关系的不同方法的性能进行了对比,结果如表1所示。这些方法是根据土壤的相关漫反射光谱研究所得出的,尽管比较这些研究的结果是不太合理的,因为它们是在不同的土壤和测量条件进行的,但通过比较可以大致了解各类方法下θ-R之间的相关性以及不同方法的优缺点。未来的研究应该尽可能在保证处于相同的基础条件下对不同方法进行定量比较,使结果更为合理恰当,从而进行更有意义的评估。

表1 利用高光谱特征估计土壤含水量的不同方法性能比较
表1中相对反射率法考虑了不同土壤类型、粗糙度和结构的具体特征,虽然它是经验性的,但在1944年主要验证光谱反射率波长的实验室条件下,该方法是有效的,但却不适用于野外条件,因为野外条件下土壤的反射率被大气吸收所掩盖,此外,该方法还依赖于每种土壤在干燥条件下的光谱反射率信息,如在土壤样品干燥时,光谱反射率会随方向相位角变化而变化[49],但由于空间和时间上的异质性使得干土光谱反射率信息难以获取,因此该方法也难以实现。差分和导数法使用多个波段进行计算,土壤类型对其产生的影响较小,土壤总反照率的损失也降低了,更有利于波段组合计算,因此差分和导数法相对更为稳定。在导数法中,样品光谱在不同波长处的反射率值可以相互关联,因此不需要先验的土壤信息,且该方法不需要考虑水蒸气吸收波长的影响,因此能够与野外、机载和星载测量方法结合使用。然而,由于使用具有强相关性的连续波段,导数法会带来冗余的光谱信息,相比之下,差分法可以使用相关性较小且光谱分离程度较低的具有独立信息的波段进行计算。指数模型最适合用短波红外波段的光谱反射率来估算土壤质量θm或体积含水量θv,它们与可见光和近红外波段结合使用可能不适合于土壤体积含水量低于20%的情况,且其受不同土壤类型的影响,而为了减少土壤类型的影响,目前的指数模型已发展为使用土壤饱和含水量来代替土壤质量含水量θm或体积含水量θv来计算; 土壤物理模型则需要残余含水量θr和饱和含水量θs作为初始信息输入,但其应用只局限于θr-θs范围内。
反高斯函数法是通过近红外和短波红外区域1.2~2.5 μm的反射率下降来估计水分含量,基本吸水率在2.8 μm处的扩散,对其影响较少,因此,该方法可与所有高光谱反射率测量模式结合使用。但是,它需要对光谱进行额外的预处理,以削弱短波红外区域的噪声,同时其面临难以确定的输入信息[50]。Philpot[30]所证明的简单的概念模型在实验研究中被发现是成功的,可以解释4种土壤类型的θ-R关系,但是这种模式是“肤浅”的,不足以令人信服。
光学模型法是一种简单的概念模型,无需考虑高光谱反射率,在土壤体积含水量的估算方面表现良好。线性物理模型简单、准确(尤其是在短波红外波段),不受限于单个波长,并且只需要少次的校准,因此,它被认为是一种最有前途的估计土壤含水量的方法,但是该模型仍需要在干燥和饱和土壤条件下测量的高光谱反射率进行校准,这也是该模型的难点之一。
尽管与其他方法相比,机器学习方法在计算上比较复杂,但在光学领域它们能够较好地证明θ-R之间的关系,并且无需考虑土壤类型。由于MLR中的预测变量必须是不相关的,不适合处理与高光谱反射率相关的多个共线光谱变量; PCR和PLSR方法都是通过正交变换来解决多共线问题的经典方法,但PCR只考虑了光谱信息,而PLSR方法不再直接考虑因变量与自变量的回归建模,而是对变量系统中的信息重新进行综合筛选,从中选取若干对系统具有最佳解释能力的新成分用于回归建模,经过这样的信息筛选,排除了对因变量无解释作用的噪声,不仅提高了其计算效率,使得计算结果更可靠[51-52]。但这2种经典的方法无法解释土壤光谱和属性之间的非线性效应(由于土壤的光谱复杂性),特别是在大型土壤光谱数据库中,在这种情况下,可以选择SVMR,MARS和ANN等替代技术来开发性能更好的高光谱反射率模型,SVMR方法解释了模型开发时过度拟合的原因[53],并由此产生了一个处理高维光谱变量的高效全球模型[54],然而,这种模型的识别是计算密集型的,因为它涉及2次规划和非线性方程组的求解[55]。MARS是一种非参数方法,更像是线性回归的一种扩展,它将高光谱反射率简单地转换为图像像素,因此,它被认为比经典的线性回归模型更灵活、更准确[56]。ANN模型相比其他方法拥有更好的性能,但是它容易过度拟合,并且结果过于依赖于初始化参数,因而不可避免地含有误差而无法保证对土壤含水量进行预测时有较高的精度[57]。
3 结论及展望
根据不同土壤光谱反射率与土壤含水量之间的关系,本文将θ-R研究方法分成4类,并从精度、复杂性、辅助数据要求、不同遥感模式下的可操作性以及对土壤类型的依赖性等方面分析了它们的潜力和局限性。大多数方法在试验区范围内能有效证明θ-R之间的关系,但方法的迁移性和扩展性还需要更多的实验验证。其中反射率指数法(除了差分法和导数法)、函数法和模型法在计算上有优势,但它们需要获得先验的土壤信息。在没有土壤信息的情况下,需要通过使用全部光谱反射率来估算土壤含水量,此时机器学习法更具优势,但是也取决于机器学习法在数据建模中使用的光谱数量的多少,数量过多则会影响计算效率。
针对以上存在的问题,笔者建议从以下几个方面进行改进或深入研究: ①使用高信噪比的改良仪器更好地测量土壤含水量(以减少大气变量的影响); ②改进对光谱反射率的预处理方法; ③增加简约模型对光谱变量的选择; ④新物理模型和机器学习算法的实现; ⑤物理模型(理论驱动)和机器学习算法(数据驱动)相结合以消除与土壤含水量不相关的光谱信息和冗余信息。
目前,所有现有的方法本质上都是通过经验模型反映得出θ-R关系,很少涉及不同土壤类型之间的联系变化。本文中大多基于漫反射光谱的土壤含水量研究方法也都是在温带土壤状态下进行的,温带土壤有机质的分解率较低,黏土矿物的比例大致为2∶1。在热带和亚热带土壤中建立θ-R关系的研究非常有限,因为在此条件下,土壤有机质分解较强,黏土矿物的比例基本为1∶1,黏土矿物比例不占优势,而由于土壤有机质和黏土矿物具有光谱活性,它们显著地影响光谱反射率,因此在温带土壤中推导的θ-R关系在热带和亚热带土壤应用中可能失效。目前国内外针对θ-R关系的土壤特性的研究相对较少,需要更进一步的研究。因此,未来对于θ-R关系的研究可以集中在比较不同方法在不同土壤类型下的应用,如建立不同类型土壤样本的公共光谱库等,以便更好地进行土壤含水量的估算,从而得到更准确的θ-R关系。
——缺陷度的算法研究

