基于某振动场景的直升机飞控系统陷波器设计

付益恺，孟文杰，何 野

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

在直升机飞行控制系统的设计中，如何抑制不同频率点的振动噪声一直以来都是系统设计的重点和难点。在实际的试验/试飞过程中，在地面试车或滑行阶段，常会出现不同频率的低频异常振动。

对于振动噪声的抑制，低阶的IIR低通滤波器(如二阶巴特沃斯低通滤波器)是一种可供考虑的选项。这种滤波器的优点就是设计简单，运算速度快，但也存在两个明显的缺点：一是造成较大的相位滞后，这种滞后可能导致姿态的超调甚至发散；第二点是由于真实的运动信号有非周期项，频域上会铺满整个频谱，低通滤波器的引入使得这部分信号失真。使用带阻滤波器则可以完美解决以上两个问题。

带阻滤波器可以分为很多种类型，在直升机振动抑制领域，陷波滤波器成为热点。陷波器通常指二阶带阻滤波器，其幅频特性曲线如图1所示。其设计简单程度和运算速度与二阶低通滤波器相当，适合工程应用。

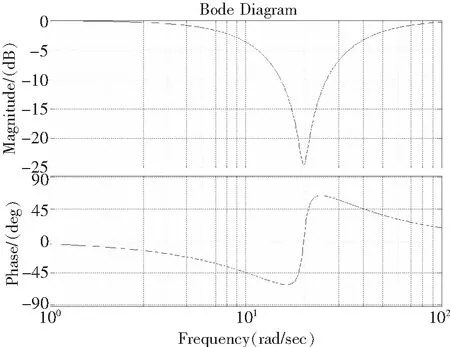
图1 陷波器幅频特性曲线

理论上，滤波器阶数越高越接近理想滤波器，但滤波器阶数达到一定值后再增加阶数，其逼近程度并不再显著提高，但计算量依然增加，所以理论上不再需要无穷大的阶数。

实际编程中，随着阶数无限升高，更根本的问题是计算机积累误差凸显，将使其与理想滤波器相去甚远，最终时域幅值严重失真，所以实际应用中滤波器阶数也不是越高越好。

本文针对某型直升机实际试飞过程中出现的振动问题设计了一种二阶带阻陷波器，并进一步从理论分析和数值仿真的角度对干扰信号的抑制效果进行了验证。

1 振动场景分析

直升机振动的源头主要包括旋翼等旋转部件周期激励及气动力等引起的宽带随机激励。以某型机为例，周期激励对应的振动主要包括旋翼1(4.3 Hz)、5(21.5 Hz)，尾桨1(19.8 Hz)、4(79.3 Hz)等；紊乱的气动力引起随机激励产生以全机/部件模态频率为特征的振动响应，模态响应因存在阻尼，一般情况下幅值很低且可以衰减。

正常情况机体在宽带随机激励下存在低量值、可衰减的振动响应(频率成分很多，幅值<0.04 g)。直升机处于增稳模式时，低量值的振动响应逐步增大，同时角速率、主桨舵机输出、周期变距角等的幅值逐步增大，小量值的振动响应通过角速率反馈耦合到飞控系统中，进一步反映到飞控系统的指令及舵机输出中，主桨舵机作用到旋翼，形成周期激励作用到机体上，从而导致全机异常振动(见图2)。飞控系统不是产生振动的源头，但飞控系统的角速率反馈是异常振动的关键途径，为异常振动的增大和持续提供能量。

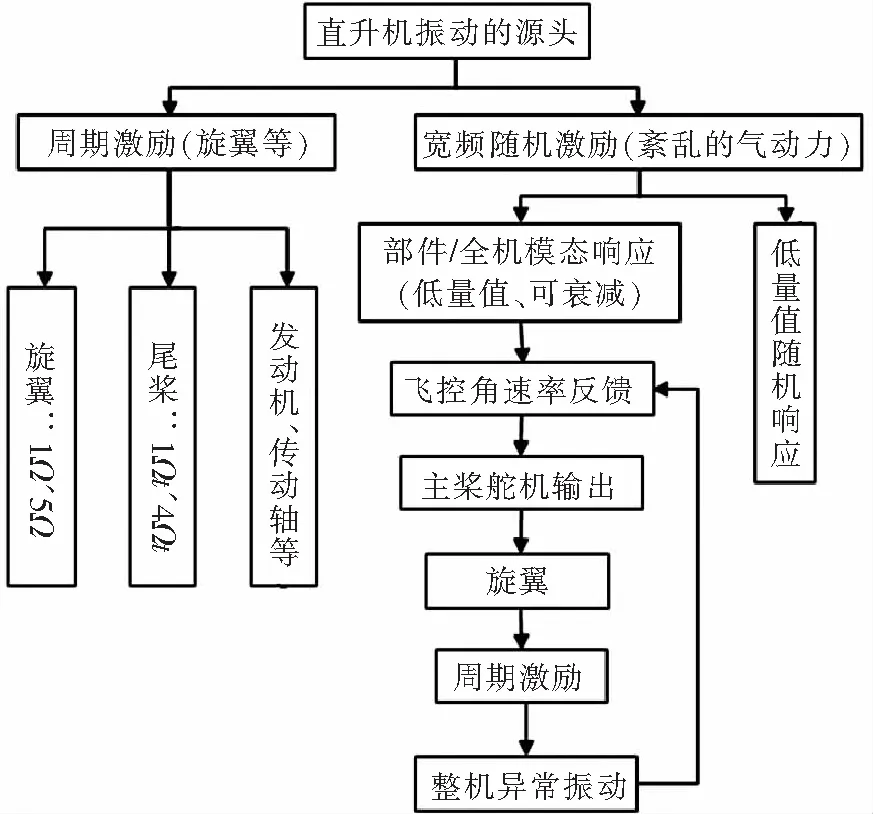
图2 异常振动场景分析

在上述场景引发的直升机异常振动中，飞控系统增稳模式的角速率反馈是振动增大的途径。想要抑制振动的加剧，最佳的解决方法就是切断异常振动到飞控舵机输出之间的反馈，从而切断异常振动增大的途径。

为解决上述问题，本文基于无限冲击响应(IIR)滤波器的设计原理，设计了一种陷波滤波器，切断了机体振动到飞控系统间的耦合，抑制了宽频随机激励引发的直升机异常振动。

2 滤波器模型

在陷波滤波器的设计中，最常使用的是理想陷波器、巴特沃斯陷波滤波器和高斯陷波滤波器。三种陷波滤波器的参数模型如表1所示。

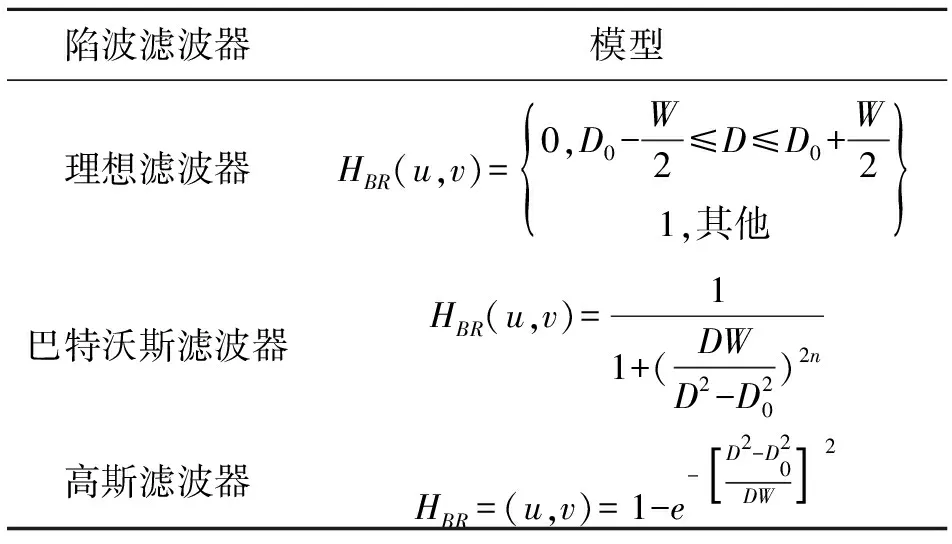
表1 常用陷波滤波器模型

理想滤波器、二阶巴特沃斯陷波滤波器和高斯陷波滤波器的透视图如图3-图5所示。

由三种陷波器的透视图和模型可以看出，理想滤波器在以(,)为圆心，为半径的圆内截断所有频率，在圆外通过所有频率，其滤波非常尖锐；而高斯滤波器的滤波则非常平滑。巴特沃斯滤波器介于两者之间，当巴特沃斯滤波器的阶数较高时，接近于理想滤波器，阶数较低时，则接近于高斯滤波器。

理想滤波器和高斯陷波滤波器都是线性滤波器，能够有效地抑制噪声，平滑图像，计算量较大，常用作图像处理，并不常被应用于工程实践中。

在直升机飞控系统的陷波器设计中，本文采用了巴特沃斯滤波器的形式。该滤波器的特点是通频带内的频率响应曲线最大限度平坦，没有起伏，而在阻频带则逐渐下降为零。在振幅的对数对角频率波特图上，从某一边界角频率开始，振幅随着角频率的增加而逐渐减少，趋向负无穷大，它在通频带内外都有平稳的幅频特性。

3 仿真分析

3.1 二阶巴特沃斯滤波器

本节利用实际试飞数据，通过数值仿真，进一步验证所设计的陷波滤波器对异常振动的抑制效果。

为测试二阶巴特沃斯陷波器的滤波效果，首先通过一组测试信号进行陷波滤波器的测试。由于在实际试飞中，4.3 Hz和13 Hz这两个频率的随机激励常被引入到飞控系统的角速率反馈回路中，因此，下文中将重点针对这两个频率的扰动进行仿真验证。

通过图6仿真结果可知，将同时包含4.3 Hz和13 Hz两种频率的信号进行陷波滤波，通过陷波滤波器后，信号仅剩下4.3 Hz。同理，图7也能获得相同效果。

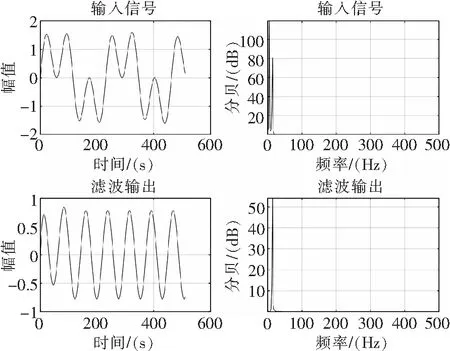
图6 陷波滤波器频率4.3 Hz

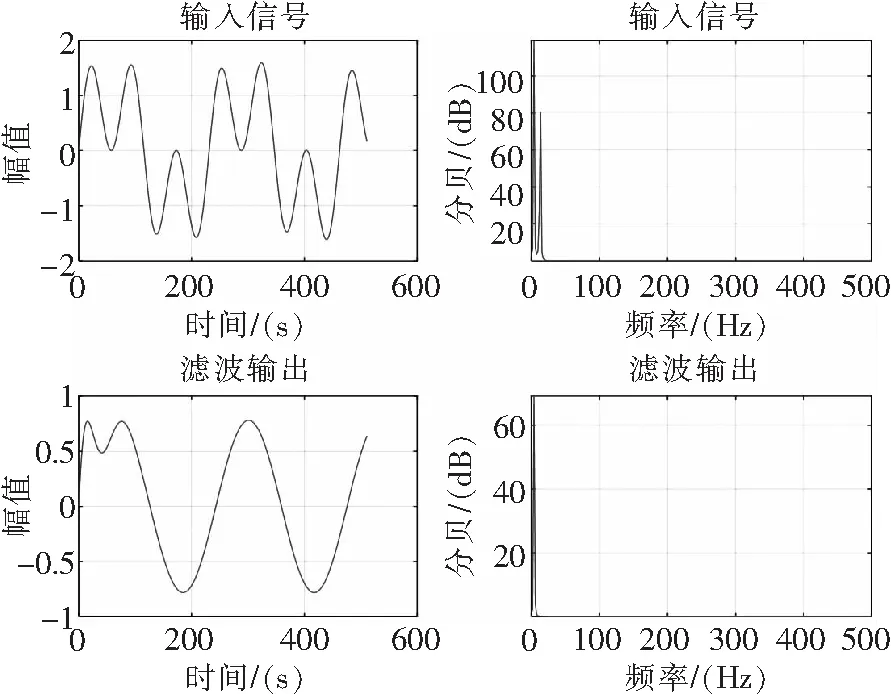
图7 陷波滤波器13Hz

现加入实际试飞数据进行仿真，仿真效果见图8、图9。如图所示，控制律引用角速率数据时，其幅值已衰减为原始采集值的20%至25%，陷波滤波器滤波效果良好。

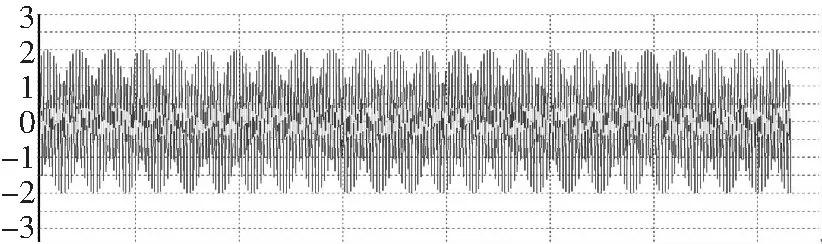
图8 陷波前——角速率信号

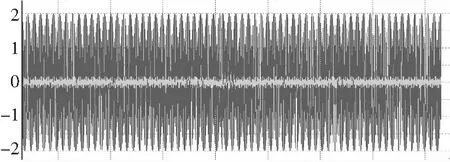
图9 陷波后——角速率信号

3.2 改进算法

二阶陷波滤波器适合工程应用，但由于每次飞行时直升机的挂载、重量、重心等状态均不同，且传感器的测量精度有限，会存在一定误差，造成直升机在不同状态下振动干扰基频带的中心频率可能也会存在一定偏差。因此，有必要使用带宽更宽的带阻滤波器进行飞控系统的噪声抑制。

由傅里叶变换的对称性可知，零相移滤波器必须关于原点对称，一个中心位于(,)的陷波器在位置(-,-)必须有一个对应的陷波，可以称之为陷波对。

陷波带阻滤波器可以由若干个以(,)为中心的高通滤波器对的乘积来构造。设计原理如下：

1)一个以(,)为中心的高通滤波器完成对频率(,)和(-,-)的筛选；

2)频域将多个陷波对相乘，意味着空间域与这些陷波对逐个卷积，依次完成对各个陷波对中心频率的筛选。

依据上文二阶陷波滤波器的结构，就能推导出包含多个陷波对的陷波带阻滤波器，其滤波器结构如下：

，(，)=

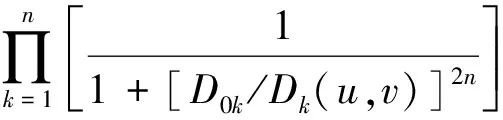
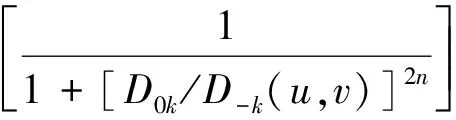
(1)

其中，0是每个陷波对的陷波带宽。

理想、巴特沃斯和高斯陷波带阻滤波器的透视图如图10所示。

根据式(1)设计一种陷波频率为4.3 Hz和13 Hz的四阶陷波带阻巴特沃斯滤波器，利用实际试飞数据，对三轴角速率注入1 Hz至15 Hz的激励，输入和输出对比如图13-图15所示。

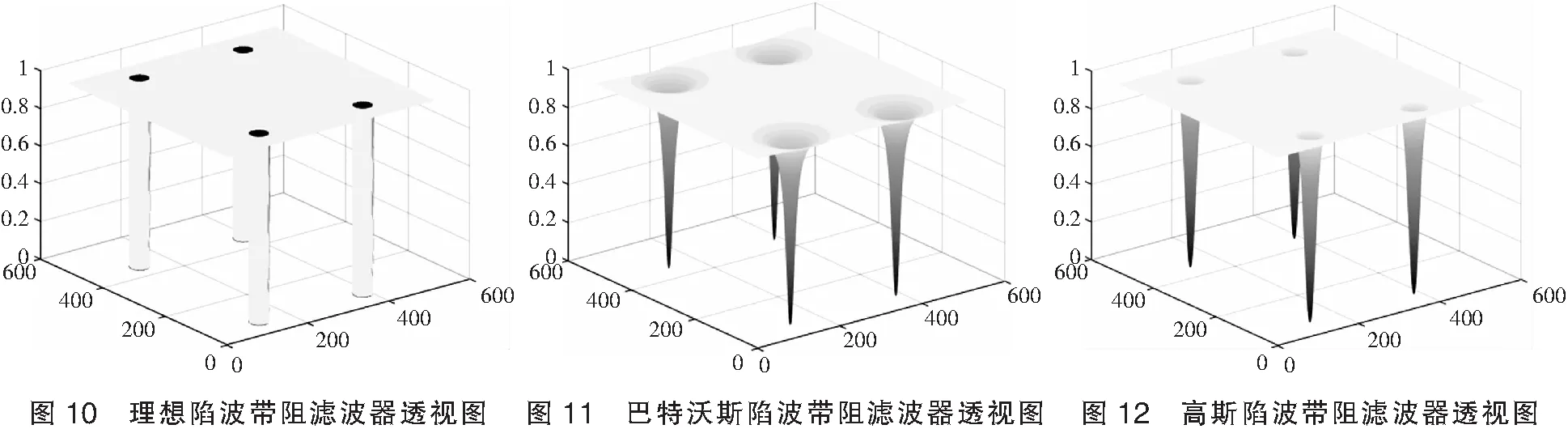
图13 俯仰角速率

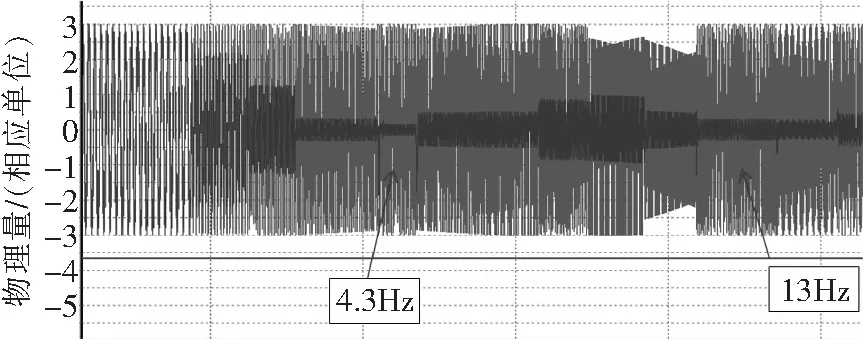
图14 横滚角速率

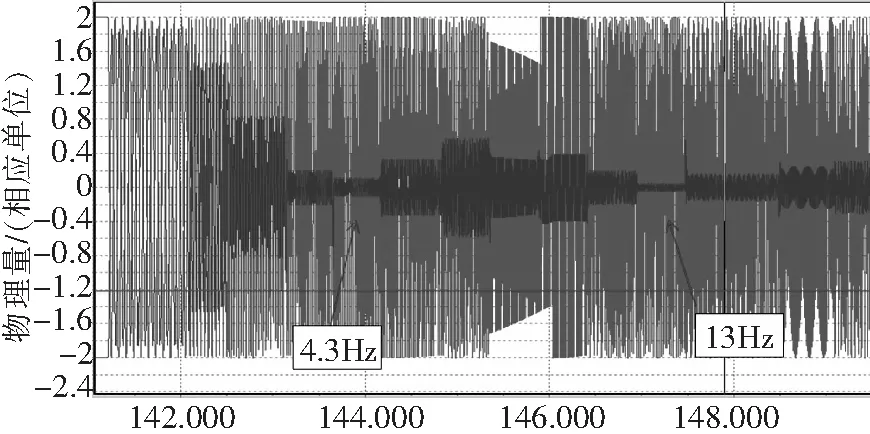
图15 偏航角速率

由仿真结果可知，在4.3 Hz和13 Hz附近，角速率信号原始输入幅值衰减为激励值的10%以下，陷波带阻滤波器滤波效果良好，可以有效抑制多组不同频率随机激励耦合入飞控系统反馈回路所造成的异常振动。

4 结论

直升机的振动是由于旋翼本身的特性而与直升机长期共存的固有问题。通常来说，直升机的振动可以分为周期激励和随机激励，而随机激励常会随反馈信号进入飞控系统的反馈控制回路，存在加剧全机异常振动的风险，给飞控系统的设计带来了困难。本文针对该问题分别设计了二阶陷波滤波器和四阶陷波带阻滤波器，该滤波器具有以下优点：①算法结构简单；②计算量低；③工程应用性强。并且分别从理论分析和数值仿真验证的角度，验证了上述滤波器算法的滤波精度和效果，为解决随机激励进入直升机飞控系统反馈回路的问题提出了可供参考的途径。