一种利用子猫群交互的改进猫群优化算法

李松阳，于海鹏，王 淼

(河南工程学院 软件学院，河南 郑州 451191)

猫群优化(cat swarm optimization，CSO)算法是2006年Chu等[1]基于对猫群行为的观察，为解决连续和单目标优化问题，设计并提出的一种新的群体智能算法。猫群优化算法采用迭代的方式优化问题，具有易实现、能全局搜索、收敛速度较快等优点。作为新兴的群体智能算法，猫群优化算法在国外引起了众多研究者的关注。Pyari等[2]对猫群优化算法进行了扩展，提出了一种新的多目标进化算法。Tsai等[3]提出了一种并行猫群优化算法，在猫群数量和迭代次数较少的条件下实现快速收敛，并进一步研究了增强并行猫群优化算法，比如在猫群跟踪模式中引入田口法(Taguchi method)，提高猫群优化算法的收敛速度和全局搜索能力[4]。Tsai等[5]结合猫群优化算法和人工蜂群算法提出了一种混合优化算法框架。猫群优化算法与其他群体智能算法结合的混合优化算法开始发展起来。Vivek等[6]提出了一种将猫群优化算法、粒子群优化算法和遗传算法结合的混合算法用于解决情感识别问题。Nanda[7]提出了一种结合猫群优化算法和小波神经网络(wavelet neural network)的混合算法用于预测混沌和非线性时间序列。Sarswat等[8]提出了一种结合猫群优化算法、遗传算法、模拟退火算法的混合算法用于解决社交网络问题。在猫群优化算法提出后，众多学者针对该算法也提出了很多改进的方法。Sharafi等[9]提出了一种基于猫群优化算法的二进制离散优化方法，大幅提高了0/1背包问题的准确率。Siqueira等[10]提出了一种基于布尔算子的二进制猫群优化算法 ，在髙维0/1背包问题上具有较好的可行性。现实中，猫群优化算法在背板接线问题、天线阵综合等方面有众多应用[11-12]。

在国内，猫群优化算法也吸引了众多研究者。在猫群优化算法改进方面，杨进等[13]在猫群的跟踪模式中引入交换子和交换序及随时间变化的分组率用于求解旅行商问题。裴小兵等[14]引入了基于线性混合比率的猫行为模式选择，依据迭代次数合理分配局部搜索和全局搜索的比例。陶亚楠等[15]依据当前迭代次数和最大迭代次数的比值来调节猫群优化算法的分组率，从而使算法自适应性增强。陈超泉等[16]提出了一种具有Logistic函数特点分组率和惯性权重的自适应方法，该方法对于猫群优化算法来说在收敛速度及求解精度方面都有一定程度的提高。

以上国内外的研究虽然都在一定程度上实现了猫群优化算法的改进，但优化方向主要集中在算法的分组率、惯性权重因子和变异率等关键参数的选择策略上。由于猫群优化算法在迭代时分为搜寻模式猫群和跟踪模式猫群，故如果只对猫群优化算法中分组率即猫群划分策略进行改进，虽然能改善其性能，但两种行为模式猫群间的交流也会影响该算法的收敛能力，并且每只猫的学习模式固定，对算法性能的提升有限[17]。

本研究提出了一种基于子群信息交互的改进猫群优化算法(IICSO)。该算法采用动态分组策略调整分组率，从而实现搜寻模式猫群和跟踪模式猫群的动态调整。在迭代过程中搜寻模式猫群和跟踪模式猫群需要交流学习，充分发挥不同猫群优势，使算法具有了良好的全局探索能力和较快的收敛速度。最后，通过10个标准测试函数验证了该算法在收敛速度和寻优精度方面都具有显著优势。

1 改进的猫群优化算法

1.1 原始猫群优化算法流程

猫群优化算法是一种模仿猫群生活习性的智能算法。猫群有跟踪和搜寻两种不同的行为模式。搜寻模式下的猫大部分时间在休息，同时也在观察周围环境，总是保持警觉；跟踪模式下的猫发现猎物后，在追逐目标时会快速移动。

在猫群优化算法中，每只猫对应了待优化问题的一个解。每只猫都有自身的适应值、标志和位置。适应值用来评价猫群中每只猫位置的好坏，标志用来区分每只猫的跟踪和搜寻行为模式。对于第i只猫来说，其位置Pi是定义在解空间中的一个N维向量，pij表示第i只猫位置Pi的第j个维度。位置Pi的每一维(pij)有自身的速度(vij)，则vij构成的N维向量组成了第i只猫的速度Vi：

Pi=|pij|，j=1，2，…，N，

(1)

Vi=|vij|，j=1，2，…，N。

(2)

猫群优化算法的基本流程如图1所示。在N维解空间中，通过随机的方式设置每只猫的位置和速度，形成一定数量的猫群。初始化猫群的分组率等参数，计算每只猫的适应值，并记录最优适应值到pbest中。根据分组率将猫群随机划分为跟踪和搜寻两种行为模式。根据猫的标志，对跟踪行为模式的猫执行跟踪流程，对搜寻行为模式的猫执行搜寻流程。待跟踪流程和搜寻流程结束后，计算每只猫的适应值，并记录最优适应值到pl中。比较pbest和pl的大小，更新pbest。若满足结束条件，则终止算法，否则重新分组迭代。

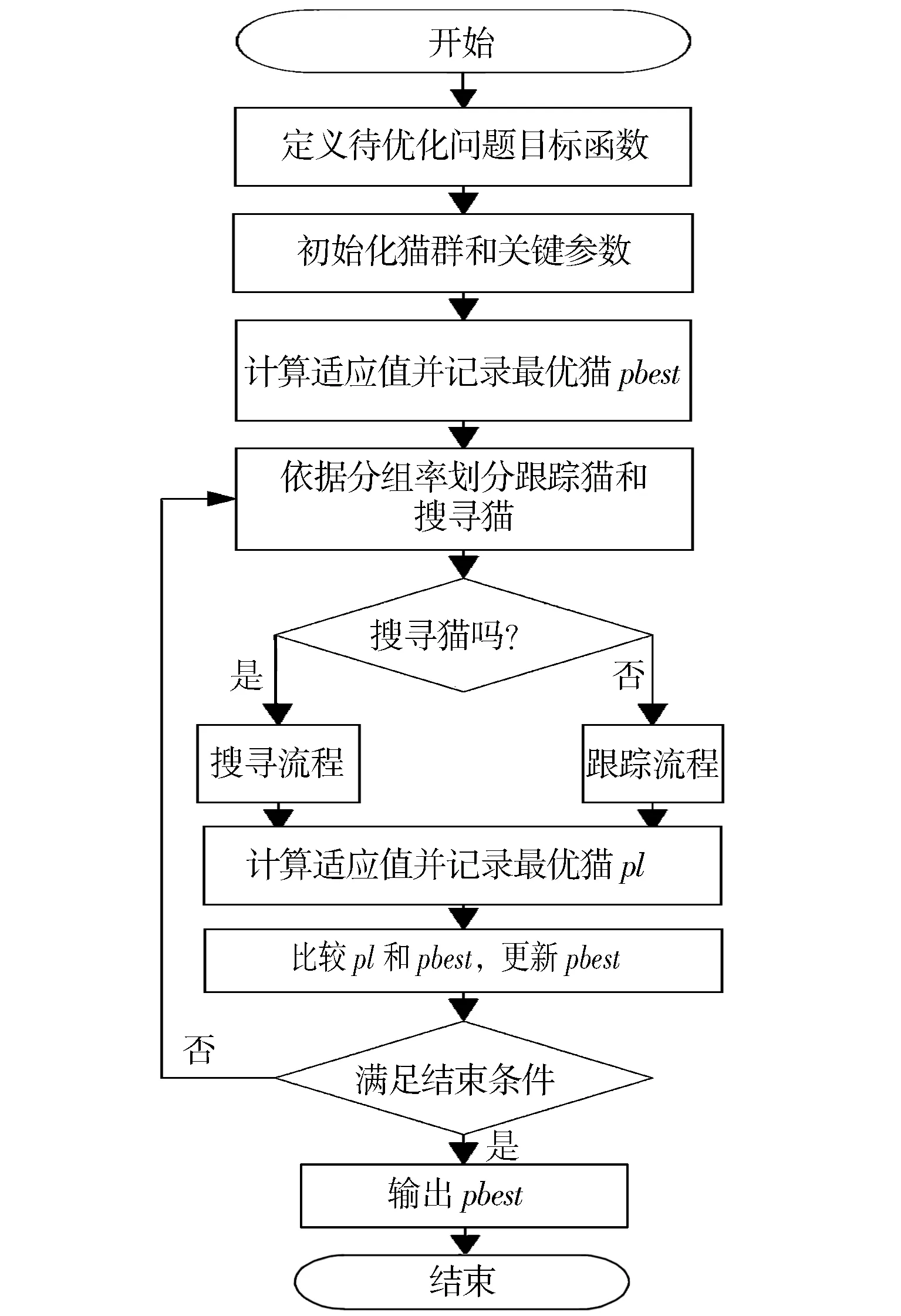
图1 猫群优化算法流程Fig.1 Cat swarm optimization algorithm flow chart

1.2 跟踪模式流程

在跟踪行为模式下，猫发现猎物后会快速移动，向目标靠近。跟踪模式是对猫追踪目标时一系列行为的建模，每只猫会调整移动速度从而调整位置，持续朝着目标移动。

跟踪流程如下：

(1)更新处于跟踪模式的第i只猫的速度vij：

vij=ω×vij+rand×c×(pbestj-pij)，j=1，2，…，N，

(3)

式中：pbestj为猫群中最优适应值猫的位置的第j维；ω为惯性权重因子；rand为均匀分布在[0,1]的随机数；c为事先确定的0～2的常数。

(2)如果设置了猫群优化算法猫速度区间，则检查更新后的猫速度有没有超出预先设定的速度范围。

(3)更新处于跟踪模式的第i只猫的位置pij：

pij=pij+vij，j=1，2，…，N。

(4)

1.3 搜寻模式流程

在搜寻行为模式中，猫大部分时间在休息，但也在观察周围环境，总是保持警觉。如果想移动位置，猫在观察周围环境后，总是小心翼翼非常缓慢地移动到新位置。猫群搜寻模式是模拟猫四处搜索并寻找下一个位置的模型，它有3个关键参数，即记忆池、变异率、变化数。

记忆池：用SMP表示，定义每一只猫的搜寻记忆大小，用来存放此猫搜索过的能够记忆的所有位置点。

变异率：用SRD表示，定义猫位置变化时每一维能够变化的范围。

变化数：用CDC表示，定义猫位置变化时可以发生变异的维度数目，该数目不能大于解空间维度N。

搜寻流程如下：

(1)处于搜寻模式的第i只猫，把该猫复制K份到SMP(K=SMP)。

(2)K份副本中，保留其中1份副本不变，其余K-1份副本根据第i只猫的CDC值，随机选择与CDC值数目相同的维数进行位置变异：

pij=(1±SRD)*pij，pij∈pi。

(5)

(3)更新计算SMP中每个副本的适应值。

(4)从K份副本中，选择适应值最优的副本替换第i只猫的位置，从而实现猫对空间的搜索与位置更新。

1.4 分组率动态调整策略

猫群优化算法中分组率是十分重要的参数，是猫群中执行跟踪模式的猫占猫群的比例，能极大地影响算法的开拓和搜寻能力。分组率(MR)动态调整策略见公式(6)：

(6)

式中：MRmax是分组率最大值；MRmin是分组率最小值；iter表示当前的迭代次数；MaxIt为最大迭代次数；a1和a2是调节因子，控制MR的变化速度。

图2展示了a1和a2不同取值时MR的变化情况：在迭代前期MR变化较为平缓，有较多的猫被划分为跟踪行为模式，提高了全局搜索能力；在迭代中后期，MR快速降低，有较多的猫被划分为搜寻行为模式，提升了算法的局部搜索能力。

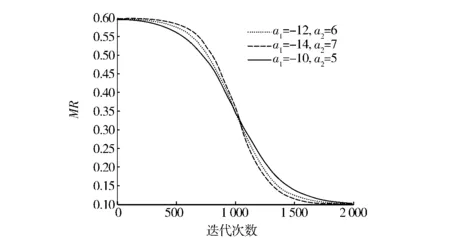
图2 MR变化情况Fig.2 Change of MR

1.5 子猫群信息交互策略

将整个猫群依据MR动态划分为两种行为模式后，不同行为模式猫群之间的信息交互也影响着算法效果。在图1展示的猫群优化算法流程中，执行搜寻模式的猫和执行跟踪模式的猫，它们的信息交互依赖于整个猫群最优适应值猫位置的更新，两种行为模式猫群之间不存在其他交互方式。本研究采用Rao等[18]提出的教与学优化算法强化两个猫群互相交流学习。首先比较两种行为模式猫群适应度值大小，拥有较优适应度的猫群为优秀猫群，另一个为普通猫群；然后从优秀猫群中随机挑选一个学习猫(Pl)，普通猫群中所有猫使用教与学优化算法学习阶段的规则向学习猫(Pl)学习，并产生新后代。学习方法如下：

(7)

式中：符号f(Pi)表示第i个猫的适应值；plj表示学习猫(Pl)位置向量的第j维；pij表示第i个猫(Pi)位置的第j维；γ为学习因子，是[0,1]的随机数。从公式(7)可以看出当学习猫(Pl)的适应值小于普通猫群中第i个猫的适应值时，第i个普通猫会远离学习猫(Pl)；当学习猫(Pl)的适应值大于等于普通猫群中第i个猫的适应值时，第i个普通猫会靠近学习猫(Pl)。 学习结束后采用公式(4)计算普通猫的新位置。当新位置的适应值优于原位置时，普通猫移动到新位置，否则不移动。

1.6 改进的猫群优化(IICSO)算法流程

步骤1： 初始化猫群及控制参数。

步骤2： 计算猫群中每个猫的适应值，同时更新此时的全局最优解pbest。

步骤3： 利用公式(6)计算分组率MR。 按照MR将猫群随机分为两部分,一部分执行搜寻流程， 另一部分执行跟踪流程。

步骤4： 执行搜寻流程，更新搜寻行为模式猫的位置；执行跟踪流程，更新跟踪行为模式猫的速度和位置。

步骤5： 两种行为模式猫群之间交流，普通猫群向优秀猫群中的学习猫Pl学习并产生后代，更新普通猫的速度，并依据公式(4)计算普通猫位置，判断普通猫是否满足移动到新位置的条件，如满足则移动，否则不移动。

步骤6： 计算每只猫的适应值，并记录最优适应值到pl中。 比较pbest和pl的大小，更新pbest。 若满足结束条件，则终止算法，否则重复步骤3重新分组迭代。

2 实验与结果分析

2.1 算法设置

为了充分比较CSO算法、ADSCSO算法与IICSO算法的求解精度和收敛速度，对这3种算法使用10个代表广泛的标准测试函数进行验证，测试函数范围限制和算法参数设置分别见表1和表2。这3种算法的机器配置为Windows 10操作系统，CPU为Intel(R) Core(TM) i7- 4700MQ 2.40 GHz，内存为8.00 GB。数据分析采用MATLAB R2020b软件。

表1 测试函数的数学描述Tab.1 Mathematical description of test function

表1(续)

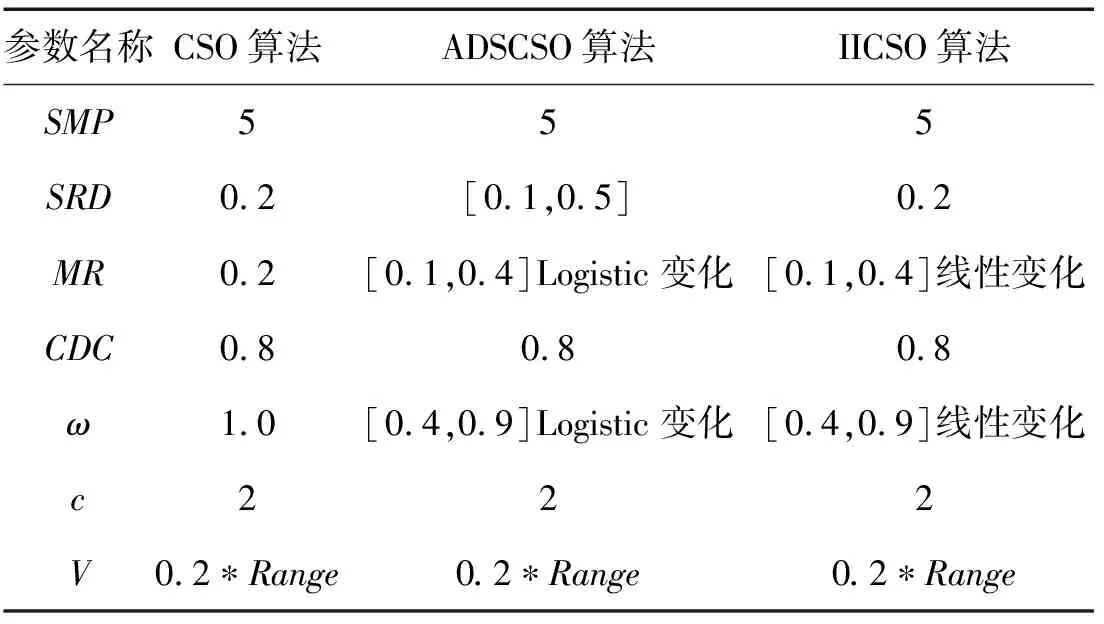
表2 不同算法参数设置Tab.2 Parameter settings of different algorithms

如表1所示，F1～F2函数属于板状函数(plate-shape)，除全局极小值外不存在局部极小值。F3～F6函数具有较多的局部极小值(many local minima)，使算法有陷入局部极小值的风险。F7函数是碗状(bowl-shaped)的，除全局极小值外，还具有与解空间维数相同的局部极小值，具有连续的、凸的和单峰的特征。F8函数是山谷状(valley-shaped)的，具有单峰，全局最小值位于一个狭窄的山谷。F9函数是单峰陡峭形态(steep drops-shaped)的，全局极小值相对于搜索空间的面积很小。F10函数具有多峰，在输入域的拐角处有尖峰等特征。

所有算法的相关参数如表2所示。对于所有算法，群体大小设置为 100，最大迭代次数是500。 每种算法在实验中独立运行20次，统计每个算法的测试函数平均值、标准差和最优值。平均值能够体现出算法的收敛能力，标准差能够体现出算法的稳定性。

2.2 结果与分析

表3为CSO算法、 ADSCSO算法与IICSO算法的对比结果。其中，平均值和标准差由20次独立运行后获得，黑体字表示算法获得的值在对应测试函数上是最好的。从表3可以看出,在板状函数F1、F2上，IICSO算法在高维测试函数F2(解空间20维)上的性能明显优于其他两种算法，但在低维测试函数F1上(解空间2维)，CSO算法更具有优势。在具有较多局部极小值特征的测试函数F3～F6和F10上，IICSO算法也具有明显优势。在函数F3、F10上，IICSO算法的平均值、标准差和最优值都是最好的。在函数F6上，IICSO算法的平均值是最好的，其最优值搜索到了函数F6的理论值。在函数F4上虽然ADSCSO算法的平均值和标准差都优于其他算法，但IICSO算法的最优值也搜索到了函数F4的理论值。在函数F5上，3种算法各有优势，其中CSO算法的标准差最优，ADSCSO算法的平均值最优，IICSO算法能够搜索到最优的最小值。在碗状函数F7上， IICSO算法的平均值、标准差和最优值都优于其他两种算法。在山谷状函数F8和陡峭形态函数F9上， IICSO算法的平均值和标准差明显比其他两种算法更有优势。综上所述，IICSO算法与其他两种算法相比，针对不同类型的测试函数具有更好的收敛性能和优化精度。

表3 CSO算法、ADSCSO算法和IICSO算法对比Tab.3 Comparisons of CSO、ADSCSO and IICSO algorithm

图3分别展示了CSO算法、ADSCSO算法和IICSO算法在10个不同测试函数下的适应值变化情况。为了清晰地比较3种算法，除测试函数F9外，其余测试函数适应值变化的纵轴采用对数处理后的数量级。从图3可以看出:对于测试函数 F1、F3、F8、F9、F10来说，IICSO算法的收敛速度和收敛精度都优于其他两种算法;对于测试函数 F6、F7来说，虽然IICSO算法前期收敛速度相对缓慢，但在中后期收敛速度加快，并且在收敛精度上也比其他两种算法有优势;对于测试函数F2、F4、F5来说，虽然IICSO算法的收敛速度不占优势，但在最优值搜寻中具有一定优势。从图3还可以看出，无论是针对高维还是低维搜索空间，无论是针对板状函数还是多局部极小值、碗状、山谷状测试函数，IICSO算法都能在全局搜索后以较快的收敛速度寻到较优解，优于ADSCSO算法和CSO算法，从而验证了IICSO算法在收敛速度和收敛精度方面的优势。

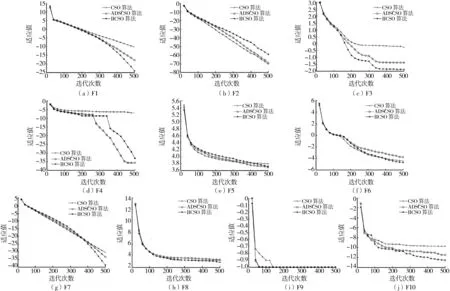
图3 适应值变化对比Fig.3 Comparisons of fitness change

3 结语

针对猫群优化算法两种行为模式猫群间缺乏交流而影响算法收敛速度和收敛精度的问题，本研究提出了一种基于两种行为模式猫群之间信息交互的猫群优化算法。该算法采用动态分组方案调整猫群的分组率，利用教与学优化算法的学习阶段实现不同猫群之间的交流学习。在10个测试函数上对CSO算法、ADSCSO算法和本研究的IICSO算法进行对比分析，发现两种行为模式猫群之间的信息交互提升了算法的全局搜索能力和收敛速度。