一种自行车停放装置的设计

郭家伟，王 佐，张宏强，顾柯悦

(马鞍山学院 大阪医工学院，安徽 马鞍山 243100)

自行车作为短途绿色出行的典型代表，正慢慢恢复其在交通体系中的地位，并改变着公共交通布局。国家统计局的数据表明，截至2019年底，我国两轮脚踏自行车产量达到4 978万辆[1]。自行车保有量的爆炸式增长也引发了一系列问题，例如随意占用城市、社区及校园的人行道。乱停乱放不仅抢占了公共资源，而且有碍交通，有损地区形象[2-3]。

与自行车停放相关的问题可以通过两种途径来解决。一是政策引导。政府施划停车空间，设置自行车停放引导员、运维员来规范停车行为。这些举措虽在一定程度上规范了自行车停放行为，但投入的人力物力较大[4-6]。二是开发有效的自行车停放装置。停放装置主要有横列插槽式、垂直悬挂式、空间多层式三种类型[7-9]。横列插槽式停放装置可将整排自行车前轮固定放置于插槽中，这种停放装置构造简单、安装方便，但会占用狭长的公共面积，空间利用率低，且单车间距较小，很容易倒成一片而剐蹭到行人和车辆，影响交通安全。空间多层式停放装置[10]采用抽拉的方式停放单车，用户按照存取程序将自行车推放到指定位置。这类装置自动化程度和空间利用率高，但成本也较高，且一般只有一个存取端口，易造成取放拥堵。垂直悬挂式停放装置[11]需要用户先将自行车停放至固定装置上，然后将固定装置垂直悬挂。此类装置操作简单，提高了空间利用率，但取放过程费时费力。综上，解决自行车停放问题需要综合考虑两个方面：一是需要充分利用地面；二是停放装置结构及操作简单，停取便利。

本研究在现有自行车停放装置的基础上，提出了一种由多组连杆机构组成的收拢式自行车停放装置。该装置结构简单，取放轻便，占地面积小，单次停放自行车数量多，可摆放于城市、社区及校园道路旁。

1 自行车停放装置结构设计

1.1 自行车形态物理模型

大多数自行车结构类似，只是尺寸略有差别。本研究以市场上占有率较高的某自行车品牌作为停放研究对象，建立了如图1所示的自行车形态物理模型。

图1 自行车形态物理模型Fig.1 The physical model of bicycle morphological

基于自行车形态物理模型，测量了该款自行车的形态特征值，测量结果见表1。将测量所得的形态特征值作为自行车停放装置功能尺寸计算的输入参数，以此完成整个装置的结构设计。

表1 自行车形态特征测量结果Tab.1 The measurement results of bicycle morphological characteristics

1.2 自行车停放装置结构

自行车停放装置如图2所示。该装置主要由圆盘、磁力锁及6组连杆机构组成，6组连杆机构均匀分布在圆盘上，圆盘可围绕自身轴线旋转。每组连杆机构均由前轮支架、后轮支架、气弹簧、承载连杆及摇杆构成，前轮支架及后轮支架安装在承载连杆两端，用于固定自行车前轮和后轮。摇杆一端通过铰链与承载连杆相连，另一端铰接在圆盘上。气弹簧一端通过铰链与摇杆相连，另一端铰链在圆盘上。每组摇杆上端配置有磁力锁头，可与圆盘圆周方向均匀分布的磁力锁座相配合。

图2 自行车停放装置Fig.2 The bicycle parking device

1.3 自行车停放装置工作原理

当用户需要停放自行车时，首先沿着圆盘径向拉动后轮支架，直至磁力锁头与磁力锁座吸合，此时承载连杆、摇杆及气弹簧贴合在圆盘表面，其状态如图2(a)所示；然后将自行车前轮及后轮固定在前轮支架和后轮支架上，完成自行车摆放；最后沿着圆盘轴向轻提后轮支架，直至磁力锁头与磁力锁座分离，此时气弹簧释放压力，摇杆在气弹簧的助力下摆动，推动承载连杆缓慢上升至指定位置，完成自行车停放，其状态如图2(b)所示。

2 自行车停放装置结构尺寸设计

自行车停放装置运动功能尺寸决定了用户能否顺利完成自行车取放，故本节主要将自行车形态特征值作为输入参数完成停放装置运动功能尺寸设计。

2.1 运动功能尺寸设计

自行车停放装置功能尺寸见图3。图3中：AO、DB及CE为承载连杆、摇杆和气弹簧初始时的位置；A1O1、DB1及C1E为承载连杆、摇杆和气弹簧终止时的位置；θ为承载连杆由初始位置AO旋转至终止位置A1O1时所转过的角度，且规定θ=60°；γ为摇杆DB和气弹簧CE的夹角，且为保证力传递的有效性，令γ=90°；h为后轮支架高度，且规定后轮支架高度h为后轮直径d的一半，即h=d/2=365 mm；L2为摇杆DB的长度。

图3 自行车停放装置功能尺寸Fig.3 The function size of the bicycle parking device

依据自行车形态特征测量结果可知：

L1=s+d/2，

(1)

式中：L1为承载连杆AO的长度；s为自行车前、后车轮转轴中心距。由式(1)计算可得L1=1 675 mm。

在直角△ADO中：

S2=L1·cosθ=837.5 mm，

(2)

式中：S2为摇杆DB1的长度。承载连杆由初始位置AO转动角度θ至终止位置A1O1，可得L2=S2=837.5 mm。

由此，可以计算出圆盘占地面积

(3)

在直角△CDE中结合运动关系可知：

(4)

式中：S3为铰点C与D之间的距离，且根据运动变换关系得L3=S3；a为气弹簧安装位置与圆盘边缘距离；S1为气弹簧伸展长度；l为气弹簧行程。由γ=90°及θ=60°可知∠CDE=60°。化简式(4)可得

2(S1-l)=837.5-a。

(5)

式(5)表示了气弹簧伸展长度S1、行程l及安装位置a之间的关系。查阅相关文献[12]，初选YQL023支撑型气弹簧，该型号气弹簧主要参数为S1=510 mm、l=210 mm及最小伸展力为130 N。将气弹簧参数代入式(5)计算可得S3=L3=300 mm、a=237.5 mm。

2.2 停放效能仿真实验

在不影响计算精度的情况下，运用ADAMS动力学仿真软件[13]建立了如图4所示的自行车停放装置仿真模型。图4中t为活塞杆顶部端点，θ为承载连杆转角，F为活塞杆受力。以气弹簧安装位置为坐标原点，在图4建立直角坐标系。设置各构件材料及质量属性，添加各构件间运动副，并在活塞杆处添加驱动力，进行动力学仿真实验。

图4 自行车停放装置仿真模型Fig.4 The simulation model of the bicycle parking device

活塞杆顶部端点t位移随转角θ变化曲线见图5。由图5可知，在转角θ=0°时t点与缸体底部距离为78 mm，当转角θ=60°时t点与缸体底部距离为285 mm，计算可得活塞杆行程为207 mm，与所选YQL023支撑型气弹簧理论行程基本一致，表明停放装置运动特性满足设计要求。

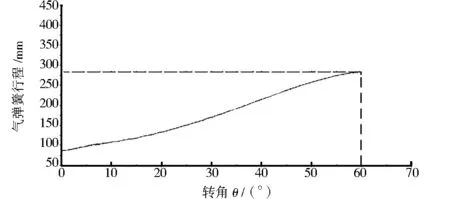
图5 活塞杆行程变化曲线Fig.5 The trip curve of piston rod

活塞杆受力F随转角θ变化曲线见图6。由图6可知，随着转角θ逐渐增至60°，活塞杆所受力F由15 N增至160 N，表明YQL023支撑型气弹簧伸展力满足活塞杆受力要求。由图6的曲线变化趋势还可知，转角θ逐渐增至45°后，活塞杆受力趋于平缓，有利于保持自行车在收拢停放过程中的稳定性。

图6 活塞杆受力变化曲线Fig.6 The force variation curve of piston rod

收拢停放过程中自行车质心角加速度随转角θ变化曲线见图7。由图7可知，随着转角θ由0°逐渐增至60°，自行车质心角加速度最大值为0.14 r/s2，表明自行车在收拢停放过程中稳定性较好。

图7 自行车质心角加速度变化曲线Fig.7 The variation curve of angular acceleration of bicycle centroid

3 结论

(1)本研究所设计的可收拢式停放装置可以实现自行车停放，结构简单，操作方便，在占地面积为2.2 m2的情况下，可以完成多辆自行车停放。

(2)在收拢停放过程中，自行车质心处最大角加速度为0.14 r/s2，表明停放过程中自行车稳定性较好。