RC框架结构倒塌地震易损性评估

郑山锁，温桂峰，董立国，杨威，刘巍，张艺欣

(1. 西安建筑科技大学 土木工程学院；结构工程与抗震教育部重点实验室，西安 710055；2. 广州容柏生建筑结构设计事务所(普通合伙)上海分所，上海 200063；3. 同圆设计集团有限公司，济南 250101)

21世纪初，苏门答腊地震后，全球进入了地震高发期，中国作为典型的地震多发国家，同样进入了新的地震活跃期，这为中国防震减灾工作带来了严峻考验。据统计，2008年汶川地震中死亡人数超过6.94万，受伤人数超过37.4万；2013年玉树地震中，死亡人数超过2 600，受伤人数达到9 000多。房屋建筑的倒塌破坏是造成震时人员伤亡的主要原因，因此，控制和预测建筑结构在地震作用下的倒塌是当前防灾减灾工作的重中之重。

结构倒塌易损性分析方法作为结构性能化抗震理念的重要组成部分，近年来逐步发展成为评估结构抗倒塌能力的主流方法。2009年，美国应用技术委员会(ATC)颁布了第一部结构抗倒塌性能评估标准FEMA P695[1]，建立了基于IDA分析的结构倒塌易损性分析方法。此后，基于该分析方法，Elshear等[2]、钱凯等[3]、Huang等[4]分别对某一RC框架结构进行了抗地震倒塌性能数值模拟分析；Lu等[5]研究了构件尺寸及配筋对RC框架结构抗倒塌能力的影响；苏佶智等[6]讨论了轴压比、梁柱线刚度比变化对RC框架结构抗倒塌能力的影响；罗开海等[7-9]对不同设防烈度和不同层数RC框架结构的抗倒塌能力进行了研究；邓颖婷[10]对不同跨度和不同层数的RC框架结构的抗倒塌能力进行了数值模拟；范萍萍等[11]讨论了不同设防烈度和抗震等级对RC框架结构抗倒塌能力的影响；周洲等[12]对中国近年来关于建筑结构地震倒塌易损性方面的研究成果进行了整理和分析，发现现阶段中国建筑结构的倒塌风险尚不具有一致性。综合上述研究结果可以看出，目前学者们虽然已经对建筑结构的抗地震倒塌能力开展了大量研究，但其研究主要集中于探讨某一设计参数对结构抗倒塌性能的影响，缺乏对一类建筑结构抗倒塌性能的系统性评价，不利于从整体角度科学认识一类建筑结构的抗倒塌性能。

鉴于此，笔者以符合中国现行设计规范的RC框架结构为研究对象，考虑设防烈度、结构层数及跨度变化对抗地震倒塌能力的影响，设计了66个典型RC框架结构，基于IDA分析方法，分别对其进行抗倒塌性能评估，并剖析了该类结构抗倒塌能力的概率分布，以期为总体认识中国RC框架的抗倒塌性能提供参考。

1 典型结构的设计

结构设计参数的离散性和所处场地的多样性是研究结构抗地震倒塌能力时不可忽视的两个重要因素。ATC-63[13]提出可通过引入体现某一类抗侧力体系主要倒塌特征的代表结构，即典型结构来解决结构设计参数的离散性问题。Haselton等[14]指出，典型结构消除了单个建筑物和一类群体结构抗震性能预测间的隔阂。因此，为了研究依中国规范设计的RC框架结构的抗地震倒塌能力，笔者基于ATC-63[13]和Syner-G[15]中关于典型结构的建立方法，结合中国现行设计规范，并综合考虑设防烈度、建筑高度和跨度3种因素对结构倒塌性能的影响，建立了66个不同设计参数的典型RC框架结构，各典型结构的层数、跨度、设防烈度分布如图1所示。

图1 典型结构逐层细化示意图Fig.1 Layer by layer detailed schematic diagram

针对各典型结构，依据中国现行设计规范，以弹性层间位移角限值为目标，通过反复迭代设计得到各典型结构中构件的几何尺寸与详细配筋。为使设计的结构具有典型性，按照如下规则确定结构设计参数及梁柱构件的几何尺寸：

1)梁截面尺寸：认为每层梁的截面不变，但不同层数梁的截面有所不同，基于规范规定，并满足工程模数要求及最少截面类型要求，将梁宽取为250 mm，梁高取梁跨的1/10～1/18，同时，考虑到梁截面的实际配筋和施工情况，部分梁的截面宽度可由250 mm增至300、350、400 mm。

2)柱截面尺寸：对于不超过10层的结构，其框架柱应符合规范规定的最小截面尺寸要求，并尽量减少截面类型。

3)结构荷载信息：对于楼面和屋面荷载，参考文献[16-17]中恒载的简化取值方法，对楼板、装修、隔墙、外墙等恒载均折算为楼板恒载输入，折算后的楼面及屋面恒载取为8 kN/m2、活载取为2 kN/m2，并考虑周期和楼面活荷载折减；结构的设计地震分组为第二组，场地类别为Ⅱ类；基本风压为0.4 kN/m2、地面粗糙度为C类，基本雪压为0.3 kN/m2。

4)构件设计信息：梁、柱纵筋采用HRB400钢筋；箍筋采用HPB300钢筋；2层、5层结构的混凝土强度等级采用C30；8层、10层混凝土强度等级采用C40；楼面及屋面板厚分别取120 mm(跨度6 m和8 m)和100 mm(跨度4 m)；梁、柱构件的保护层厚度取20 mm，板保护层厚度取15 mm。其详细配筋信息见文献[18]。

基于上述设计信息，采用PKPM软件设计了各典型RC框架结构。其中，不同层数6 m跨度典型RC框架结构的PKPM模型如图2所示。

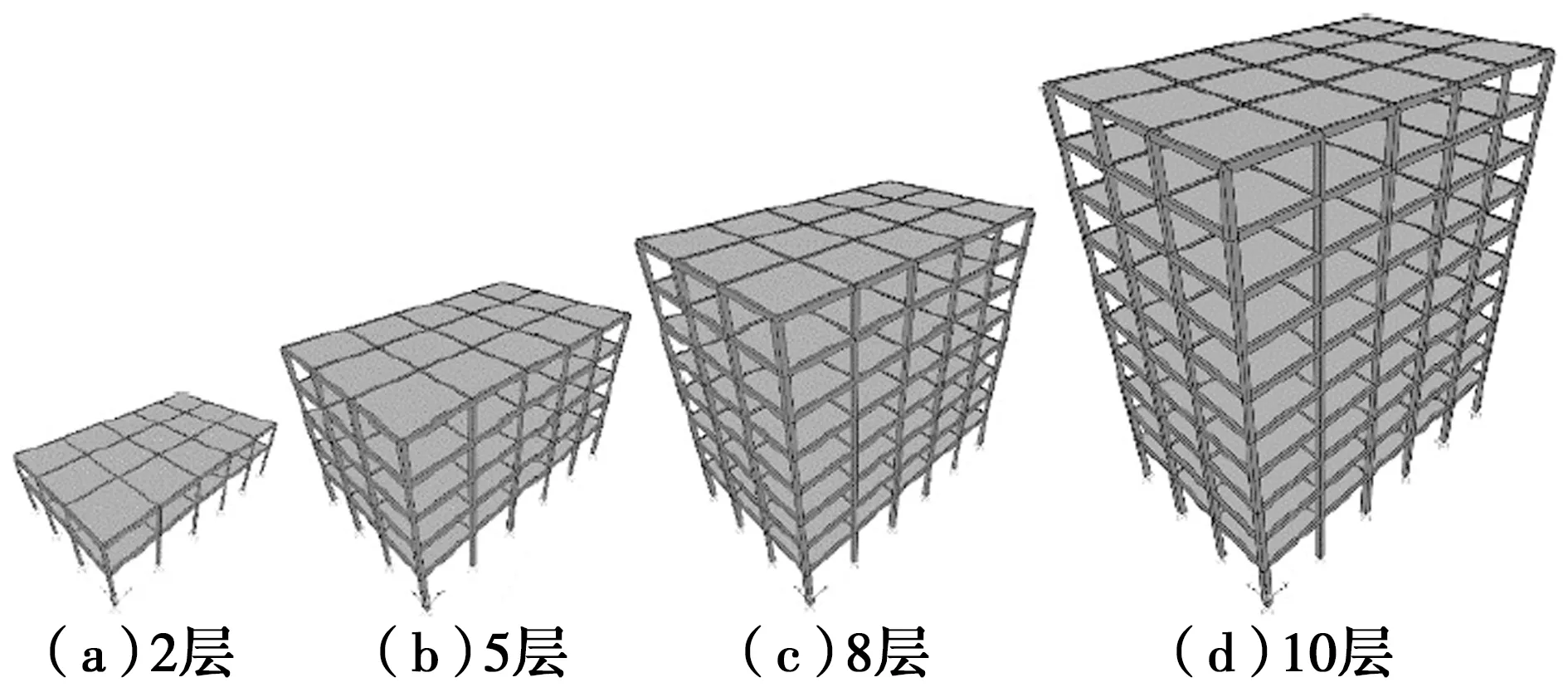
图2 6 m跨度典型RC框架结构PKPM模型Fig.2 PKPM model of 6 m span typical RC frame

2 RC框架结构塑性铰模型的建立

目前，针对RC框架结构的数值模拟方法主要有基于材料本构关系的纤维模型与实体元模型，以及基于截面弯矩-转角关系的集中塑性铰模型。考虑到结构倒塌易损性分析通常以大量IDA分析为基础，而基于材料本构关系的纤维模型和实体元模型在强非线性条件下计算耗时巨大的现状，以及在地震作用下RC框架结构构件一般在梁、柱构件端部形成塑性铰，发生破坏，而构件中部通常保持弹性的特性，采用基于集中塑性铰模型的RC框架结构的数值建模方法。相对纤维模型和实体元模型，集中塑性铰模型仅需确定构件端部非线性弹簧单元的力与变形关系就可以较准确地模拟构件的非线性行为，且能够在保证精度的同时大大降低数值计算成本。鉴于此，基于OpenSEEs平台建立考虑节点剪切变形的RC框架结构集中塑性铰模型(如图3所示)，并对该结构模型进行倒塌分析。

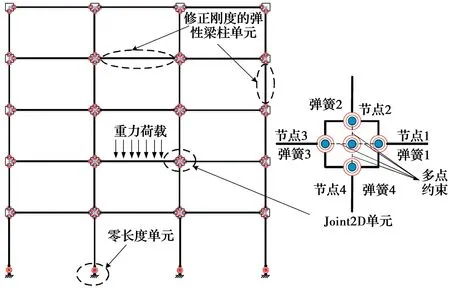
图3 考虑节点剪切变形的RC框架结构的塑性铰模型Fig.3 Plastic hinge model of RC frame structure considering joint shear

2.1 RC框架梁、柱构件数值模型

RC框架结构集中塑性铰模型将框架梁柱单元简化为弹性杆单元和端部零长度塑性铰单元的串联体系，准确建立梁柱单元集中塑性铰模型的关键是确定中部弹性杆单元和端部塑性铰单元的力学性能参数。

2.1.1 中部弹性杆单元 由于力学模型的简化，采用一般的弹性梁柱单元对梁柱集中塑性铰模型中部的弹性杆进行模拟时，所得到的梁柱塑性铰模型的刚度将与构件的实际刚度不符，从而导致结构动力特性产生较大误差，得出错误的结构地震反应分析结果。Zareian等[19]针对这一问题，提出了保证集中塑性铰具有正确刚度的修正方法，该方法通过修正内部弹性单元的截面惯性矩、单元刚度系数和端部塑性铰单元的刚度予以实现。采用Zareian等[19]建议的修正方法，对梁柱单元集中塑性铰模型的相关参数进行修正，具体修正方法为

(1)

(2)

(3)

(4)

式中：Ec为弹性模量；I为构件的截面惯性矩；L为构件长度；Ks为弹簧单元初始刚度；Ie为修正后内部弹性单元(ModElasticBeam2d)的截面惯性矩；Sii、Sjj、Sij、Sji为修正后内部弹性单元的刚度系数；n=Ks/Ke，Ke(Ke=6EIe/L)为内部弹性单元的转动刚度。在保证集中塑性铰模型转动刚度与实际单元刚度相等的前提下，对于修正刚度的弹性单元(ModElasticBeam2d)，当n取值越大，该单元的刚度矩阵与一般弹性杆单元的刚度矩阵越接近，但较大的n值容易造成数值计算不收敛，参考Zareian等[19]的建议，取n=10。

2.1.2 塑性铰单元 强烈地震作用下，RC框架结构中梁、柱构件端部塑性铰区的弯矩-转角关系通常具有峰值指向性特点，因此，采用Ligons等[20]提出的具有峰值指向性特点的滞回模型ModIMKPeakOriented描述梁柱塑性铰区的弯矩-转角关系，如图4所示。该滞回模型的骨架曲线由6个参数控制，即初始刚度Ks、屈服弯矩My、强化系数αs,s、塑性转角θcap,pl、峰值后转角θpc和循环能量耗散能力λ。其中，弹簧单元的初始刚度Ks按式(1)计算确定；对于其余参数的取值，Haselton等[21]基于255个柱试验数据建立了相应的预测公式并验证了公式的准确性，笔者采用该预测公式确定塑性铰单元的力学性能参数。各参数的具体预测公式如表1所示。

表1 塑性铰单元恢复力模型各参数计算式

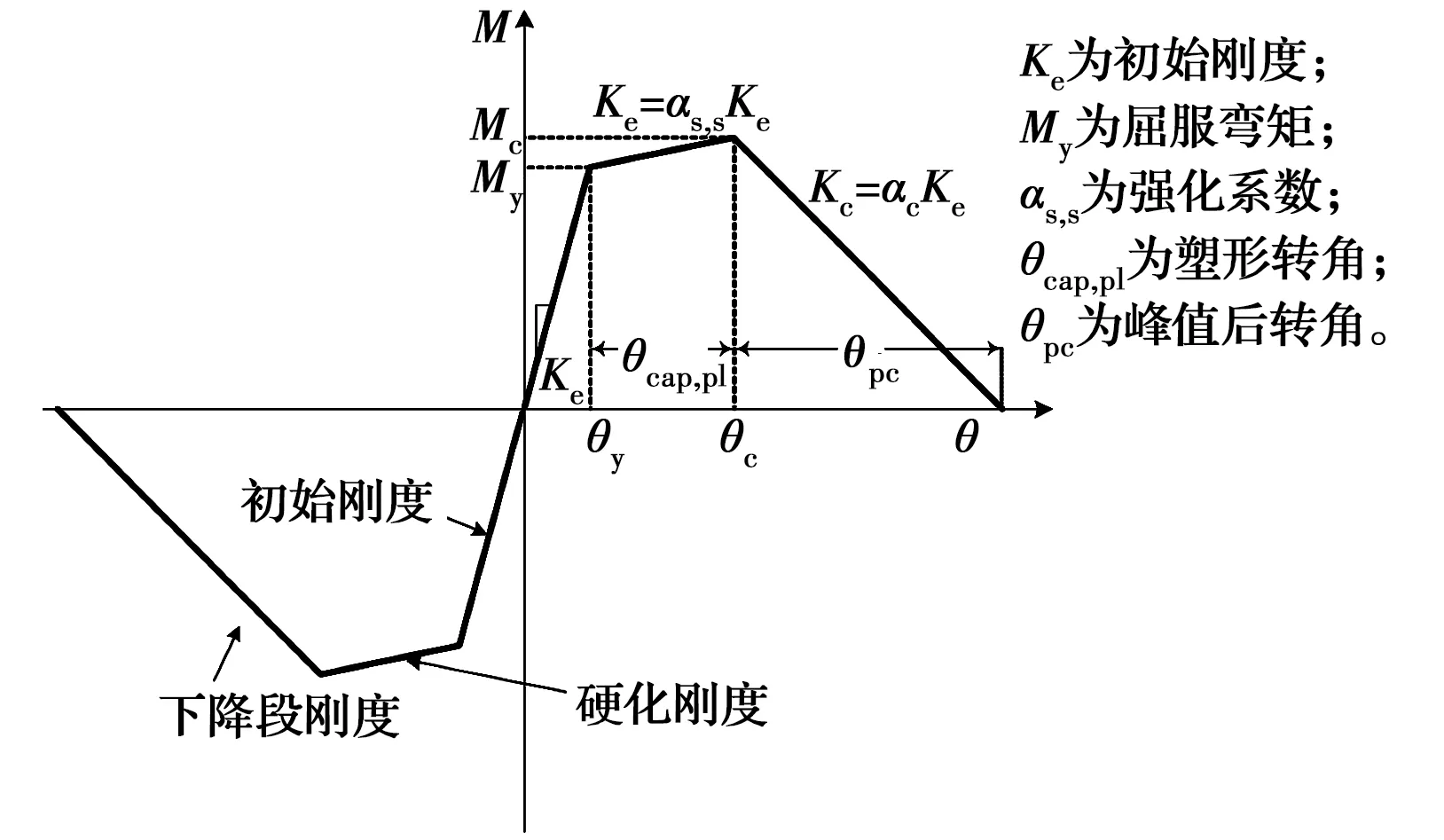
图4 塑性铰单元模型Fig.4 Plastic hinge element

此外，由于集中塑性铰模型同样采用瑞利阻尼，且仅考虑内部弹性单元的刚度阻尼，不考虑弹簧单元的刚度阻尼，而已对内部弹性单元的刚度进行了修正，因此，为得到正确的刚度阻尼，应对内部弹性单元的刚度阻尼系数进行修正。

(5)

式中：β为刚度阻尼系数；β′为修正后的刚度阻尼系数。

2.2 RC框架梁柱节点域数值模型

严格依据中国现行规范设计的RC框架结构均满足“强节点弱构件”的抗震设计原则，数值模拟分析中通常将节点作为弹性或刚性节点，即不考虑节点破坏。然而，历次震害资料表明，节点剪切破坏亦是RC框架结构的典型震害，且其破坏易引发RC框架结构倒塌。鉴于此，为有效考虑节点剪切破坏对RC框架结构抗地震倒塌能力的影响，采用Altoontash等[22]提出的二维梁柱节点单元(element Jiont2d)模拟节点剪切变形，建立了考虑节点剪切变形的RC框架结构集中塑性铰模型，如图3所示。

Jiont2d节点单元包含4个位于梁柱构件与节点交界面处的转角弹簧和1个位于节点中心的转动弹簧，其中，4个转角弹簧用以模拟梁柱端的转动变形，中心转动弹簧用以模拟节点的剪切变形。采用Hysteretic滞回模型模拟节点域剪切恢复力特性，其中，剪切恢复力模型的开裂点、屈服点、峰值点的剪应力和剪应变采用Teraoka等[23]模型计算确定，并根据式(6)转换为相应的弯矩-转角关系；对于节点域剪切块的滞回特征取值，参考Altoontash[22]建议的参数值，捏缩点的应力值取为最大历史应力的25%，应变值取为最大历史转角的25%。

(6)

式中：Mi、θi为不同受力状态下节点中心转动弹簧的弯矩和转角；τi、γi为节点各受力状态下的剪应力和剪应变，计算公式见文献[22]；hc为柱截面高度；bj、hj为节点核心区的有效宽度和截面高度；Lc为上下柱的总高度；db为梁截面高度；Lb为左右梁的总长度；j为内力矩系数，通常取0.875。

2.3 RC框架结构塑性铰数值模型的试验验证

为验证上述集中塑性铰模型建模方法的准确性与合理性，以清华大学完成的缩尺比例为1∶2的3层RC整体框架拟静力倒塌试验[24]为参照，根据物理试验中的构件尺寸、配筋信息及材料的力学性能等参数，按照前述建模方法，确定各梁柱单元的集中塑性铰模型和节点域剪切模型，按图3建立该试验模型的集中塑性铰数值模型，并进行模拟加载，得到其模拟滞回曲线，进而与试验结果进行对比，如图5所示。

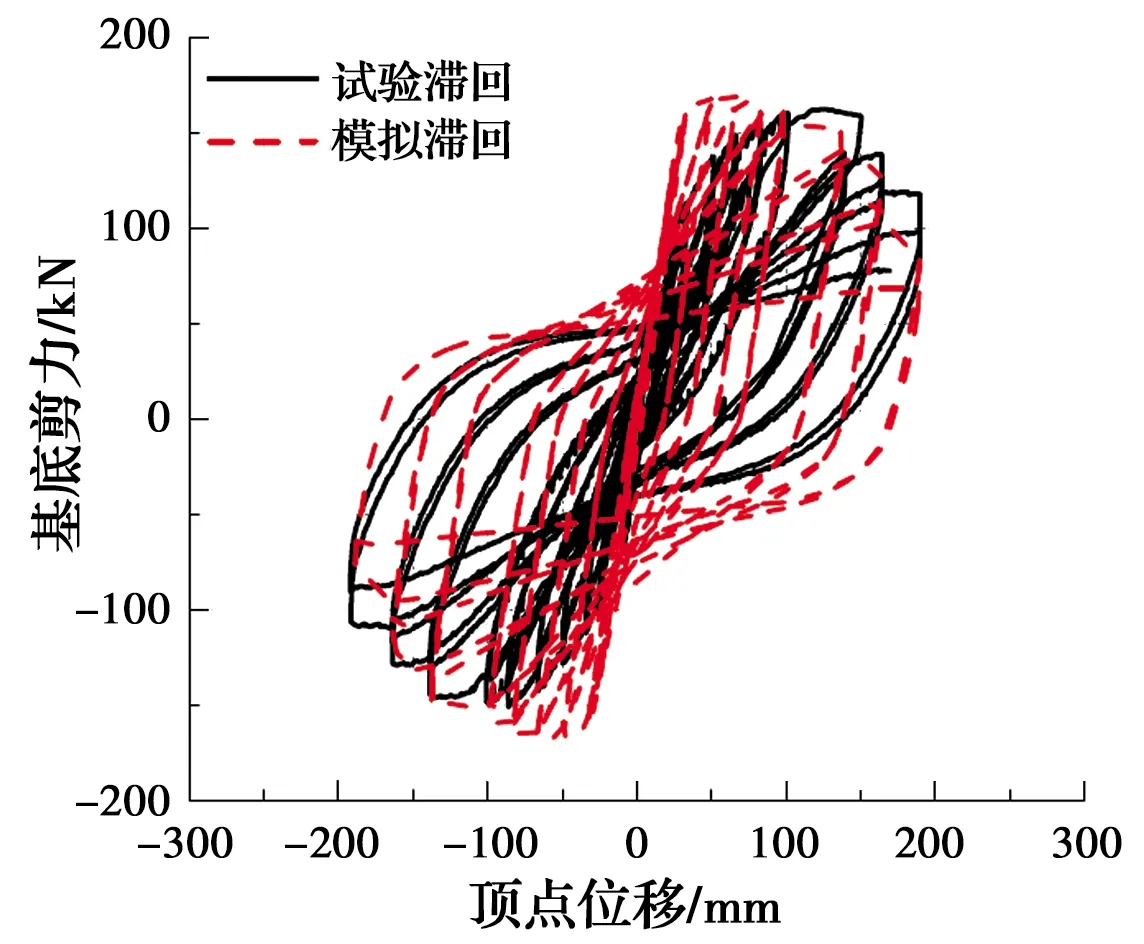
图5 试验与模拟滞回曲线对比Fig.5 Comparison of experimental and simulated

由图5可看出，在模拟得到的在滞回曲线下降段，即结构接近倒塌阶段时，与试验结果的吻合程度较好。模拟滞回曲线也较好地反映了结构近倒塌状态的强度退化特性，表明基于集中塑性铰模型的数值建模方法对RC框架结构的倒塌模拟具有良好的适用性，可用于该类结构的抗倒塌性能分析。

3 RC框架结构倒塌易损性分析

3.1 倒塌点定义与IDA曲线

采用前述数值建模方法，分别建立66个典型结构的集中塑性铰模型，并以ATC-63[13]中推荐的22条远场地震动作为输入地震动记录，分别对各典型结构进行IDA分析，直至引起结构倒塌。其中，每次IDA分析实际上是一次一致激励(uniform excitation)模式下的动力时程分析。

地震荷载作用下，RC框架结构的倒塌行为本质上是一种动力失稳问题，即在微小的地震强度增量下，结构的动力响应将急剧增大。基于此，将地震动强度的微小增量，即引发结构动力响应发生显著变化的动力失稳点定义为结构的倒塌点[18]，其在IDA曲线上表现为曲线变平的拐点。IDA分析过程中，为了准确捕捉结构的倒塌特征点，并减少地震动调幅次数，借鉴Vamvatsikos等[25]提出的hunt & fill算法对输入地震动强度进行调幅。既有研究结果表明[16]，采用结构一阶周期谱加速度Sa(T1)作为地震动强度指标，可有效降低易损性分析中的不确定性，且考虑到最大层间位移角响应θmax与RC框架结构的震损破坏程度具有显著的相关性，因此，采用一阶周期谱加速度Sa(T1)作为地震动强度指标，采用最大层间位移角响应θmax作为工程需求参数，绘制各典型结构的IDA曲线。以5层、6 m跨度的典型RC框架结构F-5-6m为例，给出其6、7、8度设防设计的典型RC框架结构的IDA曲线及其倒塌特征点识别结果，如图6所示。

由图6可看出，最上面一条IDA曲线的数值明显高于其他曲线，其原因为：以图6(c)为例，IDA分析时，首先需要对所选地震波进行调幅，使其在结构自振周期T1=0.875时的Sa(T1)相等，以Sa(T1)=2.0g为例，给出调幅后输入的地震动谱加速度曲线，如图7所示，图中各曲线与Y轴的交点为输入地震动的峰值加速度PGA。由图7可知，相同的Sa(T1)下，存在一条地震动记录的PGA明显小于其他地震动记录的PGA，因此，对于该地震动记录，需要调幅到更大的Sa(T1)，才能使结构发生倒塌破坏，这是图6(c)中最上面一条IDA曲线的数值明显高于其他曲线的主要原因。该曲线对应的输入地震动记录也是结构可能遭遇的地震动，因此，在后续的概率分析中应该包含这一结果，以反映频谱特性差异性对结构抗倒塌能力的影响。

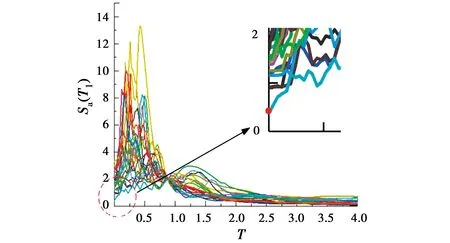
图7 调幅后的地震动谱加速度曲线Fig.7 Seismic spectrum acceleration curve

3.2 倒塌储备系数CMR及相关性分析

图6中各倒塌特征点的纵坐标实际上反映了结构的抗倒塌能力。由于地震动动力特性的差异，结构的抗倒塌能力具有明显的不确定性，为合理量化结构的抗倒塌能力，FEMA P695[1]建议采用倒塌储备系数CMR表征结构的抗倒塌能力。CMR反映了结构实际抗倒塌能力与设防需求间的量化关系，其值越大，表明结构的抗倒塌储备越高，即结构的抗倒塌能力越强。当以一阶周期谱加速度作为地震强度指标时，倒塌储备系数CMR可按式(7)计算。

(7)

式中：Sa(T1)50%为有50%地震波输入结构模型使其发生倒塌时对应的地震动强度；Sa(T1)大震为规范建议的罕遇地震下的地震动强度，可按式(8)计算。

Sa(T1)大震=a(T1)大震g

(8)

式中：a(T1)大震为结构基本周期为T1时所对应的罕遇地震下的水平地震影响系数，可按中国现行抗震设计规范所述方法计算确定；g为重力加速度。

根据式(7)～式(8)以及各典型结构的IDA曲线，计算得到66个典型RC框架结构的倒塌储备系数CMR，并以此作为RC框架结构倒塌储备系数的样本，对其进行统计分析。结果表明，所有典型RC框架结构的CMR均在1.82～7.09范围内，其均值和中位数分别为3.37和3.16，置信度为95%的置信区间为[3.09，3.65]。根据66个典型结构的倒塌储备系数CMR的分析结果，给出其频数分布和累计概率分布结果，如图8所示。

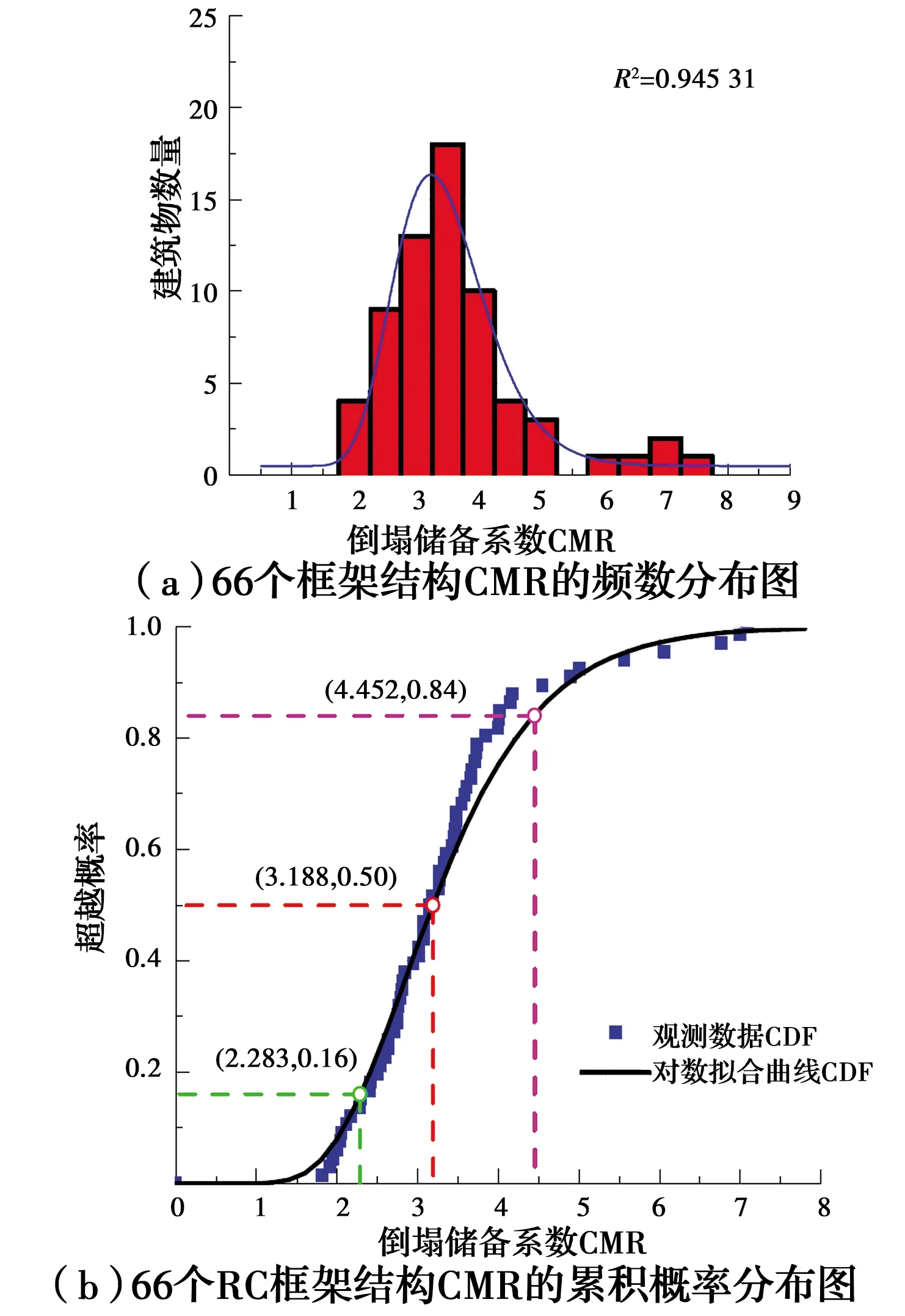
图8 66个RC框架结构CMR的频数及累积概率分布图Fig.8 Frequency and cumulative probability distribution chartof 66 RC frame structures’

由图8可以看出，当采用对数正态分布函数对典型RC框架结构的倒塌储备系数CMR进行参数拟合时，其拟合优度R2大于0.94，表明按中国现行规范设计的RC框架的倒塌储备系数概率分布基本服从对数正态分布，同时，根据统计分析结果，求出典型RC框架结构倒塌储备系数CMR概率分布的中位值及对数标准差分别为3.188和0.332，16%及84%分位点为2.283和4.452。该结果符合中国RC框架结构抗倒塌能力储备情况，可作为初步评估符合中国现行规范的RC框架结构抗地震倒塌能力的依据。

对各典型结构的倒塌储备系数CMR进行统计分析，得到其与结构设计参数的相关性矩阵，如表2所示。由表2可以看出，CMR和设防烈度间的相关系数为-0.308，与层数间的相关系数为-0.373，即随着设防烈度和层数的增大，CMR呈下降趋势；而CMR和跨度的相关性较弱，但两者仍是负相关，即CMR随着跨度的增大而减小。

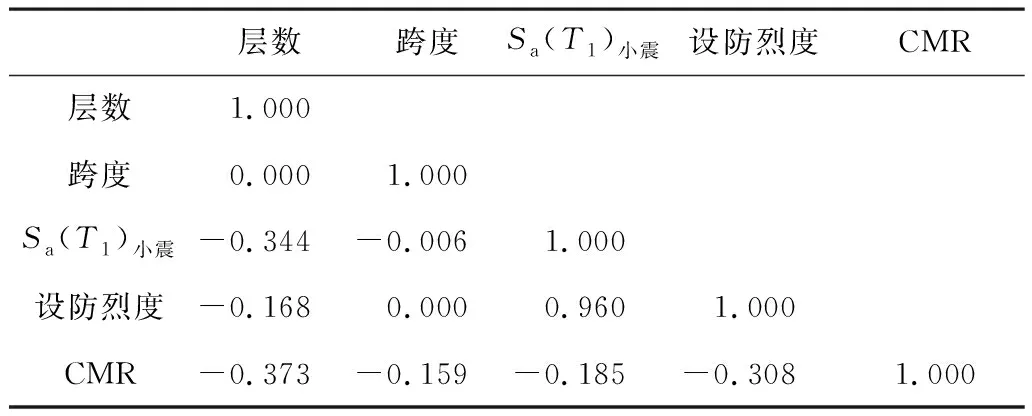
表2 CMR与结构设计参数间相关性系数矩阵

表2中的相关性分析总体上反映了RC框架结构的倒塌储备系数CMR随设防烈度、跨度以及层数的变化关系。然而，由于设防烈度、跨度和层数的不同，其CMR变化关系还具有一定的差异性。

不同层数、相同跨度RC框架结构的CMR随设防烈度的变化关系如图9所示。由图9可以看出，对于跨度为4 m的RC框架结构，2层和5层结构的CMR在8度设防时最小，8层与10层结构的CMR在7度设防时最小；对于跨度为6 m的RC框架结构，各层数结构的CMR均在7.5度设防时最小；对于跨度为8 m的RC框架结构，2层和5层结构的CMR在8度设防时达到最小，8层和10层结构的CMR在7.5度设防达到最小；将不同跨度下结构的CMR取平均值，可以发现各层数结构的CMR平均值在7.5度设防时达到最小值，即依据中国现行规范设计的7.5度设防RC框架结构的抗倒塌能力最弱。

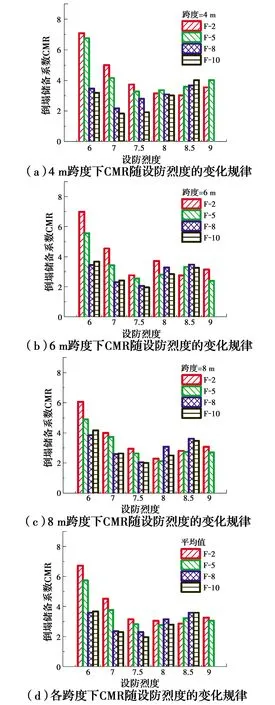
图9 同一跨度下CMR随设防烈度的变化规律Fig.9 Variation law of CMR under the same span with the change of fortification

不同跨度、相同设防烈度RC框架结构的CMR随层数的变化关系如图10所示。由图10可以看出，当设防烈度小于7.5度时，RC框架结构的CMR值随层数增大不断降低，且其下降速率随着设防烈度的提高不断减缓；当结构的设防烈度达到8度时，其CMR开始随层数增大而趋于稳定，其值约为3；设防烈度达到8.5度时，RC框架结构的CMR随着层数的增大而略有提升，其值在3～4的区间内变化；设防烈度为9度时，CMR随层数增加而保持恒定，其值约为3。

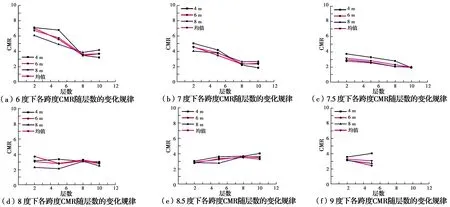
图10 同一烈度下各跨度CMR随层数的变化规律Fig.10 CMR’s variation law with the change of story number under the same

产生该现象的原因为[18]：设防烈度较低的RC框架结构设计水平地震力相对较小，对于层数较少的结构，其配筋一般为构造配筋，因而结构实际抗震性能相对理论计算值具有较大富余，但层数较多的结构，其配筋几乎取决于理论计算结果，因此，低设防烈度下RC框架结构的CMR随着层数的增加不断减小，抗倒塌能力不断降低。当设防烈度增大时，不同层数RC框架结构的配筋均由设计水平地震力控制，其抗倒塌能力的冗余性相当，因此，随着层数的增多，结构的CMR系数基本不变且略有增大，说明所设计的典型结构具有较一致的地震倒塌风险。

3.3 倒塌易损性分析

倒塌易损性描述了给定地震强度下结构的倒塌概率，由于结构的倒塌行为本质上是一种动力失稳问题，因此，通常采用基于强度易损性的函数形式构建结构的倒塌易损性模型，具体做法为[26]：根据图6分析得到的结构倒塌点，采用式(9)所示的频数统计方法，获取结构在不同强度地震作用下的倒塌概率，进而采用式(10)对获取的倒塌概率进行参数拟合，得到连续的倒塌易损性曲线，其分析示意如图11所示。

(9)

(10)

式中：NC为NR条地震动记录中使结构倒塌的地震动记录数量；mR为结构抗倒塌能力的中位值；βR为结构抗倒塌能力对数标准差，当仅考虑地震动的RTR不确定性时，βR=βRTR；Φ为标准正态概率分布函数。然而，基于集中塑性铰模型对RC框架结构进行倒塌易损性分析时，还应考虑建模不确定性对βR的影响。Haselton[14]通过分析集中塑性铰模型中对倒塌预测有影响的各个参数，给出建模不确定性参数βM，建议取值为0.5。

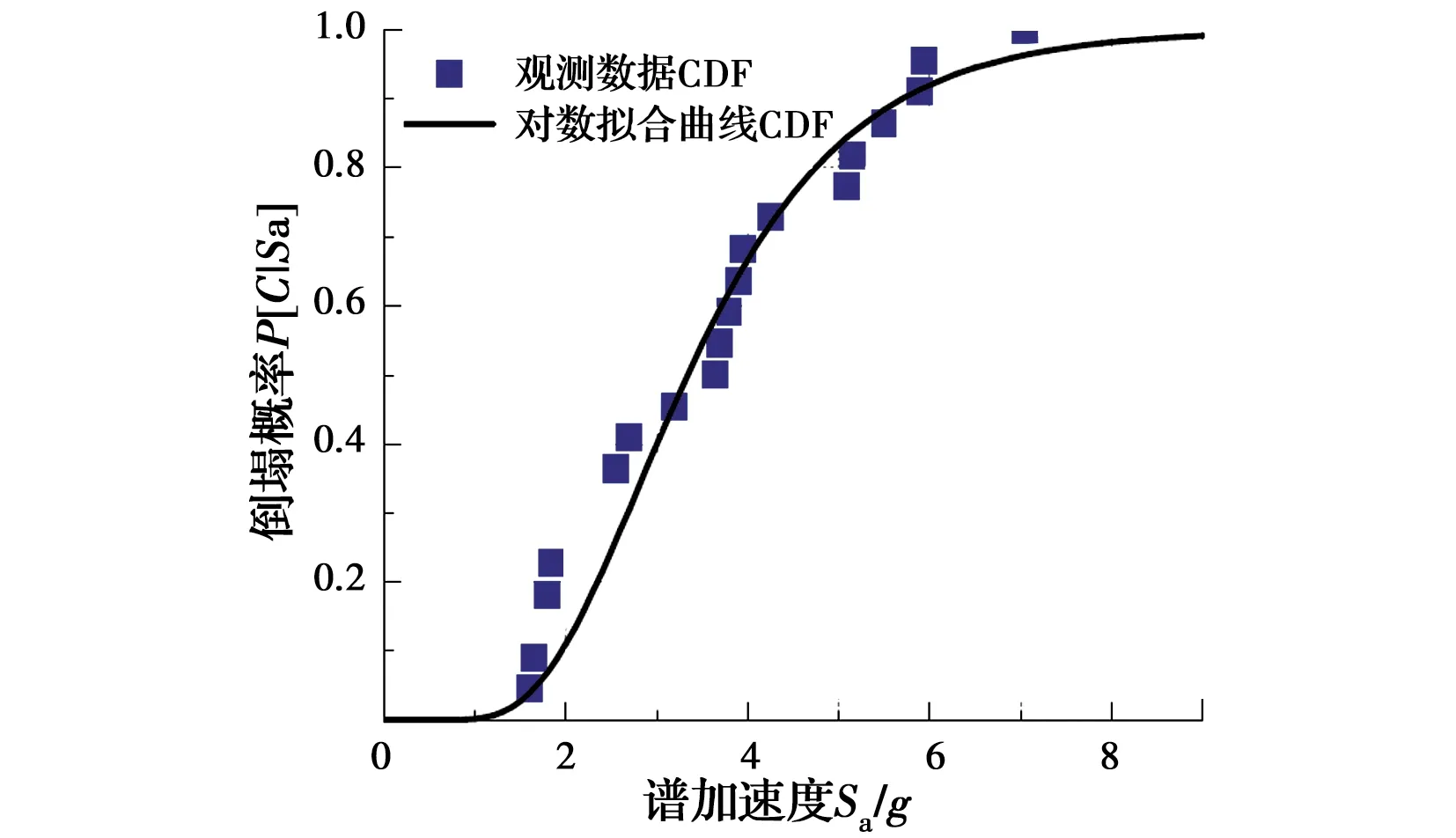
图11 倒塌易损性曲线的拟合Fig.11 Fitting of collapse vulnerability

鉴于建模不确定性对结构抗倒塌能力的中位值并无影响，根据式(10)拟合得到各典型RC框架结构抗倒塌能力的中位值mR和仅考虑地震动RTR不确定性的βRTR后，进一步取βM为0.5，按式(11)计算得到其相应的抗倒塌能力对数标准差βR，并带入式(10)，得到各典型RC框架结构的倒塌易损性曲线，其横坐标归一化处理，即除以相应大震下的谱加速度Sa(T1)大震后的结果见图12。

图12 同一设防烈度不同跨度与层数RC框架结构倒塌易损性曲线Fig.12 RC frame structure’s collapse fragility curves under the different span and story number and the same fortification

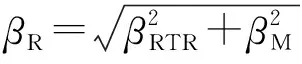
(11)

式中：βRTR值为各结构抗倒塌能力的对数标准差。

3.3.1 大震下结构倒塌概率分析 依据上述倒塌易损性分析结果，计算得到各典型RC框架结构在大震下的倒塌概率结果，见表3，并作出大震倒塌概率的频数及累积概率分布图，如图13所示。由表3和图13可以看出，按中国现行规范设计的典型RC框架结构在大震作用下的倒塌概率分布于[0.1%，16.7%]区间内，其中，84.8%的结构倒塌概率小于10%，15.2%的结构倒塌概率在10%～16.7%范围内。设防烈度为7.5度和8度的8层、10层结构是倒塌概率在10%以上的RC框架结构的主要群体。相应层数和设防烈度的各跨度典型结构的大震倒塌率平均值列于表3。由表3可以看出，F-8-7度、F-10-7度的倒塌概率较一致，约为10%，而F-8-7.5度、F-10-7.5度的倒塌概率超过了10%，其余结构的倒塌概率在8%以下。ATC-63报告[13]建议以设防大震下结构倒塌概率不超过10%作为结构达到大震不倒性能要求的标准，由此可以说明，依据中国现行规范设计的RC框架结构具有91%的可靠度，满足大震不倒的设防目标。

3.3.2 特大震下结构倒塌概率分析 建筑结构在

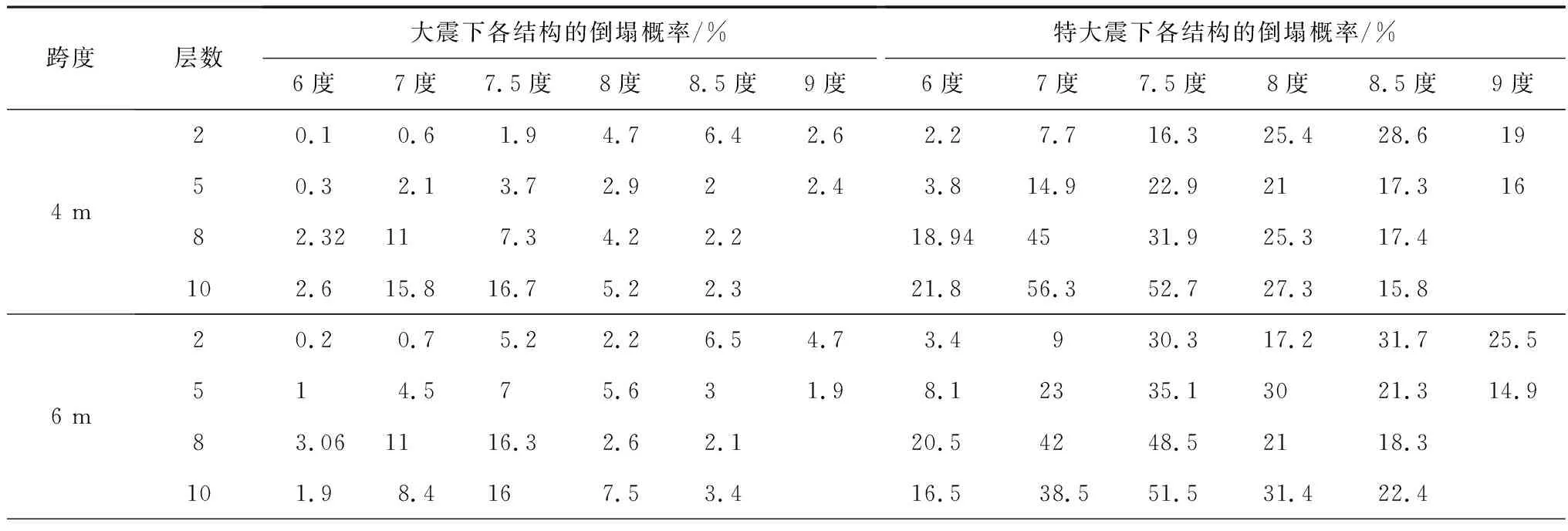
表3 各跨度RC框架的倒塌概率

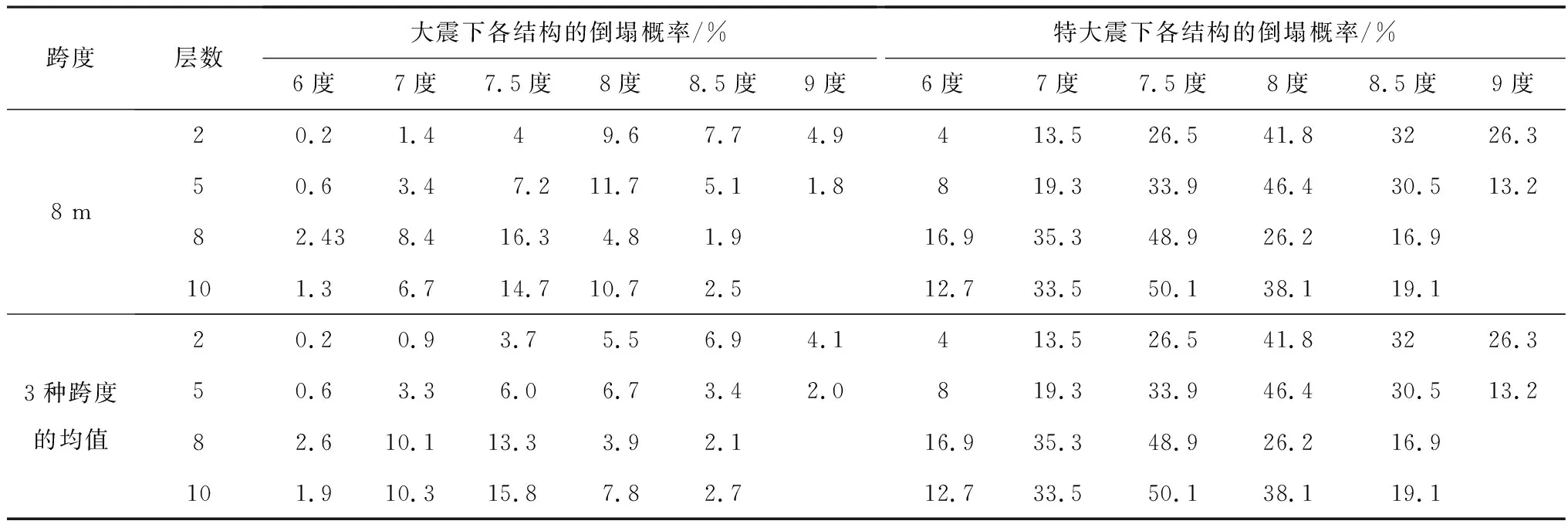
续表3

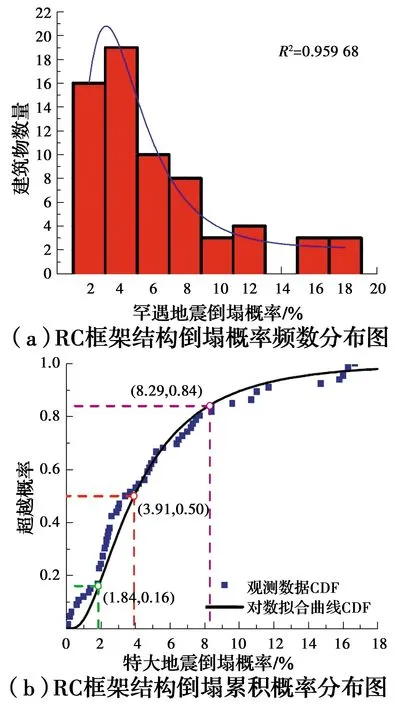
图13 各RC框架结构倒塌概率频数及累积概率分布图Fig.13 Collapse frequency and cumulative probability distribution chart of each RC frame

服役年限内可能遭遇超越罕遇地震烈度水平的特大地震，从而带来巨大的经济损失和人员伤亡，如2008年汶川地震中，震中大范围区域遭遇了大于设防烈度标准的特大地震，因此，汶川地震后，中国部分学者提出[27]应该总结和反思上述地震灾害的经验和教训，在中国的建筑防震设防体系中考虑特大地震的影响。

为明确按中国规范设计的RC框架结构在特大地震作用下的抗倒塌性能，参考文献[28]，取特大地震的地震强度Sa(T1)特大震=2Sa(T1)大震，计算各典型RC框架结构在特大地震作用下的倒塌概率，见表3，并以此为统计分析对象，作出其特大震倒塌概率的频数分布及累积概率分布图，如图14所示。

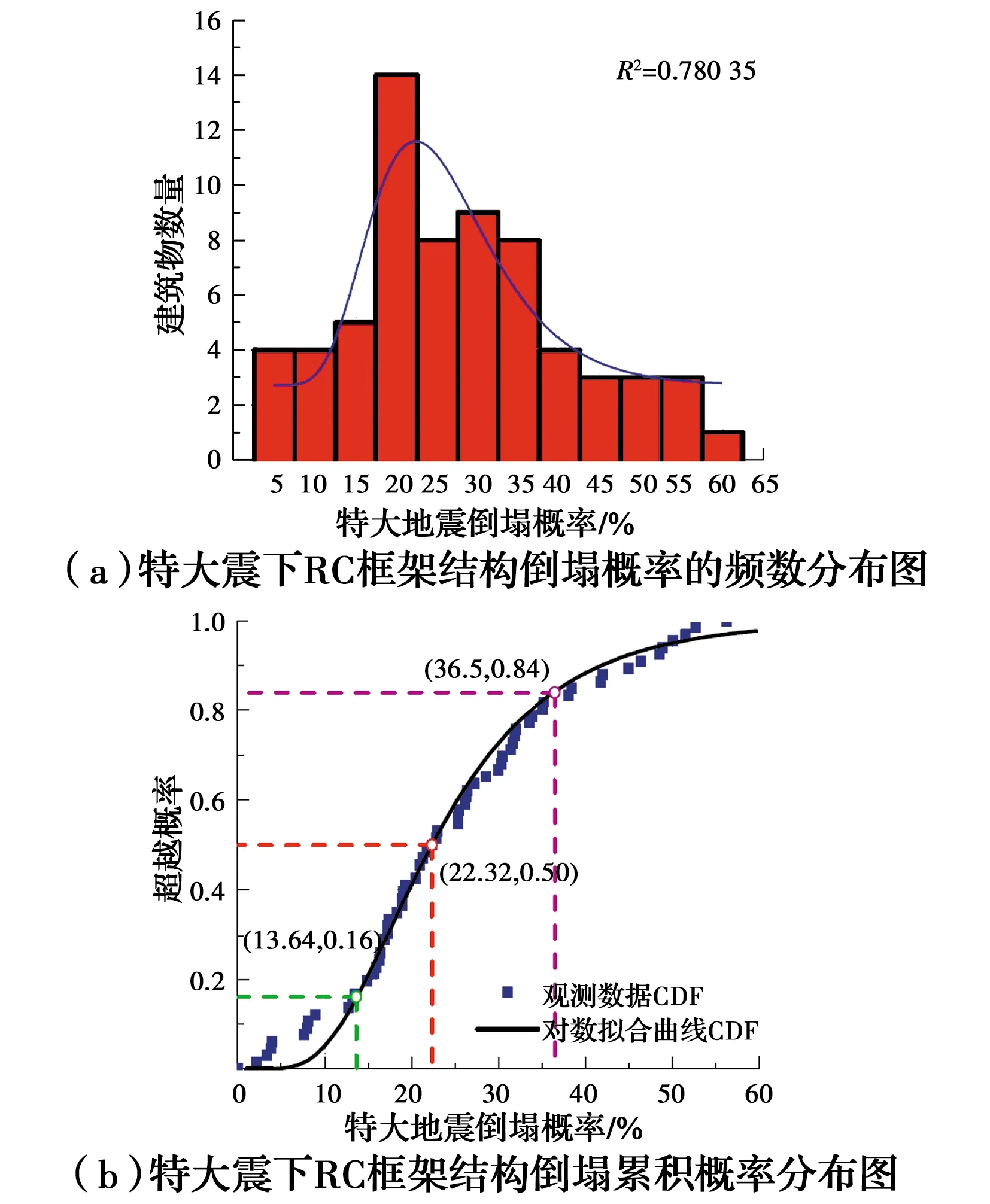
图14 特大震下RC框架结构倒塌概率的频数及累积概率分布图Fig.14 Collapse frequency and cumulative probability distribution chart of RC frame structure under severe

由表3和图14可以看出：在特大地震作用下，设计的66个典型RC框架结构中约87.9%倒塌概率在10%以上，约12.1%倒塌概率在10%以下，其倒塌概率的均值为25.16%，表明依据中国规范设计的RC框架结构抵抗特大震的能力明显不足。文献[16]对汶川地震中极震区RC框架结构的破坏情况进行了统计分析，给出了11度下RC框架的倒塌比例为23%，验证了对RC框架结构在特大震下倒塌概率的计算结果基本准确。

4 结论

基于IDA分析方法，对66个符合中国现行设计规范的典型RC框架结构进行抗地震倒塌性能分析，并剖析该类结构抗倒塌能力的概率分布，得到以下主要结论：

1)符合中国现行设计规范的RC框架结构倒塌储备系数CMR的分布范围为[1.82，7.09]，且其与结构跨度的相关性较弱，而与层数和设防烈度均为明显的负相关关系。

2)不同设防烈度下，RC框架结构的CMR平均值在7.5度设防时达最小值，表明依据中国现行规范设计的7.5度设防RC框架结构的抗倒塌能力最弱。

3)在大震作用下，符合中国现行规范的RC框架结构倒塌概率不超过10%的约有85%，而在特大地震作用下，倒塌概率不超过10%的结构仅占12.1%，表明按照现行规范设计的RC框架结构基本满足大震不倒的设防目标，但抵御特大震作用的能力明显不足。

此外，需指出的是，所设计的典型结构场地类型为Ⅱ类，设计地震分组为第二组，其研究成果仅反映该场地条件下结构的抗倒塌性能。对于其他场地条件，应该设计相应的典型结构分别进行分析。