基于吉布斯采样与压缩感知的二维非平稳CPT数据快速插值方法
朱文清,赵腾远,宋超,王宇,许领
(1. 西安科技大学 地质与环境学院,西安 710054;2.西安交通大学 人居环境与建筑工程学院,西安 710049;3. 香港城市大学 建筑学及土木工程学系,香港 999077)
岩土工程场地勘察的目标是通过室内或现场原位试验合理地描述地下土层界面并表征土层内土体物理、力学参数的空间变异性[1-2]。与室内试验[3]相比,原位测试方法,如静力触探试验[4](Cone Penetration Test,CPT)成本更加低廉、测试更加快捷[5-6]。此外,静力触探试验(CPT)能在深度方向获得近乎连续性的锥尖阻力(qc)和侧摩阻力(fs)数据,并以此作为土体的力学响应[7]。因此,CPT广泛应用于表征岩土场地参数、地下土体分层[8-11]、砂土液化评估[12-13]、确定随机场的相关函数和参数等[14-15]。
尽管CPT广泛应用于岩土场地勘察并沿深度方向获得近乎连续的土体力学响应[16],但由于工期、项目投入及技术等条件限制,在特定的工程场地或岩土工程项目中,沿水平方向的CPT钻孔数量通常很少。为解决该问题,学者们提出了众多方法来估计未采样位置处的CPT数据。例如,Fenton[17]提出了采用随机场的方法估计未采样位置的CPT数据,但该方法需要大量的CPT数据标定自相关函数。此外,该方法并未考虑CPT数据在水平方向的空间自相关性。Cai等[18]虽然考虑了水平、深度方向的相关性,并利用条件随机场来估计未采样位置的CPT数据,却依然难以回避平稳随机场假定以及参数估计问题。Juang等[19]提出了利用神经网络估计三维场地未采样位置的CPT数据。虽然该方法在数据拟合及外插上效果显著,近年来在多个领域得以应用,但由于其可解释性差,较难合理量化插值过程中产生的不确定性。量化的不确定性可以有效反映插值结果的可靠性大小。地理统计方法,如克里金法可以有效解决这一问题[20-21],但该方法仅适用于满足平稳性假设的特定土层,很难应用于地下存在多个土层且空间边界不确定的岩土工程场地。Wang等[22]提出了在CPT钻孔数据较少时利用二维贝叶斯压缩感知理论(Bayesian Compressive Sensing,BCS)[23-24]进行岩土分区。然而,由于CPT钻孔深度方向数据较多,该方法计算量大,不能高效估计未采样位置的二维CPT数据。对于具有空间变异性且边界未知的地下土层,如何正确、高效地估计未采样位置的二维非平稳CPT数据,仍然是一个重大课题。
笔者提出一种计算效率较高的无参方法,可以根据数量有限的非平稳CPT钻孔数据估计二维剖面中未采样位置的CPT数据。该方法结合压缩感知(Compressive Sensing,CS)、贝叶斯框架、吉布斯采样[25-26],并引入可快速更新计算结果的克罗内克积,以提高计算效率。与已有文献相比,该方法在估计二维CPT数据方面计算效率显著提高。此外,相比于随机场模型,该方法回避了自相关函数模型选择与参数估计、数据平稳性、高斯分布等假设;相比于神经网络,该方法可以合理确定CPT钻孔数目少带来的不确定性。值得注意的是,该方法要求不同CPT钻孔沿深度方向的力学响应数据一致。
1 二维CPT数据的贝叶斯压缩感知
1.1 二维贝叶斯压缩感知框架
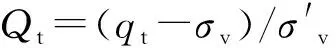
(1)

(2)
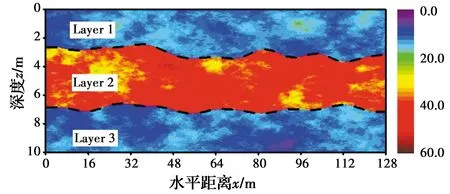
图1 有两个土层边界的二维非平稳Qt数据Fig.1 A set of 2D non-stationary Qt data with two

图2 CPT测深位置及孔内Qt随深度的变化曲线Fig.2 CPT sounding locations and variation curves
1.2 二维CPT数据与的关系
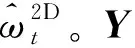
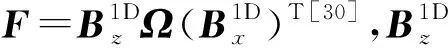
(3)
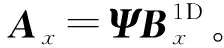
(4)

(5)

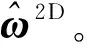
(6)
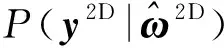
(7)
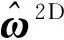
(8)
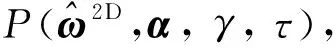
(9)
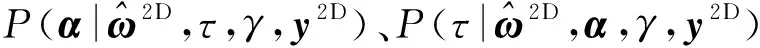
(10)
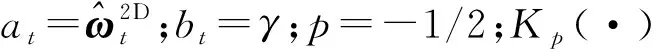
(11a)
(11b)

2.1 吉布斯采样(phthalic anhydride)

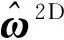
(12)
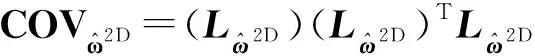
(13)
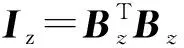
(14)
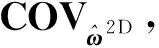
(15)
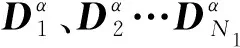
(16)
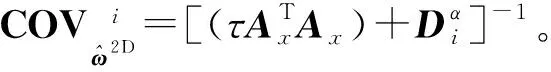

(17)

(18)
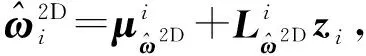
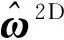

图3 生成二维CPT数据的流程图Fig.3 A flow chart for simulating 2D CPT

图4 引入克罗内克积吉布斯采样的伪代码Fig.4 Pseudo code for fast simulation of using the Gibbs sampling method with Kronecker
3 数值模拟案例
为了验证该方法,选取一组分布在3层土层内的二维CPT锥尖阻力(Qt)数据,如图1所示。此例中,采用高斯平稳随机场生成器(如循环嵌入算法)在垂直方向和水平方向分别以ηz=0.02 m和ηx=0.5 m的分辨率生成每层内的Qt数据[39]。随机场模拟中涉及的参数包括Qt的均值、标准差SD、垂直方向以及水平方向相关长度λz和λx。第1~3层的均值分别取为12、40和12;SD分别为2、5和2;相关长度分别为λz=2 m和λx=20 m,与文献[40]一致。在生成每层Qt数据时采用单指数自相关函数
(19)
式中:Δz=zi-zm和Δx=xj-xn分别表示位置(zi,xj)和(zm,xn)沿z和x方向的相对距离。利用上述随机场参数和随空间变化的岩土层边界,可获得3层内的非稳态二维Qt数据,如图1所示。尽管每层中的Qt数据是稳态的,但由于不同土层中Qt的统计量不同,图1所示的二维数据集是非稳态的。
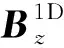

图5 二维CPT数据模拟结果示例Fig.5 Two examples of simulated 2D CPT
为了说明引入克罗内克积对计算效率的提升,记录生成上述100个独立CPT样本的时间,见表1。由表1可见,使用64位Windows 10操作系统的Intel©Core®i7-9700 3.0 GHz CPU和16.0 GB RAM的计算机,生成100组独立二维CPT样本大约需40.6 s。然而,若不采用序列更新方法,即直接采用式(12)生成样本时,同一台计算机上大约需1 421.2 s。相比于原始方法,该算法在计算效率上提高了约35倍。随着CPT勘测钻孔数量nb的增加,使用序列更新技术的计算效率提高会更为明显。
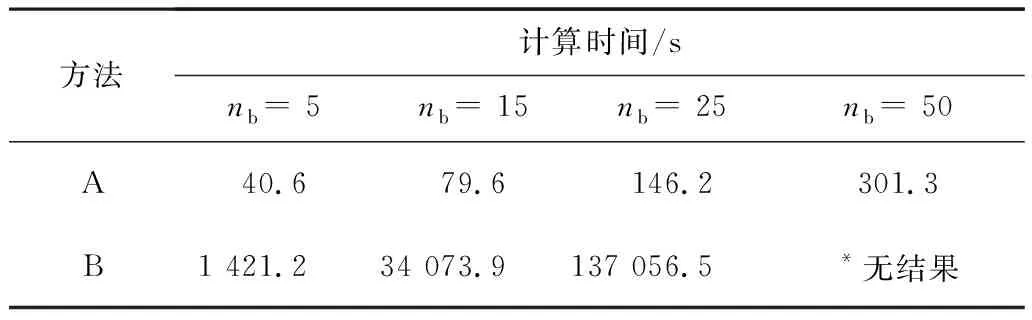
表1 不同CPT钻孔数目下,使用序列更新技术(A)和不使用序列更新技术(B)生成100组二维Qt样本的计算时间
*注:因运算所需内存过大,方法B在笔者电脑中无法运行。
利用上述100个二维Qt样本可得其均值,如图6所示。结果表明,即使在未知地下边界处,Qt均值的分布也与图1所示较为一致。表明利用该方法生成的二维非稳态Qt样本在统计上保留了图1中Qt原始数据的非稳态模式。此外,根据生成的二维Qt样本还可计算每一点的标准差,见图7。结果表明,CPT钻孔位置处的标准差非常小,说明在这些位置估计的Qt可靠性和可信度较高。因为这些位置的Qt数据已知,并将其作为建议方法的输入。相反,因为远离测量点的位置有效信息极少,导致远离CPT钻孔位置的样本标准差相对较大。
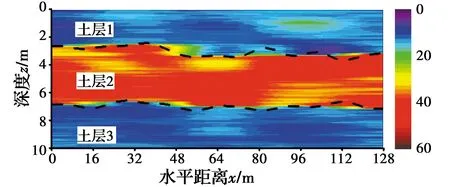
图6 MCMC模拟Qt数据的均值Fig.6 Averaged Qt from the simulated MCMC

图7 MCMC模拟Qt数据的标准差Fig.7 SD of Qt from the simulated MCMC
为了进一步验证该方法插值的合理性,比较图2(a)中4个未测量钻孔(即BH1、BH2、BH3、BH4)的Qt数据。图8(a)~(c)分别以虚线绘制了该方法在这4个钻孔位置插值的Qt数据。为进行比较,图8以粗线给出了BH1至BH4处的原始Qt变化曲线。图8显示,每个子图中虚线的变化趋势与实线一致,表明利用提出的方法生成的Qt样本是合理、可靠的,并较为合理地刻画了图1中CPT数据的非平稳特点。
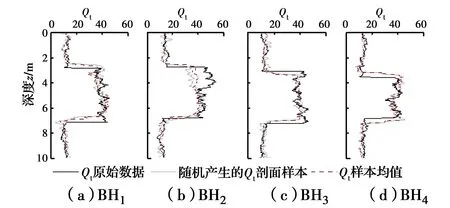
图8 位置BH1到BH4处的Qt均值与原始数据的对比Fig.8 Comparison between averaged Qt profile and the original one at locations BH1 to
值得注意的是,图8中虚线、灰线和粗实线之间存在一些差异。这是因为使用提出的方法时,输入的CPT钻孔数量较少。当nb增加时,二维Qt样本会更加接近CPT真实数据。
4 CPT测深数量的影响
采用nb=5、15、25和50的案例探讨该方法的性能。对于每个nb案例,前述方法随机生成100个独立的二维Qt样本,然后利用这100个Qt样本计算每个位置的Qt均值及标准差,详见图9、图10。由图9可以看出,随着nb的增加,每个位置的Qt样本均值越来越接近于图1。当nb=25时,Qt样本均值与实测Qt几乎相同。此外,图10显示,随着nb的增加,每个位置估算的Qt标准差不断减小,表明每个位置Qt估算值的可靠性和置信度都有所提高。该计算结果反映了本文所提方法的数据驱动本质。
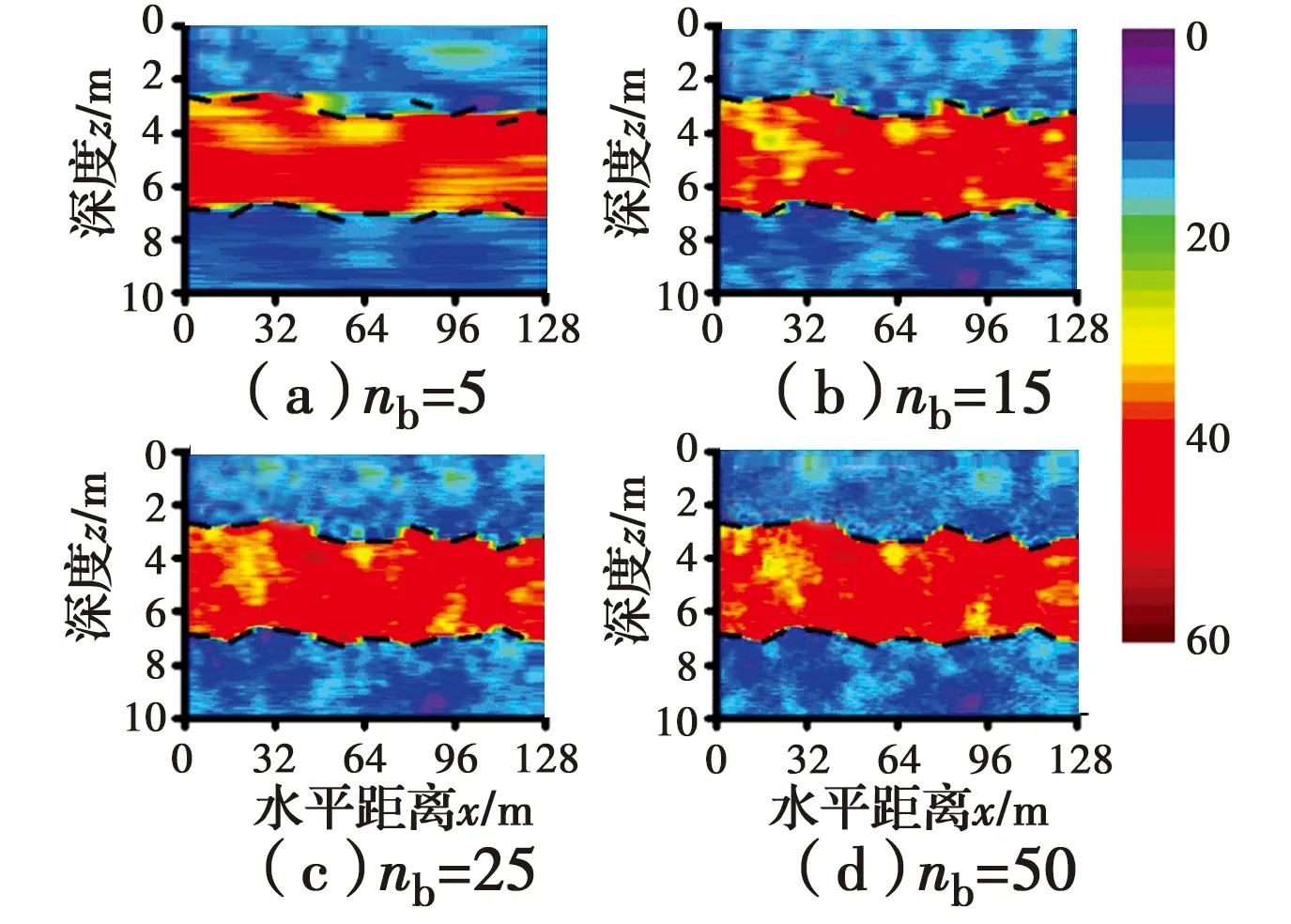
图9 nb对二维Qt样本均值的影响Fig.9 Effect of nb on 2D Qt averaged

图10 nb对MCMC样本二维Qt数据标准差的影响Fig.10 Effect of nb on SD of 2D Qt estimated from
另外,随着nb的增加,采用序列更新技术的计算时间会略有延长,如表1所示。但与不采用序列更新技术的方法相比,该方法所增加的计算时间几乎可以忽略。当nb=15时,该方法仅需约79.6 s,而未采用序列更新技术的方法需9 h以上(见表1)。两种方法计算时间的差距表明,所提出的方法可显著提高计算效率。
值得强调的是,该方法可以较为合理地考虑CPT钻孔数量导致的不确定性,为了定量说明不确定性的大小,根据图9、图10分别计算出了nb=5、15、25、50不同情况下变异系数 (δ=σ/μ×100%)的中位数,分别是11.80%、10.86%、9.36%与8.10%。此外,根据计算经验,该方法能适用的最少CPT钻孔数在4~5个左右,如果CPT钻孔更少,应谨慎使用该方法。
5 工程应用
为进一步验证方法的有效性,选取位于日本冈山河堤的某工程场地进行验证研究。该场地自上而下主要由砂土、黏土或粉土、砂土组成。其中上层砂土厚约2 m,黏土最厚约3 m,粉土厚约1~2 m,粉土下面仍主要以砂土为主。为了探明该河堤的软土空间分布,日本工程师在此进行了一系列的CPT。选取其中的CPT-201~CPT-207来验证该方法。图11给出了上述7个CPT钻孔的位置分布图,其中,CPT-204用来验证,其余CPT标准化Qt数据当作输入。所有的数据均来自TC304免费数据库(http://140.112.12.21/issmge/tc304.htm)。按照该方法,可以得到Qt的二维剖面分布,其均值与标准差见图12。由图12可知,估计的Qt数据离CPT钻孔位置愈接近,对应的标准差愈小,反之,则愈大。由于这是真实原位试验数据,无法得知CPT-204以外的真实数据。这里以CPT-204对应的Qt数据与此位置的估计数据进行对比,见图13。图13显示,虽然估计值与试验值之间存在一定差距,但两者趋势基本一致;此外,CPT-204的大部分实测试验值落在估计值的95%置信区间里,间接说明该方法的准确性以及鲁棒性。

图11 CPT钻孔201到207分布图Fig.11 Spatial distribution of CPT soundings ranging
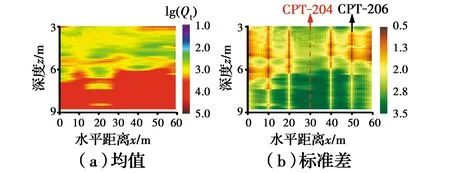
图12 日本冈山河堤Qt剖面估计结果Fig.12 Estimated Qt profile of the Okayama Riverbank in
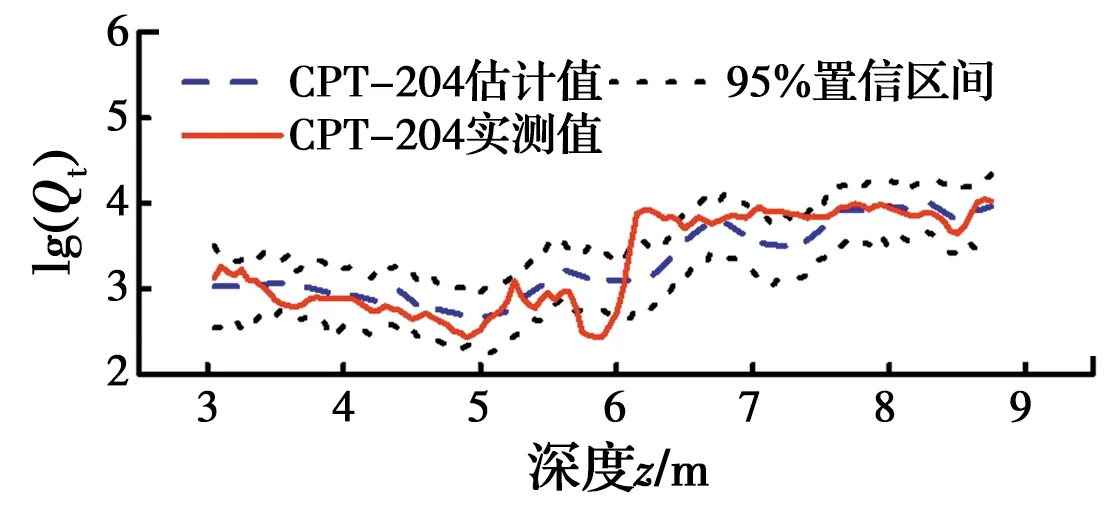
图13 CPT-204估计值与实测值的对比Fig.13 Comparison between predicted and measured
6 结论
基于吉布斯采样与贝叶斯压缩感知方法,提出了一种快速估计未采样位置的非平稳静力触探测试数据(CPT)的方法。该方法属于无参估计范畴,能够自动考虑静力触探数据沿水平方向的相关性,同时回避了水平、深度方向自相关函数的采用以及数据平稳性等假设。生成的CPT数据可用于解决各种岩土工程和地质工程问题,如土壤分层和分区、土壤液化潜力评估及其空间变异性表征、岩土设计参数的间接估计等。该方法为解决实际工程问题提供了一种概率工具,尤其是针对在实践中经常遇到的沿水平方向的CPT勘测钻孔数量较少的情况。最后,通过数值与实际工程案例对提出的方法进行验证,结果表明,该方法较为准确,并且采用序列更新技术后可显著提高计算效率,具有较强的鲁棒性。

