基于阵列处理器的最小均方误差检测算法并行设计与实现

刘帅，蒋林，李远成，山蕊，朱育琳，王欣

（1.西安科技大学 通信与信息工程学院，西安 710054； 2.西安科技大学 计算机科学与技术学院，西安 710054；3.西安邮电大学 电子工程学院，西安 710121； 4.西安科技大学电气 与控制工程学院，西安 710054）（∗通信作者电子邮箱jianglin@xust.edu.cn）

基于阵列处理器的最小均方误差检测算法并行设计与实现

刘帅1，蒋林2*，李远成2，山蕊3，朱育琳4，王欣4

（1.西安科技大学 通信与信息工程学院，西安 710054； 2.西安科技大学 计算机科学与技术学院，西安 710054；3.西安邮电大学 电子工程学院，西安 710121； 4.西安科技大学电气 与控制工程学院，西安 710054）（∗通信作者电子邮箱jianglin@xust.edu.cn）

针对大规模多输入多输出（MIMO）系统中，最小均方误差（MMSE）检测算法在可重构阵列结构上适应性差、计算复杂度高和运算效率低的问题，基于项目组开发的可重构阵列处理器，提出了一种基于MMSE算法的并行映射方法。首先，利用Gram矩阵计算时较为简单的数据依赖关系，设计时间上和空间上可以高度并行的流水线加速方案；其次，根据MMSE算法中Gram矩阵计算和匹配滤波计算模块相对独立的特点，设计模块化并行映射方案；最后，基于Xilinx Virtex-6开发板对映射方案进行实现并统计其性能。实验结果表明，该方法在MIMO规模为、和的正交相移键控（QPSK）上行链路中，加速比分别2.80、4.04和5.57；在的大规模MIMO系统中，可重构阵列处理器比专用硬件减少了42.6%的资源消耗。

大规模多输入多输出；最小均方误差算法；并行映射；阵列处理器；可重构

0 引言

大规模多输入多输出（Multiple-Input Multiple-Output， MIMO）技术是未来移动通信的关键技术之一［1］。随着基站端天线数持续上涨，上行链路信号检测面临巨大挑战，信号检测器对计算精度、硬件复杂度和算法并行性提出了更高要求。因为信道矩阵向量在多用户理想传播条件下会表现出渐进正交性，所以最小均方误差（Minimum Mean Square Error， MMSE）算法就可以达到较为理想的信号检测精度，它在实际大规模MIMO系统中具有很大的应用潜力［2］。可重构是一种使用软件编程去改变重构信息，最终使硬件功能得到改变的技术［3］，其兼具通用处理器的灵活性和专用集成电路（Application Specific Integrated Circuit， ASIC）的高性能。可重构阵列结构能较好地平衡资源消耗与计算效率的关系，因此基于该结构的信号检测器具有光明的发展前景。

然而，基于可重构结构的大规模MIMO信号检测算法的实现还存在一些问题。

一方面，目前基于可重构结构的信号检测器大部分面向传统规模的MIMO系统，架构扩展性不足。文献［4］中提出了一种由20个运算单元（Process Element， PE）和1个Center Alpha单元构建的粗粒度可重构架构（Coarse Grained Reconfigurable Architecture，CGRA），虽然该结构可以通过处理器集成的指令灵活地实现多种算法，但是固定的PE阵列限制了MIMO规模扩展；文献［5］中基于动态可重构处理器架构，实现了线性最小均方误差（Linear Minimum Mean Square Error， LMMSE）信道估计算法，其处理速度达到了通用微处理器的8.8～14.6倍，但仅支持的矩阵规模；文献［6］中采用一种异构可重构阵列处理器实现了高效率和低能耗的信号检测，但是该阵列结构只支持的MIMO规模，无法满足当前大规模MIMO的检测需求。

另一方面，基于现场可编程门阵列（Field Programmable Gate Array， FPGA）的大规模MIMO检测架构会造成较高的硬件开销。文献［7］中使用并行切比雪夫算法实现了的大规模MIMO信号检测，虽然该算法通过迭代将矩阵乘法转化为矩阵和向量相乘，降低了计算复杂度，但是复杂的迭代控制增加了FPGA实现难度，并消耗了过多资源；文献［8］中提出了一种递推共轭梯度迭代方法进行信号检测，并设计了基于该方法的、64正交幅度调制（Quadrature Amplitude Modulation， QAM）大规模MIMO系统硬件架构，但是该架构中包含了6种不同结构的PE，对硬件资源消耗和设计复杂度有较大挑战。

为了使大规模MIMO系统中MMSE检测算法适应可重构结构，解决MMSE算法中矩阵计算复杂度高、运算效率低的问题，本文基于项目组开发的同构轻核可重构阵列处理器平台［9］，设计了MMSE算法在可重构阵列处理器上并行映射的方案，最终以较高的计算效率和较低资源消耗实现了大规模MIMO信号检测。

1 大规模MIMO检测算法分析

对于复杂大规模MIMO信道条件，MMSE算法考虑到了噪声影响，于是估计的发送信号计算式如式（2）所示：

图1 MMSE检测算法运算流程Fig. 1 Calculation flow of MMSE detection algorithm

表1 不同下的特征Tab. 1 Characteristics of at different

表1 不同下的特征Tab. 1 Characteristics of at different

的计算结果运算复杂度123

2 MMSE算法并行映射方案设计

2.1 阵列处理器的硬件结构

本文方案采用项目组提出的基于H型传输网络的可重构阵列处理器实现。该处理器使用FPGA架构设计，由主机接口、全局控制器、可重构处理单元、输入存储器和输出存储器五部分构成，其结构如图2所示。

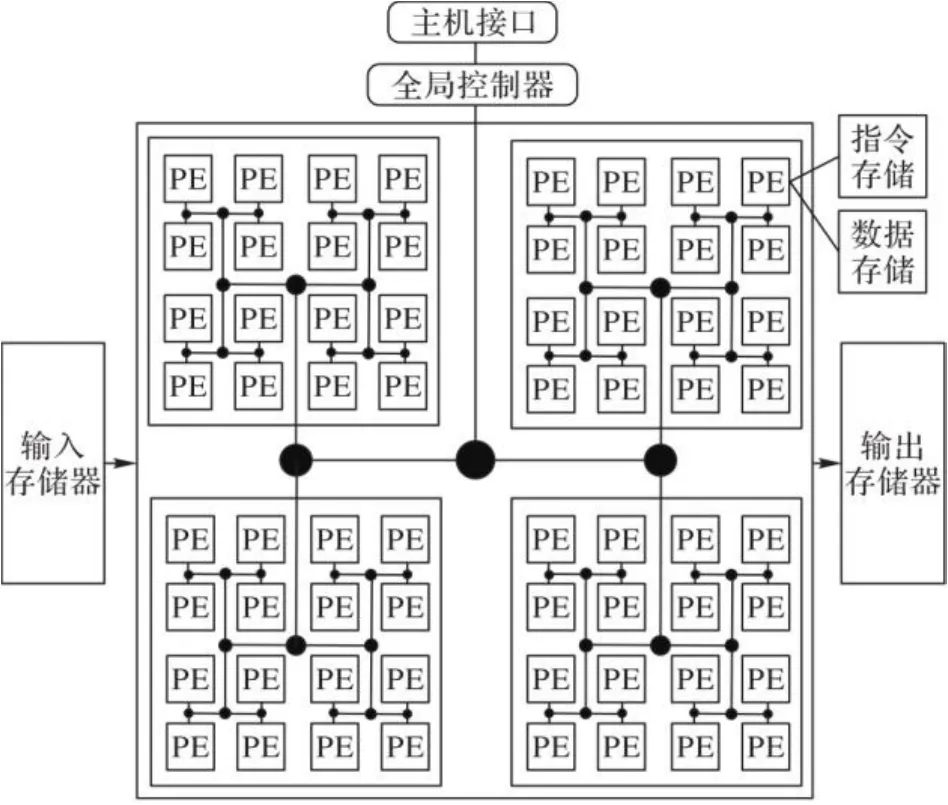
图2 阵列处理器结构Fig. 2 Structure of array processor

可重构处理单元是阵列处理器的核心，由1 024个PE构成，每一组的PE阵列构成一个处理单元簇（Process Element Group， PEG），简称为簇。图2中只展示出了4个簇，其余簇可以在该架构上进行扩展。每个PE包含了1个数据和1个指令存储单元。数据存储单元有512行，每行位宽为16 b；指令存储单元也有512行，但指令位宽为32 b。相邻PE之间可采用邻接互连方式传递数据，相邻簇间可通过路由方式传递数据。主机接口负责将上位机下发的命令传输到全局控制器；全局控制器将主机接口接收的信息分为数据流和指令流，通过H树网络进行调度，并合理分配到每个PE中；输入存储器用于存储计算时的输入数据；输出存储器用来把计算结果进行输出。因为PE功能会根据配置信息的不同而发生改变，所以可重构阵列处理器具有高灵活性［15］。

2.2 并行映射方案设计

2.2.1 Gram矩阵并行计算方案设计

则有式（4）成立：

在式（4）中，只需计算上三角元素和对角元素，便可得到全部矩阵元素。观察矩阵中每一个元素，发现每行均有相同行向量，每列均有相同列向量，此数据特征非常适合采用流水线结构设计复数矩阵乘法。

阵列处理器中一个簇有16个PE，考虑到MIMO规模的扩展性，首先在的MIMO规模下使用4个PE完成Gram矩阵并行计算。具体映射方案如下：

2）数据传输。PE00为最先开始数据传输的PE，当指令读取到的第1个元素后，将共轭变化为的第1个元素，并把依次传输到PE10、PE20和PE30中。

图3中，每一列为Gram矩阵一个元素的计算周期，每一行为每个PE需要执行的操作，每一个方格代表了不同计算周期内PE中的一个操作。由图3可以看出，在不考虑数据流动延迟的情况下，采用流水线模式计算Gram矩阵，仅仅需要4个计算周期就可以完成全部计算。然而采用串行方式逐个计算Gram矩阵元素时，即使考虑到埃尔米特矩阵共轭转置特性，也需要依次计算4个对角元素和6个非对角元素，这会消耗10个计算周期。所以从理论上来讲，在的MIMO规模下，并行Gram矩阵计算相较于串行计算能够取得加速比为2.5。在一个簇中，、和的Gram矩阵并行计算映射分别如图4所示。

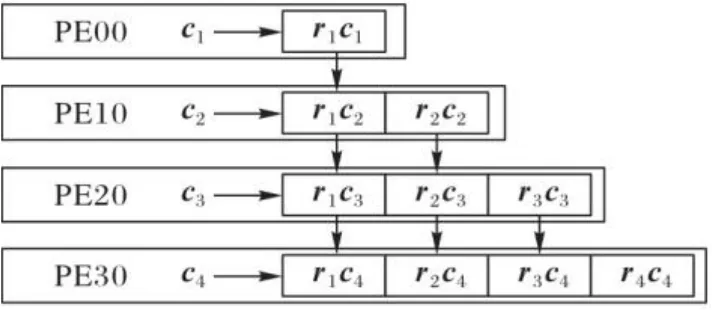
图3 流水线结构映射Fig. 3 Pipeline structure mapping

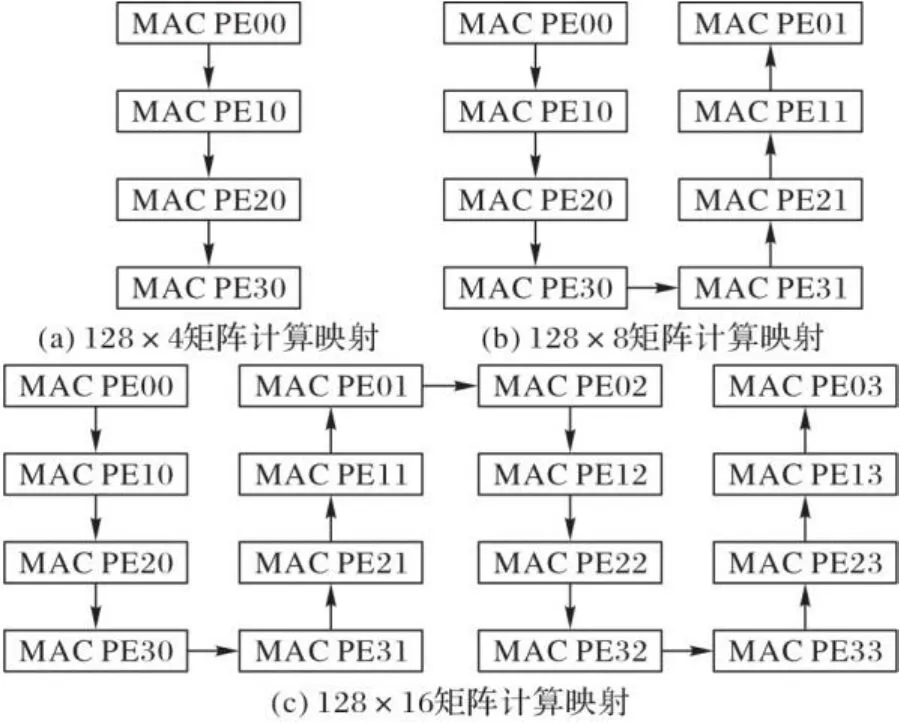
图4 Gram矩阵并行计算映射Fig. 4 Mapping of Gram matrix parallel computing

在图4中，为了降低数据传输延迟、减少计算时数据等待时间，于是在相邻PE之间采用了邻接互连的蛇形数据传输方式。各个PE的计算模式相同，唯一不同的是计算量，从箭头指向的第一个PE到最后一个PE，计算量依次递增。每个PE按箭头指向顺序依次存储矩阵的列向量。如在128×4的MIMO规模下，PE00、PE10、PE20和PE30中分别存储、、和的数据，并在这4个PE中完成矩阵计算。

为了统计矩阵计算时间，规定一个计算周期即为完成Gram矩阵中一个元素计算所需时间，该时间由两组拥有128个复数的数组对应完成乘累加组成。采用流水线结构加速计算时，并行计算周期数取决于Gram矩阵对角线元素个数。串行计算周期数由对角线元素个数和上三角元素个数相加组成。在的MIMO规模下，Gram矩阵有8个对角线元素和28个上三角元素，所以并行计算周期是8，串行计算周期是36。图4（c）中，在的MIMO规模下使用了16个PE完成了Gram矩阵计算，因为Gram矩阵有16个对角线元素和120个上三角元素，所以并行计算周期是16，串行计算周期是136。在不同MIMO规模下，Gram矩阵对应的计算周期和理论加速比如表2所示。

从表2可以看出，随着MIMO规模增加，无论是串行还是并行方案，Gram矩阵的计算周期都会增长。串行方案全部使用1个PE完成计算，并行方案下使用的PE数量与Gram矩阵中对角线元素数量保持一致，且与MIMO规模中用户端天线数相同。矩阵计算的理论加速比会随着MIMO规模增大而提高，此特点有利于更大规模的MIMO系统中信号检测算法高效执行。

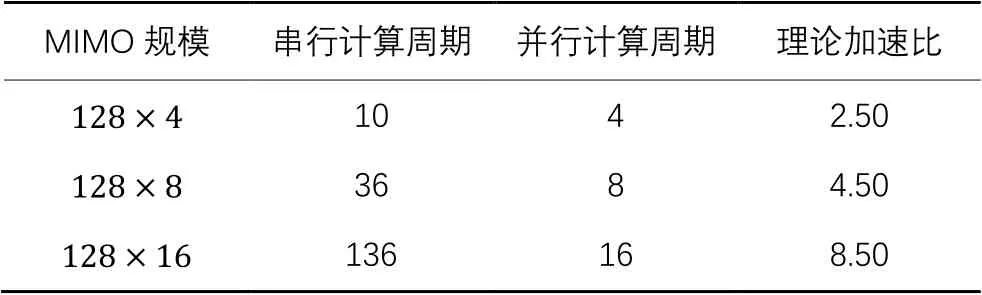
表2 Gram矩阵计算的理论值Tab. 2 Theoretical value of Gram matrix calculation

2.2.2 模块化并行方案设计

根据图1运算流程，如果把Gram矩阵计算替换为并行计算，可得并行映射方案①。由于Gram矩阵计算和匹配滤波计算不具备数据依赖关系，所以在执行Gram矩阵并行计算时，让匹配滤波计算同时开始执行，完成模块化并行，则可得并行映射方案②。

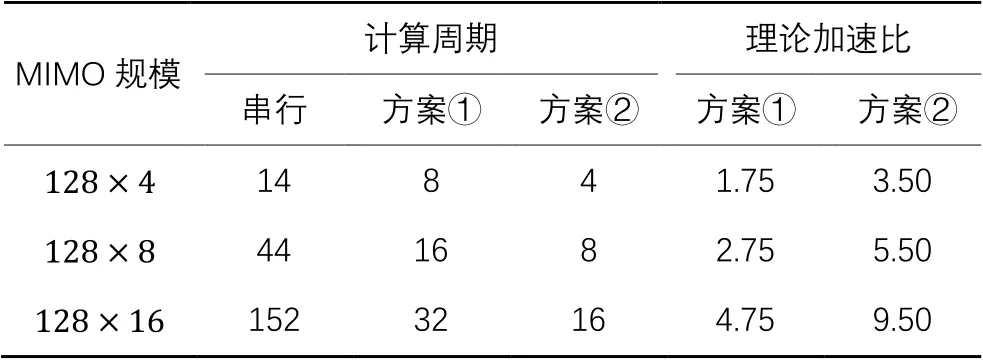
表3 Gram矩阵和匹配滤波计算的理论值Tab. 3 Theoretical values of Gram matrix and matched filter calculation

与表2相比，表3中方案①的计算周期只是在表2中并行计算周期的基础上加上了的计算周期。方案②中模块化并行会使加速比提高至方案①的2倍。因为在理想状况下，与的计算周期相同，并行计算时这两个矩阵计算同时开始、同时结束，只占用了个计算周期；所以模块化并行会进一步降低计算耗时，提高计算效率。

2.2.3 PE功能设计

虽然矩阵求逆时使用纽曼级数近似算法能够降低求逆复杂度，但是纽曼级数法各个计算步骤之间有很强的数据相关性，故只能逐步顺序执行。通过表1可知，当时，纽曼级数法兼顾了计算复杂度与准确性的要求，于是有式（5）：

把式（5）中各个计算单元重新命名，可得式（6）、式（7）和式（8）分别如下：

对算法进行实现时，方案中用户端天线数分别设计为4、8和16。当等于16时，由于矩阵每个元素的实部和虚部各占用一行存储单元，故存储一个矩阵需要512行存储单元，即一个PE。虽然PE中可以同时存储指令与数据，但是为了在计算时避免地址冲突，与矩阵大小相同的矩阵、、的数据必须单独存储在一个PE中。于是，Gram矩阵串行计算、匹配滤波计算、矩阵求逆和信道均衡的任务只能把指令和数据划分给不同PE进行存储。因为在的MIMO规模下，Gram矩阵并行计算在一个簇中PE的使用率为100%，故选取其展现完整的MMSE检测算法并行映射方案如图5所示。

图5中，PEG00完成Gram矩阵计算的任务，PEG01完成匹配滤波、矩阵求逆和信道均衡的任务，阴影部分为存储数据的PE，非阴影部分为执行计算功能的PE。在PEG00中，与图4（c）相比，PE03增加了把计算完成的Gram矩阵元素传输给PEG01的任务。

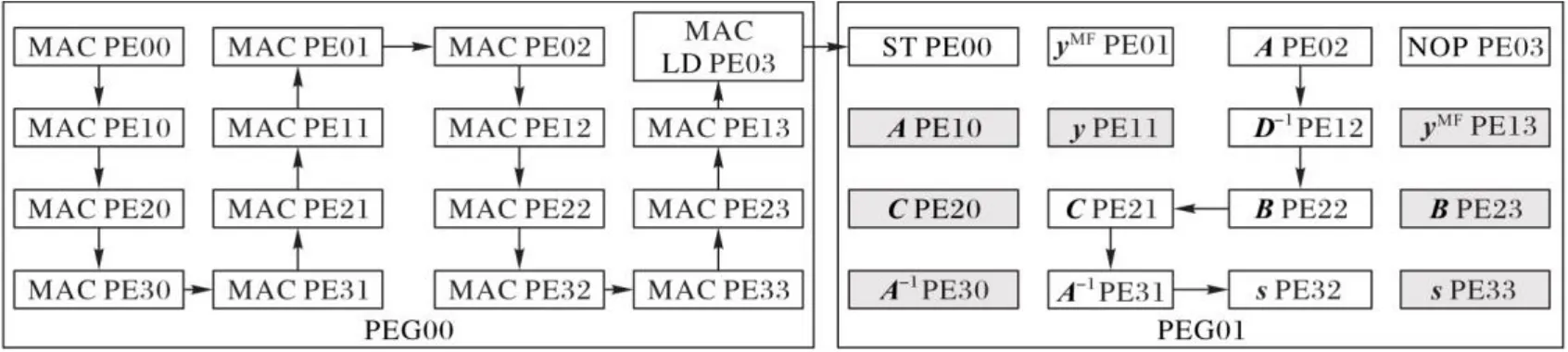
图5 MMSE算法并行映射Fig. 5 Parallel mapping of MMSE algorithm

3 实验与结果分析

3.1 实验环境和步骤

本文先使用Matlab建模生成实验数据：首先，产生一组随机的二进制比特流，经过QPSK调制后得到发送信号；其次，随机生成一组矩阵元素独立同分布，且实部与虚部都服从零均值和单位方差高斯分布的信道矩阵；然后，生成加性高斯白噪声向量，由控制生成噪声功率谱密度；最后，根据式（1）计算接收信号。

实验数据生成以后，使用BEEcube公司BEE4开发平台上的Xilinx Virtex-6 XC6VLX550T FPGA搭建的阵列处理器原型系统进行FPGA验证和测试。具体实现步骤如下：

2）使用专用指令集完成算法的代码级描述，并通过翻译器将指令翻译为二进制，输入到指令存储单元。

3）利用QuestaSim 10.1d仿真软件在阵列处理器上对串并行映射方案进行仿真，验证算法映射的正确性。

4）采用ISE 14.7开发环境对设计进行逻辑综合，根据综合实现结果分析性能。

5）在BEE4平台上进行FPGA硬件实现，验证实验结果的合理性。

3.2 结果分析

首先，对Gram矩阵计算的串行和并行方案进行仿真，计算实际加速比。MIMO规模分别为、和，结果如表4所示。

从表4可以看出，Gram矩阵计算的实际加速比与理论加速比大致相当，表明Gram矩阵计算的映射方案可行。然而，随着MIMO规模中用户端天线数增加，理论加速比与实际加速比的差值会越来越大。出现此现象的主要原因是，使用流水线方式加速计算时，用户端天线数的增加导致并行计算使用的PE数量增加，首个PE下发的数据会经过更长时间才能传输到最后一个PE中，所以更多的数据传输时延将会导致并行计算时间增加，进而降低实际加速比。

表4 Gram矩阵计算仿真结果Tab. 4 Simulation results of Gram matrix calculation

其次，统计分别在方案①和方案②下完成Gram矩阵计算和匹配滤波计算后的实际加速比，实验结果如表5所示。通过表5可以发现，方案①中完成前两个模块计算的实际加速比很接近理论值，理论与实际的误差仅在0.2以内。方案②中由于数据传输延迟，导致Gram矩阵计算时间多于匹配滤波计算时间，进而延长了模块化并行时间，于是实际加速比下降过大。但是从整体上来说，方案②的加速性能优于方案①。上述结果表明，在模块化并行映射方案下，MMSE算法能够获得更高的运行效率。

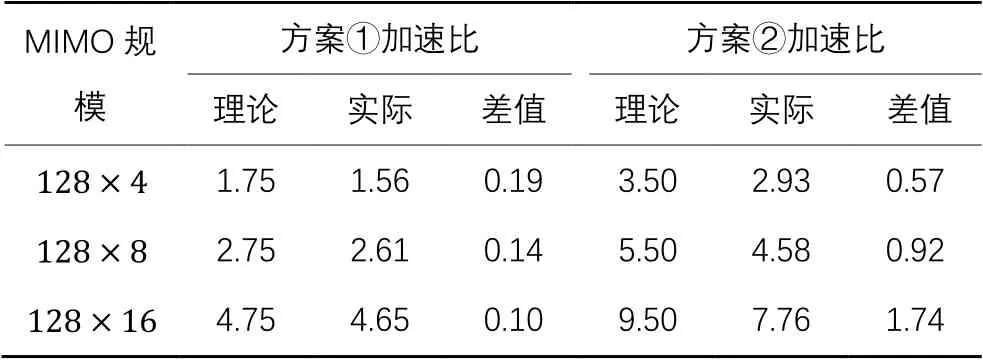
表5 Gram矩阵和匹配滤波计算仿真结果Tab. 5 Simulation results of Gram matrix and matched filter calculation

最后，对整个MMSE算法进行仿真。统计方案①和方案②的加速比，结果如图6所示。从图6可以看出，方案②的加速比在、和的MIMO规模下分别为2.80、4.04和5.57，平均提升至方案①的1.64倍。该性能提升对低时延要求的大规模MIMO系统具有重大意义。

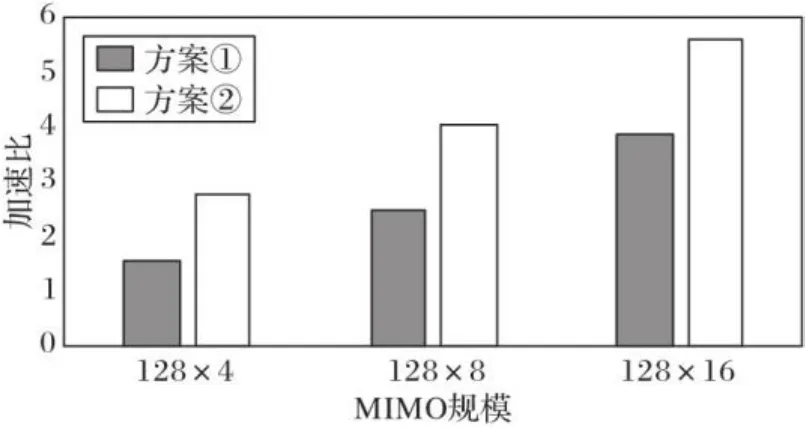
图6 并行映射加速比Fig. 6 Acceleration ratio of parallel mapping

图7 不同MIMO规模下的相对误差Fig. 7 Relative errors under different MIMO scales

表6 不同方法FPGA实现结果比较Tab. 6 Comparison of FPGA implementation results by different methods

文献［7］方法在MIMO规模与本文实验相同的条件下，虽然工作频率获得了提升，但是本文方法的硬件资源消耗，即查找表（Look-Up Table， LUT）和触发器（Flip-Flop， FF）资源之和却比文献［7］方法降低了42.6%。在文献［11］方法和文献［16］方法中，MIMO规模为，远小于本文方法的MIMO规模，但是本文方法相较文献［11］方法和文献［16］方法方法分别节约了77.7%和63.9%的硬件资源。因为MIMO规模越大，需要执行的计算越复杂，消耗的资源越多，所以如果将文献［11］方法和文献［16］方法中MIMO规模扩大为，资源消耗量还会提高。根据本文中可重构阵列处理器指令集的特点，乘法运算会分解为基本的加法和移位操作进行处理，这会极大降低硬件资源消耗，所以本文方法在资源消耗量方面具有优势。

综合上述实验结果可以看出，本文提出的基于可重构阵列处理器的并行映射方法能够有效减少MMSE算法的执行时间，虽然输出结果会有部分精度损失，但是该方法具有灵活的映射结构和较小的资源消耗。

4 结语

本文提出了一种基于阵列处理器的MMSE算法并行映射方法，在QPSK调制方式的上行链路中，实现了大规模MIMO信号检测。该并行映射方法将MMSE算法执行分为计算并行和模块化并行，在计算并行中设计了流水线结构的Gram矩阵计算方式，在模块化并行中设计了匹配滤波计算和Gram矩阵计算同步执行的方案。实验结果表明，在、和的MIMO规模下，MMSE算法的加速比分别达到了2.80、4.04和5.57；与文献［7］方法相比，本文方法资源消耗降低了42.6%。本文方法不仅体现了阵列结构的灵活性，而且还验证了该结构在硬件资源消耗量方面占有优势。后续研究将对硬件结构进行优化，以进一步提高信号检测算法的计算精度和执行效率。

[1] HARRIS P， MALKOWSKY S， VIEIRA J， et al. Performance characterization of a real-time massive MIMO system with LOS mobile channels ［J］. IEEE Journal on Selected Areas in Communications， 2017， 35（6）： 1244-1253.

[2] PENG G Q， LIU L B， ZHOU S， et al. A 1.58 Gb/s/W 0.40 Gb/s/mm2ASIC implementation of MMSE detection for64-QAM massive MIMO in 64 nm CMOS ［J］. IEEE Transactions on Circuits amp; Systems I： Regular Papers， 2018， 65（5）： 1717-1730.

[3] 魏少军，李兆石，朱建峰，等.可重构计算：软件可定义的计算引擎［J］.中国科学：信息科学，2020，50（9）：1407-1426.（WEI S J， LI Z S， ZHU J F， et al. Reconfifigurable computing： toward software defifined chips ［J］. SCIENTIA SINICA Informationis， 2020， 50（9）： 1407-1426.）

[4] CHEN X L， MINWEGEN A， HUSSAIN S B， et al. Flexible， efficient multimode MIMO detection by using reconfigurable ASIP［J］. IEEE Transactions on Very Large Scale Integration Systems， 2015，23（10）： 2173-2186.

[5] 赵灿坤，王自强.基于动态可重构处理器的信道估计算法实现［J］.微电子学与计算机，2020，37（7）：1-5，11.（ZHAO C K， WANG Z Q. Implementation of channel estimation algorithms based on dynamic reconfigurable processor ［J］. Microelectronics and Computer， 2020， 37（7）： 1-5， 11.）

[6] ZHANG C X， LIU L， MARKOVIC D， et al. A heterogeneous reconfigurable cell array for MIMO signal processing ［J］. IEEE Transactions on Circuits amp; Systems I： Regular Papers， 2015， 62（3）： 733-742.

[7] PENG G Q， LIU B L， ZHANG P， et al. Low-computing-load， high-parallelism detection method based on Chebyshev iteration for massive MIMO systems with VLSI architecture ［J］. IEEE Transactions on Signal Processing，2017， 65（14）： 3775-3788.

[8] LIU L B， PENG G Q， WANG P， et al. Energy- and area-efficient recursive-conjugate-gradient-based MMSE detector for massive MIMO systems ［J］. IEEE Transactions on Signal Processing， 2020， 68： 573-588.

[9] 蒋林，贺飞龙，山蕊，等.可重构视频阵列处理器测试平台设计与实现［J］.系统仿真学报，2020，32（5）：792-800.（JIANG L， HE F L，SHAN R， et al. Design and implementation of reconfigurable video array processor test platform ［J］. Journal of System Simulation， 2020， 32（5）： 792-800.）

[10] GAO X， DAI L， MA Y， et al. Low-complexity near-optimal signal detection for uplink large-scale MIMO systems ［J］. Electronics Letters， 2014， 50（18）： 1326-1328.

[11] WU M， YIN B， WANG G H， et al. Large-scale MIMO detection for 3GPP LTE： algorithms and FPGA implementations ［J］. IEEE Journal of Selected Topics in Signal Processing， 2014， 8（5）： 916-929.

[12] 金凤，唐宏，张进彦，等.基于压缩感知的大规模MIMO系统导频优化及信道估计算法［J］.计算机应用，2018，38（5）：1447-1452.（JIN F，TANG H， ZHANG J Y， et al. Pilot optimization and channel estimation in massive multiple-input multiple-output systems based on compressive sensing ［J］. Journal of Computer Applications， 2018， 38（5）： 1447-1452.）

[13] YIN B， WU M， WANG G H， et al. A 3.8Gb/s large-scale MIMO detector for 3GPP LTE-Advanced ［C］// Proceedings of the 2014 IEEE International Conference on Acoustics， Speech and Signal Processing. Piscataway： IEEE， 2014：3879-3883.

[14] 冯双双.基于Massive MIMO的矩阵求逆算法研究［D］.成都：电子科技大学，2016：33-51.（FENG S S. Research on matrix inversion in massive MIMO systems ［D］. Chengdu：University of Electronic Science and Technology of China， 2016： 33-51.）

[15] 杨坤，蒋林，谢晓燕，等.HEVC中率失真优化算法的动态可重构实现［J］.计算机工程与科学，2021，43（2）：354-361.（YANG K， JIANG L， XIE X Y， et al. Dynamic reconfigurable implementation of rate distortion optimization algorithm in HEVC ［J］. Computer Engineering and Science， 2021， 43（2）： 354-361.）

[16] CHEN J N， ZHANG Z B， LU H， et al. An intra-iterative interference cancellation detector for large-scale MIMO communications based on convex optimization ［J］. IEEE Transactions on Circuits amp; Systems I： Regular Papers， 2016， 63（11）： 2062-2072.

Parallel design and implementation of minimum mean square error detection algorithm based on array processor

LIU Shuai1， JIANG Lin2*， LI Yuancheng2， SHAN Rui3， ZHU Yulin4， WANG Xin4

（1.College of Communication and Information Engineering，Xi’an University of Science and Technology，Xi’an Shaanxi710054China；2.College of Computer Science and Technology，Xi’an University of Science and Technology，Xi’an Shaanxi710054，China；3.School of Electronic Engineering，Xi’an University of Posts and Telecommunications，Xi’an Shaanxi710121，China；4.College of Electrical and Control Engineering，Xi’an University of Science and Technology，Xi’an Shaanxi710054，China）

In massive Multiple-Input Multiple-Output （MIMO） systems， Minimum Mean Square Error （MMSE） detection algorithm has the problems of poor adaptability， high computational complexity and low efficiency on the reconfigurable array structure. Based on the reconfigurable array processor developed by the project team， a parallel mapping method based on MMSE algorithm was proposed. Firstly， a pipeline acceleration scheme which could be highly parallel in time and space was designed based on the relatively simple data dependency of Gram matrix calculation. Secondly， according to the relatively independent characteristic of Gram matrix calculation and matched filter calculation module in MMSE algorithm， a modular parallel mapping scheme was designed. Finally， the mapping scheme was implemented based on Xilinx Virtex-6 development board， and the statistics of its performance were performed. Experimental results show that， the proposed method achieves the acceleration ratio of 2.80， 4.04 and 5.57 in Quadrature Phase Shift Keying （QPSK）uplink with the MIMO scale of，and， respectively， and the reconfigurable array processor reduces the resource consumption by 42.6% compared with the dedicated hardware in themassive MIMO system.

massive Multiple-Input Multiple-Output (MIMO); Minimum Mean Square Error (MMSE) algorithm; parallel mapping; array processor; reconfigurable

TP302

A

1001-9081（2022）05-1524-07

10.11772/j.issn.1001-9081.2021030460

2021⁃03⁃26；

2021⁃06⁃25；

2021⁃06⁃28。

国家自然科学基金资助项目（61834005，61772417）；陕西省自然科学基金资助项目（2020JM⁃525）。

刘帅（1998—），男，陕西延安人，硕士研究生，主要研究方向：计算机体系结构； 蒋林（1970—），男，陕西杨凌人，教授，博士，主要研究方向：专用集成电路设计、计算机体系结构、计算机图形图像处理； 李远成（1981—），男，河南开封人，讲师，博士，CCF会员，主要研究方向：计算机体系结构、并行计算、机器学习； 山蕊（1986—），女，陕西咸阳人，副教授，博士，主要研究方向：集成电路设计； 朱育琳（1996—），女，陕西西安人，硕士研究生，主要研究方向：计算机体系结构； 王欣（1995—），女，陕西咸阳人，硕士研究生，主要研究方向：可重构存储结构。

This work is partially supported by National Natural Science Foundation of China （61834005， 61772417），Natural Science Foundation of Shaanxi Province （2020JM-525）.

LIU Shuai， born in 1998， M. S. candidate. His research interests include computer architecture.

JIANG Lin， born in 1970， Ph. D.， professor. His research interests include application specific integrated circuit design， computer architecture， computer graphics and image processing.

LI Yuancheng， born in 1981， Ph. D.， lecturer. His research interests include computer architecture，parallel computing， machine learning.

SHAN Rui， born in 1986， Ph. D.， associate professor. Her research interests include integrated circuit design.

ZHU Yulin， born in 1996， M. S. candidate. Her research interests include computer architecture.

WANG Xin， born in 1995， M. S. candidate. Her research interests include reconfigurable storage structure.