基于图像秘密共享的密文域可逆信息隐藏算法

王泽曦，张敏情*，柯彦，孔咏骏

（1.网络与信息安全武警部队重点实验室（武警工程大学），西安 710086； 2.武警工程大学 密码工程学院，西安 710086）（∗通信作者电子邮箱api_zmq@126.com）

基于图像秘密共享的密文域可逆信息隐藏算法

王泽曦1，2，张敏情1，2*，柯彦1，2，孔咏骏1，2

（1.网络与信息安全武警部队重点实验室（武警工程大学），西安 710086； 2.武警工程大学 密码工程学院，西安 710086）（∗通信作者电子邮箱api_zmq@126.com）

针对当前密文域可逆信息隐藏算法嵌入秘密信息后的携密密文图像的容错性与抗灾性不强，一旦遭受攻击或损坏就无法重构原始图像与提取秘密信息的问题，提出了一种基于图像秘密共享的密文域可逆信息隐藏算法，并分析了该算法在云环境下的应用场景。首先，将加密图像分割成大小相同的n份不同携密密文图像。然后，在分割的过程中将拉格朗日插值多项式中的随机量作为冗余信息，并建立秘密信息与多项式各项系数间的映射关系。最后，通过修改加密过程的内置参数，实现秘密信息的可逆嵌入。当收集k份携密密文图像时，可无损地恢复原始图像与提取秘密信息。实验结果表明，所提算法具有计算复杂度低、嵌入容量大和完全可逆等特点。在（3，4）门限方案中，所提算法的最大嵌入率可达4 bpp；在（4，4）门限方案中，其最大嵌入率可达6 bpp。所提算法充分发挥了秘密共享方案的容灾特性，在不降低秘密共享安全性的基础上，增强了携密密文图像的容错性与抗灾性，提高了算法的嵌入容量与云环境应用场景下的容灾能力，保证了载体图像与秘密信息的安全。

信息安全；图像秘密共享；可逆信息隐藏；数据容灾；密文域

0 引言

近年来，云环境下的信息安全与隐私保护要求对密文数据进行标注、检索、聚类或认证等管理，以及依托密文数据实现隐蔽通信。密文域可逆信息隐藏（Reversible Data Hiding in Encrypted Domain，RDH-ED）［1-2］作为信息隐藏技术的一个重要分支，能够实现在密文数据中嵌入秘密信息；在解密阶段，能够无误地提取秘密信息，并且无损地恢复原始数据。将密文域信息处理技术与信息隐藏技术有机融合，实现了信息加密保护与秘密信息传递的双重功效，受到了研究者们的广泛关注。

当前，密文域可逆信息隐藏算法主要分为三类：基于加密后生成冗余（Vacating Room After Encryption， VRAE）、基于加密前生成冗余（Vacating Room Before Encryption， VRBE）和基于加密过程冗余（Vacating Room In Encryption， VRIE）的密文域嵌入方案。VRAE［3］主要利用密文无损压缩或同态加密技术在密文域生成冗余，此类算法存在嵌入率不高、可分离性差等问题。Zhang［3］提出了基于流密码加密的密文域可逆信息隐藏算法，该算法通过翻转三个最低有效位嵌入1 bit信息实现信息的可逆嵌入；Zhang［4］还首次提出了可分离的密文域可逆信息隐藏算法，该算法对密文图像进行无损压缩以生成冗余，实现密文域的信息嵌入。上述算法的嵌入容量较小，Ge等［5］将图像分块加密后，在每个子块中使用直方图平移的方法进行多层嵌入，进一步提高了嵌入率，但是密钥重用会影响载体图像的安全性；顼聪等［6］在图像加密后保留块内像素高阶位平面的冗余，用像素低位替换高位的方法腾出冗余，不仅提高了嵌入容量，解密图像质量也较高。VRBE［7］主要通过加密前复杂的预处理操作生成冗余，实际应用中难以要求图像所有者执行相关操作，存在一定的应用局限，代表性的算法主要有：基于无损压缩技术［8］和基于像素预测技术［9］的RDH-ED。Puteaux等［10］基于像素值最高有效位（Most Significant Bit， MSB）预测的方法，在加密前对像素预测误差进行预处理来生成冗余空间，有效地增大了嵌入容量。VRIE［11］主要通过发掘加密过程中存在的冗余信息，利用冗余制定嵌入策略。Ke等［11-12］首次提出了基于加密过程的可逆信息隐藏方案，通过量化错误学习（Learning with Errors， LWE）加密密文空间，并利用密文扩展产生冗余嵌入秘密信息；Huang等［13］基于特殊的加密过程，在加密过程中根据像素预测误差修改密文像素以腾出空间，实现了图像的完全可逆恢复。

Chen等［14］首次提出了基于Paillier公钥密码的方法，利用乘法同态性质和直方图平移技术实现秘密嵌入；Zhang等［15］利用湿纸编码和Paillier同态特性提出了一种可分离的算法，上述算法将公钥密码与信息隐藏相结合，解决了流密码对称密钥传递与管理的难题，但是公钥密码的使用带来了较大的数据扩展，并且算法的时间复杂度较高。为了降低算法时间复杂度，减小数据扩展，Wu等［16］首次将秘密共享方案引入密文域可逆信息隐藏领域，利用差值扩展和差值直方图平移的技术，将秘密信息嵌入到共享的子秘密图像中，该方法嵌入容量较大，但是不能实现图像解密与秘密提取的可分离性，同时，也没能保留秘密共享的技术优势；Chen等［17］又提出了基于多秘密共享的方法，将像素作为多项式的系数，减小了加密的时间复杂度，但是增加了解密的时间复杂度；周能等［18］在秘密共享之前先利用差值扩展的方法预处理，再利用同态加法特性嵌入信息；Chen等［19］基于秘密共享的方法提出了两种联合、两种可分离的算法框架，扩展了RDH-ED算法的多用户场景；Ke等［20］基于中国剩余定理提出了一种可分离的RDH-ED，该方案通过组合两种嵌入方法实现了可分离性，一种是在密文域以同态差分扩展的方式嵌入，在图像重建后提取信息，另一种是在图像共享的过程中进行差分扩展，在图像重建之前提取信息。

综上所述，现有的RDH-ED算法主要利用载体图像的冗余进行秘密信息的可逆嵌入，嵌入性能受到原始载体的制约；同时，当携密密文遭受攻击或者损坏时，无法准确地提取嵌入信息和无损地恢复原始图像。针对以上问题，本文提出了一种基于Shamir图像秘密共享的密文域可逆信息隐藏算法（Secret Image Sharing-Reversible Data Hiding algorithm in Encryption Domain， SIS-RDHED），利用加密过程的冗余空间嵌入信息，嵌入性能不受载体图像的制约，在保证嵌入信息可逆提取的基础上，其嵌入容量相较文献［16］方法、文献［19］方法、文献［20］方法等同样使用秘密共享的方法得到了显著提升。同时，在不降低秘密共享方案安全性的基础上，本文算法充分利用密文分布式存储的鲁棒性，实现载体图像和嵌入信息的容灾备份。

1 基础知识

Shamir［21］提出了（k，n）门限秘密共享方案，通过构造次多项式，将秘密信息分割成多份，以保证秘密信息的安全。Thien等［22］首先将秘密共享技术应用于图像秘密共享（Secret Image Sharing， SIS），利用图像像素值替换多项式中的全部系数，实现图像的秘密分割与压缩。Shamir门限秘密共享方案是一种基于多项式的拉格朗日（Lagrange）插值问题，利用该方案构造的代数系统是基于有限域GF（q）上多项式运算的集合。

它允许用户将秘密分割成n个子秘密，每个子秘密由一个参与者持有，仅当有k个或者多于k个参与者可恢复秘密，而不足k个参与者则无法重构秘密，该方案即为Shamir（k，n）门限秘密共享。

Shamir（k，n）门限秘密共享方案一般可按如下方式构造：

步骤3 秘密恢复。由定理1知，拉格朗日插值多项式具有存在性与唯一性，即满足的阶插值多项式存在且唯一，则由任意个参与者构成的子集可以重构拉格朗日多项式，从而恢复秘密。

2 算法设计

2.1 算法框架

基于Shamir（k，n）门限图像秘密共享方案，本文提出了一种密文域可逆信息隐藏算法。该算法在秘密分割之前，将秘密信息嵌入到多项式系数中，而后生成多份携带秘密信息的子密文图像，使得密文图像与秘密信息均具有一定的容错性与抗灾性，充分发挥了秘密共享技术的优势。

本文算法框架如图1所示，首先，图像所有者将加密后的密文图像发送给信息隐藏者；然后，信息隐藏者嵌入秘密信息到多项式系数中，根据参与者的属性标签分割秘密，得到多份互不相同的携密密文图像并分发给相应的参与者；最后，接收者收集任意k份携密图像后可重构密文图像与提取秘密信息，并根据相应的密钥解密密文图像与秘密信息。表1对文中相关变量作出了说明。

表1 变量及其说明Tab. 1 Variables and their descriptions

1）参数设置。

在图像秘密共享过程中，通常选择将一个像素值作为共享的秘密，对于位深度为8 bit的图像像素，其范围为。在构建有限域时通常选择素数作为模数，将有限域中的元素限定为，当像素值为时，可直接作为多项式系数；然而，当像素值大于时，会产生溢出，即像素值为及的像素无法满足有限域的代数结构，通常对它们进行截断处理或作为边信息单独嵌入。尽管绝大多数像素值都满足代数结构，但是仍然存在边信息量过大的问题，在一定程度上直接影响了嵌入容量；同时，上述预处理操作要求在用户端完成，这在一定程度上，也限制了该类算法的应用场景。因此，选择合适的素数是至关重要的。

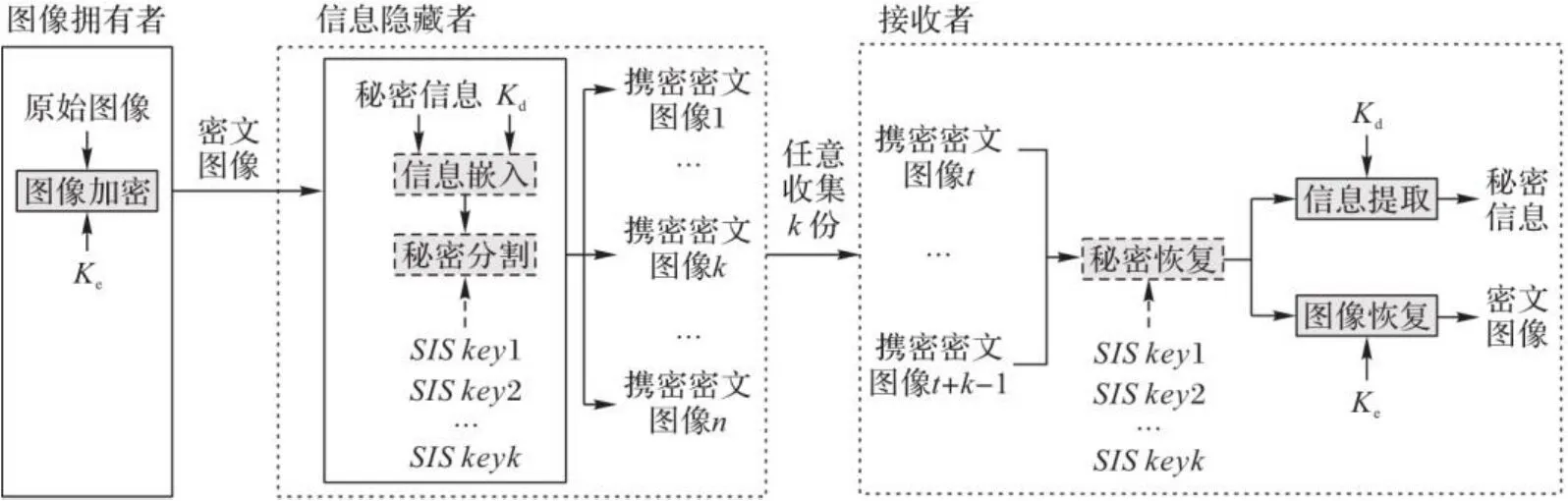
图1 SIS-RDHED框架Fig. 1 Framework of SIS-RDHED

2）图像加密。

3）信息嵌入。

步骤1 信息隐藏者选择n个参与者，并为每个参与者从有限域中选取互不相同的非零常数，作为参与者的属性标签，然后公开分发至相应的参与者。

图2 像素对合并示意图Fig. 2 Schematic diagram of pixel pair merging

4）秘密提取与图像恢复。

在Shamir（k，n）门限秘密共享方案中，秘密的恢复至少需要k个参与者完成，根据拉格朗日插值多项式的存在性及唯一性定理，由任意k个参与者构成的子集可以重构多项式，从而恢复密文图像与提取秘密信息。接收者根据不同的需求与掌握的不同密钥，可以无差错地提取秘密信息与无损地恢复密文图像。

a）图像恢复。接收者从任意k个参与者处收集k份携密密文图像，按照相同的方法对图像分块，每个分块包含一对携密密文像素，并将其合并为新的函数值，由拉格朗日插值多项式可构造如下的多项式：

由于信息嵌入方法的特殊性，使得信息提取与图像恢复的过程互不影响，均是在秘密共享恢复的过程中完成的。秘密恢复后，根据接收者掌握的不同密钥执行相关的操作，实现了算法的可分离性。

要保证方案安全且能够无误地提取秘密信息与无损地恢复原始图像，必须保证每个用户的属性标签互不相同，在提取与恢复时，必须收集足够的有效携密密文图像，证明过程如下。

为保证无误地提取秘密信息与无损地恢复原始图像，方程组必须有唯一解，即系数矩阵满秩，范德蒙德行列式不为零，因此，要求k个用户的属性标签互不相同。当参与恢复的用户少于k个时，矩阵的秩小于k，方程有无穷多解。因此，在提取与恢复时，必须收集足够的有效携密密文图像。

5）算法示例。

基于Shamir（3，4）门限秘密共享方案的SIS-RDHED流程如图3所示。首先，图像所有者将原始像素对（124，127）加密，得到密文像素对（139，232）并发送给信息隐藏者。信息隐藏者合并密文像素对后生成新的像素值35 816，从秘密信息中依次选取16 bit，加密后映射为22 320和4 520；利用秘密信息与密文像素生成多项式，根据参与者身份分割秘密，得到4组携密密文像素对（131，132）、（158，127）、（255，165）、（148，87）并发送给相应的参与者。接收者任意收集3份携密密文像素对（131，132）、（158，127）、（255，165），由拉格朗日插值多项式重构密文像素与提取秘密信息，得到秘密信息22 320和4 520，重构恢复的密文像素对为（139， 232），最后根据相应的密钥进行解密。

图3 基于Shamir（3，4）门限的SIS-RDHED流程Fig. 3 Flow chart of SIS-RDHED based on Shamir （3，4） threshold

2.2 应用框架

在基于云环境下的密文域可逆信息隐藏应用场景中，云服务器为了提高容灾能力，确保用户数据安全，通常会建立异地备份系统，而采用图像秘密共享方案不仅可以实现用户密文图像的分布式存储，提高云端数据的容灾能力，而且还能将秘密信息嵌入到用户密文图像中，实现秘密信息的安全传递。根据秘密共享的特性，当其中一个云服务器出现故障或遭受攻击时，不会影响其他云服务器对数据的恢复；同时，使得秘密信息也具有一定的容灾能力。

假设由n个云服务器参与秘密份额共享并组成共享集合，云服务器在分割用户密文图像的过程中，可以将秘密信息嵌入到多项式的系数中，最后将生成的携密密文图像分发给所有参与共享的云服务器。当部分云服务器遭受攻击或者损坏时，云服务器只需收集k份携密密文图像即可恢复用户密文图像，为合法用户提供下载服务，同时还可隐蔽地提取秘密信息。

基于Shamir（3，4）门限，探讨了SIS-RDHED在云环境下的应用场景，应用框架如图4所示。

1）图像加密阶段。

用户使用任意对称加密算法加密原始图像，然后上传密文图像至云服务器A。

2）信息嵌入阶段。

云服务器A收到用户上传的密文图像后，一方面，需要对图像进行秘密分割以实现用户数据的容灾备份；另一方面，需要嵌入秘密信息。云服务器A利用数据隐藏密钥加密秘密信息后，建立秘密信息与多项式系数的映射关系，使其与用户密文图像一同进行秘密分割，得到4份完全不同的携密密文图像，将其中3份发送至云服务器B、C、D用于数据容灾，另外一份由当前服务器保存。此时，云服务器A、B、C、D拥有完全不同的携密密文图像。

3）提取与恢复阶段。

当合法的授权用户向云服务器E发出密文图像下载的服务请求后，E可从任意3个云服务器收集3份携密密文图像，从而恢复密文图像以响应用户。同时，E根据收集的3份携密密文图像重构拉格朗日多项式，由数据隐藏密钥即可提取云服务器A嵌入的秘密信息。

在多项式中，不同系数代表不同信息，其中，常数项代表密文图像，其他各项系数代表嵌入的秘密图像，因此，图像解密与秘密信息提取是完全可分离的。

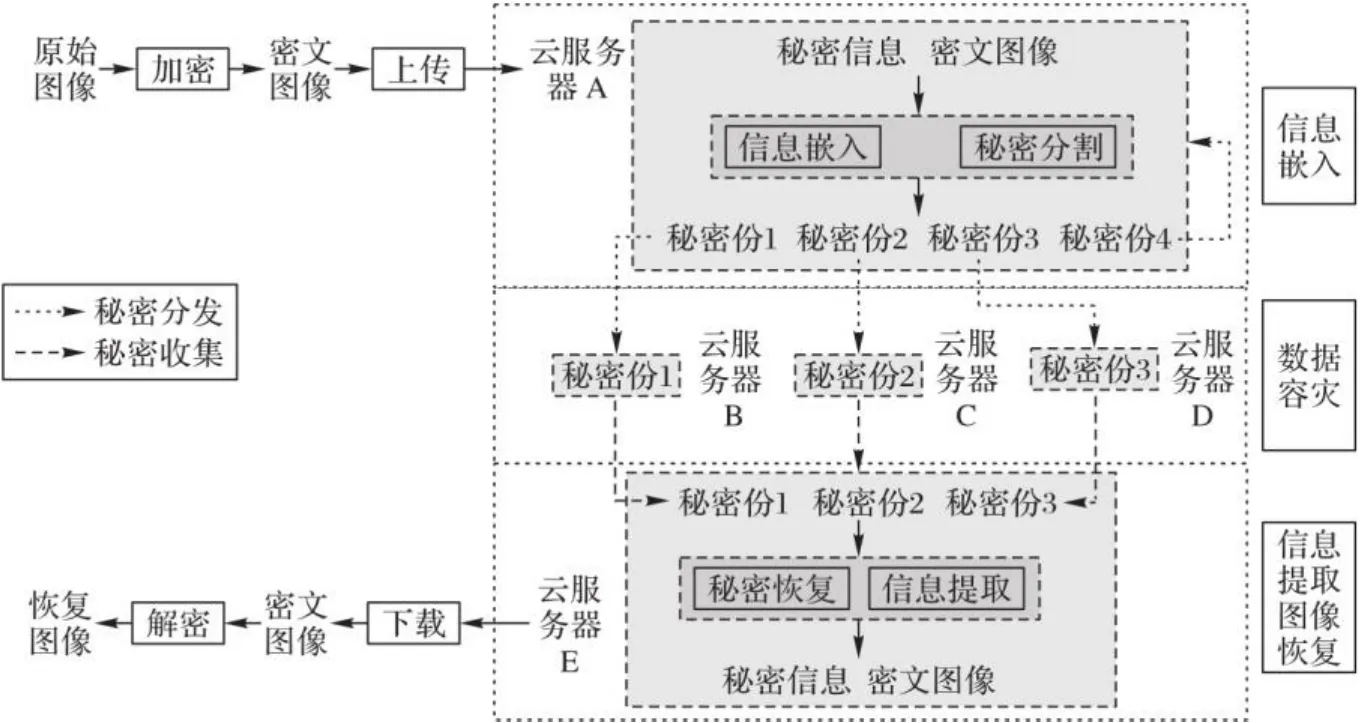
图4 基于Shamir（3， 4）门限的SIS-RDHED应用框架Fig. 4 Application framework of SIS-RDHED based on Shamir （3，4） threshold

3 实验与结果分析

图5 测试图像Fig. 5 Test images

3.1 嵌入容量

嵌入容量是评价信息隐藏算法优劣的一个重要指标。一般情况下，为直观地衡量嵌入容量，通常采用嵌入率（Embedding Rate， ER）表示，即平均每个像素所能嵌入的数据量。

秘密共享方案将秘密分割成多份，出现了密文扩展的现象，即图像在加密后会导致加密图像数据量大于原始图像的数据量，使用Shamir（3，4）门限方案加密1 bit数据，密文扩展4倍。文献［14］中使用的Paillier同态加密，密钥长度为512 bit时，加密1 bit数据密文扩展128倍。与同态加密方案相比，秘密共享的密文扩展较小，具有一定的优势。

为了避免密文扩展对信息嵌入率计算的影响，准确反映算法的实际嵌入率，文献［16］中提出了一种新的方式定义嵌入率，如式（11）所示：

在（k，n）门限方案下，对于大小为的灰度图像，根据上述定义得出算法的最大嵌入率理论值的计算方法。由式（12）可计算出不同门限参数下的最大嵌入率，并在表2中给出。

由于嵌入率与k成正比，与n成反比关系，而密文扩展与n成正比关系，在k一定的情况下，n越大嵌入率越小、密文扩展越大，这种结果并不符合预期的要求，希望嵌入率尽可能大、密文扩展尽可能小；在n一定的情况下，k越大嵌入率也越大，但是当时，不再具有容灾特性。在实际应用中，选择（3，4）、（4，5）等门限方案不仅具有容灾特性，而且算法嵌入率大、密文扩展也比较小。

表2 不同门限参数下的最大嵌入率 单位： bppTab. 2 Maximum embedding rates under different threshold parameters unit： bpp

利用加密过程中随机量替换的方式，将多项式中随机产生的高次项系数用秘密信息代替，因此，嵌入率是一个不受载体图像本身影响的恒定值。文献［3］算法将图像分为多个不重叠的块，翻转块内像素的三个最低有效位嵌入1 bit信息，嵌入率与分块大小有关；文献［6］算法是基于块内像素高位平面的冗余度来影响最大嵌入率的；文献［13］算法是在加密过程中根据预测误差进行嵌入空间的划分；文献［16］算法是根据秘密共享加密后像素差值的不变性，通过差值扩展和直方图平移嵌入信息；文献［18］算法是利用秘密共享同态性并通过差值扩展嵌入信息；文献［20］算法是基于中国剩余定理同态性与差值扩展嵌入信息。以上方法多数是根据像素的相关性腾出空间，嵌入率主要取决于载体图像；通常纹理平滑的图像具有较高的嵌入率，纹理复杂的图像嵌入率较低。

实验中利用标准测试图像对比了不同算法的最大嵌入率，如图6所示。结果表明，与其他算法相比，本文算法的最大嵌入率有明显提升。以Lena图像为例，本文算法（3，4）门限方案相较文献［10］方法提出的基于最高有效位（MSB）预测的大容量方案高出了2.99 bpp（bit per pixel），与文献［19］算法提出的（3，4）门限方案相比高出了3.0 bpp。

图6 标准测试图像不同算法的最大嵌入率对比Fig. 6 Maximum embedding rate comparison of different algorithms for standard test images

3.2 图像质量

峰值信噪比（Peak Signal-to-Noise Ratio， PSNR）是评价图像失真程度的一个重要客观指标。在密文域可逆信息隐藏算法中，除了从理论方面证明算法的可逆性外，一般还可通过计算恢复图像与原始图像的峰值信噪比来检验算法的可逆性，即恢复图像与原始图像相比无任何失真。

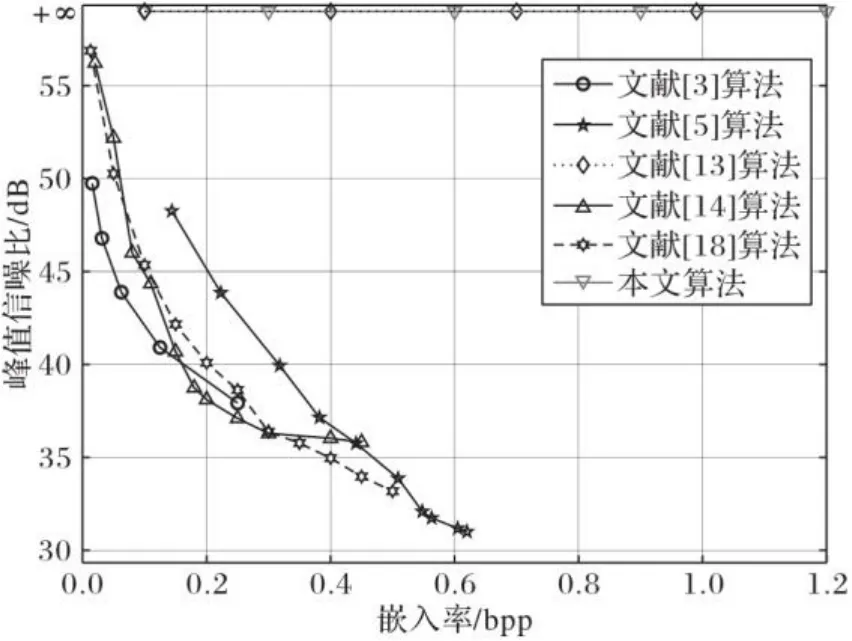
图7 Lena图像的率失真曲线对比Fig. 7 Comparison of Lena image rate distortion curve

由图7可以看出，文献［3］算法在嵌入信息时将三个最低有效位进行翻转造成了图像的失真；文献［5］算法在多层嵌入时也对图像造成了不可逆的失真；文献［14］算法和文献［18］算法通过差值扩展和同态加法特性嵌入信息，直接解密后图像存在失真。上述算法的嵌入率越大图像失真越明显，文献［13］算法在解密时利用辅助信息可以还原图像失真的部分。在本文算法中，将秘密信息嵌入到多项式的各项系数中，而载体图像作为多项式的常数项，其嵌入的信息不会影响载体图像的质量，故图像的峰值信噪比（PSNR）不随嵌入率的增加而减小。

3.3 实用性分析

3.3.1 时间复杂度

时间复杂度是指执行算法所需要的计算工作量，是评估算法优劣的重要指标。当前，密文域可逆信息隐藏算法中，常用的加密方法为流密码与公钥密码算法。表3给出了不同加密方式下算法执行的时间复杂度，具体分析如下。

表3 不同加密方式的时间复杂度Tab. 3 Time complexities of different encryption methods

在本文算法中，信息的嵌入是在秘密分割之前构造多项式的过程中通过建立秘密信息与多项式各项系数间的映射关系完成的，没有增加额外的计算次数，因此时间复杂度仍为；信息提取时需要恢复多项式的高次项系数（非常数项），利用拉格朗日插值法的过程中涉及多个因式连乘展开的情况，文献［24］中提供了一种递归算法，时间复杂度为；图像恢复时只需要恢复多项式的常数项，与秘密共享的恢复过程完全相同，时间复杂度为。

3.3.2 安全性

现有的密文域可逆信息隐藏方案，载体的保密性与秘密信息的保密性都依赖于流密码算法，即加密密钥的安全性。然而，多数信息隐藏算法在信息嵌入过程中都存在对密文图像的修改，这在一定程度上会破坏加密算法的强度与安全性。本文所提的算法，通过替换加密算法中的随机因子实现信息隐藏的目的，加密后的秘密信息与随机因子具有相同的统计特征，因此，将秘密信息嵌入到加密算法的内置参数中并不会对加密算法的安全性产生任何破坏。同时，秘密共享方案的引入，在不增加风险的情况下，增强了数据的容错性与防灾性，充分发挥了秘密共享机制的优势。

秘密恢复过程中，由于每个参与者拥有完全不同的携密密文图像，因此，至少需要个参与者提供份携密密文图像才能重构多项式，进而恢复载体图像与提取秘密信息。即使攻击者拥有份携密密文图像，载体图像与秘密信息也不会泄露。当超过个参与者提供携密密文图像时，攻击者可能伪装成合法参与者并提供无效携密密文图像，通过其他个合法参与者提供的有效携密密文图像可重构多项式。此时，攻击者仍无法获取有效信息，因为载体图像与秘密信息的安全性仍由加密密钥保证。

以Shamir（3，4）门限SIS-RDHED为例，对Lena图像仿真实验进行分析。图8给出了基于Shamir（3，4）门限SIS-RDHED的Lena图像秘密分割与重构恢复。

图8 基于Shamir（3，4）门限SIS-RDHED的Lena图像秘密分割与重构恢复Fig. 8 Secret segmentation， reconstruction and and restoration of Lena image by SIS-RDHED based on Shamir（3，4） threshold

图8中，图（a）、（b）分别为原始图像与加密后的密文图像；图（c）～（f）表示互不相同的携密密文图像，由于携密密文图像呈噪声状且直方图服从均匀分布的统计特征，攻击者无法感知秘密信息的存在；图（g）、（h）分别表示重构的密文图像与解密后无损恢复的原始图像，恢复图像的PSNR为无穷大，表明图像恢复是完全可逆的。

图9是Lena图像的重构实验直方图，其中，图（a）表示Lena原始图像直方图，图（b）、（c）分别表示不同条件下重构Lena图像的直方图。图（b）为假设攻击者已截获2份携密密文图像，并且掌握图像解密密钥的情况下，恢复出解密图像对应的直方图，表明攻击者无法获取任何与载体图像相关的信息，保证了载体图像的安全。图（c）为假设攻击者已截获3份携密密文图像，但无法获取图像解密密钥的情况下，恢复出未解密图像的直方图，表明攻击者依然无法获取任何与载体图像相关的信息，仍可保证载体图像的安全。

图10是不同数量携密密文提取秘密信息的错误图，该图是通过逐比特比较提取信息与嵌入信息是否相同绘制的错误图，其中提取信息与嵌入信息相同用0表示，否则用1表示。图（a）为使用2份携密密文提取秘密信息的错误图，图中0和1出现的概率都约为0.5，因此信息提取的错误率约为50%，即得不到任何有效信息。图（b）为使用3份携密密文提取秘密信息的错误图，图中0出现的概率为1，因此提取信息的错误率为零。

以上实验结果表明，只有在收集足够多携密密文图像的条件下，才能无误地提取秘密信息，这充分发挥了秘密共享的门限效应。

图9 基于Shamir（3，4）门限SIS-RDHED的Lena图像重构实验直方图Fig. 9 Lena image reconstruction experimental histograms by SIS-RDHED based on Shamir（3，4） threshold

图10 不同数量携密密文提取秘密信息的错误图Fig. 10 Secret data extraction error diagrams of different number of ciphertexts carrying secret

4 结语

针对传统的RDH-ED算法嵌入秘密信息后，携密密文图像的容错性与抗灾性不强的问题，本文提出了一种基于图像秘密共享的密文域可逆信息隐藏算法，通过替换加密过程中随机量的方式实现秘密信息的可逆嵌入，并分析讨论了该算法在云环境下的应用场景。通过理论分析与仿真实验可知，所提算法具有以下性能：在不降低秘密共享方案安全性的基础上，增强了载体图像与嵌入信息的容错性与抗灾性；利用加密过程的冗余空间实现信息嵌入，其嵌入性能不受载体图像的制约；实现了图像解密与秘密信息提取的完全可分离。接下来的研究方向是设计支持多用户嵌入的可逆信息隐藏算法，同时在保证较大嵌入容量的前提下，减小携密密文图像的尺寸，节约存储空间。

[1] SHI Y Q， LI X L， ZHANG X P， et al. Reversible data hiding： advances in the past two decades ［J］. IEEE Access， 2016，4： 3210-3237.

[2] 柯彦，张敏情，刘佳，等.密文域可逆信息隐藏综述［J］.计算机应用，2016，36（11）：3067-3076，3092.（KE Y， ZHANG M Q， LIU J， et al. Overview on reversible data hiding in encrypted domain ［J］. Journal of Computer Applications， 2016， 36（11）： 3067-3076， 3092.）

[3] ZHANG X P. Reversible data hiding in encrypted image ［J］. IEEE Signal Processing Letters， 2011， 18（4）： 255-258.

[4] ZHANG X P. Separable reversible data hiding in encrypted image ［J］. IEEE Transactions on Information Forensics and Security，2012， 7（2）： 826-832.

[5] GE H L， CHEN Y， QIAN Z X， et al. A high capacity multi-level approach for reversible data hiding in encrypted images ［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2019， 29（8）： 2285-2295.

[6] 顼聪，王兴田，陶永鹏.基于高阶位平面冗余的可逆信息隐藏方法［J］.计算机应用，2022，42（1）：171-177.（XU C， WANG X T， TAO Y P. Reversible data hiding method based on high-order bit-plane redundancy ［J］. Journal of Computer Applications， 2022 ，42（1）： 171-177.）

[7] MA K D， ZHANG W M， ZHAO X F， et al. Reversible data hiding in encrypted images by reserving room before encryption ［J］. IEEE Transactions on Information Forensics and Security， 2014， 8（3）： 553-562.

[8] CELIK M U， SHARMA G， TEKALP A M， et al. Lossless generalized-LSB data embedding ［J］. IEEE Transactions on Image Processing， 2005， 14（2）： 253-266.

[9] THODI D M， RODRIGUEZ J J. Prediction-error based reversible watermarking ［C］// Proceedings of the 2004 International Conference on Image Processing. Piscataway： IEEE，2004： 1549-1552.

[10] PUTEAUX P， PUECH W. An efficient MSB prediction-based method for high-capacity reversible data hiding in encrypted images ［J］. IEEE Transactions on Information Forensics and Security，2018， 13（7）： 1670-1681.

[11] KE Y， ZHANG M Q， LIU J. Separable multiple bits reversible data hiding in encrypted domain ［C］// Proceedings of the 2016 International Workshop on Digital Watermarking，LNCS 10082. Cham： Springer，2016： 470-484.

[12] 柯彦，张敏情，苏婷婷.基于R-LWE的密文域多比特可逆信息隐藏算法［J］.计算机研究与发展，2016，53（10）：2307-2322.（KE Y， ZHANG M Q， SU T T. A novel multiple bits reversible data hiding in encrypted domain based on R-LWE ［J］. Journal of Computer Research and Development， 2016， 53（10）： 2307-2322.）

[13] HUANG D L， WANG J J. High-capacity reversible data hiding in encrypted image based on specific encryption process ［J］. Signal Processing： Image Communication， 2020， 80： Article No.115632.

[14] CHEN Y C， SHIU C W， HORNG G. Encrypted signal-based reversible data hiding with public key cryptosystem ［J］. Journal of Visual Communication and Image Representation， 2014， 25（5）： 1164-1170.

[15] ZHANG X P， LONG J， WANG Z C， et al. Lossless and reversible data hiding in encrypted images with public-key cryptography ［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2016， 26（9）： 1622-1631.

[16] WU X T， WENG J， YAN W Q， et al. Adopting secret sharing for reversible data hiding in encrypted images ［J］. Signal Processing， 2018， 143： 269-281.

[17] CHEN Y C， HUNG T H， HSIEH S H， et al. A new reversible data hiding in encrypted image based on multi-secret sharing and lightweight cryptographic algorithms ［J］. IEEE Transactions on Information Forensics and Security， 2019， 14（12）： 3332-3343.

[18] 周能，张敏情，刘蒙蒙.基于秘密共享的同态加密图像可逆信息隐藏算法［J］.科学技术与工程，20（19）：7780-7786.（ZHOU N， ZHANG M Q， LIU M M. Reversible data hiding algorithm in homomorphic encrypted image based on secret sharing ［J］. Science Technology and Engineering， 2020， 20（19）： 7780-7786.）

[19] CHEN B， LU W， HUANG J W， et al. Secret sharing based reversible data hiding in encrypted images with multiple data-hiders ［J］. IEEE Transactions on Dependable and Secure Computing， 2022， 19（2）： 978-991.

[20] KE Y， ZHANG M Q， ZHANG X P， et al. Reversible data hiding scheme in encrypted domain for secret image sharing based on Chinese remainder theorem ［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2022， 32（4）： 2469-2481.

[21] SHAMIR A. How to share a secret ［J］. Communications of the ACM， 1979， 22（11）： 612-613.

[22] THIEN C C， LIN J C. Secret image sharing ［J］. Computers and Graphics， 2002， 26（5）： 765-770.

[23] 荣辉桂，莫进侠，常炳国，等.基于Shamir秘密共享的密钥分发与恢复算法［J］.通信学报，2015，36（3）：265-274.（RONG H G， MO J X， CHANG B G，et al. Key distribution and recovery algorithm based on Shamir’s secret sharing ［J］. Journal on Communications， 2015， 36（3）： 265-274.）

[24] 吴燕仙，何妮.拉格朗日插值公式的完全展开［J］.通化师范学院学报，2007，28（2）：10-12.（WU Y X， HE N. Complete expansion of Lagrange interpolation formula ［J］. Journal of Tonghua Teachers College， 2007， 28（2）： 10-12.）

Reversible data hiding algorithm in encrypted domain based on secret image sharing

WANG Zexi1，2， ZHANG Minqing1，2*， KE Yan1，2， KONG Yongjun1，2

（1.Key Laboratory of PAP for Cryptology and Information Security（Engineering University of PAP），Xi’an Shaanxi710086，China；2.College of Cryptographic Engineering，Engineering University of PAP，Xi’an Shaanxi710086，China）

The current reversible data hiding algorithms in encrypted domain have the problems that the ciphertext images carrying secret have poor fault tolerance and disaster resistance after embedding secret data， once attacked or damaged， the original image cannot be reconstructed and the secret data cannot be extracted. In order to solve the problems， a new reversible data hiding algorithm in encrypted domain based on secret image sharing was proposed， and its application scenarios in cloud environment were analyzed. Firstly， the encrypted image was divided intondifferent ciphertext images carrying secret with the same size. Secondly， in the process of segmentation， the random quantities in Lagrange interpolation polynomial were taken as redundant information， and the mapping relationship between secret data and each polynomial coefficient was established. Finally， the reversible embedding of the secret data was realized by modifying the built-in parameters of the encryption process. Whenkciphertext images carrying secret were collected， the original image was able to be fully recovered and the secret data was able to be extracted. Experimental results show that， the proposed algorithm has the advantages of low computational complexity， large embedding capacity and complete reversibility. In the （3，4） threshold scheme， the maximum embedding rate of the proposed algorithm is 4 bit per pixel （bpp）， and in the （4，4） threshold scheme， the maximum embedding rate of the proposed algorithm is 6 bpp. The proposed algorithm gives full play to the disaster recovery characteristic of secret sharing scheme. Without reducing the security of secret sharing， the proposed algorithm enhances the fault tolerance and disaster resistance of ciphertext images carrying secret， improves the embedding capacity of algorithm and the disaster recovery ability in the application scenario of cloud environment， and ensures the security of carrier image and secret data.

information security; secret image sharing; reversible data hiding; data disaster recovery; encrypted domain

TP309.7

A

1001-9081（2022）05-1480-10

10.11772/j.issn.1001-9081.2021050823

2021⁃05⁃19；

2021⁃09⁃22；

2021⁃10⁃14。

国家自然科学基金资助项目（61872384）。

王泽曦（1997—），男，江苏徐州人，硕士研究生，主要研究方向：信息安全、信息隐藏； 张敏情（1967—），女，陕西西安人，教授，博士，主要研究方向：密码学、信息隐藏； 柯彦（1991—），男，河南南阳人，博士，主要研究方向： 信息安全、密码学、信息隐藏； 孔咏骏（1990—），男，江苏江阴人，博士研究生，主要研究方向：信息安全、信息隐藏。

This work is partially supported by National Natural Science Foundation of China （61872384）.

WANG Zexi， born in 1997， M. S. candidate. His research interests include information security，data hiding.

ZHANG Minqing， born in 1967， Ph. D.， professor. Her research interests include cryptology， data hiding.

KE Yan， born in 1991， Ph. D. His research interests include information security， cryptology， data hiding.

KONG Yongjun， born in 1990， Ph. D. candidate. His research interests include information security，data hiding.