基于自适应近邻参数的密度峰聚类算法

周欢欢，郑伯川，张征，张琦

（1.西华师范大学 数学与信息学院，四川 南充 637009； 2.西华师范大学 计算机学院，四川 南充 637009）（∗通信作者电子邮箱zhengbc@vip.163.com）

基于自适应近邻参数的密度峰聚类算法

周欢欢1，郑伯川2*，张征1，张琦1

（1.西华师范大学 数学与信息学院，四川 南充 637009； 2.西华师范大学 计算机学院，四川 南充 637009）（∗通信作者电子邮箱zhengbc@vip.163.com）

针对基于共享最近邻的密度峰聚类算法中的近邻参数需要人为设定的问题，提出了一种基于自适应近邻参数的密度峰聚类算法。首先，利用所提出的近邻参数搜索算法自动获得近邻参数；然后，通过决策图选取聚类中心；最后，根据所提出的代表点分配策略，先分配代表点，后分配非代表点，从而实现所有样本点的聚类。将所提出的算法与基于共享最近邻的快速密度峰搜索聚类（SNN‑DPC）、基于密度峰值的聚类（DPC）、近邻传播聚类（AP）、对点排序来确定聚类结构（OPTICS）、基于密度的噪声应用空间聚类（DBSCAN）和K-means这6种算法在合成数据集以及UCI数据集上进行聚类结果对比。实验结果表明，所提出的算法在调整互信息（AMI）、调整兰德系数（ARI）和FM指数（FMI）等评价指标上整体优于其他6种算法。所提算法能自动获得有效的近邻参数，且能较好地分配簇边缘区域的样本点。

共享最近邻；局部密度；密度峰聚类；-近邻；逆近邻

0 引言

聚类分析是在无任何先验知识的条件下，对一组对象进行处理，根据数据对象或者物理对象的相似度将对象划分为多个类簇，使得类间相似度尽可能小、类内相似度尽可能大。聚类分析已经被广泛应用在于统计学、生物学、医学、模式识别、信息检索、人工智能和图像处理等领域。

聚类分析是数据挖掘研究中的一个活跃领域。针对不同类型的应用程序，研究者们相继提出了一系列的聚类算法。典型的聚类算法包括：基于划分的K-means和K-medoids，基于层次的利用代表点聚类（Clustering Using REpresentative， CURE）算法和平衡迭代规约层次聚类（Balanced Iterative Reducing and Clustering using Hierarchies，BIRCH），基于密度的噪声应用空间聚类（Density-Based Spatial Clustering of Applications with Noise， DBSCAN）［5］和对点排序来确定聚类结构（Ordering Points To Identify the Clustering Structure， OPTICS），基于网格的小波变换聚类算法（WaveCluster）和统计信息网格方法（STatistical INformation Grid-based method， STING），基于模型的统计聚类［1］和基于图论的光谱聚类［2］。近年来，随着聚类分析的发展，一些新的聚类算法被提出，如子空间聚类［3］、集成聚类［4］和深度嵌入聚类［5］。聚类算法的种类繁多，算法的性能也各不相同。

K-means是经典的聚类算法，具有良好的聚类性能，但是也存在一些不足。K-means需要大量计算样本点到聚类中心的距离，时间复杂度高，影响计算速度。Xia等［6］提出了一种无边界的快速自适应聚类算法减少距离计算；Taylor等［7］则通过GPU运行K-means算法。这些改进算法能有效提高K-means算法的运行速度。另外，K-means算法在凸球形结构的数据集上能取得很好的聚类结果，但是对有任意形状的簇的数据集，容易陷入局部最优，聚类效果不理想。DBSCAN算法对类簇的形状不敏感，抗噪能力强，但是对于密度不均匀和高维数据，聚类效果不理想［8-9］。此外，DBSCAN算法对于半径和阈值的选择也是一个难点。Rodriguez等［10］提出了基于密度峰值的聚类（Clustering by fast search and find of Density Peaks， DPC）算法。与K-means、DBSCAN、OPTICS等传统算法相比，DPC算法具有简单高效、无需迭代目标函数、能准确找到聚类中心、适应于任意形状的数据集等优点。由于DPC算法具有较多优点，使其在短时间内被广泛应用于计算机视觉［11］、图像识别［12］、文本挖掘［13］等领域。然而，DPC算法存在以下不足：1）聚类结果对截断距离敏感；2）局部密度和距离测量的定义过于简单，导致无法处理多尺度、密度不均衡和其他复杂特征的数据集；3）非聚类中心分配策略容错能力差。

近年来，许多学者针对DPC算法存在的不足，对其进行了改进尝试［14-18］。Du等［14］提出了基于K-近邻的密度峰聚类（Density Peaks Clustering based onK-Nearest Neighbors，KNN-DPC）算法，解决了DPC算法只考虑数据集全局结构的问题，为计算局部密度提供了另一种选择。Guo等［16］提出了新的密度峰聚类算法（New local density for Density Peak Clustering，NDPC），NDPC算法在DPC算法中加入了逆近邻，将局部密度改为数据点的逆近邻个数，根据每个点的逆近邻数来确定聚类中心。该算法的度量方式能有效地解决DPC算法的密度不均衡问题。钱雪忠等［19］提出了自适应聚合策略优化的密度峰值聚类算法，通过类簇间密度可达来合并相似类簇，不需要输入簇数，但是需要输入近邻参数。Liu等［20］提出了一种基于共享最近邻的快速密度峰搜索聚类（Shared-Nearest-Neighbor-based Clustering by fast search and find of Density Peaks，SNN‑DPC）算法，该算法提出了基于共享近邻的局部密度度量方式和与最近的较大密度点距离的自适应度量方式。SNN-DPC算法能处理多尺度、交叉缠绕、密度不均衡和较高维复杂的数据集，并且样本被错误分配时不会导致进一步的错误。

2）提出了代表点的概念，并基于该概念提出了新的非聚类中心分配策略，避免数据点被错误分配时导致进一步的错误。

1 DPC算法及SNN‑DPC算法

1.1 DPC算法

DPC是一种基于密度和距离的聚类算法。该算法基于以下假设：聚类中心被具有较低局部密度的邻居包围，并且不同聚类中心之间的距离相对较远。DPC算法有两个重要指标来描述每个样本点：样本的局部密度和样本到距离最近且局部密度较大样本点的距离。

DPC算法通过决策图选取理想的聚类中心，所谓理想的聚类中心是指距离较远且密度较高的样本点，即选择较大的决策值对应的样本点为聚类中心。

根据文献［18］可知，DPC算法分为两个步骤：1）通过计算每个点的和，得到决策图，然后从决策图中选择决策值较高的点作为聚类中心。2）将剩余的点分配给距其最近且具有较高密度的点所在的簇。

通过DPC算法获得的实验结果表明，在许多情况下处理数据集都能得到很好的聚类结果，但是它的缺点也显而易见，比如：1）聚类结果对参数敏感。2）对于密度不均衡数据，错误选择聚类中心，导致聚类结果不理想，如图1所示的经典Jain数据集。3）非聚类中心的分配策略敏感，容错能力差，如图2所示的Pathbased数据集。

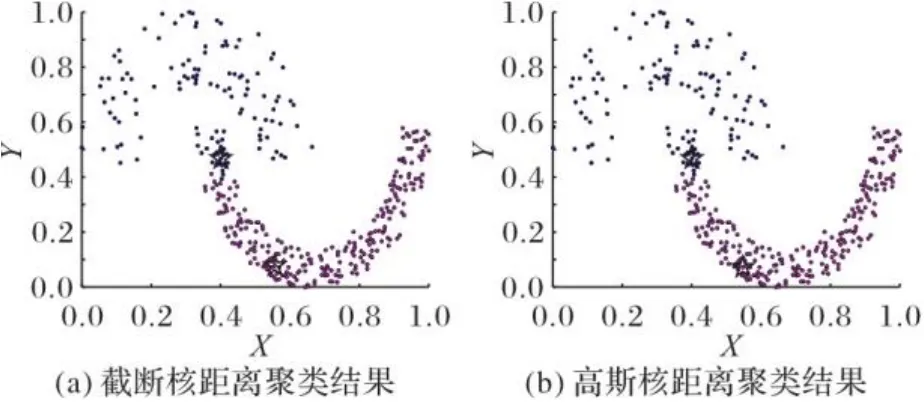
图1 Jain数据集聚类结果Fig. 1 Clustering results of Jain dataset

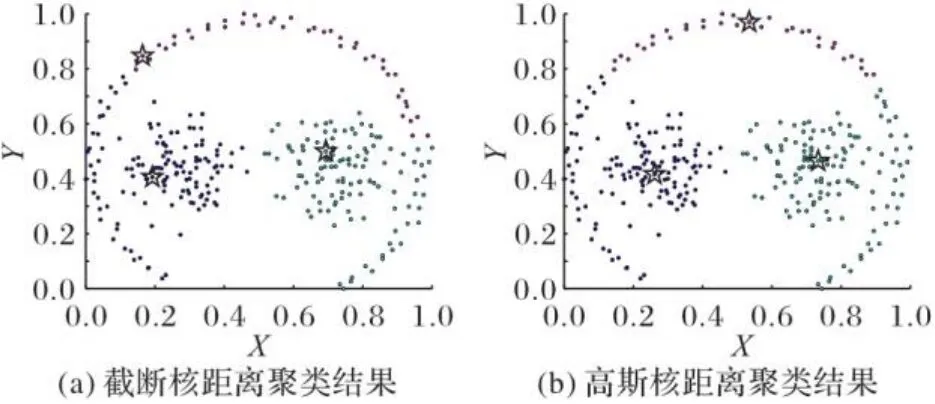
图2 Pathbased数据集聚类结果Fig. 2 Clustering results of Pathbased dataset

针对DPC算法存在的上述问题，文献［20］中提出了一种基于共享近邻的密度峰快速搜索算法SNN-DPC。

1.2 SNN-DPC算法

由于DPC算法直接计算样本点之间的距离和密度，没有关注样本点所在的环境，所以DPC算法在某些复杂的数据集上无法产生令人满意的结果。理论上样本点的大多数邻居应该属于同一个簇，据此引入了共享近邻SNN的概念来描述样本点的局部密度和样本点之间的距离，考虑到了每个点受周围邻居的影响。

SNN的基本思想为：若两个样本点共享的邻居总数之和越大，则它们被认为更相似。下面详细介绍SNN-DPC相关定义。

定义2 逆近邻［22］。假设样本点，样本点在样本点的-近邻集中，则称样本点为点的逆近邻，表达式如下：

在SNN-DPC算法中，首先根据决策图确定聚类中心，然后分配满足式（11）的必然从属点，最后分配满足式（12）的可能从属点。

未分配的点不符合必然从属点，则将其定义为可能从属点，表达式如下：

1.3 SNN-DPC算法分析

SNN-DPC算法引入了共享近邻的概念［23］，改进了局部密度和距最近密度较大点的距离的定义，能反映数据集的局部特征，进而可以反映数据的自然结构；因此该算法能处理交叉缠绕、不同密度和高维度的复杂数据集，抗噪能力强，同时保留了DPC算法的大多数优点。对于非聚类中心采用两步分配方法，避免数据点被错误分配时出现进一步错误。在SNN-DPC算法中，通过值来确定每个样本点的邻域，它影响着算法过程中的关键步骤。换言之，近邻参数直接决定SNN-DPC算法的性能。然而，SNN-DPC算法需要人工确定近邻参数。因此，本文提出了基于自适应近邻参数的密度峰聚类算法，可以有效解决近邻参数的设定问题。

2 基于自适应近邻参数的密度峰聚类算法

2.1 近邻参数搜索算法

样本点之间的相关程度不仅与近邻有关，还与逆近邻有关。数据集密集区域的样本点具有较多的互为近邻的点，稀疏区域的样本点有相对较少的互为近邻的点。因此，每个样本的互为近邻数能反映数据集局部分布情况。当最离群的样本点都有互为近邻的点时，数据集中所有点都应该有互为近邻点。基于这一假设，本文提出了一种近邻参数搜索算法，用于自动获得近邻参数值。

5） endwhile

2.2 分配策略

定义10 代表点。如果满足式（13）则称该点为代表点。

由于样本点的逆近邻数不会受数据集密度不均衡的影响，能更准确地反映数据集的分布特征。以Aggregation数据集为例，图3（a）为所有点分布图，图3（b）为代表点分布图。如图3所示，具有少量逆近邻的样本点普遍分布在数据集每个簇的边缘，代表点具有相对较多的逆近邻数，所以代表点通常不会出现在数据集每个簇的边缘。因此本文提出了以逆近邻数为主的非聚类中心两步分配策略。该策略先将代表点分配给相应的簇，最后分配非代表点。通过近邻参数搜索算法得到的近邻参数，能选出数据集相对集中区域的样本点作为代表点。

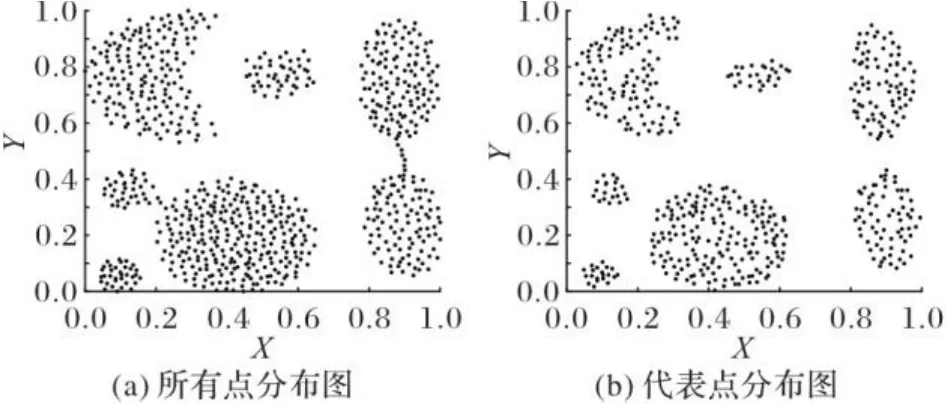
图3 原始样本点和代表点分布情况Fig. 3 Distribution of original sample points and representative points

2.3 算法流程

算法2 基于自适应近邻参数的密度峰聚类算法。

输出 聚类结果。

2）计算距离矩阵；

3）根据式（8）计算相似矩阵；

5）根据式（10）计算样本点与距离最近且密度较大的样本点之间的距离；

9）利用算法3分配代表点；

10）利用算法4分配非代表点。

算法2中利用算法3分配代表点，利用算法4分配非代表点，它们的具体实现如下。

算法3 代表点分配算法。

1）使用式（13）计算得到所有代表点。

b） 如果该近邻点是代表点且不属于任何簇，则将其分配到头部点所在的簇，同时，如果该近邻点和头部点的共享近邻数大于等于，则将该近邻点添加到队列的尾部；

算法4 非代表点分配算法。

5）循环步骤1）～4），直至非代表点分配完。

3 实验与结果分析

3.1 实验环境及评价指标

本文算法采用Matlab 2018a实现，硬件配置为Windows 10操作系统，8 GB物理内存，硬件环境为Intel Xeon CPU E3-1240 v5@3.50 GHz。

为验证本文算法的有效性，分别在经典的合成数据集和UCI真实数据集上进行聚类实验。实验中，以SNN‑DPC［20］、DPC［10］、DBSCAN、OPTICS、近邻传播聚类（Affinity Propagation， AP）［24］和K-means作为对照比较算法。所有对比算法都是针对已知簇数的情况下进行聚类，除了簇数外不同的方法需要设置不同的参数：本文算法不需要其他参数；SNN‑DPC算法需要一个参数（每个样本点的邻居数量）；DPC算法需要参数：（截断距离）；DBSCAN和OPTICS算法需要两个参数：（邻域半径）和（邻域半径内期望样本个数），前者是浮点数，后者是整数；AP算法有一个参数：偏好参数（样本点作为聚类中心的参考度）；K-means算法直接采用已知的簇数。实验聚类结果中的参数值是各算法取得最佳结果时的参数值。由于所有算法采用已知簇数，因此没有给出具体簇数参数。实验中采用调整互信息（Adjusted Mutual Information， AMI）［25］、调整兰德系数（Adjusted Rand Index， ARI）［25］和FM指数（Fowlkes and Mallows Index， FMI）［26］这三种评价指标对聚类结果进行评价。AMI用于计算聚类结果与真实分类的相似性，取值范围为，该值越接近1表示聚类结果越好，反之则聚类效果越差。ARI衡量聚类结果与真实分类的吻合程度，取值范围为［-1，1］，该值越接近1表示聚类结果越准确，反之则聚类结果越差。FMI计算聚类结果与真实值得到精确率和召回率的几何平均数，取值范围为［0，1］，该值越接近1表示聚类结果越接近真实值，反之则聚类的质量越差。在进行实验之前，需对数据进行预处理，采用最小最大归一化方法将数据每维都归一化到［0，1］，从而消除维度差异的影响。

3.2 结果分析

选取8个经典的合成数据集和4个UCI真实数据集进行实验，所选数据集在聚类总体分布和属性以及数量方面有所不同。因此，所选数据集能更好地比较各种聚类算法的性能。数据详细信息如表1～2所示。

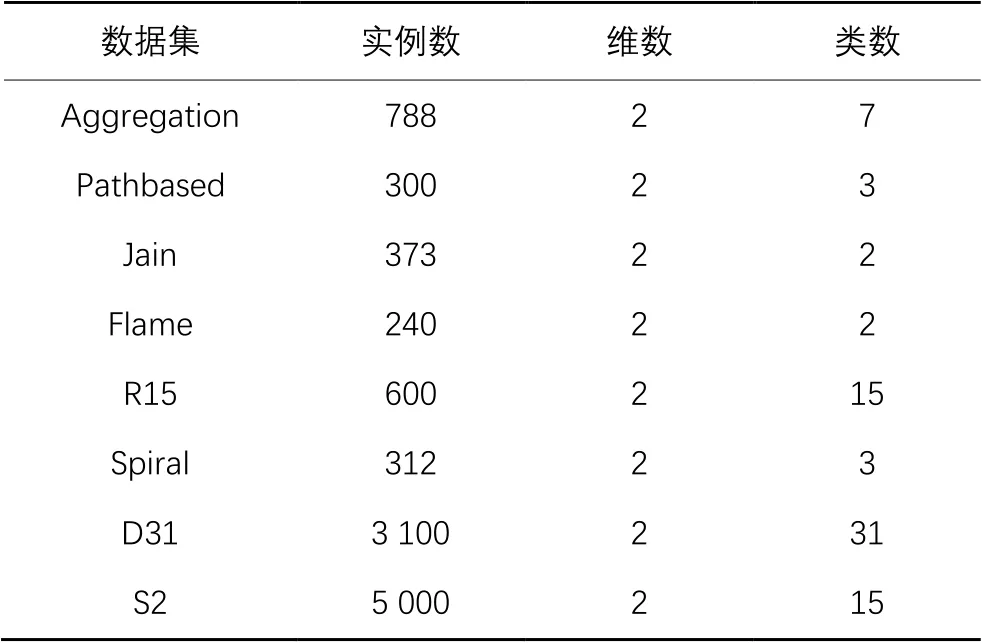
表1 合成数据集信息Tab. 1 Synthetic dataset information

表2 UCI数据集信息Tab. 2 UCI dataset information

图4～11为8个合成数据集的原始聚类图和本文算法获得的聚类效果图，其中具有不同颜色的点被分配给不同的簇，聚类中心以星号表示。从图4～11中可以看出，本文聚类算法在各种形状的数据集上都能准确找到聚类中心，能较准确地对每个样本点划分簇，而且对螺旋型和密度不均衡数据集也能正确聚类；另外也可以看出，代表点分配策略对簇边缘区域样本点聚类效果比较理想。

为了验证本文算法的聚类效果，以AMI、ARI和FMI为评价指标判断其聚类效果。实验中分别记录了本文算法、SNN-DPC算法、DPC算法、DBSCAN算法、OPTICS算法、AP算法和K-means算法在8个合成数据集和4个UCI真实数据集上的AMI、ARI和FMI值，结果如表3～4所示。表3～4中，除了本文算法和SNN‑DPC算法的实验结果外，其他算法的实验结果来自于文献［20］。

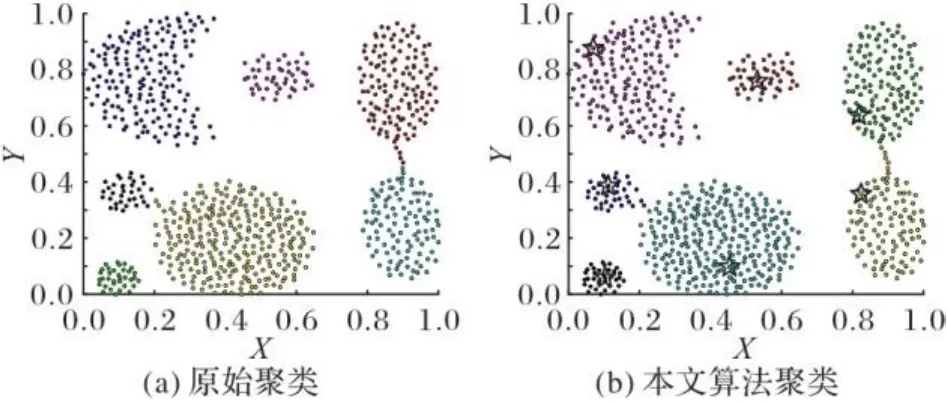
图4 Aggregation数据集聚类效果Fig. 4 Clustering effect of Aggregation dataset

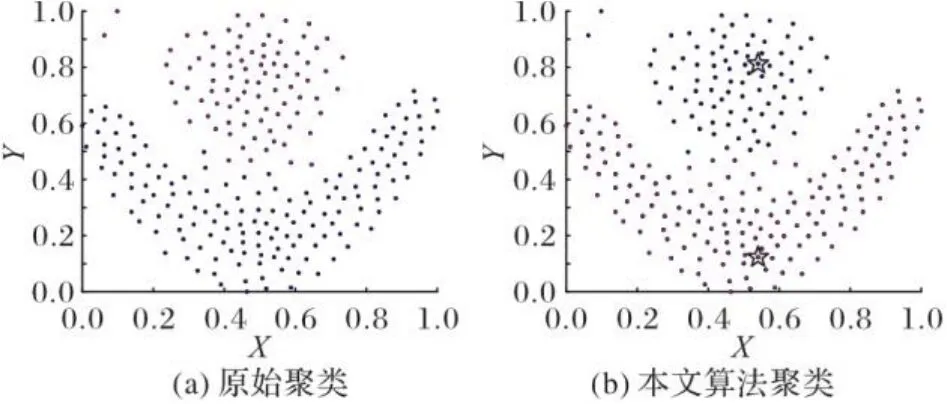
图5 Flame数据集聚类效果Fig. 5 Clustering effect of Flame dataset

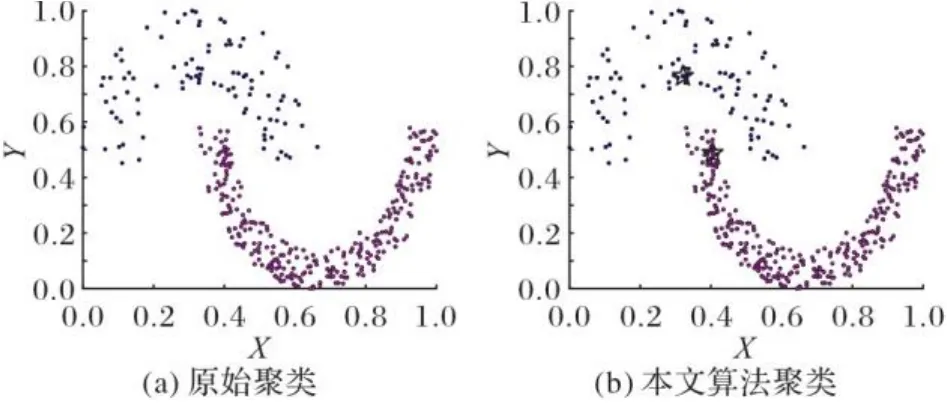
图6 Jain数据集聚类效果Fig. 6 Clustering effect of Jain dataset

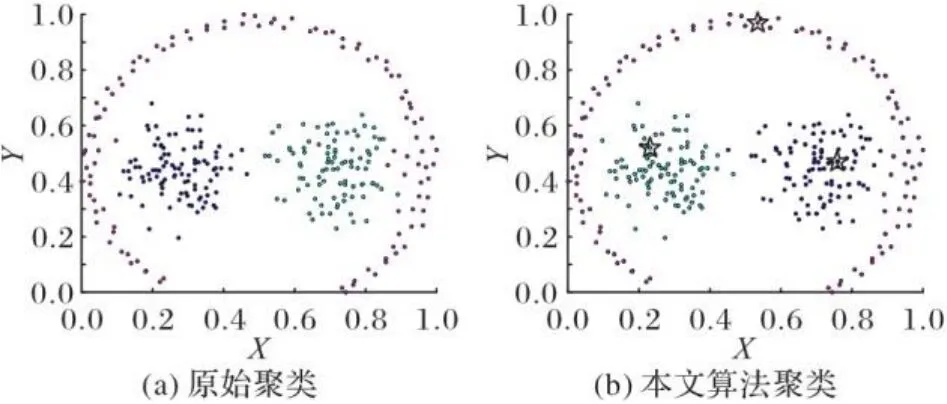
图7 Pathbased数据集聚类效果Fig. 7 Clustering effect of Pathbased dataset

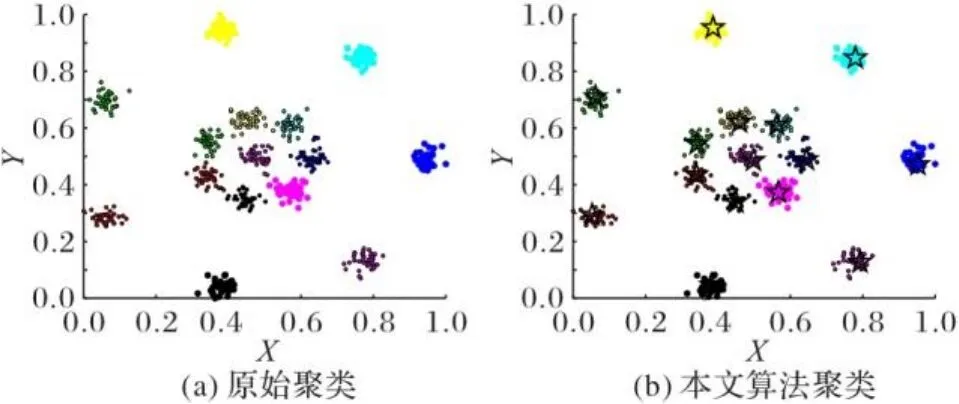
图8 R15数据集聚类效果Fig. 8 Clustering effect of R15 dataset

表3是在合成数据集上的实验结果，除了Flame数据集和D31数据集，本文算法的AMI、ARI和FMI指标在合成数据集上都优于或等于SNN-DPC算法。其中，对于Aggregation数据集，本文算法的AMI、ARI和FMI指标相较SNN-DPC算法分别提高了2.94个百分点、2.61个百分点和2.05个百分点；对于Pathbased数据集，本文算法的AMI、ARI和FMI指标相较SNN-DPC算法分别提高了1.85个百分点、3.92个百分点和1.38个百分点。如表4所示，本文算法的3个指标在UCI数据集上优于或等于SNN-DPC算法，其中对于Seeds数据集，本文算法的AMI、ARI和FMI指标相较SNN-DPC算法分别提高了24.91个百分点、21.1个百分点和17.24个百分点。因此，本文算法通过自动计算近邻参数和分配策略达到甚至超过了SNN‑DPC算法的聚类性能，克服了SNN‑DPC算法需要人工设置参数的不足。

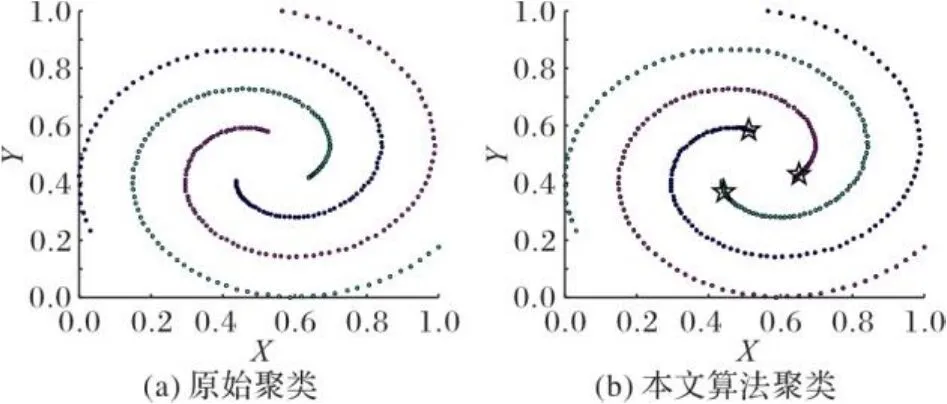
图9 Spiral数据集聚类效果Fig. 9 Clustering effect of Spiral dataset

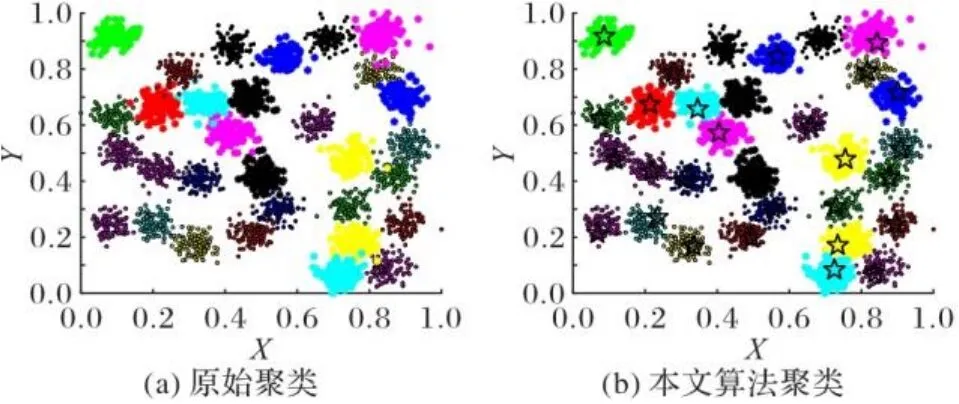
图10 D31数据集聚类效果Fig. 10 Clustering effect of D31 dataset

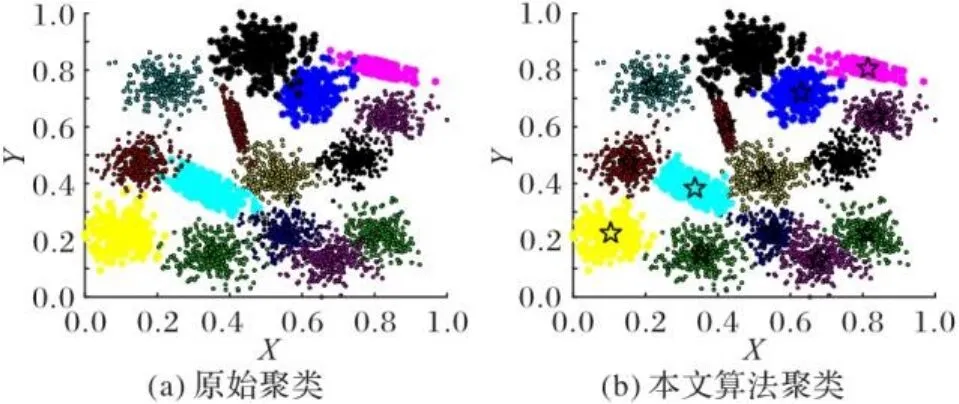
图11 S2数据集聚类效果Fig. 11 Clustering effect of S2 dataset

另外，对于表3的合成数据集，除了在Aggregation数据集和Flame数据集上本文算法的3个评价指标略低于DPC，在S2数据集上本文算法的3个指标略低于K-means算法外，本文算法的指标在其他数据集上都优于DPC、DBSCAN、OPTICS、AP和K-means算法。对于表4的真实数据集，在Wine和Seeds数据集上，本文算法的3个评价指标都等于或者超过其他算法；在Blance Scale数据集上，DPC算法的3个指标都优于其他算法，本文算法的3个指标只优于SNN-DPC；在Segmentation数据集上，本文算法的3个指标只略低于DPC算法，但优于其他算法。

表3 不同算法在合成数据集上的聚类结果Tab. 3 Clustering results of different algorithms on synthetic datasets

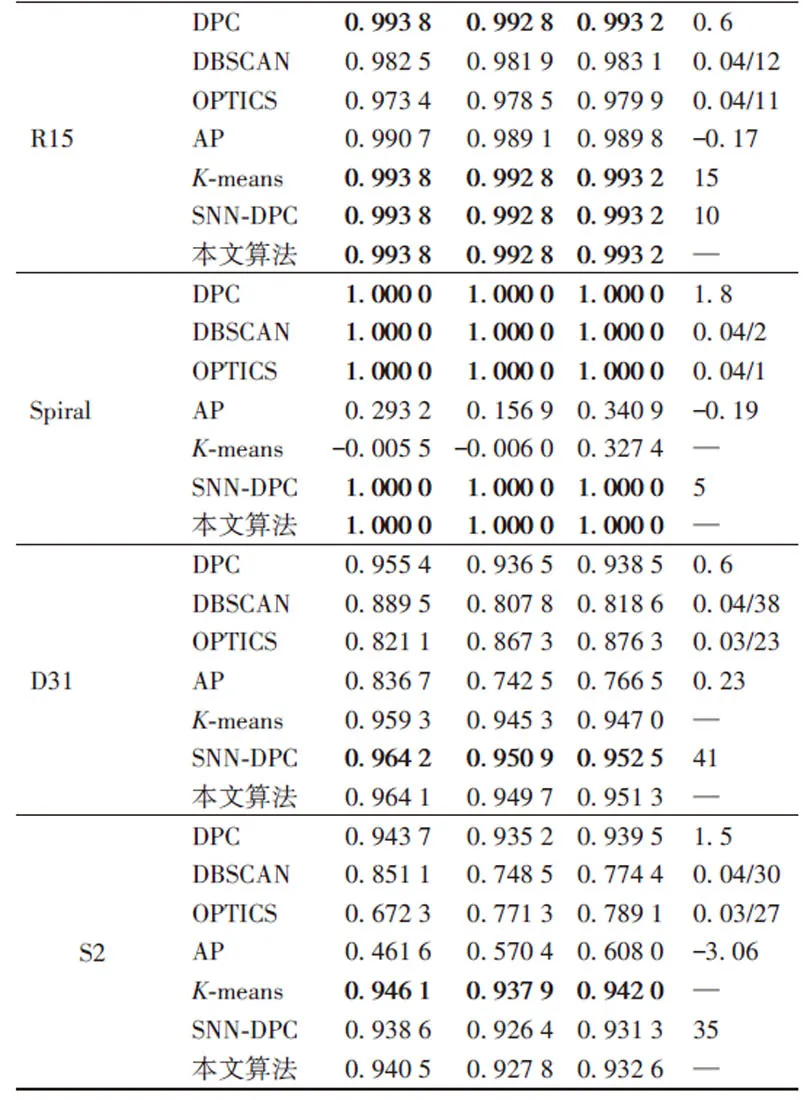
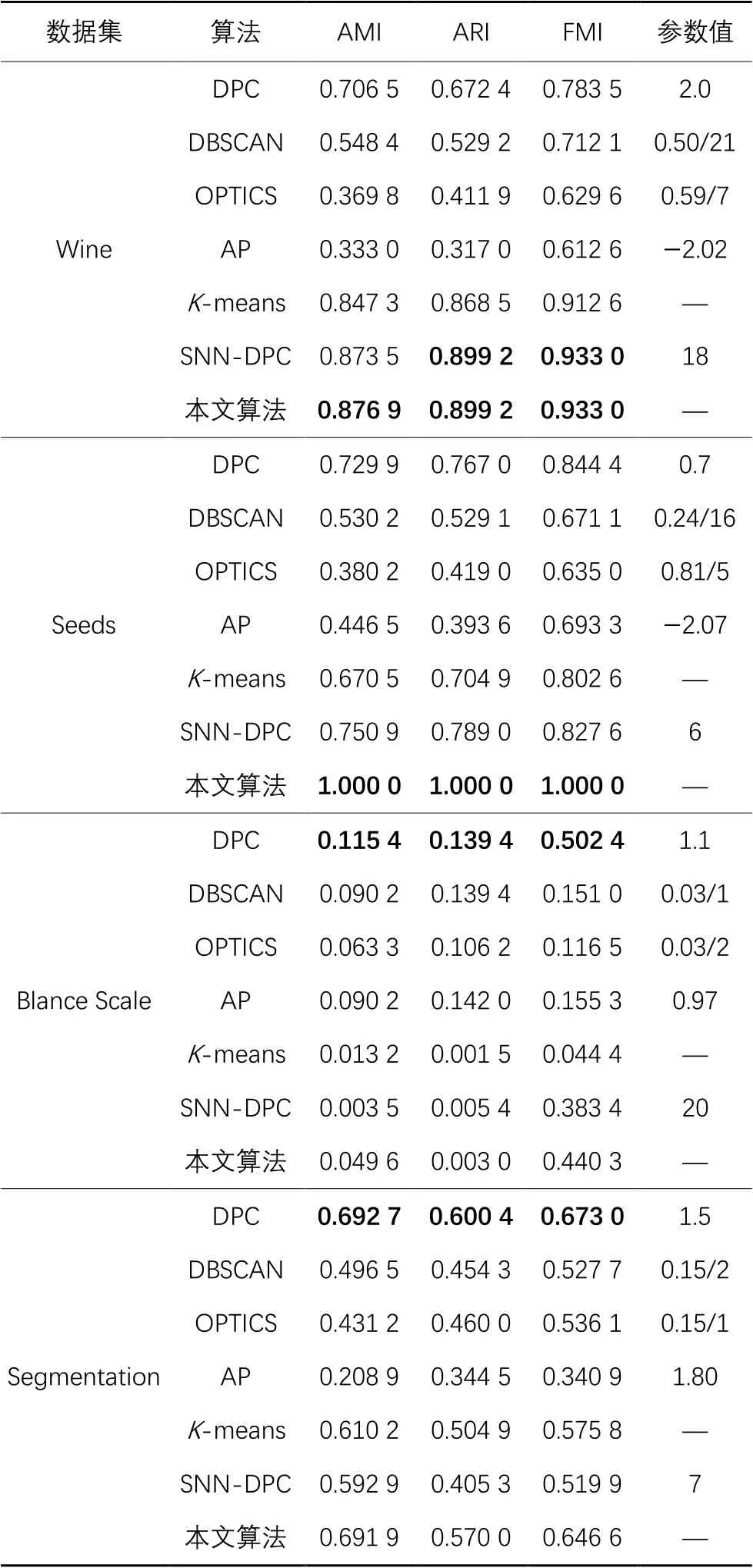
表4 不同算法在UCI数据集上的聚类结果Tab. 4 Clustering results of different algorithms on UCI datasets

综上，可以看出，本文算法的整体聚类性能较好，只在个别数据集上略低于其他算法，这可能与数据集的特征有关系，比如，在Blance Scale数据集上，所有对比算法的3个评价指标都较低。另外，在几个数据集上DPC算法的指标比本文算法好，其原因可能是：DPC算法通过人工逐一测试出最佳参数，而本文算法是自动计算出来的参数k。因此，从算法通用性上来讲，本文算法优于DPC算法。

4 结语

在经典合成数据集和UCI数据集上的实验结果表明，所提算法不仅保留了SNN-DPC算法能准确找到聚类中心、抗噪能力强、能处理分布不均和任意形状的数据集等优点，还可以自适应确定近邻参数，此外，该算法还可以较好地分配簇边缘区域的样本点。实验结果表明，所提基于自适应近邻参数的密度峰聚类算法是一种有效的自适应聚类算法，能自适应得到近邻参数。然而，在无先验知识的情况下，如何确定算法中数据集的簇数需要进一步的研究。

[1] DEMPSTER A P， LAIRD N M， RUBIN D B. Maximum likelihood from incomplete data via the EM algorithm ［J］. Journal of the Royal Statistical Society： Series B （Methodological）， 1977， 39 （1）： 1-22.

[2] LUXBURG U von. A tutorial on spectral clustering ［J］. Statistics and Computing， 2007， 17（4）： 395-416.

[3] AGRAWAL R， GEHRKE J， GUNOPULOS D， et al. Automatic subspace clustering of high dimensional data for data mining applications ［C］// Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data. New York： ACM， 1998： 94-105.

[4] STREHL A， GHOSH J. Cluster ensembles — a knowledge reuse framework for combining multiple partitions ［J］. Journal of Machine Learning Research， 2002， 3： 583-617.

[5] XIE J Y， GIRSHICK R， FARHADI A. Unsupervised deep embedding for clustering analysis ［C］// Proceedings of the 2016 33rd International Conference on International Conference on Machine Learning. New York： JMLR.org， 2016： 478-487.

[6] XIA S Y， PENG D W， MENG D Y， et al. Ballk-means： fast adaptive clustering with no bounds ［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2022， 44（1）： 87-99.

[7] TAYLOR C， GOWANLOCK M. Accelerating the Yinyangk-means algorithm using the GPU ［C］// Proceedings of the 2021 IEEE 37th International Conference on Data Engineering. Piscataway： IEEE， 2021：1835-1840.

[8] TAN P N， STEINBACK M， KARPATNE A， et al. Introduction to Data Mining ［M］. 2nd ed. London： Pearson， 2019：565-570.

[9] XIE J Y， GAO H C， XIE W X， et al. Robust clustering by detecting density peaks and assigning points based on fuzzy weightedK-nearest neighbors ［J］. Information Sciences， 2016， 354：19-40.

[10] RODRIGUEZ A， LAIO A. Clustering by fast search and find of density peaks ［J］. Science， 2014， 344（6191）： 1492-1496.

[11] SHI Y， CHEN Z S， QI Z Q， et al. A novel clustering-based image segmentation via density peaks algorithm with mid-level feature ［J］. Neural Computing and Applications， 2017， 28（S1）： 29-39.

[12] CHEN Y W， LAI D H， QI H， et al. A new method to estimate ages of facial image for large database ［J］. Multimedia Tools and Applications， 2016， 75（5）： 2877-2895.

[13] ZHANG Y， XIA Y Q， LIU Y， et al. Clustering sentences with density peaks for multi-document summarization ［C］// Proceedings of the 2015 Conference of the North American Chapter of the Association for Computational Linguistics： Human Language Technologies. Stroudsburg： Association for Computational Linguistics， 2015： 1262-1267.

[14] DU M J， DING S F， JIA H J. Study on density peaks clustering based onk-nearest neighbors and principal component analysis ［J］. Knowledge-Based Systems， 2016， 99： 135-145.

[15] 鲍舒婷，孙丽萍，郑孝遥，等.基于共享近邻相似度的密度峰聚类算法［J］.计算机应用，2018，38（6）：1601-1607.（BAO S T， SUN L P，ZHENG X Y， et al. Density peaks clustering algorithm based on shared near neighbors similarity ［J］. Journal of Computer Applications， 2018， 38（6）： 1601-1607.）

[16] GUO Z S， HUANG T Y， CAI Z L， et al. A new local density for density peak clustering ［C］// Proceedings of the 2018 Pacific-Asia Conference on Knowledge Discovery and Data Mining， LNCS 10939. Cham：Springer， 2018： 426-438.

[17] 朱庆峰，葛洪伟.K近邻相似度优化的密度峰聚类［J］.计算机工程与应用，2019，55（2）：148-153，252.（ZHU Q F， GE H W. Density peaks clustering optimized byKnearest neighbor’s similarity ［J］. Computer Engineering and Applications， 2019， 55（2）： 148-153， 252.）

[18] 邱保志，辛杭.一种基于共享近邻亲和度的聚类算法［J］.计算机工程与应用，2018，54（18）：184-187，222.（QIU B Z， XIN H. Shared nearest neighbor affinity based clustering algorithm ［J］. Computer Engineering and Applications， 2018， 54（18）： 184-187， 222.）

[19] 钱雪忠，金辉.自适应聚合策略优化的密度峰值聚类算法［J］.计算机科学与探索，2020，14（4）：712-720.（QIAN X Z， JIN H. Optimized density peak clustering algorithm by adaptive aggregation strategy ［J］. Journal of Frontiers of Computer Science and Technology ， 2020， 14（4）： 712-720.）

[20] LIU R， WANG H， YU X M. Shared-nearest-neighbor-based clustering by fast search and find of density peaks ［J］. Information Sciences， 2018， 450： 200-226.

[21] COVER T， HART P. Nearest neighbor pattern classification ［J］. IEEE Transactions on Information Theory，1967， 13（1）： 21-27.

[22] KORN F， MUTHUKRISHNAN S. Influence sets based on reverse nearest neighbor queries ［J］. ACM SIGMOD Record， 2000， 29（2）： 201-212.

[23] JARVIS R A， PATRICK E A. Clustering using a similarity measure based on shared near neighbors ［J］. IEEE Transactions on Computers， 1973， C-22（11）： 1025-1034.

[24] FREY B J， DUECK D. Clustering by passing messages between data points ［J］. Science， 2007， 315（5814）： 972-976.

[25] VINH N X， EPPS J， BAILEY J. Information theoretic measures for clusterings comparison： variants， properties， normalization and correction for chance ［J］. Journal of Machine Learning Research， 2010， 11： 2837-2854.

[26] FOWLKES E S， MALLOWS C L. A method for comparing two hierarchical clusterings ［J］. Journal of the American Statistical Association， 1983， 78（383）： 553-569.

Density peak clustering algorithm based on adaptive nearest neighbor parameters

ZHOU Huanhuan1， ZHENG Bochuan2*， ZHANG Zheng1， ZHANG Qi1

（1.School of Mathematics and Information，China West Normal University，Nanchong Sichuan637009，China；2.School of Computer Science，China West Normal University，Nanchong Sichuan637009，China）

Aiming at the problem that the nearest neighbor parameters need to be set manually in density peak clustering algorithm based on shared nearest neighbor， a density peak clustering algorithm based on adaptive nearest neighbor parameters was proposed. Firstly， the proposed nearest neighbor parameter search algorithm was used to automatically obtain the nearest neighbor parameters. Then， the clustering centers were selected through the decision diagram. Finally，according to the proposed allocation strategy of representative points， all sample points were clustered through allocating the representative points and the non-representative points sequentially. The clustering results of the proposed algorithm was compared with those of the six algorithms such as Shared-Nearest-Neighbor-based Clustering by fast search and find of Density Peaks （SNN‑DPC）， Clustering by fast search and find of Density Peaks （DPC）， Affinity Propagation （AP）， Ordering Points To Identify the Clustering Structure （OPTICS）， Density-Based Spatial Clustering of Applications with Noise （DBSCAN）， andK-means on the synthetic datasets and UCI datasets. Experimental results show that， the proposed algorithm is better than the other six algorithms on the evaluation indicators such as Adjusted Mutual Information （AMI）， Adjusted Rand Index （ARI） and Fowlkes and Mallows Index （FMI）. The proposed algorithm can automatically obtain the effective nearest neighbor parameters， and can better allocate the sample points in the edge region of the cluster.

shared nearest neighbor; local density; density peak clustering;k-neighbor; inverse neighbor

TP181

A

1001-9081（2022）05-1464-08

10.11772/j.issn.1001-9081.2021050753

2021⁃05⁃11；

2021⁃08⁃27；

2021⁃08⁃30。

国家自然科学基金资助项目（62176217）。

周欢欢（1996—），女，重庆人，硕士研究生，主要研究方向：机器学习、聚类分析； 郑伯川（1974—），男，四川自贡人，教授，博士，CCF会员，主要研究方向：机器学习、深度学习、计算机视觉； 张征（1978—），女，四川自贡人，副教授，硕士，主要研究方向：运筹与优化； 张琦（1996—），女，重庆人，硕士研究生，主要研究方向：机器学习、聚类分析。

This work is partially supported by National Natural Science Foundation of China （62176217）.

ZHOU Huanhuan， born in 1996， M. S. candidate. Her research interests include machine learning，clustering analysis.

ZHENG Bochuan， born in 1974， Ph. D.， professor. His research interests include machine learning， deep learning， computer vision.

ZHANG Zheng， born in 1978， M. S.， associate professor. Her research interests include operations research and optimization.

ZHANG Qi， born in 1996， M. S. candidate. Her research interests include machine learning， clustering analysis.