基于DEM仿真的种鹅精准饲喂装置设计优选研究*

聂传斌，孙卫明，张燕军，李佳眙，邢煜斌，龚道清

(1. 扬州大学机械工程学院，江苏扬州，225127； 2. 扬州大学动物科学与技术学院，江苏扬州，225009)

0 引言

我国是鹅的饲养与消费大国[1]，近年来鹅肉市场消费需求持续攀升，对养鹅产业链的源头—优质种鹅的质量提出了更高要求。传统养殖方式无法对家禽个体的生长特性以及采食规律进行精细化掌控，常常出现投喂过多或投喂过少造成的饲喂不均衡等问题，严重的甚至会引发家禽营养性疾病高发等问题[2]。为培育出优质鹅的品种和品系，现有育种技术普遍根据种鹅的生长速度和饲料转化率等[3]指标进行个体选育，但是采用较为粗放的人工投料饲喂方式，难以及时准确获得投料量、鹅只的采食量、鹅只体重等重要数据，进而直接影响优质种鹅的选育工作。

近年来，物联网、RFID、电子信息、人工智能等技术的快速发展，使得通过智能化的手段进行动物饲养、筛选和检测成为可能，如已有报道将物联网技术应用于种鸡、蛋鸡的生产管理中，实现对家禽质量进行追溯、将RFID及云计算技术应用于鸡育种、基于RFID与Zigbee的牛场远程监测等等。邱麦迪[4]设计了一种基于物联网的智能养殖管理设备，通过智能传感技术实现了实现羊只重量和羊饲料重量的动态测定。何俊等[5]设计了基于4G网络的妊娠母猪精准饲喂系统。

受限于鹅本身独特的活动习性和生理特点，目前缺乏有关种鹅的精准饲喂管理方法，如何对种鹅进行单元化管理，实时掌握个体生长发育情况，精准追踪种鹅在饲养过程中的饲料转化率情况是解决现有问题的关键环节。本文针对种鹅选育在饲喂方面存在的问题，设计了精准饲喂装置，通过RFID技术识别种鹅个体编号并同步感知个体的体重数据，根据采食位的种鹅个体信息从喂料口输出与之生长发育阶段对应的饲料量进行精准化饲喂。为实现定量投喂饲料，结合饲料的形态特点[6]设计微型螺旋输送机构，基于离散元方法对精准饲喂装置的饲料输送过程进行动态仿真分析，综合考虑饲料颗粒质量流率、出输送管道的速度以及螺旋叶片扭矩等因素，对微型精准饲喂螺旋输送机构的输送管道截面形状、螺旋叶片的类型和螺距等进行优选，为解决种鹅传统养殖方式中存在的人工投料饲喂方式粗犷、难以及时获得种鹅个体饲料转化率等难题提供技术支撑。

1 精准饲喂装置总体方案设计

1.1 精准饲喂装置结构设计

结合种鹅的采食特点设计精准饲喂装置，其整体结构如图1所示，主要包括饲料盛放筒、饲料输送机构、进食平台模块和控制器等，饲料存储模块由倒锥形的特制的无底饲料桶构成，饲料输送模块由搅拌下料棒、L形输送管道、螺旋叶片构成，步进电机在输送管道的一端与螺旋叶片相连，提供驱动力。在输送过程中饲料颗粒首先经饲料桶底部下落至输送管道入口所在平面，由搅拌下料棒将饲料均匀推送至每个输送管道入口，最后饲料受转动的螺旋叶片的作用被输送至饲料槽。进食平台模块由斜扇形进食平台、压力传感器、RFID线圈、饲料槽、料槽隔板构成，斜扇形进食平台符合种鹅侧身位伸长脖子进食的生活习性；压力传感器用于感知种鹅个体的体重；RFID线圈可读取种鹅脚踝处的RFID脚环编号数据识别个体身份；料槽隔板将环形料槽隔成多个独立的饲料槽单元。控制器模块通过识别种鹅个体身份、体重，结合生长发育曲线，驱动电机实现螺旋输送机构的定量出料。

图1 精准饲喂装置结构组成示意图

种鹅精准饲喂装置的优势体现在：(1)设计独立的进食平台，并为每只鹅分配单独的饲料槽段，确保种鹅在进食过程中不受其他个体的干扰，便于准确追踪种鹅个体的进食量和控制对其的饲料投喂量。(2)利用饲料颗粒和螺旋叶片之间的摩擦和推力进行饲料输送，建立步进电机转速、工作时间、功率和饲料质量流率之间的关系，达到精准输出、精细把控的目的。(3)通过压力传感器对种鹅个体准确称重，并建立种鹅生长周期的体重变化曲线，随时随地掌握饲喂过程中饲料转化率情况。(4)采用RFID射频阅读器在种鹅站上进食平台时读取种鹅RFID脚环电子标签，识别种鹅品种类型、所处生长周期等信息，建立可溯源的数据库，实现对种鹅的信息化管理和精准化饲喂。

1.2 精准饲喂装置控制方法

种鹅精准饲喂装置的控制方法和流程为：当种鹅站上站板时，站板下方的压力传感器采集鹅的体重数据，同时RFID射频阅读器读取鹅的RFID脚环，通过蓝牙传输将信息传输至计算机连接云平台。云平台根据不同品种的鹅在对应生长周期的理论投喂量，并根据其体重信息进行调控和修正，最终确定实际投喂量，计算出控制饲料输出的步进电机的当用功率，反馈至步进电机进行饲料输出。其中单次输出饲料的总时长为定值，通过改变步进电机的转速来智能化调节饲料投喂量，达到精准饲喂的目的。

螺旋输送机构的饲料输出量计算公式如式(1)所示。

(1)

式中：Q——输送量；

D——螺旋叶片直径；

n——螺旋轴转速；

t——螺距；

ρ——物料松散密度，即物料容重；

φ——物料填充系数，即物料输送过程中物料堆积截面积与螺旋输送机构截面积的比值；

C——倾斜系数。

2 精准饲喂装置优选方法

2.1 优选总体方案

精准饲喂的实现主要是根据螺旋输送机构运输颗粒及散体物料时运输量可控的原理，针对种鹅精准饲喂装置特点和实际饲喂量、精度需求，对微型螺旋输送机构的相关参数和结构形式进行优选。

微型螺旋输送机构的设计是精准饲喂装置功能实现的核心环节，本文以微型螺旋输送机构输送饲料时的输送效率、定量输送的精度把控以及速度的限制为优化方向，重点研究饲料输送的质量流率、螺旋叶片的扭矩和饲料颗粒的输出速度等指标，对螺旋输送机构的输送管道截面形状、螺旋叶片的类型和螺距进行优选。

2.2 优选方法

对精准饲喂装置中螺旋输送机构的设计分为三部分：首先是确定饲料颗粒的本征参数，选取合适的仿真模型；其次是设计螺旋输送机构关键参数和结构的组成方案，通过计算机对饲料输出效果进行仿真模拟；最后根据仿真结果和模拟数值制作样机，分析试验结果与仿真结果的误差。

精准饲喂装置中使用的螺旋输送机构为水平安装方式，而螺距、螺旋输送机构截面形状和螺旋轴类型为影响水平螺旋输送机构输送能力的主要因素，因此本研究以螺旋输送机构的截面形状、螺距和螺旋轴类型为变量，使用控制变量的方法交叉组合设计了6组仿真模拟方案，最终确定精准饲喂装置中使用的螺旋输送机构的结构类型与关键参数。

2.3 模型简化

仿真过程中被输送物质的物理性质和材料特性也是需要重点关注的因素[7]，参数设计不合理不仅会影响传输精度和效率，造成耗能增加，而且会导致物料破损[8]。传统养殖使用的饲料是养殖户使用麦麸、豆粕、玉米、米糠等原料兑水搅拌后形成的糊状物，这种人工配比的传统饲料存在营养性不均衡的缺陷。精准装置使用的饲料是经原材料加工完成后的固体颗粒饲料，在进行数值模拟仿真时可以不考虑饲料颗粒之间的粘滞性作用；又因为装置中采用的螺旋输送机构为短距离传输，输送管道内气流对饲料颗粒的影响可以忽略不计，因此本研究建立的模型是单相固体颗粒离散元仿真模型。

3 仿真参数标定

离散元法(Discrete Element Method, DEM)是把研究对象分离为刚性元素的集合，以牛顿第二定律作为理论基础，解决不连续介质问题的数值模拟方法[9]，利用EDEM软件对螺旋输送机构进行数值仿真设计，具有成本低、周期短、精度高等优势。在使用EDEM软件进行仿真时，Michele等[10]认为关键在于对仿真模型的微观参数进行标定，包括接触参数和本征参数，微观参数的精度决定了仿真结果是否能够与现实情况相吻合。其中接触参数包括颗粒与颗粒之间、颗粒与环境材料之间的碰撞恢复系数、静摩擦系数以及滚动摩擦系数[11]，本征参数包括宏观物性参数和微观物性参数，微观物性参数包括颗粒和环境材料的密度、泊松比以及弹性模量，宏观物性参数包括颗粒的尺寸、形状等[12]。

为提高仿真结果的可靠性，本研究使用模拟仿真与试验相结合的方法，对上述涉及参数进行标定和校准。分别采用堆积角实验[13]、碰撞弹跳实验、斜面滑移实验、斜面滚动实验[14]来标定和校准颗粒与颗粒之间的接触参数、颗粒与螺旋输送机构材料之间的碰撞恢复系数、静摩擦系数、滚动摩擦系数。

3.1 本征参数确定

1) 饲料容重。饲料颗粒在堆积时颗粒之间会形成不均匀间隙，因此密度(单位体积饲料的质量)不再能够表示饲料整体的物理特性。饲料颗粒在不受外部挤压力的情况下自然堆积，当堆积体积相等时，其总质量也是相等的，这就是饲料的容重。本文通过精密天平和定体积容器测量和计算得到饲料颗粒的容重为584.43kg/m3。

2) 饲料颗粒的筛选和分类。饲料颗粒在储存、运输过程中受外界挤压、碰撞以及颗粒之间的作用力时，会导致饲料颗粒破碎并产生大小不均匀的颗粒和粉末。一般可采用先人工筛分后称重的方法来测定饲料的含粉率[15]，本研究采用的饲料形状近似为圆柱体，故以饲料颗粒的轴径比γ为分类标准，选取一定量的饲料样本将饲料分为大、中、小颗粒以及粉末四种，最终计算获得各成分的含量，分类标准和各组分含量见表1。

表1 饲料颗粒的分类及含量Tab. 1 Classification and content of feed granules

3) 饲料的弹性模量和泊松比。González-Montellano等[16]通过研究发现，当颗粒在没有严重受到压缩时对其进行仿真试验，杨氏模量与泊松比的参数取值对仿真结果的影响不大。本文确定的饲料的泊松比为0.4，杨氏模量为273.9 MPa[13]。

4) 螺旋输送机构材质。制作精准饲喂装置样机时，螺旋输送机构选用表面质量高、韧性表现优异、适合结构验证的ASTMD 638新型树脂材料，其物性参数见表2。

表2 ASTMD 638材料参数表Tab. 2 Material parameter table of ASTMD 638

3.2 颗粒模型建立

本文在建立颗粒模型时，首先将饲料颗粒人工筛选并分成大颗粒饲料、中等颗粒饲料、小颗粒饲料和饲料粉末4种(图2)，然后建立颗粒模板并划分网格，在EDEM中使用自动填充生成颗粒模型。其中大饲料颗粒为长9.8 mm，截面直径3.5 mm的圆柱体；中等饲料颗粒为长5.3 mm，截面直径3.5 mm的圆柱体；小饲料颗粒为长2.8 mm，截面直径3.5 mm的圆柱体；饲料粉末为直径小于0.25 mm的圆球，且上述四种大小颗粒的体积均服从正态分布。

(a) 大颗粒

(c) 小颗粒

(d) 粉末

图2 饲料颗粒模型

Fig. 2 Model diagram of feed particles

3.3 接触模型确定

在颗粒接触力学[17]中，常见的颗粒接触理论有Hertz接触理论、JKR接触理论和DMT接触理论等。其中Hertz接触理论[18]是颗粒曲面弹性接触问题的理论基础，适用于球体、柱体等形状颗粒的弹性接触。JKR接触理论[19]在Hertz接触理论的基础上考虑了颗粒接触表面分子或原子间的黏连作用，适用于大粒径、低黏附能的低弹性模量材料。DMT接触理论考虑了颗粒接触面间的范德华力，适用于小粒径、高黏附能的高弹性模量材料。

本文采用的饲料颗粒为相对干燥的柱状颗粒，颗粒之间不存在受水分作用产生的液桥力和受范德华力作用发生的黏附现象，因此综合考虑选择经典的Hertz-Mindlin接触模型作为研究过程中饲料颗粒的接触模型。

3.4 饲料颗粒间接触参数确定

堆积角(图3)是颗粒材料属性和接触属性的宏观表现形式，常用来判定离散元仿真中参数设置的合理性。本文通过建立饲料颗粒堆积的数值计算模型，利用EDEM软件仿真模拟，逆向标定和校准计算模型中颗粒与颗粒间接触参数的设定值。

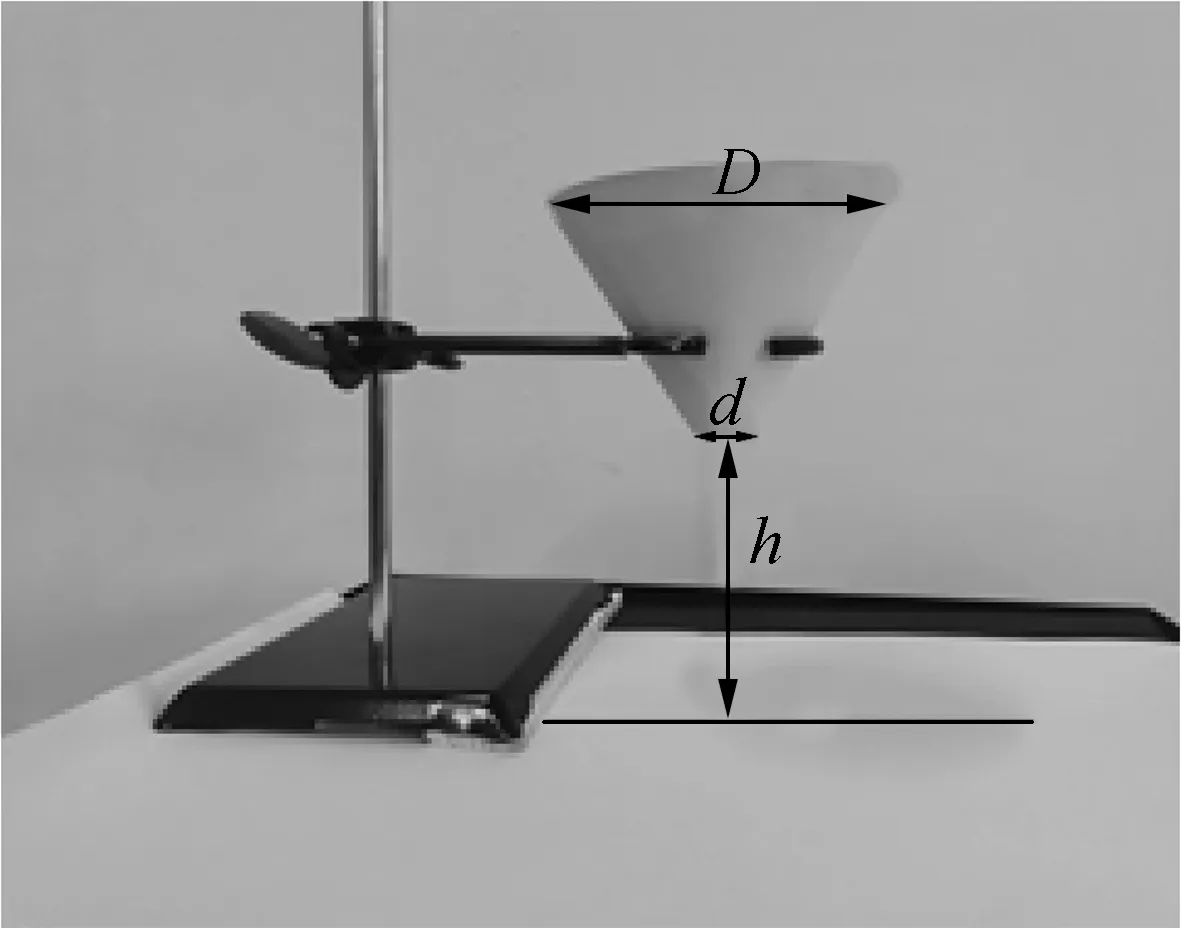
图3 堆积角试验装置图

试验装置由堆积平面、台架装置和漏斗装置构成，使用台架将预置有饲料颗粒的漏斗容器提升后使饲料颗粒自由落下，待饲料堆稳定后测定饲料堆颗粒的堆积角。为减小试验误差，重复试验并从前视、后视、左视和右视方向水平拍摄饲料堆的堆积角(图4)，利用Matlab软件先对所拍摄的照片进行二值化图像处理，再使用GetData软件在二值化后的图像轮廓的一侧边缘上取点后使用直线拟合，该直线与水平方向的夹角即为堆积角，计算其平均值，得到饲料颗粒的堆积角的试验值为28.15°。

图4 堆积角α示意图

使用Solid works建立堆积角试验装置的简易三维几何模型，导入EDEM进行仿真(图5)。在预试验的基础上，设置不同组合的饲料颗粒与颗粒之间的静摩擦系数、碰撞恢复系数和滚动摩擦系数，分别进行仿真模拟，并将仿真结果与试验结果相比，选取最优组合。当饲料颗粒与颗粒之间的静摩擦系数、碰撞恢复系数和滚动摩擦系数分别为0.4、0.2和0.01时，仿真模拟得到的堆积角为29.74°，与试验值相比较存在的误差仅为5.6%，表明仿真结果比较精确，选取该组参数为最终标定结果。

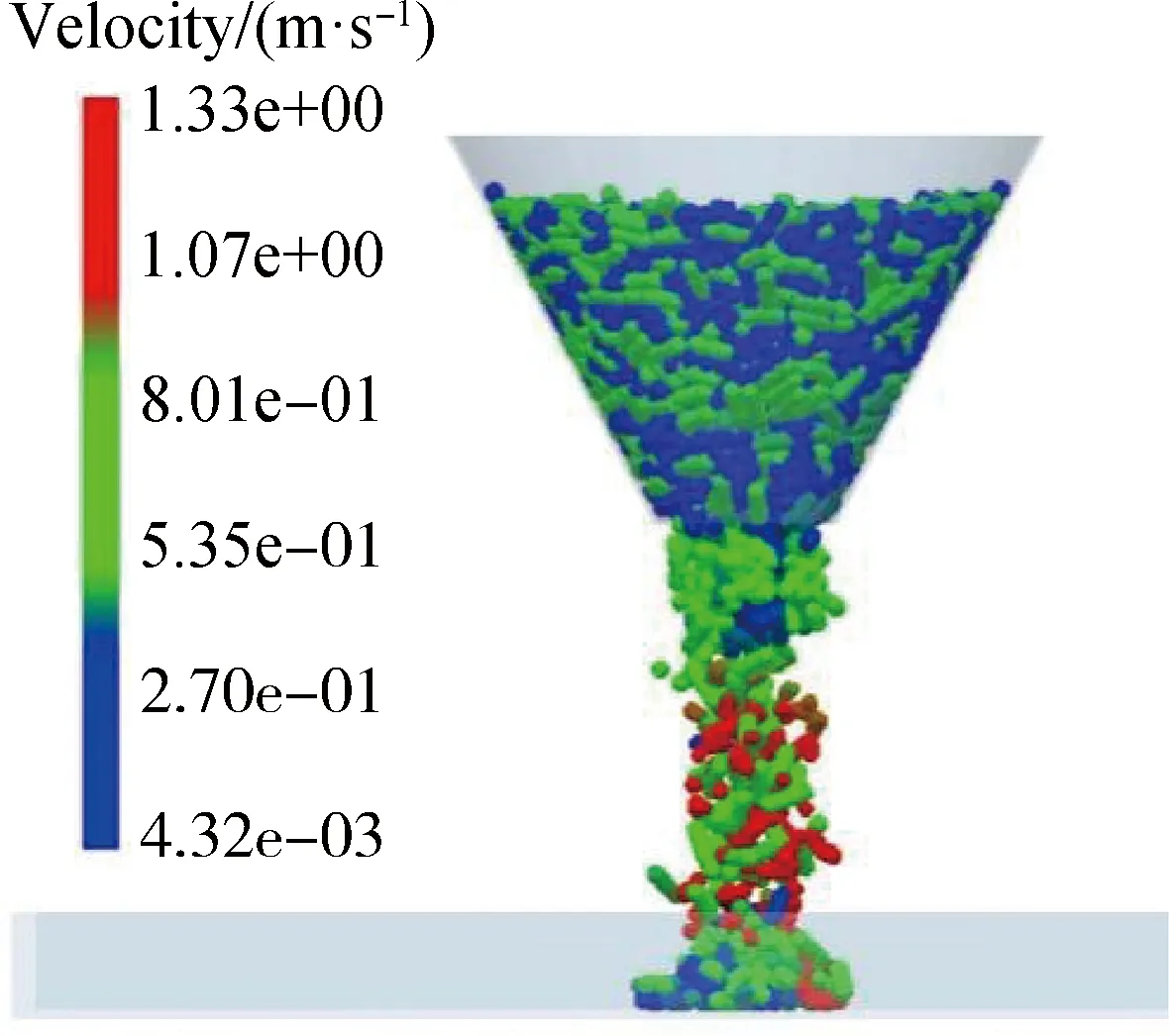
图5 仿真过程示意图

3.5 饲料与环境间接触参数确定

1) 静摩擦系数确定。本文根据斜面法的试验原理，设计了简易的斜面仪器，通过平面滑移试验测定饲料颗粒与螺旋输送机构所用材料之间的静摩擦系数。在试验中为防止饲料颗粒滚动，降低测量结果的误差，将3颗饲料颗粒粘连在一起，初始时刻将其放于水平的树脂材料斜面上，缓慢增大斜面倾角，当饲料颗粒开始滑移时停止增大，用电子量角器测量并记录此时斜面倾斜角度。重复试验并计算其平均值，得到使饲料颗粒开始滑移的斜面倾斜角度的试验值θ1=28.64°。

根据物料静摩擦因素与静摩擦角的数值关系式μ=tanθ1，得到饲料颗粒与螺旋输送机构材料之间的静摩擦系数μ=0.546。

2) 滚动摩擦系数的确定。根据能量守恒原理，颗粒在固定的高度从固定倾角的斜面滚下时，在水平面上的滚动位移取决于颗粒与平面之间的滚动摩擦系数，本文采用斜面滚动试验来标定饲料颗粒与树脂材料之间的滚动摩擦系数。

将饲料颗粒放置于倾斜角α=30°的树脂材料斜面上，使其从垂直高度h=150 mm的位置以零初速度沿斜面向下滚动，饲料颗粒最终静止在树脂材料水平面上。测量饲料颗粒的水平滚动距离，重复试验计算其平均值，得到饲料颗粒的水平滚动距离的试验值s=208.43 mm。

建立斜面滚动试验的等效模型，使用EDEM进行模拟仿真标定滚动摩擦系数。由于在进行该试验时是测量单颗饲料颗粒的水平滚动距离，所以饲料颗粒与颗粒之间的碰撞恢复系数、静摩擦系数和滚动摩擦系数对试验结果无影响；又因为饲料颗粒是静止无初速度放置在斜面上且只有无滑动的纯滚动运动，故饲料颗粒与斜面之间的碰撞恢复系数和静摩擦系数对试验结果也没有影响。为了避免干扰，在EDEM仿真试验中，将上述参数均设置为0。

经过预仿真试验，饲料颗粒与树脂材料之间的滚动摩擦系数λ的范围是0.01～0.06，以0.01为步长，进行6组仿真试验，每组进行5次试验并取平均值，试验设计方法与结果如表3所示。

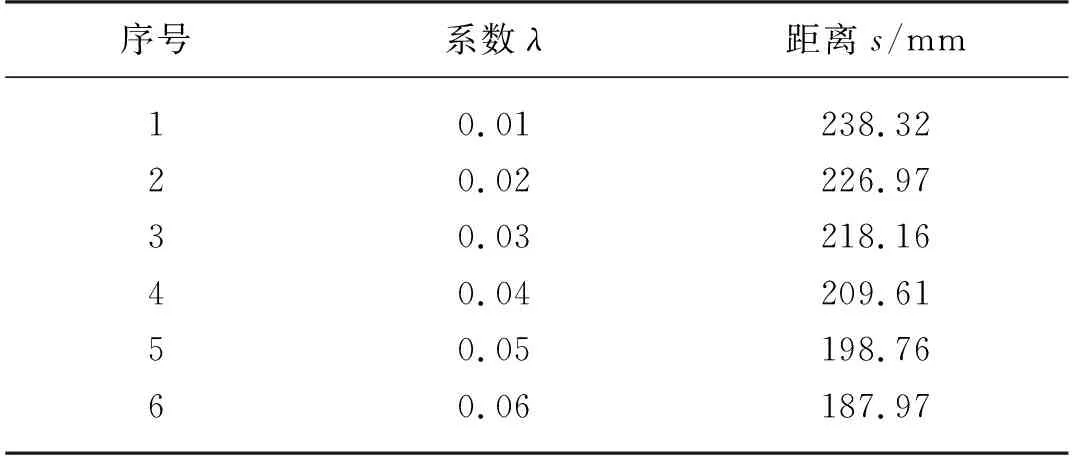
表3 滚动摩擦系数试验设计与结果Tab. 3 Experimental design and results of rolling friction coefficient

拟合上述数据得到水平滚动距离s和滚动摩擦系数λ之间的关系式如式(2)所示。

s=-957.1λ2-918.5λ+246.9

(2)

经计算得到该拟合的误差平方和为R2=0.998 2，接近于1，表明拟合优度较高。取水平滚动距离s为208.43 mm，得到饲料颗粒与树脂材料之间的滚动摩擦系数为λ=0.040 2。

3) 碰撞恢复系数的确定。碰撞恢复系数是反映物体碰撞损失的重要参数[20]，已知碰撞恢复系数的计算公式如式(3)所示。

(3)

式中：v2——发生碰撞时树脂材料的速度；

v20——碰撞后树脂材料的速度；

v1——发生碰撞时饲料颗粒的速度；

v10——碰撞后饲料颗粒的速度；

v2-v1——发生碰撞后两物体的分离速度；

v10-v20——发生碰撞前两物体的接近速度。

(4)

设计碰撞弹跳试验来测量计算饲料颗粒与树脂材料之间的碰撞恢复系数。将饲料颗粒用镊子提升到距树脂材料平面高度为15 cm处，静止无初速度释放后，使用工业高速相机系统对下落过程和反弹过程进行拍摄，并将饲料反弹至最高点的单帧画面导出，根据比例尺测量计算并记录数值。重复试验，取平均值，得到饲料颗粒碰撞后的最大反弹高度为23.4 mm，计算出碰撞恢复系数e=0.394。

4 饲料输送过程仿真与分析

由于精准化饲喂的实现主要依靠螺旋输送机构输送物料时输送量可控的特点，因此对种鹅精准饲喂装置饲料输出模块中采用的螺旋输送机构进行参数设计和结构优选至关重要。

4.1 仿真试验组设计

根据精准饲喂装置实际尺寸设计要求确定螺旋输送机构输送管道和螺旋叶片的基本尺寸，分别控制输送管道截面形状、螺旋叶片类型、螺旋叶片螺距为单一变量，设计仿真试验组(表4)。

建立螺旋输送机构三维模型，根据上文中相关参数的标定和测量结果在EDEM中设置仿真参数进行仿真计算，通过饲料颗粒的质量流速率、输出速度和螺旋叶片的扭矩来分析不同结构特点的螺旋输送机构的传输效果。

图6所示为不同截面形状和螺旋叶片螺距的螺旋输送机构仿真过程示意图，图中箭头方向表示饲料颗粒在输送过程中的流向，箭头的颜色表示饲料颗粒的速度大小。

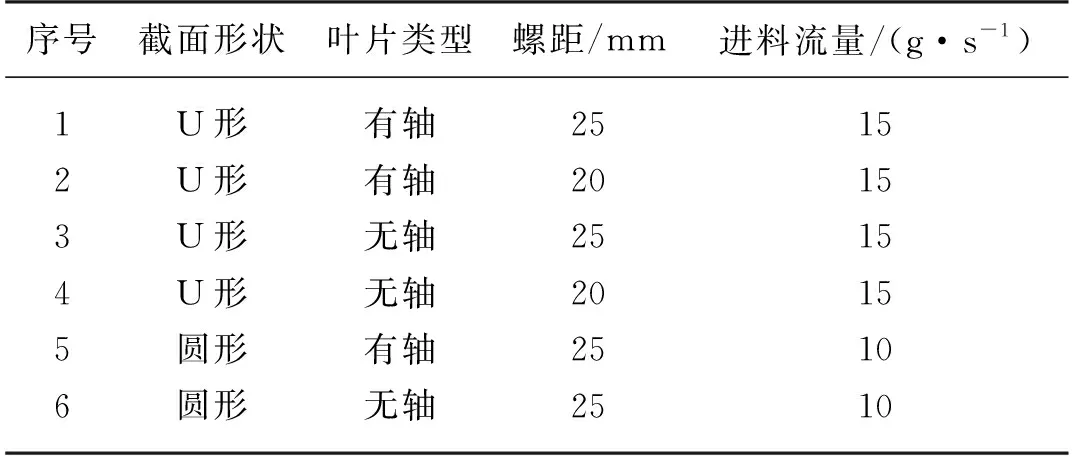
表4 试验组设计Tab. 4 Design of experimental group

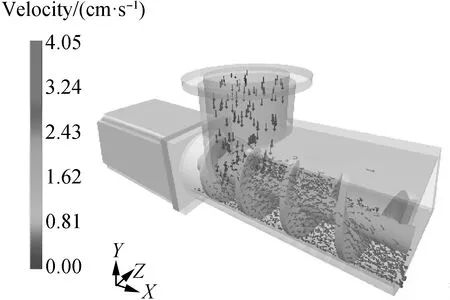
图6 仿真过程示意图

4.2 质量流率分析

4.2.1 以截面形状为变量

以输送管道的截面形状为研究变量，选取有螺旋轴且螺距为25 mm的螺旋叶片为例，通过仿真试验得到输送管道截面形状为圆形的螺旋输送机构在输送饲料过程中的平均质量流率为10.47 g/s，而输送管道截面形状为U形的螺旋输送机构在输送饲料过程中的平均质量流率为7.32 g/s。质量流率随仿真时间变化的曲线如图7所示，从图中可知在输料过程中，输送管道截面形状为圆形时的饲料输出质量流率明显大于输送管道截面形状为U形的螺旋输送机构。

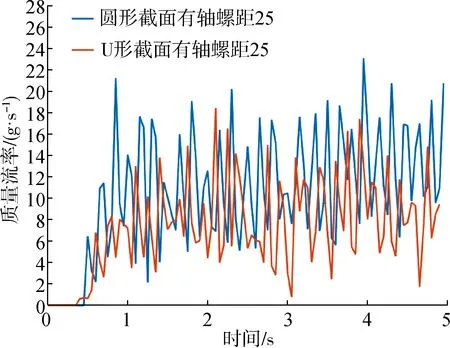
图7 不同截面形状下的质量流率

4.2.2 以螺旋叶片类型为变量

以螺旋叶片的类型为研究变量，选取圆形截面输送管道，对于螺旋叶片螺距为25 mm的螺旋输送机构，通过仿真试验得到螺旋叶片类型为有轴的圆形截面螺旋输送机构在输送饲料过程中的平均质量流率为10.47 g/s，而螺旋叶片类型为无轴的圆形截面螺旋输送机构在输送饲料过程中的平均质量流率为7.35 g/s。质量流率随仿真时间变化的曲线如图8所示，从图8中可知螺旋叶片含有螺旋轴的螺旋输送机构在输送饲料过程中的质量流率要明显大于螺旋叶片不含螺旋轴的螺旋输送机构。产生这一现象的原因是位于无轴螺旋叶片空腔位置的较小饲料颗粒在输送过程中得不到有效的、持续的推力作用，且由于饲料颗粒之间存在的运动阻力，导致部分饲料在输送管道内滞留的时间过长；而有轴的螺旋叶片不仅能够持续提供推力，还能有效减少输送管道内饲料颗粒的接触和互相阻碍作用。

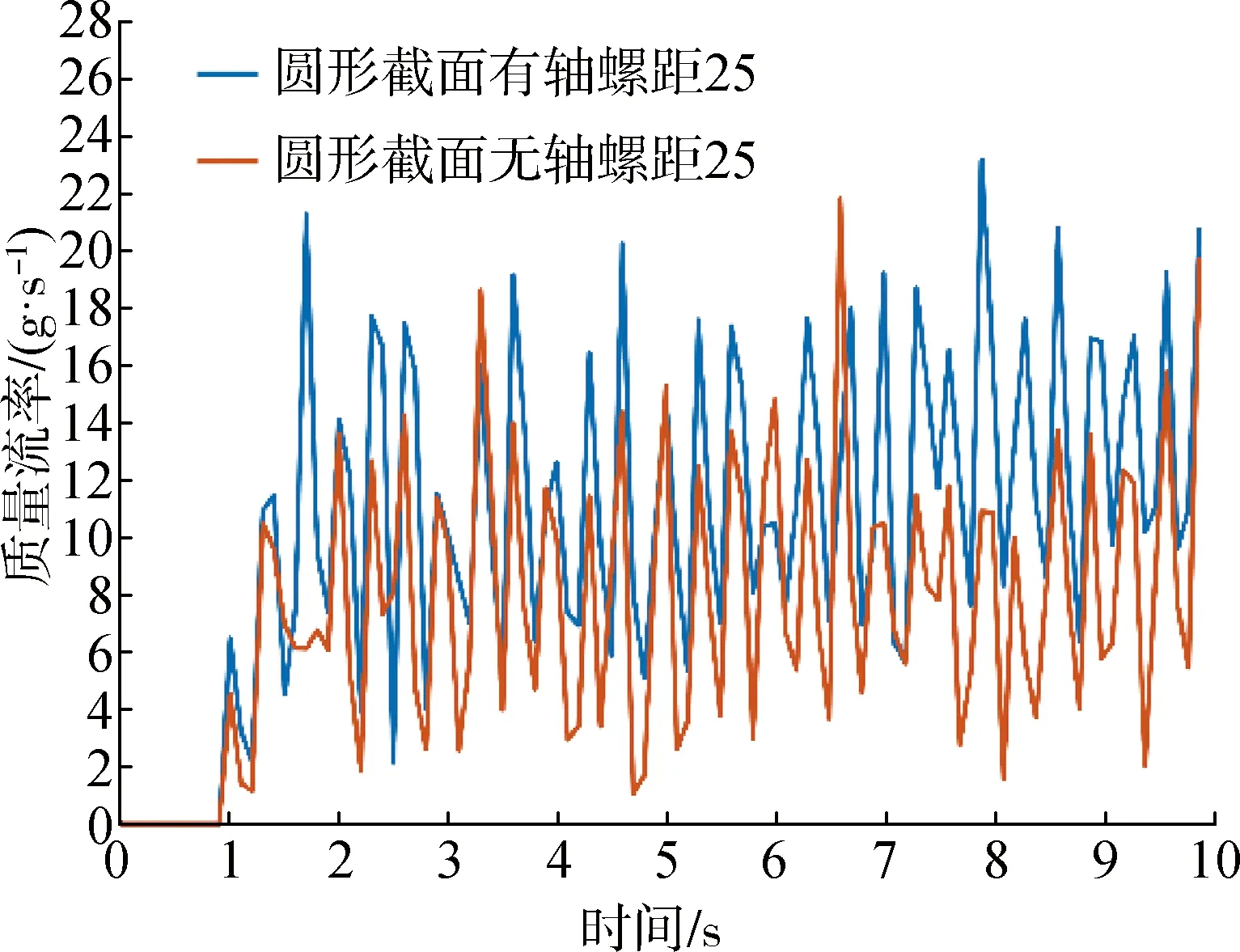
图8 不同螺旋叶片类型下的质量流率

4.2.3 以螺旋叶片螺距为变量

以螺旋叶片螺距为研究变量，选取U形截面输送管道、螺旋叶片类型为有轴的螺旋输送机构为例，通过仿真试验得到螺旋轴螺距为20 mm的输送机构饲料输出质量流率的方差为20.67，而螺旋轴螺距为25 mm的输送机构饲料输出质量流率的方差为15.74。输送过程中不同时刻的质量流率的分布如图9和图10所示。

图9 螺距为20 mm时的质量流率分布

图10 螺距为25 mm时的质量流率分布

从图9和图10可知采用截面形状为U形、螺旋轴类型为有轴的螺旋输送机构，在输送饲料过程中，螺旋轴螺距为25 mm时饲料输出的质量流率更加符合正态分布，这说明在控制其他变量相同情况下，螺旋轴螺距为25 mm的输送机构输出饲料时质量流率更稳定，随时间的脉动性更小。

4.3 颗粒速度分析

饲料颗粒经螺旋输送机构输送到输送管道出口后，可视为做以输出口颗粒速度为初速度的平抛运动，为避免饲料颗粒落入饲料槽外，需要限制颗粒输出速度，并根据颗粒速度设计合适的螺旋叶片转速。根据种鹅精准饲喂装置实际结构设计，螺旋输送机构出口位于饲料槽上方5 cm处，且距离饲料槽最外侧边缘20 cm，使用平抛运动位移计算公式(5)，计算得出饲料颗粒从输送管道飞出的速度要小于0.25 m/s。

(5)

图11所示为颗粒速度仿真分析结果，从图11中可知当设置螺旋叶片的转速为18.85 rad/s时，6个试验组对应的饲料颗粒飞出速度能够满足上述条件，其中约90%的饲料颗粒飞出速度均集中0.15～0.2 m/s。

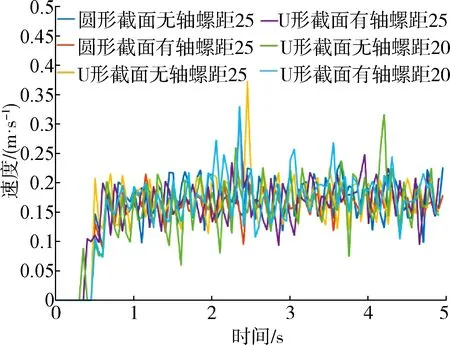
图11 颗粒速度分析图

4.4 螺旋叶片扭矩分析

在螺旋叶片的转速相同情况下，螺旋输送机构输送饲料颗粒所需的功率取决于螺旋叶片的扭矩，如式(6)所示。

P=T×ω

(6)

式中：P——功率；

T——螺旋叶片扭矩；

ω——螺旋叶片角速度。

螺旋叶片的在输送过程中的扭矩越大，步进电机需要提供的功率越大。分别以输送管道的截面形状、螺旋叶片的螺距和螺旋叶片的类型为研究变量，分析得到饲料颗粒输送过程中扭矩与上述变量的关系图(图12～图14)。

图12 不同截面形状下的扭矩分析

(a) U形截面

图14 不同螺距下的扭矩分析

由图12可知，圆形截面输送管道的螺旋输送机构在输送过程中，螺旋叶片的扭矩明显大于U形截面输送管道的螺旋输送机构，其中圆形截面输送管道在输送过程中的螺旋叶片平均扭矩为29.30 N·m，而U形截面输送管道在输送过程中的螺旋叶片平均扭矩为19.71 N·m。主要原因是U形输送管道的容量更大，在输送等量的饲料时，饲料颗粒的填充率(图13)要小于圆形输送管道。填充率大导致饲料颗粒之间、饲料颗粒与管道和螺旋叶片之间的碰撞挤压频率增加，因此需要更大的扭矩来维持螺旋叶片的转速。

由图14可知，螺距为25 mm的螺旋叶片在输料过程中所需的扭矩为19.71 N·m，而螺距为20 mm的螺旋叶片在输料过程中所需的扭矩为40.86 N·m。因为螺距越小，螺旋叶片的圈数越密集，其占据的空间越大，在输送管道长度和截面尺寸一定的情况下，留给饲料颗粒的空间越小(图15)，导致大量的饲料颗粒在有限的空间内受到碰撞和挤压作用，因此需要更大的扭矩来驱动螺旋叶片转动。

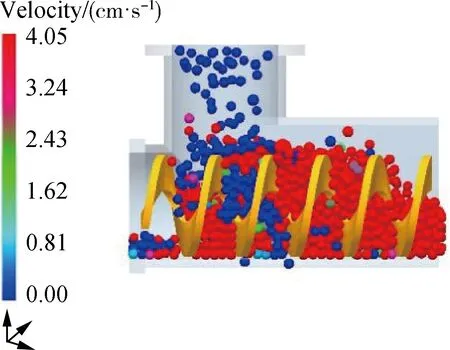
(a) 螺距20 mm

(b) 螺距25 mm

由图16可知，在其他变量相同的情况下，无轴螺旋叶片和有轴螺旋叶片在输料过程中所需的扭矩基本相同，分别为19.71 N·m和19.04 N·m，而包含螺旋轴的螺旋输送机构的结构强度更高。对于无轴螺旋叶片，因为它具有较强的抗缠绕和防堵料特性，常用于有轴螺旋输送机构不能或不宜输送的粘附性较强的物料、糊状粘稠物料以及易缠绕物料的输送工况[21]。

4.5 饲喂装置螺旋输送机构定型

种鹅精准饲喂装置精准投料功能的实现主要依靠螺旋输送机构在输送颗粒物料时运输量可控的特点，由上文仿真分析已知：输送管道截面形状为U形、螺旋叶片螺距为25 mm、螺旋叶片类型为有螺旋轴的螺旋输送机构相比于其他结构和型号的螺旋输送机构具有以下优点：(1)饲料颗粒质量流率分布符合正态分布，且质量流率更小，更有利于精准投料的把控。(2)输送同等质量的饲料时螺旋叶片所需的扭矩更小，在相同螺旋叶片转速下，步进电机的消耗功率更小，有利于减少能耗。(3)在输送过程中饲料颗粒的填充率更小，能够有效降低饲料颗粒之间、饲料颗粒与输送管道、螺旋叶片之间的碰撞频率和挤压程度，有利于减少饲料颗粒在输送过程中的破碎情况和提高装置的使用寿命。

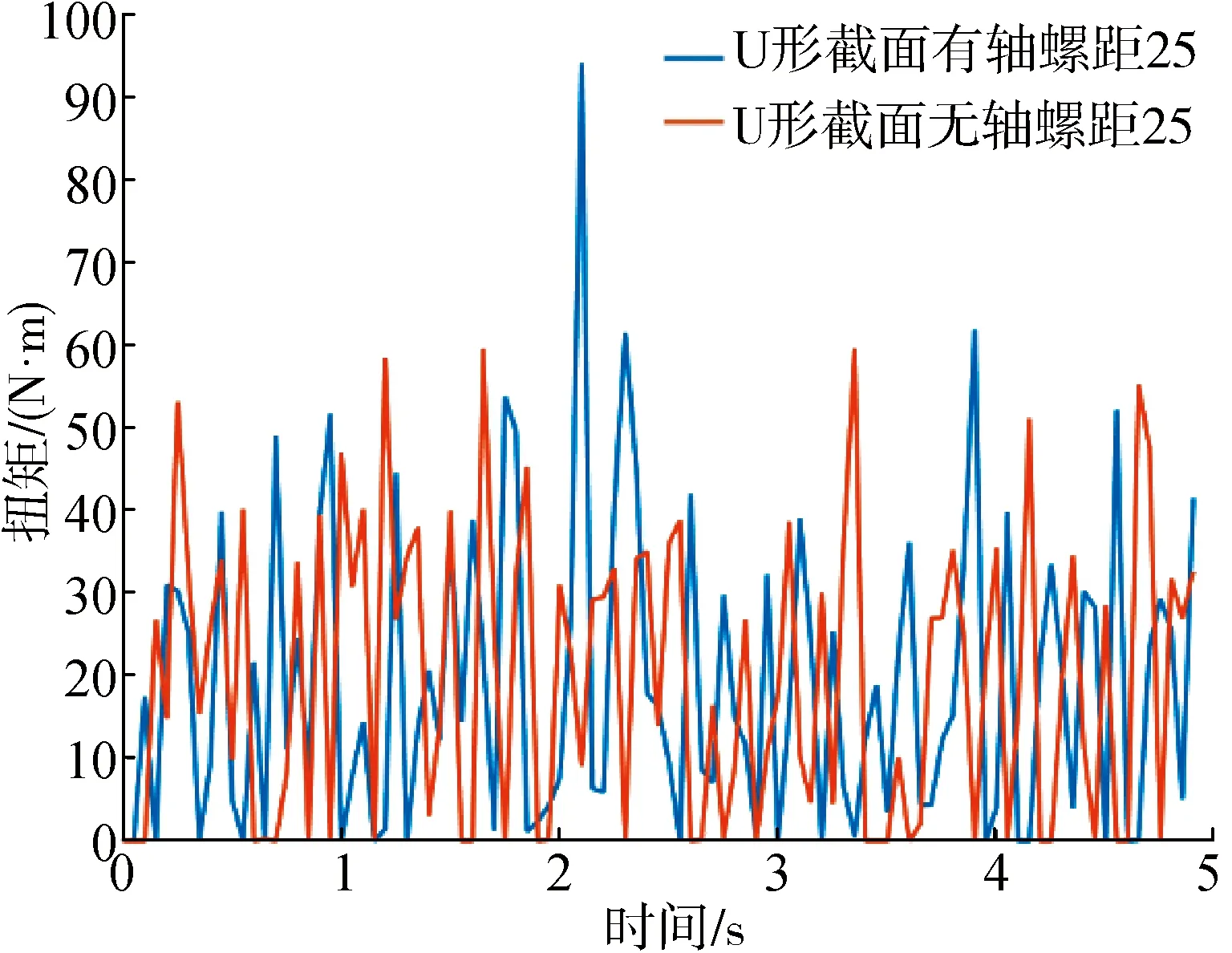
图16 不同螺旋叶片类型下的扭矩分析

5 结论

针对目前国内外种鹅优质品种品系选育产业存在的问题设计了种鹅精准饲喂装置，在解决饲喂不均衡和饲料浪费等问题的同时，为种鹅饲喂过程中饲料转化率的精细化研究提供了可能性。

基于DEM仿真技术对精准饲喂装置饲料输送过程进行仿真分析，综合饲料颗粒质量流率、飞出输送管道的速度以及螺旋叶片扭矩等因素，对螺旋输送机构的输送管道截面形状、螺旋叶片的类型和螺距进行设计和选型，达到降低能耗、提高输送效率、减少饲料破损率、增加装置使用寿命的目的。研究结果表明：在精准饲喂装置中，针对柱状种鹅饲料(大饲料颗粒为长9.8 mm，截面直径3.5 mm的圆柱体；中等饲料颗粒为长5.3 mm，截面直径3.5 mm的圆柱体；小饲料颗粒为长2.8 mm，截面直径3.5 mm的圆柱体；饲料粉末为直径小于0.25 mm的圆球，且上述四种大小颗粒的体积均服从正态分布)，采用输送管道截面形状为U形、螺旋叶片螺距为25 mm、螺旋叶片类型为有螺旋轴的螺旋输送机构时，饲料颗粒输出的平均质量流率为7.32 g/s，螺旋叶片收到的平均扭矩为19.04 N·m，约90%的饲料颗粒飞出速度均集中0.15～0.2 m/s，相比于其他结构形式的输送机构具有输送精度高、饲料破损率低、输送扭矩小等优势。