具有目标导向性的RRT路径规划研究

郭孝坤 吴玉秀 李景 程瑞嘉

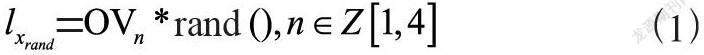
摘  要：在机器人全局路径规划中，首先对全局路径规划的各种探索路径的算法做了总结，对RRT、A*和D*算法做了对比，分析了这些算法的优缺点。鉴于RRT具有概率完备性，A*和D*具有深度优先性，也就是目标导向性，文章使用一种算法更改了原RRT算法中随机点的选取方式，使RRT具有概率完备性的同时也拥有了目标导向性，实验证明，改进后的RRT算法能够更快探索出到达目标点的路径。

关键词：全局路径规划;RRT;A*;深度优先性;概率完备性

中国分类号：TP242           文献标识码：A文章编号：2096-4706（2022）01-0069-05

Abstract： In the global path planning of robots， we first summarize the various path exploration algorithms of the global path planning， compare the RRT， A* and D* algorithms， and analyze their advantages and disadvantages. Given that RRT has probability completeness， A* and D* has depth priority， that is target orientation， this paper uses an algorithm to change the selection method of random points in the original RRT algorithm and make RRT have probability completeness and target orientation at the same time. The experiment proves that improved RRT algorithm can faster explore the path to reach the target point.

Keywords： global path planning; RRT; A*; depth priority; probability completeness

0  引  言

机器人应用中，路径规划是必须且首先需要的核心技术[1]，很多后续任务也都是从路径规划开始。目前路径规划可分为局部路径规划和全局路径规划，本文主要研究了全局路径规划下的路径探索问题。全局路径规划意思是机器人已知全局环境信息，通过拓扑法、可视图法、栅格法将全局信息转化为机器人易处理的信息，并在此基础上做路径探索。常见的路径探索方法主要有A*、D*、RRT法等。

A*算法在保证避障的前提下总是期望下一步尽可能接近目标点[2]，这种路径规划方式有着深度优先的特点，他能快速接近目标点。但是缺点也很明显，它容易陷入局部最优，如遇上凹型障碍物规划的路径容易一直转圈。D*算法[3]类似A*，不同的是D*算法从目标点开始向起始点搜索，在动态环境中有不俗的表现，他可以在环境发生变化时不断遍历节点从而找出新的最短路径，但是这种算法是以牺牲效率为代价的。RRT算法的核心思路是以起始点开始不断在地图上扩展探寻，直至找到目标点为止，其作出的探索路径像是一颗不断生长的树[4]。RRT是一种具有概率完备性的路径探索算法，也就是RRT算法理论上一定可以找到通往目标点的路径，并且依靠随机性，RRT算法搜索目标点的速度要远远高于完整搜索算法，且不会陷入局部最优。RRT算法缺点是搜索全局路径效率没有A*和D*高，并且搜索出来的路径也不是最优最短。

本文基于上述全局路径规划方法，分析了各种路径规划算法的优缺点，最终研究并改进了RRT算法，使得RRT算法在拥有概率完备性的同时又能拥有A*和D*深度优先的优点。

1  传统RRT算法概述

RRT全称快速扩展随机树，其算法的核心理论是以机器人初始起点作为树的根节点，在向着地图的任意方向随机采样，以采样点连接树中已存在且最靠近的节点向着采样点延伸新节点的方式生长树的新节点，当树的新节点成功探寻到目标点的时候停止。从该新节点开始找他的父节点，直到找到根节点。这样就找到一条通往目标点的可行路径[5]。

1.1  传统RRT算法步骤

对地图进行SLAM建模，不考虑智能体所处环境出现上坡下坡等特殊环境，假定处于二维平面工作空间W（WorkSapce）中，W∈R2。对传统RRT路径算法步骤描述如下：将智能体的起点xinit作为随机树的根节点;在Wfree中随机选择一个坐标记做xrand;使用Nearest_Neihbor（）函数寻找随机树上所有节点，距离xrand最近的节点向着xrand的方向生长出新的节点，记做xnear;反复调用EXTEND（）函数使xnear尽可能接近xrand，直到xnear完成到达xrand点、靠近障碍物、到达限制长度和接近目标点四个目标中的一个为止，将这个xnear添加到随机树中，此时随机树成功产生一个新的节点xnew。重复选取xrand，重复添加新的xnear，直到上述算法成功找到使xnew到达目标點区域范围内，程序结束，具体算法描述为：

Function：RRT（n∈Wfree，Δt∈R）

1：T.init（xinit）

2：for a=0; a<n;a++

3：xran←RANDOM_NODE（Wfree）

4：EXTEND（T， xrand）

5：end for

6：return T

Function：EXTEND（T， xrand）

1：xnear←Nearet_Neighbor （T， xrand）

2：u←Select_Input （xrand， xnew）

3：xnew←New_State（xnear， u， Δt）

4：if NoCollision Path（xnear， xnew） then

5：T. Add_Node（xnew）

6：T.Add_Edge（xnear， xnew， u）

7：end if

8：return T

1.2  传统RRT算法图解

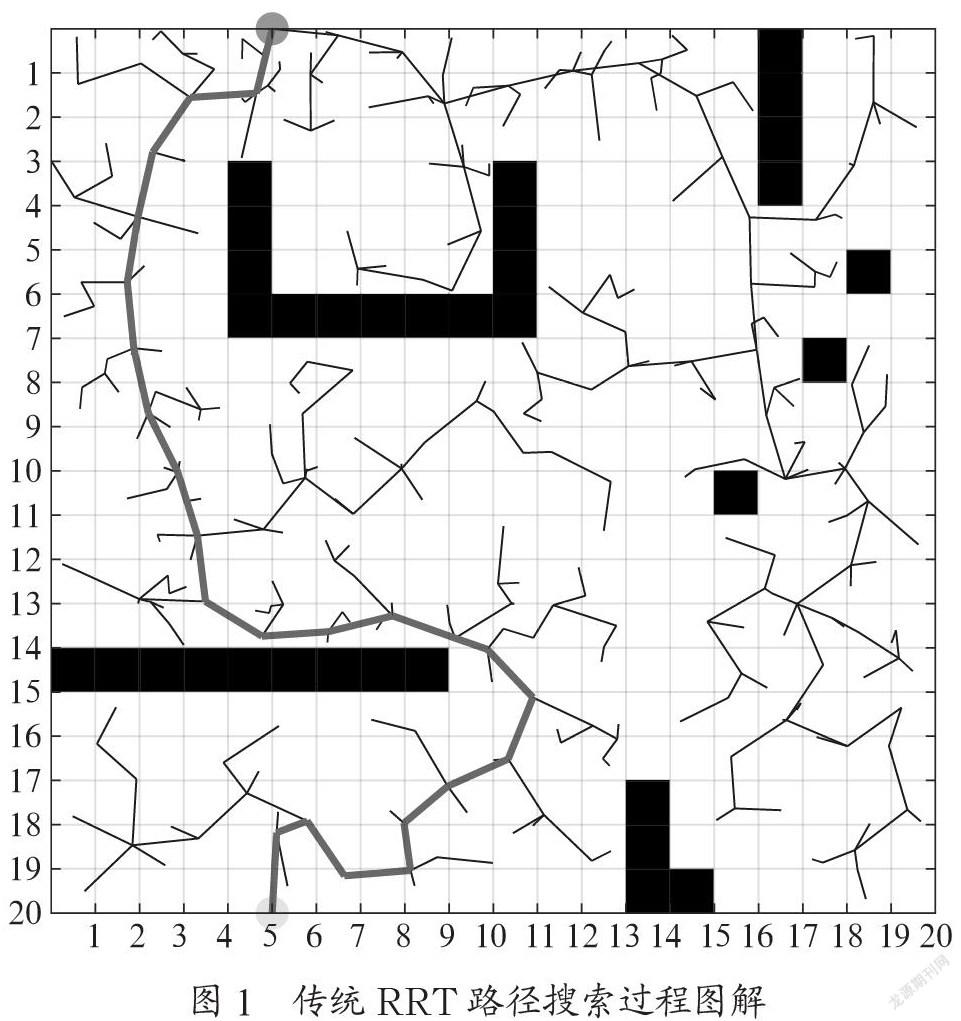
RRT大致过程如图1所示，图中绿色光点代表起始点，黄色光点代表终点，经过一段时间的搜寻，RRT算法最终找到了目标点，图中粉红色线段代表RRT算法找出的路径。可以看出传统RRT路径在地图的每一个角落都进行了搜索，他探索的路径不一定是最优的，但一定可以找到目标点。

2  改进的RRT算法

2.1  改进的RRT算法介绍

通过图1可以看出传统RRT算法虽然通过概率完备性成功在地图上找到了通往目标点的路径，但是RRT做了很多无用功，有些不必要搜索的地方RRT也做了探寻。如果给RRT算法提供一个朝向目标的大体方向，使RRT向着目标点的方向探寻，那么探寻目标点的效率就会提高很多。因此本文对传统RRT算法做了改进，使之添加了一种目标导向性的特性。

根據上述算法描述，RRT算法每次下一节点xnear的确定都是从最靠近xrand的树节点向xrand方向延伸。而xrand是通过概率函数随机在地图上撒点得到，所以改进RRT算法的核心就是控制随机点xrand在地图上的落点。如果能设计一种机制，使得xrand的随机性可控，即期望它下一次落点能够帮助RRT算法更快朝着目标探索，那么就可以有效提高RRT算法的效率。当然，这种控制xrand随机落点的行为会导致RRT算法丢失随机性的特点，所以改进机制需要在帮助RRT提高探索效率的同时，还要尽可能保留其随机性的特点，也就是改进RRT算法可以选择牺牲少部分随机性特点，来换取其具有一部分目标导向性的特点。

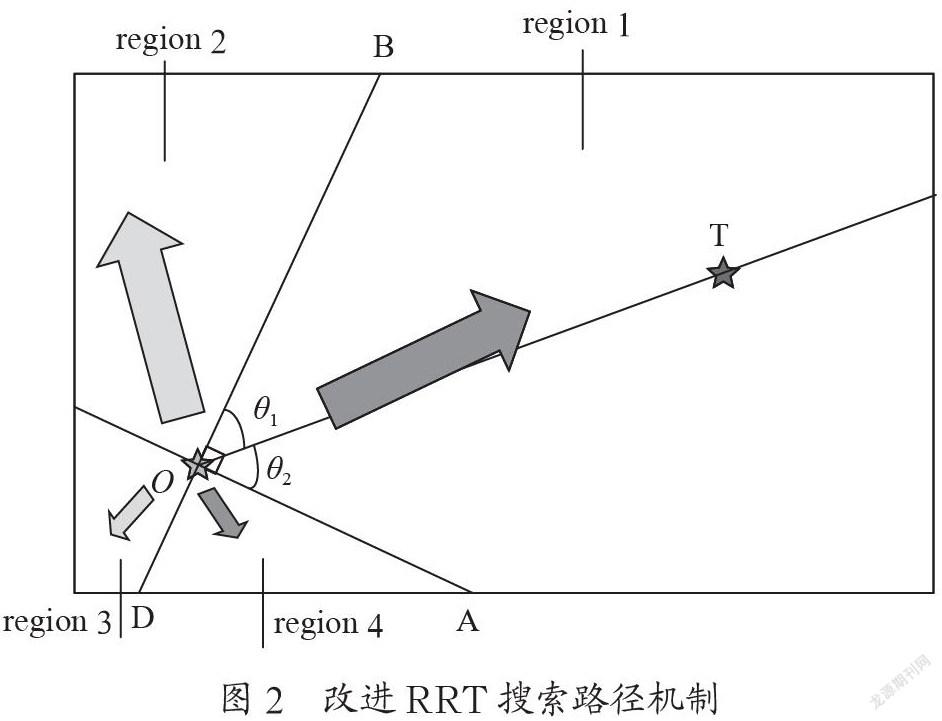
改进RRT的地图探索机制如图2所示，绿色五角星表示RRT节点树中距离目标点最近的节点，红色为目标点。以两点为中线（θ1=θ2=45°），按图示意将地图分为OAB、OBC、OCD、ODA四个区域，其中，∠AOB=∠BOC=∠COD=∠DOA=π/2。OAB为目标域，OBC和ODA为邻域，OCD为目标反向域。

设总概率不变，改进后的RRT算法将通过概率函数增大在目标区域选择xrand坐标的概率，减小在目标反向域选择坐标的概率，而xrand在两个邻域落点的概率保持不变。这样改进后的RRT算法，牺牲了一定的随机性，添加了一定的目标导向性，即树的生长被指定了大致的方向。

2.2  改进RRT的xrand节点的选取

改进的RRT算法与未改进的RRT算法比较，其他算法步骤不变，只更改随机点xrand选取的方法[6]。在原始RRT算法中，xrand的选取机制是以地图的长和宽为基础各乘以一个随机的百分比得到地图上的随机点，改进后的RRT算法在为xrand选取随机点始终是以O点建立的极坐标选取的，原始的方法并不适用。因此，改进的方法是先以O点建立一个极坐标系并求出角度和距离，随后将极坐标值转换成原全局地图上的坐标值，随后再加上O点的坐标值即可表示出xrand在全局地图下的坐标点。

首先是xrand角度的选取，角度选取机制如下：

（1）遍历当前已存在的树的节点，找出距离目标点最近的节点，记为O点;

（2）O点水平向右延伸，至地图边缘形成OE线段，以OE线段为极轴建立极坐标系;

（3）根据图2展示的改进RRT探索机制，利用概率函数分配xrand在对应区域出现的概率;

（4）概率函数执行，得到xrand的角度值。

在选取了角度之后需要对xrand节点选取长度。为了让xrand能够覆盖地图所有区域，需要对不同角度xrand长度选取做计算，xrand的长度根据可表示为：

式中rand（）为随机百分比函数，OVn他表示了O点到四个顶点其中一个的距离，若长度超出地图边界时，算法重新执行式（1），直至长度不会超出地图。OVn为xrand取不同角度时应取得的最长模长，如图3所示改进RRT中xrand长度选取机制，图中OE、OF、OG和OH将地图分为四个部分，每个部分最长的模长即为O点至其斜边的距离。设式（1）中xrand取得的角度为θ，若θ∈[0，π/2]，则n为2;θ∈[π/2，π]，n为3;θ∈[π，3/2π]，n为4;θ∈[3/2π，2π]，n为1。

在xrand以OE为极坐标系时的角度和距离都确定情况下，设O点在地图上的坐标为（xo，yo），则xrand在地图上的坐标可表示为：

式（2）表示在全局地图坐标下xrand的坐标，改进RRT算法相对于原始RRT算法需要对表1算法第三点xrand←RANDOM_NODE（Wfree）修改为本节所描述算法，其他步骤不变。

3  实验仿真

在一个20×20的方形地图内，左上角坐标为（0，0），右下角坐标为（20，20），地图中有障碍物若干，其中还包含一个凹型障碍物陷阱。RRT算法探索的起始点是（5，0），在地图中以绿色光点标明，目标点是（5，20），在地图中以黄色光点标明。在matlab上基于上述地图对原始RRT算法和改进后RRT算法进行实验仿真。

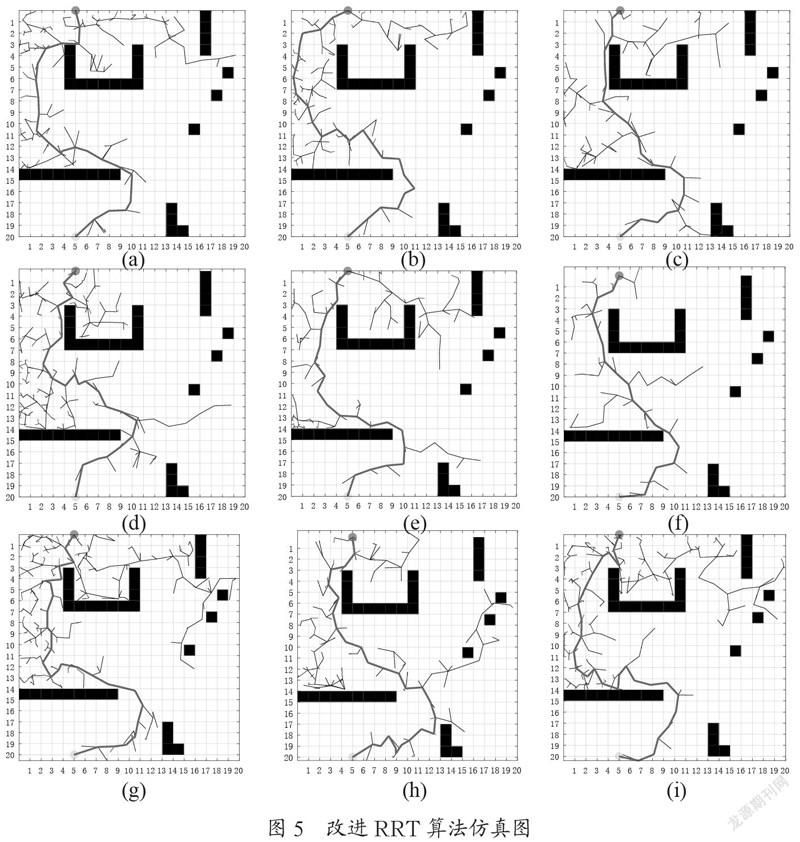
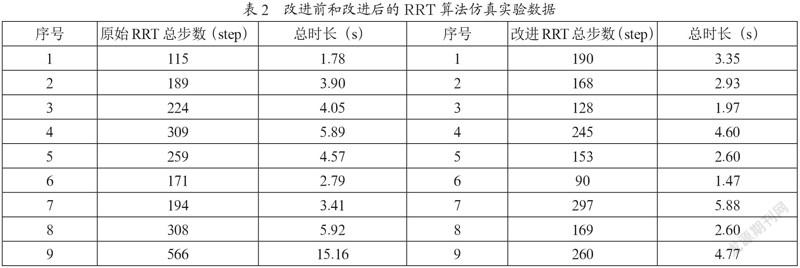
如图4所示进行了九次原始RRT算法仿真，如图5所示进行了九次改进后RRT算法仿真。表2为前后两次仿真实验相关数据。

从图4和图5可以看出，图4中的实验每次总是试图探寻整个地图以发掘找到目标点的路径，图5中的实验明显减少了对不必要搜索区域的探索。但是这种对比不是绝对的，原始RRT算法也可能比改进后RRT更先更快探索到目标点，如图4（a）对比图5（a），图4（g）对比图5（g），但是大概率对比，改进后的RRT是优于原始RRT算法的，如其余七幅图的对比。

如表2所示，原始RRT算法平均每次的总时长为5.27 s，平均每次步数为259步，改进后RRT算法平均每次总时长为3.34 s，平均每次为步数189步。表2数据表明改进后的RRT算法在平均步数和平均用时上大大少于原始RRT算法，并且他继承了原始RRT算法随机性的同时也吸收了A*和D*算法深度优先性的特点。

4  结  论

路径规划是机器人应用中非常重要的一环，本文对全局路径规划中的几种常见的路径探索算法的优缺点进行了归纳总结，最后用RRT算法结合A*和D*算法的优点进行了改进，让RRT算法既有随机性又有目标导向性，实验证明这种改进方式能利用随机性帮助智能体逃离局部最优的同时，也能更快速探索出通往目标点的路径。

改进后的RRT算法依然存在不足：

其一，对于目标区域、邻域和目标反向域的xrand落点概率值并没有严格的算法支持，在本文中依靠的是多次试验获得的相对较优的经验值，后续的改进中可以利用自适应等算法锁定最优概率值。

其二，如图5改进的RRT部分实验展示（图5（d），图5（g），图5（h），图5（i）），在牺牲了一部分的随机性之后，这可能会导致算法在大概率情况下会尝试目标方向的路径探索，即使目标方向会有障碍，这将导致一些不必要的探索出现，此时路径探索会变得集中，后续的改进中仍需要减少这种不必要的路径探索。

其三，改进后RRT算法中xrand的最长模长选取机制不是很合理，有时随机长度可能会超出地图边缘，这时xrand的长度需要重新选择，这使得改进后RRT算法的总用时可能会加长，后续改进中可以选择新的模长选取机制，以减少总时长。

参考文献：

[1] 张捍东，郑睿，岑豫皖.移动机器人路径规划技术的现状与展望 [J].系统仿真学报，2005（2）：439-443.

[2] 张海涛，程荫杭.基于A*算法的全局路徑搜索 [J].微计算机信息，2007（17）：238-239+308.

[3] 谷润平，崔朋，唐建勋，等.基于D*算法的场面滑行动态规划研究 [J].科学技术与工程，2015，15（1）：315-319+328.

[4] DU M B，MEI T，CHEN J J，et al.RRT-based Motion Planning Algorithm for Intelligent Vehicle in Complex Environments [J].Robot，2015，37（4）：443-450.

[5] 张捍东，陈阳，吴玉秀.未知环境下移动机器人实时路径规划 [J].计算机工程与应用，2018，54（19）：140-146.

[6] 刘永红，刘明雍，谢波.航位推算组合导航系统在线标定技术 [J].中国惯性技术学报，2015，23（4）：434-437.

作者简介：郭孝坤（1997—），男，安徽马鞍山人，硕士在读，研究方向：路径规划;吴玉秀（1982—），男，汉族，河南安阳人，讲师，博士，研究方向：机器视觉与图像检测;李景（1997—），男，安徽六安人，硕士在读，研究方向：双目视觉;程瑞嘉（1997—），男，山东滨州人，硕士在读，研究方向：深度学习。