截齿滚动掘进冻土过程的影响因素数值模拟研究

张将令， 李小二， 陈新明， 焦华喆， 李振华

（1.河南理工大学土木工程学院，河南焦作 454150； 2.焦作煤业集团，河南焦作 454002；3.煤炭安全生产与清洁高效利用省部共建协同创新中心，河南焦作 454150）

0 引言

随着矿井建设不断发展，人工冻结法（artificial ground freezing，简称AGF）被广泛运用到特殊矿井建设当中，解决建井深度大、冲积层厚度大等问题[1-2］。众所周知，冻土是一种特殊四相体，由固、液、气、冰晶体组成，四相物质之间相互连接，特别是冰晶体的存在使冻土强度大幅度提高[3］。冻结土层强度高、韧性大，很难挖掘，目前大部分冻土的开挖采用热融法、爆破法、人工或机械开挖等办法[4-6］。

热融法是采用电加热的方式，将电能转化为热能使冻土融化。该方法效率低且耗时长，不符合矿山能源经济建设发展理念[7-8］。爆破法在竖井下应用作业，虽然效率高、破掘冻土效果明显，但危险系数大，不利于安全施工[9-12］。人工法是由工人手持风镐进行，施工进度慢且耗费大量人力，使得整个井筒建设工作较为缓慢，影响矿井建设的工期。机械法是采用常规机械冲击破坏、截齿切削等方式开挖冻土，通过理论分析建立典型截齿滚动力学模型，研究得出截齿滚动掘进破碎是冻土开挖的主要方法[13-16］。机械冲击破坏在材料脆性越明显时破碎效率越高，广泛应用于冻结岩土破碎及煤矿开采，而滚动侵入破碎相较于冲击破碎方式有更好的适应性[17］。有学者[18］通过多功能自动控制冻土切削实验室，得到截齿与冻土相互作用数学模型，以此优化截齿的几何参数和切削速度、角度、切削量及宽度等动态参数。通过数值模型和优化的截齿应用在环链式挖掘时，发现冻土破坏效果不明显[19］。相关试验结果表明，截齿切削冻土时随着切削速度的提高，切削阻力和单位切削阻力有明显下降，冻土挖掘效率可明显提高[20-21］。还有学者利用改进的SHPB 装置测试了不同温度和应变速率下冻土的动态力学性能，提出了损伤动态本构模型[22-24］，冻土破坏的快慢与应变速率的增加有关。通过直径为50 mm 的常规分离式霍普金森压杆，得到冻土内部的裂纹分布对其在动荷载作用下的力学性能和耗能特性有显著影响，其中动态能量耗散是重要的工程设计参数，与寒冷地区冻土的破碎效率密切相关[23］。

国内外对于截齿滚动破碎冻土的研究较少，甚至没有独创性的机械用于竖井冻土的开挖运输，特别是截齿在不同侵入深度下滚动破碎冻土的仿真模拟更是鲜有涉及，大部分是研究爆破技术在人工冻结法竖井下的应用[25-27］，采用机械开挖冻土的方法几乎没有。为了解决选取最优截齿侵入深度提高冻土开挖效率的难题，本研究采用霍普金森压杆试验，结合HJC 压缩损伤模型原始参数，最终优化得到冻土本构模型参数。利用HyperMesh、LS-DY⁃NA 有限元仿真模拟得到冻土破坏过程和相关比能、总能、沙漏能等数据，确定最优截齿侵入深度，提高冻土开挖效率，对竖井更大深度的开采和建设有重要指导意义。

1 截齿滚动掘进冻土模型的建立

由SolidWorks 三维软件建立截齿滚动掘进冻土的模型，其中截齿滚动掘进冻土模型的主要特征采用1∶1 比例，便于数值模拟数据的准确性。其中HJC 动态损伤模型主要适用于压缩损伤模型，应用于冻结黏土这种脆性材料。SolidWorks软件保存模型后输出STEP 格式的文件，导入HyperMesh 有限元软件中进行参数化定义。冻土模型四周施加非反射边界条件，真实模拟冻土内部应力传播[28］。冻土动态损伤本构模型添加体积失效准则，施加Sur⁃face to Surface 接触，类型为Eroding，失效应变类型fs取0.004。为了仿真模拟的准确性，截齿滚动掘进冻土模型均采用精细化划分网格的方法。冻土网格划分为六面体，网格数量为792 000 个，截齿划分为四面体，网格数量为18 519 个。HyperMesh 软件赋予截齿模型不同的深度，给滚筒施加水平速度、旋转速度等参数，如图1 所示。最后由HyperMesh软件保存并输出K 文件，导入LS-DYNA 有限元软件中求解，得到最终数值模拟结果。滚动截齿滚动掘进冻土可以看作单截齿循环掘进冻土的过程，截齿依靠上部机架重力和主要滚动力、法向力滚动掘进冻土，最终冻土发生凹陷破坏。

图1 截齿滚动掘进冻土模型Fig. 1 Model of frozen soil excavation by cutting pick rolling

2 截齿和冻土模型的参数设置

HyperMesh软件对材料参数进行设置。截齿采用合金钢材质，密度为7 900 kg·m-3，弹性模量为270 GPa，泊松比为0.3。冻土取自矿井下黏土材料，采用土壤筛、振动台、保温箱等试验用具配置成含水率为23.87% 的颗粒级配土，用模具制作50 mm×25 mm 的试样，在-20 ℃下恒温储存为冻土。根据冻土单轴压缩试验，确定冻土静态抗压强度f′c取9.0 MPa；劈裂试验测得冻土抗拉强度T为0.3 MPa；依据霍普金森压杆冲击试验，结合HJC 原始模型参数，得到相关强度参数：A、B为归一化强度，可以改变波形峰值的大小。N、C分别为压力硬化指数和应变率系数，N可以改变峰值大小和脉冲宽度，C可以改变应变率的结果。根据这些参数的特殊性及相关文献、试验的结果，确定A=1.2，B=0.5，C=0.012，N=1.0。最终优化得到冻土本构模型参数[29-31］。

霍普金森压杆装置主要包括子弹、入射杆、透射杆、缓冲装置，以及数据采集系统，如图2 所示。在入射杆与透射杆之间放入冻土试样。

图2 试验仪器及试样Fig. 2 Test instruments and samples：Hopkinson pressure bar（a），data acquisition system（b）and frozen soil sample（c）

实验分为四组，对直径为50 mm，高度25 mm的 冻 土 试 样 在0.2 MPa、0.3 MPa、0.4 MPa、0.5 MPa 高压下进行冲击加载实验，即对应不同的冲击加载应变率600 s-1、700 s-1、900 s-1、1 100 s-1。

如图3所示，冻土随着应变率的越来越大，破碎程度越严重，碎块数目越多。冻土的破坏是由子弹

图3 冻土试样的破碎状态Fig. 3 Broken state of the frozen soil samples

根据实验数据结合式（4）~（6）优化冻土其他强度参数，得到冻土的抗压强度f′c和应力σ、应变ε̇、应变率ε̇0等试验数据。优化后的冻土本构模型参数如表1所示。

表1 冻土本构模型参数Table 1 Parameters of the frozen soil constitutive model

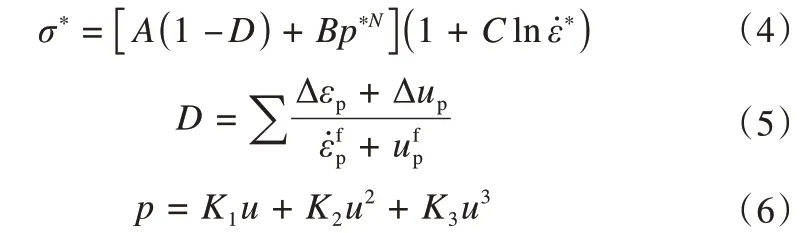
式中：A、B为归一化强度；N、C分别为压力硬化指数和应变率系数；σ*=σ/f′c，为归一化等效应力，是真实等效强度与准静态单轴抗压强度之比；p*=p/f′c，为归一化静水压力；ε̇*为真实应变率除以参考应变率ε̇0得到的无量纲应变率；D为损伤因子；Δε̇p为等效塑性应变增量；u为体积应变；Δup为塑性体积应变增量；ε̇fp和ufp分别为常压下冻土破碎时等效塑性应变和塑性体积应变；p为静水压力；K1、K2和K3为材料常数。

3 截齿掘进冻土的影响因素分析

3.1 新型重力式竖井掘进机及截齿受力分析

新型重力式竖井掘进机（图5）是一种专门在竖的冲击速度决定，子弹冲击速度越快，冻土破坏越严重。

图5 新型重力式竖井掘进机Fig. 5 A new gravity shaft excavation machine

基于弹性应力波理论和均匀应力假设，由式（1）~（3）计算得到冻土应力-应变曲线[32-35］，如图4所示。

图4 冻土应力-应变曲线Fig. 4 Stress-strain curves of frozen soil：stress curves（a），strain curves（b）and stress-strain curves（c）

式中：ε̇I(t)、ε̇R(t)和ε̇T(t)分别为入射波、反射波和透射波；E0、A0和C0分别为钢杆的杨氏模量、横截面积和弹性波速；As和Ls分别为冻土试样的横截面积和高度；t为弹性波的持续时间。井井筒内破碎冻土的设备，该机械包括掘进机构、行走机构等。设计紧凑，创新性将掘进机构与行走机构合二为一，掘进机可以滚动掘进冻土的同时按指定路线行走、转弯，便于在竖井空间下灵活应用施工，对竖井下冻结壁稳定性不会产生影响且安全高效，可解决竖井下冻结土开挖难度大、人工挖掘效率低的问题。设备利用截齿连续滚动向下、行走式掘进冻土，截齿掘进冻土预定深度后，行走机构推动掘进机进行下一阶段滚动掘进冻土。

为了研究截齿滚动掘进冻土能力，对截齿插入冻土过程进行受力分析。其中截齿长度103 mm，外形为圆锥体，便于冻土受到集中应力而发生剪切及拉、压侵入破坏。滚筒直径为580 mm，多个截齿等间距布置在滚筒上。截齿刚开始作用到冻土时受到侧向力Fy、法向力Fz；当滚筒加速旋转时截齿以不同角度θ滚动侵入冻土内部，冻土主要受到滚动力Fx和法向力Fz，包括旋转惯性力Fr=Mrω2和上部机架重力和自重。其中，M为滚筒-截齿质量，r为滚筒质心到截齿尖端的距离，ω为角速度（rad·s-1），如图6所示。

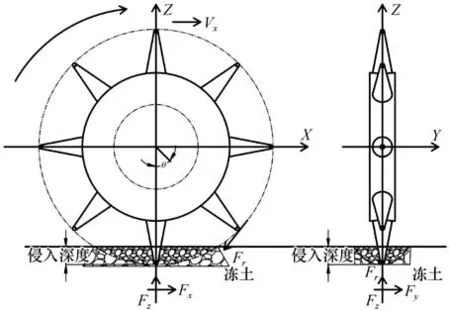
图6 截齿受力分析Fig. 6 Force analysis of the cutting picks

基于现场实际，对截齿侵入深度为4 cm 时进行冻土损伤过程数值模拟，便于分析冻土内部应力、应变和截齿三向力变化规律。掘进机开始滚动掘进冻土时，截齿滚动力、法向力增大，冻土破坏区域应力最大；当冻土发生扰动破坏后不需更大的作用力，故应力呈波纹式向下递减。其中，法向力Fz是冻土裂纹扩大的主要影响因素。冻土与截齿接触的部位有单元缺失、色泽集中和黑色条纹连续传播至远处等现象，说明冻土发生一定深度的凹陷破坏，产生众多细小的裂纹，凹陷破坏区域应力最大，应力呈波纹式向下递减至0，如图7（a1）~（a2）所示。当截齿再次掘进到未破坏冻土时，滚动力Fx、法向力Fz逐渐增大，完全满足冻土抗压、拉破坏强度要求。黑色条纹主要分布在作用区域下方，多处单元缺失附近产生的色泽较明显，说明冻土破坏应力范围变大、凹陷面积增加，裂纹延伸至底部，冻土再次发生压、拉剪破坏[36-37］，如图7（b1）~（c2）所示。

截齿持续滚动掘进冻土时，冻土有明显色泽块和波纹分界线、单元缺失区域变大，单元块随着截齿的滚动脱离冻土，黑色条纹互相连接，说明冻土内部应力更大，发生大面积的凹陷，冻土结构互相分离，有更多的主裂纹形成，如图7（d1）~（d2）所示。图中a、b、c、d 段分别指的是应力云图上的水平缺失部位，即截齿滚动掘进冻土的水平距离。

图7 截齿滚动掘进冻土循环过程Fig. 7 Circulation process of frozen soil excavation by cutting pick rolling：destruction of frozen soil in Section a（a1），cross-section destruction in Section a（a2），destruction of frozen soil in Section b（b1），cross-section destruction in Section b（b2），destruction of frozen soil in Section c（c1），cross-section destruction in Section c（c2），destruction of frozen soil in Section d（d1）and cross-section destruction in Section d（d2）

由于截齿在预定深度下滚动破坏冻土，冻土密实结构已经扰动，但还未发生破坏，故截齿开始滚动时截齿滚动力Fx、法向力Fz瞬间增大至逐渐减小，说明冻土发生凹陷破坏。当截齿再次连续滚动到应力变化、已发生塑性破坏的区域时，滚动力Fx、法向力Fz达到峰值后开始下降，这与截齿连续行走式、向下滚动的特点有关。截齿侧向力Fy与截齿形状、侵入深度和冻土内摩擦角有关，与冻土拉、压破坏影响不大，故不作考虑，如图8所示。

图8 截齿侵入深度为4 cm时三向力的变化Fig. 8 Changes of three-dimensional force under the cutting pick invasion depth of 4 cm

3.2 不同侵入深度下冻土破坏及截齿三向力变化

根据现场实际，暂设定单截齿破冻土深度为5 mm·c-1（c 为滚筒旋转圈数）进行模拟分析。主要分析截齿在不同侵入深度下掘进冻土，得到冻土破坏特征和冻土应力、应变变化过程，分析比能、总能等能量曲线，确定最优截齿侵入深度，如图9（a）所示。

截齿开始滚动时，冻土同时受到滚动力、法向力和侧向力而产生裂纹，冻土发生弹性-塑性的破坏，随着增加截齿侵入深度，冻土应力区域向下扩展、凹陷面积增大，冻土碎块变多，发生明显的压、拉剪破坏。冻土在截齿侵入深度为2 cm 时，作用区域及接触部位出现缺失、脱落的单元块和众多的黑色条纹，色泽明显且向下呈波浪式变浅，说明冻土受到截齿滚动力、法向力后发生压、拉破坏，冻土产生裂纹、碎土块和凹陷破坏。如图9（b）所示。

截齿向下滚动掘进冻土内部3~6 cm 时冻土产生较多飞溅的单元块，截面单元缺失区域和色泽变化范围扩大，黑色条纹变密且向底部延伸，说明随着截齿掘进冻土深度越来越大，冻土小裂纹逐渐扩张为主裂纹，冻土发生塑性-密实性变形的破坏过程，碎块变多且细小，这与截齿靠重力连续滚动特征相关。冻土凹陷破碎面积增大，应力呈波纹式扩展至底部区域，整体结构出现应力变化，裂纹扩大使冻土发生大变形和结构错动，冻土发生破碎破坏。如图9（c）~（f）所示。

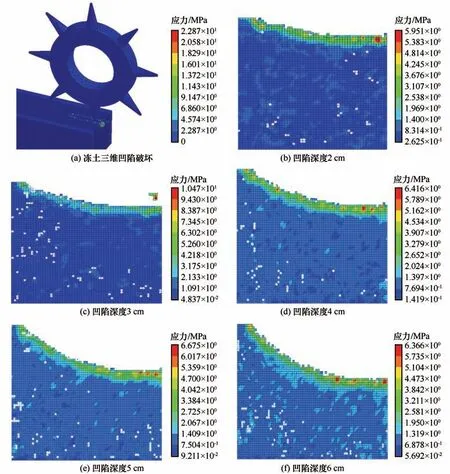
图9 不同侵入深度下截齿掘进冻土Fig. 9 Frozen soil excavation by cutting picks under different invasion depths：three-dimensional destruction of frozen soil（a），depressed depth of 2 cm（b），depressed depth of 3 cm（c），depressed depth of 4 cm（d），depressed depth of 5 cm（e）and depressed depth of 6 cm（f）

与此同时，随着侵入深度的增加，截齿滚动掘进冻土的三向力呈正弦函数变化，这与截齿在不同侵入深度下连续滚动冻土有关。侵入深度越大，截齿滚动接触冻土单位面积越大，主要滚动力Fx和法向力Fz逐渐变大，冻土产生较大应力和裂纹，冻土发生破坏后截齿滚动力、法向力等主要作用力逐渐下降；当截齿连续向前滚动掘进未破坏的冻土时，滚动力、法向力等作用力又开始变大，冻土再次发生破坏，截齿掘进冻土的三向力随着冻土的破坏呈先增大后变小的变化规律，如图10所示。

图10 截齿三向力曲线Fig. 10 Three-dimensional force curves of cutting picks：Fx（a），Fy（b）and Fz（c）

考虑到截齿的连续滚动的特点，冻土碎块来不及排出而又重新被挤压，形成一个凹陷的密实核区域，冻土内部应力会产生不同的变化趋势，这与截齿侵入深度和破坏程度密切相关。当侵入深度为2~6 cm 时，冻土内部应力瞬间变大，随着截齿的连续滚动，冻土破坏程度越来越大，内部应力开始下降，应变逐渐上升，这是由于冻土发生了脆性破坏，失去了抵抗变形的强度。伴随着截齿侵入深度的增加，冻土破坏程度越大，内部应力、应变越大，而在侵入深度从2 cm增加到3 cm时冻土应力减小，应变变大，这是由于增加截齿侵入深度会加大冻土的破坏程度，冻土强度瞬间下降，故内部的应力下降，应变增大。当提高截齿侵入深度为4 cm 时，冻土内部应力、应变都开始增大，说明冻土碎块变多，破坏程度加大。同样，当提高截齿侵入深度从4 cm 增大到5 cm 时，冻土内部应力又逐渐减小，应变持续增大，说明冻土破坏程度进一步加大。当截齿侵入深度从5 cm增大到6 cm时，冻土应力、应变峰值最大，说明增加截齿掘进深度会加快冻土的破坏，冻土破坏越严重，如图11所示。

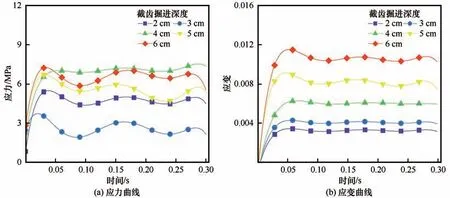
图11 冻土应力和应变模拟曲线Fig. 11 Stress（a）and strain（b）simulation curves of frozen soil

3.3 确定最优截齿侵入深度

提高截齿侵入深度，截齿滚动掘进更多单位体积的冻土时消耗更多的能量，内能逐渐上升，如图12（a）所示。随着截齿侵入冻土的深度越来越大，截齿的滚动力、法向力越大，总能逐渐上升，当冻土受到截齿连续滚动发生破坏后，截齿滚动力、法向力开始下降，总能上升趋势变缓，如图12（b）所示。

比能是破坏单位体积冻土需要做的功[38-39］（J·mm-3），是体现截齿破土效率的重要性指标。比能越小，截齿破碎单位体积冻土所需的能量越低，破冻土效率越高，如式（7）~（8）所示。

式中：SE为破冻土比能（J·mm-3）；WN为截齿作用力做功（J）；V为冻土破碎的体积（mm3）；Fx为截齿滚动力（N）；Fz为法向力（N）；Pi为截齿侵入深度（mm）；J为截齿的滚动距离（mm）；Si为冻土在不同侵入深度下的破碎面积（mm2）。一般情况下，侧向力做功为总作用力做功的5%，故只考虑滚动力和法向力做功。

随着截齿侵入深度的增加，冻土破坏程度加大，截齿滚动力、法向力没有较大提高，而冻土破碎的单位体积变大，故比能逐渐下降。侵入深度为6 cm 时比能最低，但总能耗最大。提高侵入深度从4 cm 到5 cm 时，比能出现拐点，比能变大，总能消耗提高了50%。故从整体因素考虑来看，最优截齿侵入深度为4 cm，掘进冻土效率最高且能耗低，如图12（c）所示。

另外，数值模拟中涉及到的沙漏能是至关重要的，沙漏能是一种单元的零能模式，可以加快计算速度[40］。数值计算标准规定，沙漏能小于总能量的5%时，可以认为数值模拟结果可靠。截齿在不同侵入深度下滚动掘进冻土时沙漏能远远小于总能，数值模拟结果符合要求，如图12（d）所示。

图12 截齿掘进冻土能量曲线Fig. 12 Energy curves of frozen soil excavation by cutting picks：internal energy curve（a），total energy curve（b），specific energy curve（c）and leakage energy curve（d）

4 结论

（1）新型重力式竖井掘进机利用截齿连续滚动向下、行走式掘进冻土，截齿在一定侵入深度下连续滚动掘进冻土时三向力呈先增大后减小的变化规律。掘进机开始滚动掘进冻土时，截齿滚动力、法向力等作用力逐渐增大，随着冻土破坏程度越来越大，截齿作用力逐渐减小，这与截齿的连续滚动、行走式掘进冻土的特点有关。

（2）截齿滚动掘进冻土时冻土内部应力向下无限扩展，冻土凹陷破坏区域应力最大。随着截齿侵入深度的逐渐增大，冻土破坏程度加大，应力变化范围增加，应力向下逐渐递减，直观探究冻土破坏过程及应力、应变变化。

（3）分析不同截齿侵入深度下冻土破坏面积和破碎特征，冻土破坏程度越大，截齿滚动掘进冻土的比能逐渐变小。在截齿深度为4 cm 时比能出现拐点，比能较低，为0.1 J·mm-3；结合总能、比能、沙漏能等曲线，确定在冻土单轴抗压强度为9 MPa时，截齿滚动掘进冻土过程中存在最优截齿侵入深度为4 cm，冻土破坏特征明显，截齿滚动掘进冻土效率最高且能耗低。