Nuclear mass based on the multi-task learning neural network method

Xing-Chen Ming· Hong-Fei Zhang· Rui-Rui Xu · Xiao-Dong Sun ·Yuan Tian · Zhi-Gang Ge

Abstract The global nuclear mass based on the macroscopic—microscopic model was studied by applying a newly designed multi-task learning artificial neural network (MTL-ANN). First, the reported nuclear binding energies of 2095 nuclei（Z ≥8，N ≥8）released in the latest Atomic Mass Evaluation AME2020 and the deviations between the fitting result of the liquid drop model (LDM)and data from AME2020 for each nucleus were obtained.To compensate for the deviations and investigate the possible ignored physics in the LDM, the MTL-ANN method was introduced in the model. Compared to the single-task learning (STL) method, this new network has a powerful ability to simultaneously learn multi-nuclear properties,such as the binding energies and single neutron and proton separation energies. Moreover, it is highly effective in reducing the risk of overfitting and achieving better predictions. Consequently, good predictions can be obtained using this nuclear mass model for both the training and validation datasets and for the testing dataset.In detail,the global root mean square (RMS) of the binding energy is effectively reduced from approximately 2.4 MeV of LDM to the current 0.2 MeV, and the RMS of Sn, Sp can also reach approximately 0.2 MeV. Moreover, compared to STL, for the training and validation sets, 3—9% improvement can be achieved with the binding energy, and 20—30% improvement for Sn, Sp; for the testing sets, the reduction in deviations can even reach 30—40%, which significantly illustrates the advantage of the current MTL.

Keywords Macroscopic—microscopic model · Binding energy · Neural network · Multi-task learning

1 Introduction

Nuclear mass is a fundamental quantity widely involved in various domain studies in nuclear science and engineering. Accurate masses are crucial not only to derive highly concerning nuclear shell information, but also to quantify the procedure of nuclear reactions [1—4]. Thus,much interest has been drawn in the past several decades to obtain and improve nuclear mass values to meet the requirements of contemporary nuclear studies.

Nuclear researchers have been involved in this field,especially since the 1950s, and international cooperation has been established to create the well-known atomic mass evaluation(AME)motivated to provide a reliable database to the public, where the data are based on pure measurements and empirical extrapolation [5—7]. Significant success has been achieved with AME, and over 3500 nuclei have been evaluated, whereas there is a gap between the number of evaluated nuclei and the real requirements from high-fidelity simulation calculations regarding complex nuclear physics environments. Moreover, the uncertainties of AME are still worth concentrating on, for further improvements.

Therefore, many theoretical calculations based on microscopic mean-field models [8—11] and macroscopic—microscopic models[12—21]have been developed to obtain the global nuclear mass.The macroscopic—microscopic models start from the liquid drop model (LDM) and the correction energy terms, based on a special single-particle potential, which makes the calculation relatively simple compared with microscopic mean-field models. Meanwhile, the macroscopic—microscopic models show better performance than the global nuclear mass [5, 22]; therefore, they are normally considered more applicable in real evaluations.

In the scheme of macroscopic—microscopic models, the theoretical determination of the shell correction energy of the single-particle potential is complicated [23].Normally,in real calculations, smoothing methods are necessary to deal with the single-particle potential,which influences the final results [22, 24]. To simplify this problem, a so-called‘‘simple nuclear mass formula form’’ is proposed in [25],the linear polynomial functions are applied to replace the residual correction energy and the global root-mean-square(RMS) successfully reaches 0.266 MeV compared to the original LDM of 2.456 MeV. Artificial neural networks(ANNs)have been proven to be excellent methods in many research regions [24]. It seems to be a better choice here than simple mathematical functions because of its powerful capability in dealing with complex problems.

The application of neural networks to predict nuclear masses can be traced back to the 1990s [5, 26]. The input layer of the neural networks is designed according to basic nuclear properties such as the proton,neutron number Z,N of target nuclei, and the relevant Z0, N0of the nearest magic number, and the application of ANN in mass model calculations has been validated by many perfect outputs.Most previous studies on the ANN nuclear mass were constructed using the single-task learning (STL) technique at the output layer,where the fluctuation of nuclear binding energy（δLDM）was taken as the only task guiding the entire training and testing procedures. Consequently, a better global RMS is obtained via STL; for example, the RMS can be reduced to 0.235 MeV in Ref. [24]. Other nuclear properties such as the single proton separation energy（Sp）,single neutron separation energy（Sn）,nuclear charge radii,and β-decay half-lives have also been studied using various artificial intelligence (AItools [27—31]). In most of the above-mentioned studies, AI methods are trained to learn one of the nuclear properties. The aforementioned properties are naturally correlated;therefore, novel AI methods that can study more than one property simultaneously should be developed.Accordingly,we attempted to involve more tasks in the ANN to study the neural network using deep learning and further reduce the global RMS.

In this study, an improved multi-task learning (MTL)technique was created to integrate more crucial knowledge from nuclear physics into the neural network. A total of 2095 nuclei with fully evaluated nuclear properties in the AME were adopted in this new MTL-ANN. To include more tasks, Snand Spare included to provide information on the nuclear shell. In the input layer, we adopt the neurons with proton number,mass number,and the number of residual particles or holes relative to the closet magic shell for protons, and that for neutrons, which were applied in our previous study [24]. Moreover, we expand the current input layer by adding pairing terms with the expression in Ref. [18].

The remainder of this paper is organized as follows. In Sect. 2, first, a general LDM formula is used, and the general formalism and structure of the present applied neural network with the MTL technique, called MTLANN, are introduced, and a new mass method incorporating MTL-ANN is proposed. The results of the global analysis of 2095 nuclear binding energy with the novel MTL-ANN are presented in Sect. 3, and discussions on MTL-ANN parameters and optimizing procedures are illuminated in detail simultaneously. Finally, the summary of this study is provided in Sect. 4.

2 Macroscopic-microscopic model with multi-task

learning technique In the macroscopic—microscopic model scheme, the binding energy of a given nucleus with A mass and Z protons E(Z, A) can be assumed as the macroscopic binding energy with LDM ELDM（Z，A） and the fluctuating part δLDM（Z，A） [32],

where the coefficients of volume energy aV,surface energy aS, and pairing energy apaircan be adjusted to determine ELDM（Z，A）; VCis the Coulomb energy expressed as VC=（aC（Z（Z-1）））/（A1/3（1-Z-2/3）） [13], where aCis the adjustable parameter; and asymis the coefficient for the symmetry energy parameter, which is taken as

In this study, to determine the macroscopic—microscopic ELDM（Z，A）, the nuclear properties binding energy (EAME),Sn, and Spof 2095 nuclei （Z ≥8，N ≥8） within AME2020 were adopted to restrict the free parameters.The optimized coefficients were obtained as aV=15.6829 MeV,aS=-18.5264 MeV, apair=6.5149 MeV,aC=-0.7170 MeV, csym=46.4121 MeV, and κ=-0.6460, and the current LDM RMS deviation was 2.4027 MeV.

Conversely, the fluctuating part of the binding energy（δLDM） is a necessary compensation in the macroscopic—microscopic model.Multi-task learning has a strong ability to improve generalization using the domain information contained in the data, and the learned knowledge for one task can assist other tasks to be learned better [33].Therefore, a novel MTL artificial neural network (MTLANN) was designed in this study to mimic δLDMmore accurately using more related nuclear properties.

The MTL-ANN is a feedforward neural network. The structure of the MTL-ANN used in this study is shown in Fig. 1; the architecture consists of three layers: input,hidden, and output.

Fig. 1 (Color online) Structure of the present MTL-ANN

Five features （Z，A，｜Z-Z0｜，｜N-N0｜，δnp） are taken as the inputs, where Z, N, and A are the proton number,neutron number, and mass number of a given nucleus,respectively; Z0and N0are suitable magic numbers,assumed as 8, 20, 50, 82, and 126 for protons, and 8, 20,50, 82, 126, and 184 for neutrons, and δnpis the value in Eq. (4) used to describe nuclear pairing and shell effects.

As shown in Fig. 1, two hidden layers were defined to adequately share information, and 20 neurons were set in each hidden layer. The multi-task outputs are obtained through training iterations between the hidden and output layers back and forth. Generally, it is assumed that the input vector is x=（x1，x2，...，xn）, the obtained output vector is y=（y1，y2，...，ym）, and n, m denotes the total number of inputs and tasks.The lth task ylcan be written as

where （al，ck，ej）, and （blk，dkj，gji） denote the optimized bias and weight parameters for neurons between different layers;H1and H2are the number of neurons in each hidden layer. The optimized parameters are obtained through iterations for net training to obtain the minimized value of a defined loss function L in each iteration. For the ith iteration, Lican be expressed as

In this study, three types of task were adopted to train the network. First, according to the experimental values from AME2020[6, 7]and the theoretical results from LDM, TBcan be obtained as:In addition to TB, two other properties related to nuclear mass, neutron, and proton separation energies Snand Spin AME2020 are adopted as two choices for the current multiple tasks.Similar to Eq. (9),their target values can be obtained as Tsnand Tsp. Consequently, in the real network training process,four task groups:1)TB,2)TBand Tsn,3)TBand Tsp,and 4)TB,Tsnand Tspare classified to compare the effects of different types of data in AME2020.

In addition, it should be noted that a hard-sharing approach is employed in all the network neurons to build the full connections between the input, hidden, and output layers, which is believed to contain more nuclear mass physics in the training process and efficiently avoid overfitting [34]. Moreover, the limited-BFGS, an updated quasi-Newton method that can deal with large-numberparameter training [35], is used in backpropagation learning procedures to efficiently obtain the minimum loss value.

3 Result and discussion

The newly designed MTL-ANN for the nuclear mass was used to analyze 2095 nuclei （Z ≥8，N ≥8） from the AME2020 database. In our calculation, 2095 nuclei were divided into three datasets for training, validation, and testing. All the data were sampled with a uniform distribution. In practice, 95 nuclei were first sampled from the data pool, which did not participate in neural network training. Subsequently, 1400 nuclei of training data were constructed by sampling stochastically from the remaining 2000 nuclei, and the remaining 600 nuclei were used for validation.

Fig. 2 Variation of loss values with the iterations in training and validation. The solid line indicates the loss in training for the multitasks (TB TSn and TSp) of 1400 nuclei; the dashed line is the derived loss of 600 nuclei in validation using the trained network

In our training process, the loss value can normally reach stable values after several hundred iterations. The convergence for data training is shown in Fig. 2. The loss for training reached a minimum after 200 iterations, and the corresponding validation value maintained a speed similar to that of the training.The stability of the two main procedures guarantees the correctness of the network.

To examine the validity of the proposed model, four types of network were designed according to the tasks in the output layer. The RMS values of the binding energies（EMTL）, neutron separation energy （Sn）, and proton separation energy （Sp） in the training, validation, and testing processes are listed in Table 1. The RMS is calculated as

where Eexpand Ecalcindicate the experimental data and calculated results,respectively,and N is the total number of points of concern.

Compared to the simple LDM model, the RMS of the binding energy between the calculation and experimental data can be reduced sharply from 2.4027 MeV to the current of 0.2—0.24 MeV. Moreover, the multi-task networks with TYPE 2: TBand TSn, TYPE 3: TBand TSp, TYPE 4:TB,TSn, and TSpall show better performance compared to network TYPE 1: with only a single task TB, which demonstrates that the MTL approach has a more powerful capability to improve the mass model, and TYPE 3 can obtain the best RMS for the binding energy EMTLnot only in training and validation but also in the testing process.However,it can also be observed that when more tasks are added, the learning performance of the network may worsen. In TYPE 4, the RMS of the network with more tasks TB,TSn, and TSpare even larger than the RMS in TYPE 2 and TYPE 3.This is called‘‘negative transfer’’in neural network training,which may be caused by the inner contradiction of experimental information from TSn, TSp,and TBin the task inputs.

The prediction power of the MTL model is also verified in the testing part in Table 1.For the randomly selected 95 nuclei, the results predicted by the current multi-task network performed similarly to the training and validation.Moreover, when we repeated the experiment by changing the 95 test sets, the change in Table 1 could be ignored because of its small percentage.In conclusion,TPYE 3 can suitably improve the current mass model more than other models.

To investigate further, we compare Snand Spwith the related experimental data in Figs. 3, 4, 5, 6, 7, 8, 9, 10 for the selected nuclear chains Z =8，22，61，84 and N =8，22，61，84, and the absolute deviations between the calculations and experimental data for δSnand δSpare plotted for each concerned nucleus. From these figures for each nucleus, the model description of Snand Spcan be observed are satisfying, and it can also be confirmed thatall current MTL networks can better describe the nuclear mass compared to STL.The four types of MTLs almost fit the experimental data analogously, although the global RMS of EMTL, Sn, and Sptesting shows that the TPYE 3 task group (TBand Sp) are the best choices.

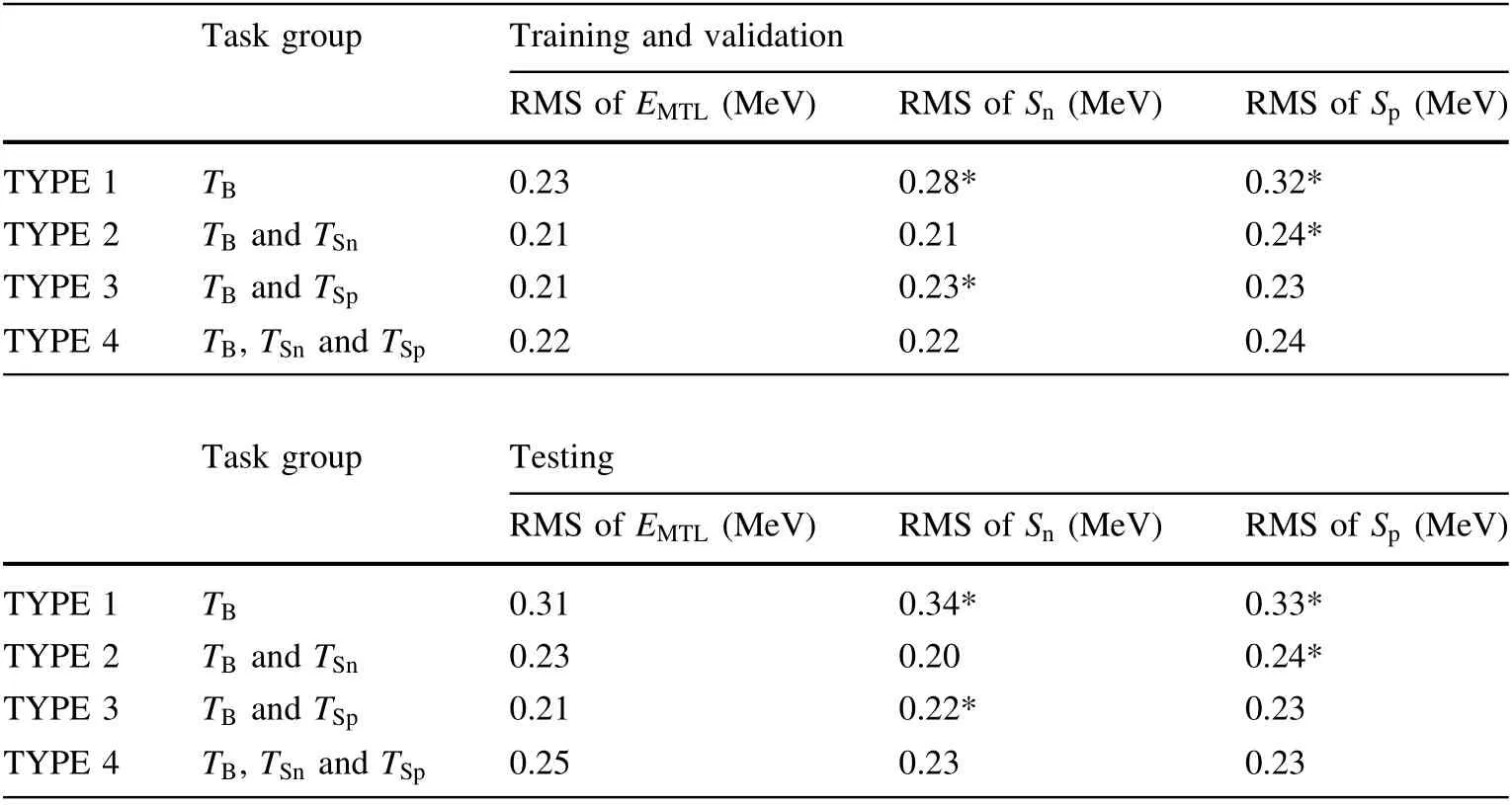
Table 1 RMS of experimental data and MTL method results

Fig.3 (Color online)Left panel:the single neutron separation energy from the results of different networks and experimental value for Z =8.Right panel: Sn error values for the corresponding nuclei on the right

Fig. 4 (Color) Same as Fig. 3 but for Z =22

For different nuclear mass regions, it can observe that the prediction ability for the corresponding nuclei is significantly improved with increasing Z and N. The absolute values of δSnand δSpare varied from approximately 1.0 MeV for the very light nuclei (Z =8，N =8) to approximately 0.2 MeV for the heavy nuclei, which illustrates the obvious better fittings for the heavier mass region.

Fig. 5 (Color) Same as Fig. 3 but for Z =61

Fig. 6 (Color) Same as Fig. 3 but for Z =84

Fig. 7 (Color) Left panel: the single proton separation energy from the results of different networks and experimental value for N =8. Right panel: Sp error values for the corresponding nuclei on the right

Fig. 8 (Color) Same as Fig. 7 but for N =22

In addition, the current predictions of the network are significantly influenced by the status of the reported data in AME2020.For example,in the case of Z =61,some large vibrations occur abnormally within the N =90—93 scope because the regulated patterns of the experimental data of N =90—93 visibly deviate from those of other neighbor nuclei.We also investigated the reported errors in this mass region.As observed,the current predictions from MTL are populated beyond the experimental error band, that is, the data for Z =61 and N =90—93 are recommended in AME2020 as 5.604±0.02 MeV, 7.860±0.02 MeV,5.939±0.03 MeV, and 7.465±0.03 MeV; however, the deviations of our MTL-related predictions all reach approximately 0.4 MeV as shown in Fig. 5. These large inconsistencies between the experimental data and model predictions require more attention to investigate the correctness of the measured points and our models in the future.

Fig. 9 (Color) Same as Fig. 7 but for N =61

Fig. 10 (Color) Same as Fig. 7 but for N =84

4 Conclusion

In summary, a newly designed MTL-ANN method was introduced to the global macroscopic—microscopic mass model. This method has been proven to increase the accuracy of mass models and effectively reduce the risk of network overfitting.

Five essential nuclear properties related to the neutron number, mass number, near magic number, and pairing（Z，A，｜Z-Z0｜，｜N-N0｜，δnp） were adopted as inputs to involve the nuclear shell and odd-even information in the present model. Three types of multi-task networks related to the nuclear binding energy,Snand Sp,are systematically investigated, and 2095 nuclei in AME2020 with the full nuclear properties above are selected in the network. All three designed multi-task networks can describe the experimental data of the nuclear binding energy,Snand Spanalogously from the light to the heavier nuclei.The global RMS deviations of the binding energy of the LDM can be significantly reduced by MTL-ANN,and MTL-ANN under the （TB，TSp） task appears to be a better choice for the others.Moreover,compared to the STL method,significant improvements can be observed in the training and validation processes, even in the testing process, where the reduction in deviations can reach 30—40%.

All of these excellent results verify the impressive prediction capability of the MTL-ANN mass model, which implies good predictive performance in the known nuclear region. Moreover, it can provide important hints to examine the correctness of the experimental data available in the future.

Author’s contribution All authors contributed to the study conception and design.Material preparation,data collection,and analysis were performed by Xing-Chen Ming.The first draft of the manuscript was written by Xing-Chen Ming, and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.