Iterative Bayesian Monte Carlo for nuclear data evaluation

Erwin Alhassan· Dimitri Rochman · Alexander Vasiliev · Mathieu Hursin,3 ·Arjan J. Koning · Hakim Ferroukhi

Abstract In this work, we explore the use of an iterative Bayesian Monte Carlo (iBMC) method for nuclear data evaluation within a TALYS Evaluated Nuclear Data Library (TENDL) framework. The goal is to probe the model and parameter space of the TALYS code system to find the optimal model and parameter sets that reproduces selected experimental data. The method involves the simultaneous variation of many nuclear reaction models as well as their parameters included in the TALYS code. The‘best’ model set with its parameter set was obtained by comparing model calculations with selected experimental data.Three experimental data types were used:(1)reaction cross sections, (2) residual production cross sections, and(3) the elastic angular distributions. To improve our fit to experimental data,we update our‘best’parameter set—the file that maximizes the likelihood function—in an iterative fashion. Convergence was determined by monitoring the evolution of the maximum likelihood estimate (MLE)values and was considered reached when the relative change in the MLE for the last two iterations was within 5%. Once the final ‘best’ file is identified, we infer parameter uncertainties and covariance information to this file by varying model parameters around this file. In this way, we ensured that the parameter distributions are centered on our evaluation.The proposed method was applied to the evaluation of p+59Co between 1 and 100 MeV.Finally, the adjusted files were compared with experimental data from the EXFOR database as well as with evaluations from the TENDL-2019, JENDL/He-2007 and JENDL-4.0/HE nuclear data libraries.

Keywords Iterative Bayesian Monte Carlo (iBMC) ·Nuclear reaction models · Model parameters ·Adjustments·Bayesian calibration·Nuclear data·TALYS

1 Introduction

The use of nuclear reaction models combined with experimental data and Bayesian statistical inference has gain prominence in nuclear data evaluation, especially in the fast energy region, over the past decade or so. These techniques have been developed partly in order to overcome the assumption of linearity used with the Generalized Least Squares (GLS) methods [1, 2] used in nuclear data evaluation and also, because of the increasing availability of computational resources which now makes large Monte Carlo calculations possible. Examples of nuclear data and covariance evaluation methods based on microscopic experimental data and statistical inference include the Total Monte Carlo (TMC) method presented in Ref. [3],the Bayesian Monte Carlo [4, 5], the filtered Monte Carlo [6], the Backward—Forward Monte Carlo(BFMC) [7],the Unified Monte Carlo(UMC-G and UMCB) [8, 9], and the combination of Total Monte Carlo and the Unified Monte Carlo (TMC + UMC-B) methods presented in Ref. [10]. Successful applications of the BMC and BFMC methods with respect to integral experiments have been presented in Refs. [11—13].Also available is the Monte Carlo Bayesian Analysis (MOCABA) method which uses Bayesian updating algorithms for the adjustment of nuclear data based on integral benchmark experiments [14]. A similar approach based on Bayesian Monte Carlo which combines differential and integral experiments for data adjustment has been presented in Ref. [15].

One underlying assumption of the Monte Carlo-based evaluation methods that make use of microscopic experiments presented above is that the source of uncertainty in nuclear data is a result of our imperfect knowledge of the parameters to nuclear reaction models [7]. Therefore, it is assumed that by varying the input parameters to these models, one could improve the agreement between model outputs and carefully selected experimental data.However,comparisons between model calculations and experiments most often reveal that nuclear reaction models are still deficient and are therefore unable to reproduce experimental data. In some cases, the models appear to be completely off the experimental data available, i.e., they are not able to reproduce even the shape of the experimental data [16, 17]. An example is the59Co(p,2np)channel between 1 and 100 MeV, where large deviations were observed between model calculations and the experimental data available.One approach(assuming the models were perfect but with uncertain parameters) has been to widen the model parameter space in order to increase the likelihood of drawing parameter combinations that can better reproduce experimental data as carried out in Refs. [4, 15]. However, as observed in Refs. [10, 15],increasing the parameter space could lead to situations where a combination of model parameters are being drawn from a region of the parameter space where the likelihood is low.This normally leads to a situation where very low or insignificant file weights are assigned to a large number of the random nuclear data files produced as observed in Refs. [10, 15].

One approach has been to attribute the inability of models to reproduce experimental data to the presence of model defects and to try to incorporate these defects in evaluations in a statistically rigorous way as presented in Refs. [16, 18, 19]. In Refs. [4, 7] for example, the likelihood function was modified in order to take into account the effects of these model defects. While the efforts at including the effects of model defects into the evaluation process is very commendable, we believe that since the model space has been left largely unexplored especially with respect to proton induced reactions [17, 20], by exploring the model and model parameter space together,we can be able to identify the optimal model combinations with their corresponding parameter sets that can better reproduce available microscopic experimental data. The underlying assumption being that there is a true solution hiding in the model and parameter space which can be identified and therefore, by sampling from a rather large non-informative prior, we would be able to locate this‘true’ solution. However, we do note that there are no perfect models and hence,our‘best’models would always contain deficiencies. Therefore, the inclusion of these model defects into the method presented in this work is proposed for future work. An alternative approach for including model uncertainties would be to carry out a Bayesian Model Averaging over all or a selection of the model combinations available as proposed in Refs. [21, 22]. In Ref. [22], instead of selecting a single model combination(as in this case)and proceeding with it as if it is the true model set, we averaged over all or a selection of the models. In this way, a central file with its corresponding covariance matrix were obtained for both cross sections and angular distributions. Bayesian Model Averaging (BMA) was not carried out in this work.

The idea of this work is that once the best model and parameter combination is identified, we can improve the evaluation (the central file) by re-sampling the model parameters around this file in an iterative fashion, each time,using the previous‘best’file or evaluation as the new central file. We believe that after a number of iterations within the limits of the considered models, convergence would be reached. The convergence criterion used is the relative difference between the maximum likelihood estimates of the last two iterations. More information on the convergence criteria used has been presented in Sect. 2.4.

In this work, the proposed iterative Bayes methodology termed iBMC (Iterative Bayesian Monte Carlo) has been applied to the evaluation and adjustment of p+59Co between 1 and 100 MeV. Evaluation of proton-induced reactions on59Co is important for several reasons. First,cobalt-based alloys are used in nuclear reactors as structural materials because of their high strength and hardness properties [23]. Additionally, since59Co is a mono-isotope,experimental data for59Co is ideal for the verification and development of nuclear reaction codes [24]. Furthermore, radioisotopes such as55Co and57Co that can be produced from the irradiation of protons on59Co are used for medical research. Proton data are also needed in the design and analysis of subcritical reactor systems such as the proposed MYRRHA reactor (Multi-purpose hYbrid Research Reactor for High-tech Applications), which would make use of spallation reactions in order to provide a source of external neutrons for its subcritical core [25].

2 Methods

2.1 Selection of experimental data

The first step in the nuclear data evaluation process is usually to carefully select experimental data since using all the experiments from the EXFOR database [26] without any selection normally leads to the computation of very large chi squares between model calculations and experiments.The large chi squares can be attributed partly to the presence of discrepant and outlier experiments as well as the presence of experiments with unreported or under-reported uncertainties. In this work, outliers were treated using a binary accept/reject approach. For example (as carried out also in Ref. [15]), experiments that were observed to be inconsistent with all or most of the data sets available for a particular channel and energy range were assigned a binary value of zero and therefore were not considered. In addition, experiments that deviate from the trend of the evaluations from the major nuclear data libraries (when available) were not considered. Similarly,experiments without reported uncertainties were penalized by assigning them a binary value of zero except in the cases where the considered experimental data set(s) under consideration were the only experiment(s) available in the energy range of interest. In this case, a 10% relative uncertainty is assumed for each data point of that particular experimental data set. Also, in a situation where these experimental data sets with unreported uncertainties have been considered and reported to be of reasonable quality in Ref. [27],a 10%relative uncertainty was assumed.In some cases, as carried out also in Ref. [27], experiments that were found to be close to the threshold energies and hence,usually difficult to measure, were not considered in our optimization procedure.

We note that the selection and rejection of experiments introduces bias into the evaluation process as is normally the case with all other evaluated nuclear data libraries.Ref. [4] however argues that, instead of rejecting discrepant and outlier experiments as carried out in this work,subjective weights which take into account the quality of each experimental data set, could instead, be assigned to each data set. In this way, ‘bad’ experiments would be assigned with smaller weights and hence contribute less to the optimization and therefore, no experimental information would be discarded. In Ref. [28], the use of Marginal Likelihood Optimization (MLO) for the automatic correction of the uncertainties of inconsistent experiments was proposed. Another approach as presented in Ref. [29] has been to identify Unrecognized Sources of Uncertainties(USU) in experiments and try to include them in evaluations. These approaches were however, not utilized in this work.

In this work,three experimental data types were utilized in the evaluation procedure:(1)reaction cross sections,(2)residual production cross sections, and (3) the elastic angular distributions. In the case of the reaction cross sections, the following eight reaction channels were considered: (p,non-el), (p,n), (p,3n), (p,4n), (p,2np)g,(p,2np)m, (p,γ), and (p,xn) cross sections. These channels were selected because(1)experimental data were available within the considered energy range for the considered cross sections of59Co and (2) because we desire a general purpose file which is optimized to many reaction channels with experimental data as much as possible.A total of 169 reaction crosssection experimental data points were used in the optimization. For the residual production cross sections, a total of 141 experimental data points were considered for the following cross sections:

·59Co(p,x)46Sc,

·59Co(p,x)48V,

·59Co(p,x)52Mn,

·59Co(p,x)55Fe,

·59Co(p,x)55Co,

·59Co(p,x)56Co,

·59Co(p,x)57Co,

·59Co(p,x)58Co,

·59Co(p,x)57Ni.

In the case of the elastic angular distributions, the angles were considered from 1° to 180° while the incident energies considered were from 5 to 40 MeV and a total of 185 experimental data points were considered.

2.2 Model calculations

Model calculations were performed using the TALYS version 1.9 [30] code. TALYS is a state-of-the-art nuclear reactions code used for the analysis of nuclear reactions for a number of incident particles. These particles include neutrons, protons, deuterons, tritons,3He- and α particles within the 1 keV to 200 MeV energy range [30].

In Table 1, similar to Ref. [20], the models considered in this work are listed. A total of 52 different physical models were randomly varied. A model as used here represents either a complete nuclear reaction model such as the Jeukenne—Lejeune—Mahaux optical model, or a submodel, and in some cases, components of a model or submodel. On the other hand, a model set or combination,represents a vector of these models or sub-models,coupled together in the TALYS code for nuclear reactioncalculations.For example,statepot is a flag used to invoke the optical model parameterization for each excited state in a Distorted Wave Born Approximation (DWBA) or coupled-channels calculation. As can be seen in Table 1, the TALYS code contains 4 pre-equilibrium models, 6 level density models,8 gamma-strength function models,4 mass models, and 4 Jeukenne—Lejeune—Mahaux (JLM) optical models, among others. Several of these models are linked together for nuclear reaction calculation with the outputs of some models used as input to other models. Even though all these models are available in TALYS, the default models have been used in proton evaluations for the proton sub-library of the TENDL library [20].

Table 1 List of selected TALYS models and sub-models considered for model variation

Since we assumed that all models were equally important a priori,our algorithm sampled each model type within its bounds.To achieved a non-informative prior as much as possible, each model type was sampled from a uniform distribution within its bounds. Models were then randomly drawn from each model distribution to create a total of about 200 model combinations. In the case of the level density (ld) model for example, there are six different models available in TALYS. Hence, these models were each assigned a unique ID and then sampled from model 1 to 6 in such a way that each ld model was equally likely to be selected. In addition, parameters to each model combination were also randomly generated to create multiply TALYS input files each with unique parameters,which were then run with the TALYS code to produce random cross-sectional curves as well as angular distributions.

Fig. 1 (Color online) 59Co(p,n) cross section computed with three different model combinations compared with cross sections computed with the default TALYS models (TENDL-2019), the JENDL/He-2007 and JENDL-4.0/HE libraries, as well as experimental data. The‘best’ file here is the optimal file selected from the parent generation taking into consideration, reaction and residual production cross sections as well as the elastic angular distributions. For each model combination A, B, and C, calculations were carried out with default and then perturbed model parameters

It should be noted that each model combination together with their unique parameter set gives different cross-sectional curves and angular distributions. In Fig. 1 for example,59Co(p,n) cross-sectional curves computed with three different model combinations are presented.Also,the calculated cross sections are compared with the default TALYS models (TENDL-2019) and the JENDL/He-2007 and JENDL-4.0/HE libraries as well as with experimental data. In the case of the models labelled (A) in the figure,the following models: ldmodel 6: Microscopic level densities (temperature dependent Hartree—Fock—Bogolyubov(HFB), Gogny force) from Hilaire’s combinatorial tables;preeqmode 4: Multi-step direct/compound model; strength 4: Hartree—Fock—Bogolyubov tables and massmodel 1:Mo¨ller table + other models, were used. For the model combination labelled (B), the following models were utilized: ldmodel 2: Back-shifted Fermi gas model; preeqmode 2: Exciton model:- Numerical transition rates with energy-dependent matrix element; strength 1: Kopecky-Uhl generalized Lorentzian, + other models. No mass model was invoked in this case of (B). In the case of models labelled (C), the cross-sectional curves were produced using ldmodel 3: Generalized superfluid model;preeqmode 2: Exciton model:- Numerical transition rates with energy-dependent matrix element; strength 4: Hartree—Fock—Bogolyubov(HFB)tables;massmodel 1:Mo¨ller table, +other models. The other models as stated here are default TALYS models that were included in the model calculations. For each model combination, two cross-sectional curves are shown: (1) with default parameters and the other with perturb parameters.These initial calculations give an idea of the shape and possible spread of the crosssectional curves for each model combination. It was observed in this work that the shape of the cross-sectional curves produced with each model combination was not affected with variation of the parameters and hence, a smaller number of parameters variations can be carried out around each model combination in the case of the initial or parent generation.It can be seen from the figure that model combination (B) gives a better fit to the available experimental data than model combinations (A) and (C). However, care must be taken as there is no guarantee that a model set which produces a good fit to experimental data for a particular channel would produce good fits for other channels.The‘best’file in Fig. 1 represents the optimal file selected from the parent generation (Gen. 0) taking into consideration both reaction and residual production cross sections as well as the elastic angular distributions. The parent generation here refers to the initial random nuclear data(ND)files produced from the variation of both models and their parameters and signifies the initial generation from which all subsequent generations were produced.Detailed description of the optimization procedure is presented in Sects. 2.3 and 2.4.

By randomly varying parameters of each model combination using the TALYS code package [30], a set of random nuclear data files in the Evaluated Nuclear Data File (ENDF) format were produced. Each TALYS input file contains a set of these models as presented in Table 1 as well as the parameters to these models(see Table 2).In a situation where a model type is not explicitly listed in the TALYS input file, a default TALYS model was used.

Similar to Table 1, a list of selected model parameters with their corresponding parameter widths (uncertainties)is presented in Table 2. A similar table is presented in Ref. [20]. The parameter uncertainties were obtained from the TENDL project [20, 30]. We note here that these parameter widths or uncertainties were obtained using default models in TALYS.We however think that this is a good enough starting point for our iBMC methodology.These parameter widths were used as prior uncertainties for the sampling of the parameters from a uniform distribution for each model combination used in this work. From the table, the parameter widths (uncertainties) are given as a fraction (%) of their absolute values except in the case of level density parameter a, and the gπand gνparameters of the pre-equilibrium model, where the uncertainties are given in terms of the mass number A.As can be seen from the table, the parameters have been grouped under the following model types: the optical model,pre-equilibrium,gamma-ray strength function and level density models. In the case of the optical model,the phenomenological optical model parameters are used for a potential of the Koning-Delaroche form [32] while the parameters for the semimicroscopic optical model are used for the Jeukenne—Lejeune—Mahaux (JLM) microscopic optical model potential [33]. Since the fission cross section was not considered in this work, fission models and their parameters are not presented in the table.

Table 2 List of selected model parameters with their parameter widths (uncertainties)

In the case of the pre-equilibrium model, gπand gνare the single-particle state densities, M2is the average squared matrix element used in the exciton model and Rγis the parameter for the pre-equilibrium γ-decay. Cstrip,Cbreakand Cknockare the stripping, break-up and knock-out contributions used to scale the complex-particle pre-equilibrium cross section per outgoing particle, respectively [31].Esurfis the effective well depth for surface effects in the exciton model. Rνν, Rπν, Rππ, and Rνπare, respectively, the neutron—neutron ratio,the proton-neutron ratio,the proton—proton ratio, and the neutron—proton ratio of the matrix element used in the two component exciton model. In the case of the level density model parameters, krot is the rotational enhancement factor of the level density model,σ2is the spin cutoff parameter which represents the width of the angular momentum distribution of the level density,a is the level-density parameter which is related to the density of single-particle states near the Fermi energy,and E0and T are the the back-shift energy and the temperature used in the constant temperature model,respectively.Rσis a global adjustable constant for the spin cutoff parameter.In the case of the gamma ray strength function, Γγis the average radiative capture width and σEℓ, EEℓand ΓEℓare the strength, energy and width of the giant resonance,respectively.Where Eℓ represents the electric(E)multipole type and ℓ the multipolarity [30]. These gamma-ray strength function parameters are used in the description of the gamma emission channel [30]. It should be noted here that not all the TALYS model parameters are listed in Table 2, a more complete list of all the model parameters can be found in Ref. [31]while the parameter uncertainties can be found in Refs. [4, 30]. As can be seen from the table,rather large parameter uncertainties were assigned to the krot, Cstrip, Cbreak and Cknock in order to take into account the shortcomings of the corresponding pre-equilibrium models [20]. As mentioned earlier, these parameters were varied simultaneously for each model combination to create multiple TALYS input files.

The incident proton energy grid for model calculations was selected taking into consideration the incident energies of the available experimental data as well as the availability of computational resources. It must be stated here that in order to observe the potential coverage of the parameter space for each model combination, two initial TALYS calculations are normally executed using two parameter vectors with extreme values, e.g., with: (1) the lower and (2) the upper bound values of each parameter.The lower and upper bounds corresponds to the minimum and maximum values of each parameter from the associated uniform prior parameter distributions. From these calculations, we are able to observe (visually) the trend and potential spread of the cross sections and the angular distributions of interest with respect to the scattered experimental data available. This was done because as mentioned earlier, the parameter widths as presented in Table 2 were obtained by comparing the cross-sectional curves produced with default TALYS model combination with varying parameters and hence, might not be applicable to other model combinations under consideration.Additionally, by observing the lower and upper bound curves, we are able to determine if any changes in the parameters within the uncertainties as given in Table 2,would significantly affect the spread of the considered cross sections.We note that since no parameter correlations were included in these initial calculations, this approach might not describe the entire coverage of the parameter space.This however is helpful in determining the potential uncertainty band for each cross section. Also, it must be stated here that we normally start with calculations with relatively small number of excitation energy bins of 20.The bin size is then increased to 60 for subsequent iterations in order to improve the accuracy of the TALYS results but at a higher computational cost.We note also that the total number of 200 model combinations used in this work does not cover the entire model space. We are however of the opinion that the number is adequate for demonstrating the applicability of the proposed method.

The 200 model combinations were each run with the TALYS code while varying all the model parameters to produce a large set of random ENDF nuclear data files.The random ENDF files produced were converted into x-y tables for comparison with experimental data. The reason for going through the TALYS → ENDF → x-y tables route instead of using the x-y tables directly produced by TALYS is because,during processing of TALYS results into the ENDF format, renormalizations are sometimes applied to the results using auxiliary codes such as the autonorm utility within the T6 code package [30]which is used to smoothen the results of TALYS at the incident energies where different model results are joined together [30]. These normalizations should normally not affect the results significantly, however, in order to enable a fair comparison between our evaluations and that of other nuclear data libraries which were only available in the ENDF format, the TALYS →ENDF →x-y route was used.

2.3 Bayesian calibration and selecting the winning model

The ultimate goal of a Bayesian calibration is to maximize the likelihood that model outputs are statistically consistent with experimental data [34].The first step in this work involves the pre-selection of models and their parameters, followed by the quantification of the uncertainties of model parameters and the determination of their distributions. As mentioned earlier, the parameter uncertainties were adopted from the TENDL library project. In this work, it was assumed that we have no prior information on the models as well as on their parameters and hence,the models and their parameters were both sampled from uniform distributions.This assumption is entirely not true since the model types used (see Table 1) were preselected using expert judgment and to some extent, model sensitivity analysis. The model sensitivity analysis involved holding constant all other models as the default TALYS models while changing the model of interest,oneat-a-time. The spread in the cross sections give an indication of the sensitivity of each model to the cross section of interest.For example,in Fig. 2,excitation functions for the59Co(p,3n) cross section computed with the four mass models implemented in the TALYS code is presented. No changes in the59Co(p,3n)cross section were observed after changing and running the different mass models one-at-atime for the energy range under consideration. This gives an indication that the mass models implemented in TALYS are not sensitive to the59Co(p,3n) cross section. The‘Best file (5th Gen.)’ in the figure represents the final evaluation obtained in this work while the TENDL-2019 represents the evaluation from the TENDL-2019 library.

Fig. 2 (Color online) 59Co(p,3n) cross section computed using the different mass models implemented in TALYS. All other models were maintained as the default TALYS models while changing each mass models one-at-a-time. The ‘Best file (5th Gen.)’ represents our evaluation.It can be observed that changing the mass models did not have any significant impact on the (p,3n) cross section

The pre-selection of models was carried out in order to limit the model space because of computational resource constraints. We do however understand that by using expert judgement to select a subset of the models available in the TALYS code system [30], we introduce some user bias into the initial model selection process. We however note here that since we are limited by the models available in TALYS in this case, selection bias cannot be entirely excluded from the process.A possible solution would have been to use all the models available in TALYS as well as additional models from other nuclear reaction codes such as EMPIRE [35]. This would increase the model space tremendously but would ultimately lead to a higher computation cost.A more detailed study on the use of Bayesian model selection and the Occam’s Razor in the selection of model combinations within a Total Monte Carlo framework is proposed and presented in Ref. [36].

Furthermore, it was observed in this study that some model combinations produced model outputs with nonsmooth curves which appear unphysical and therefore were excluded from subsequent model runs. For example, the59Co（p，γ） cross section computed with three different model combinations (A, B, and C) are compared with experimental data and the TENDL-2017 evaluation. Resonance-like structures which are difficult to explain from nuclear reaction theory were observed for59Co（p，γ）between about 4 and 10 MeV for model combination(A)as can be seen in Fig. 3, and therefore, this model combination was excluded from subsequent calculations. Note that model combinations (A), (B), and (C) are the same model combinations presented earlier in Fig. 1. As can be seen from Fig. 3, a relatively ‘bad’ model set such as model combination (A) can be difficult to identify by using only the χ2as the goodness of fit estimator since it can be observed that the cross-sectional curves produced by this model combination was able to reproduce quite favorably,the experimental data from Butler (1957). It can also be observed from the figure that the cross-sectional curves passes through some experimental data points from Drake(1973) which results in a relatively low χ2making it difficult to identify this model combination as a ‘bad’ model set.Because of this,visual inspection is sometimes needed to identify these ‘bad’ model sets. This should however be carried out on an isotope-by-isotope and channel-bychannel basis.

Fig. 3 (Color online) 59Co（p，γ） cross section computed with three different model combinations (A, B and C), are compared with cross sections computed with the default TALYS models (TENDL-2017),the JENDL/He-2007 and JENDL-4.0/HE libraries, as well as experimental data. The ‘best’ file is the file selected from the parent generation taking into consideration the reaction and residual production cross sections, and the elastic angular distributions. It can be observed that the curves from model combination (A) have non-smooth curves between 4 and 12 MeV which are difficult to explain from nuclear reaction theory

In the case of the input parameters to the models,all the parameters available within the TALYS code were varied.In this way, we were able to largely exclude parameter selection bias from our analyses. We however note that since only the TALYS code was used, we are constrained by the parameters available in TALYS. We also note that not all the model parameters are sensitive to the considered cross sections or the elastic angular distributions and therefore, these parameters could have been identified through a parameter sensitivity analyses and then excluded from the parameter variation process. This approach was however not carried out in this work.

Now,suppose that we have a set of J models,Mj→,where j=1，2，...，J, given a set of experimental data (σE→) with corresponding uncertainties (ΔσE→). Each model combination also consists of a vector of K model parameters, pk→,where k=1，2，...，K. As mentioned earlier, a model in this case refers to a vector of different models and submodels as presented in Table 1 while the parameter set denotes a vector of parameters to these models (see Table 2). As previously mentioned, we assume that all models are of equal importance a priori and therefore each model is characterized by a uniform prior distribution(P（Mj→，pk→）). As carried out also in Ref. [15], we assume that we have no prior knowledge on the model parameters and hence, the parameters pk→ were also drawn from a uniform distribution.Now,if L（σE→｜Mj→，pk→）is our likelihood function for model Mj→and parameter set pk→,the likelihood function can be given within the Bayesian Monte Carlo [4]and Unified Monte Carlo (UMCB-G and UMC-B) [8, 9]approaches as:

Equation 5 was computed assuming that there were no correlations between the different experimental data types considered.We note that this assumption is simplistic since in some cases, similar or the same instruments, methods,and authors were involved in the experiments and measurements of more than one experimental data type,which could introduce cross correlations between these experimental data types. For example, F. Ditroi was involved in the measurement and analysis of the reaction cross section,59Co(p,3n), between 16.0 and 69.8 MeV as well as in the measurement of the residual production cross section,59Co(p,x)56Co, between 15.0 and 69.8 MeV. However,these cross correlations are not readily available and therefore not used in this work.

Similarly, in the computation of the individual reduced chi squares in Eq. 6 such as the χ2k（xs）, the experimental data sets were assumed to be uncorrelated. To include experimental correlations, the generalized chi square as presented in Ref. [4] should have been used. However,experimental correlations are scarce especially with respect to proton induced reactions and when available,are usually incomplete.Therefore, the reduced chi square with respect to the reaction cross sections (χ2k（xs）) for example, was computed using Eq. 9 (similar expressions have been presented also in Refs. [4] and [17]):

In Refs. [15, 17], the reduced chi square presented in Eq. 9,was computed by averaging the chi square values for each channel over all the considered experimental data points. This approach, as stated also in Ref. [4], assigns equal weights (aside their uncertainties) to all the experimental data points which may lead to a situation where an experimental data set with a large number of measurements completely dominates the goodness of fit estimations.Also,channels with many different experimental data sets but fewer measurements would be assigned smaller weights compared to those with fewer experimental data sets but with many measurements.In an attempt to assign channels with many different experimental data sets with larger weights (aside their uncertainties) in line with what was carried out in Ref. [4], we averaged the chi square over each experimental data set by dividing by Nptas presented in Eq. 9. In this way, each experimental data set contributes equally to the goodness of fit estimation. Further,since the measurements from each data set are known to be highly correlated, by averaging over each experimental data set,we effectively combine the information from each experimental set into a single goodness of fit estimate.The correlations come about as a result of the fact that usually,the same equipment as well as methods(and authors)were used or involved in these measurements. It is also known that the addition of correlated experiments is not as effective in reducing the uncertainty in our calibration as the uncorrelated or independent experiments [37]. Experimental data set as used here refers to one or more measurements carried out at a specific energy or energy range,for a particular channel and isotope,with a unique EXFOR ID in the EXFOR database.

Statistical information of the posterior distribution in Bayesian estimations as presented in Eqs. 2 and 3, can normally be summarized by computing central tendency statistics [38],where the posterior mean is used as the best estimate(with its corresponding variance).However,given a large sample size and assuming that our prior was sampled from a uniform distribution,as stated in Ref. [39],the posterior probability density function (PDF) can be asymptotically approximated by a Gaussian PDF centered on the Maximum a Posteriori (MAP) estimate. Therefore,in this work, as used also in Bayesian Model Selection(BMS) [40],the best or winning model becomes the model(and parameter) set that maximizes the posterior probability which is also known as the Maximum a Posteriori(MAP) estimate (i.e., the mode of the posterior distribution), given as:

The LMAP and LMLE estimates were computed and compared for selected model parameters in the case of p+59Co and found to be the same(see Table 8).Therefore,from Eq. 11, the model combination (with its parameter set) which maximizes the likelihood function was considered as the winning model set and the file that makes the experimental data most probable.

2.4 Iterative Bayes procedure

The algorithm for the Iterative Bayesian procedure proposed in this work is presented in Table 3. The idea of the iterative procedure is to minimize the bias between our experimental observables and the corresponding model outputs in an iterative fashion. As can be seen from the table, we start with the selection of model combinations and their parameters(including parameter uncertainties and distributions)—see Table 1 for more information on the considered models. Next, we select the energy grid for the TALYS calculations.The energy grid was chosen such that there was a large number of matches in incident energy between the TALYS calculations and that of the corresponding experimental data. As mentioned earlier, we linearly interpolate in energy in the case of the reaction and residual production cross sections,and in angle,in the case of the elastic angular distributions,for the purpose of filling in the missing TALYS values.

Next, a set of random combinations of the models were generated from uniform distributions. In addition, the model parameters to each model combination were also sampled from uniform distributions to create a large set of TALYS input files.These input files were then run with theTALYS code system to produce a set of random nuclear data files in the ENDF format.These initial random nuclear data files constitute the parent generation (Gen. 0). The ENDF files produced were processed into x-y tables for the purpose of comparison with experimental data from the EXFOR database as well as with other nuclear data libraries, which were obtained in the ENDF format. The selection of experimental data for the considered channels has been presented earlier in Sect. 2.1.

Table 3 Iterative Bayesian Monte Carlo(iBMC)algorithm.L（σE→｜Mj→，pk→） is the likelihood function for each iteration (or generation), κ. σE→is our experimental data while Mj→is our model vector and pk→is a vector of model parameters for random file k. ESS is the Effective Sample Size given in Eq. 12. DA denotes angular distributions

Next, we select the ‘best’ model combination (with the parameter set) by identifying the random nuclear data file with the largest likelihood function value. Using this best file as our new central file or‘best’estimate,we re-sample around this file,however,this time only varying the model parameters of the selected model to produce another set of random nuclear data files referred to as the 1st generation(Gen.1).The idea here is that,once we are able to identify the‘best’model combination,we proceed with subsequent iterations as though the models selected were the true models. To proceed with the many different models for each iteration would imply that no model combination is good enough and hence, an average should instead, be taken over all or a selection of the models. This approach has been proposed and presented in a dedicated paper [22].

Next, is to update the model parameters and their uncertainties. However, before updating the parameter uncertainties, we first compute the Effective Sample Size(ESS). This was done in order to ensure that a sufficient number of effective samples are available for the computation of the posterior uncertainties and covariances. The effective sample size (ESS) is given as the squared sum of the file weights divided by the summed squares of these weights:The ESS is a useful metric for understanding the information value of each random nuclear data file and therefore gives an indication on how many random samples have significant impact on the posterior distribution. It has been noticed in this work that with an ESS ≤10%, very few random nuclear data files have significant impact on the posterior distribution and hence,as a rule of the thumb,we only update the parameter uncertainties for an ESS ≥10%.We then repeat our model parameter variation step(steps 3 through to 14 in Table 3) in an iterative fashion until we reach convergence.

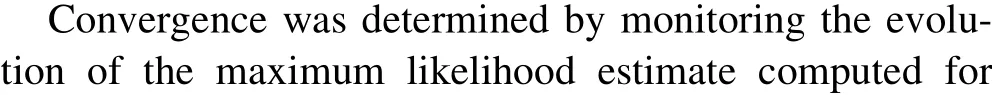
The iteration is said to have converged when the relative change in the maximum likelihood estimates(ΔLMLE)for the last two iterations is within a target global tolerance denoted by εG.In this work,we chose to set the value of εGto: εG≤0.05（5%）. It should be noted however that this value was chosen arbitrarily. Ideally, a smaller tolerance value (εG) is preferred however, small values of εGcan be difficult to achieve for a number of reasons:(1)because of the limitation of the models used, (2) the condition of Pareto optimality in multi-objective optimization, (3)computational resource constraint, and (4) when target accuracy is reached.In the case of(1),since the fit can only be improved with parameter variations within the limits of the selected models,we are constrained by the deficiencies of the winning model set. For example, if the winning model set is unable to reproduce the shape of experimental data for a particular channel, only varying the parameters would not be sufficient for improving the fits to experimental data. As mentioned earlier, the effects of model defects would then have to be taken into account in these cases.

With(2),a point worthy of note is that within the limits of our models in a multi-objective optimization procedure(as in this case), a point is reached in the iteration process,where further variation of the parameters is not able to improve the fits to the reaction cross sections for example,without making the fits to the residual production cross sections or elastic angular distributions worse-off. This condition is referred to as Pareto optimality [41]. This is because, multi-objective optimization problems as in our case, involves the simultaneous optimization of multiple competing objectives, which most often, leads to trade-off solutions largely known as Pareto-optimal solutions. A possible solution would be to assign subjective weights to each criteria or the chi square computed for each experimental data type as presented in Eq. 7 depending on the needs of the evaluation. For example, if the target of the evaluation is the production of radioisotopes, relatively larger weights could be assigned to the residual production cross sections in the computation of the global chi square.This would place more importance on the residual cross sections in the optimization procedure. Since the goal of this work was however to provide a general purpose evaluation which should compare reasonably well with experimental data for all or a large number of the cross sections, as well as the residual production cross section and angular distributions, equal weights were assigned to each individual experimental data type.As a general rule of the thumb,when no further improvements are possible with the global likelihood function, the iteration should be stopped since the Pareto optimum might have been reached.

For(3),the creation of random nuclear data files can be computationally expensive depending on the energy grid and the TALYS excitation bin size used. For example,more than 6000 random nuclear data files were produced and used in this work. This translated into several months of computational time.Therefore,the value of εGshould be chosen taken into consideration the accuracy gained as well as the computational resources available.In the case of(4),the value of εGcan be chosen with a particular objective or target accuracy in mind. For example, one underlying objective of this work has been to create an evaluation that globally outperforms and significantly improves the TENDL-2019 evaluation for the p+59Co. Hence, the iteration can be stopped after this objective is achieved. To check if the final results were robust to a change in εG, the adjusted results were compared with experimental data for different changes in εG: 15%, 10% and 5% and it was observed in the case of p+59Co and p+111Cd that the Pareto optimum was reached at about 5% for the reaction cross sections(see Table 5 for example).We note here that only static or energy-independent model parameters were used for the entire energy range under consideration,hence, this does not offer enough flexibility in the adjustment or fitting procedure. The use of energy-dependent parameters are proposed for future work.

Next, we return the final solution for Bayesian calibration, i.e., the final ‘best’ file. This file was then compared against available microscopic experimental data from the EXFOR database as well as with evaluations from other nuclear data libraries (if available). For testing and validation of the evaluation, we also compare our evaluation with experimental data from the channels that were not used in the optimization.This was done so as not to use the same experimental data for both adjustment and validation.Where available, the ‘best’ file should also be taken through integral validation where the evaluation is tested against a large set of integral benchmark experiments.These benchmarks are however, not readily available for proton induced reactions and therefore, not used in this work. Finally, we update also, the final parameter uncertainties (see Sect. 2.5).

2.5 Updating model parameter uncertainties

Once we are satisfied with the‘best’file,we move to the next step where we infer parameter uncertainties and covariance information to this file. We note here that in Bayesian inference, each parameter is described by a probability distribution instead of a point estimate. Therefore, by varying the model parameters around this file, we ensure that the prior parameter distribution is centered around the ‘best’ file. The covariance information associated with this file is then contained in the distribution of the random nuclear data files produced. Alternatively, as done in most nuclear data libraries, the covariance information associated with the evaluation can be stored in MF31-40(in ENDF terminology).

The flakes8 of snow covered her long fair hair, which fell in beautiful curls around her neck; but of that, of course, she never once now thought. From all the windows the candles were gleaming, and it smelt9 so deliciously of roast goose, for you know it was New Year s Eve; yes, of that she thought.

Under appropriate regularity conditions, the posterior can be approximated to a normal distribution with a mean and standard deviation [42]. Therefore, if we assume that the parameter posterior distribution is Gaussian,a weighted variance （varw（pι→）） for parameter (pι) can be computed as follows:

As mentioned earlier, given a large sample size and also that, the parameters are sampled from uniform distributions,the MLE is approximately equal or close to the mean values of each parameter. It is shown later in Table 8 that the mean values of the posterior parameter distributions were closed to the MLE estimates with respect to the optical model parameters as expected. Similarly, we can compute a weighted parameter covariance matrix between parameters pιand pτas follows:

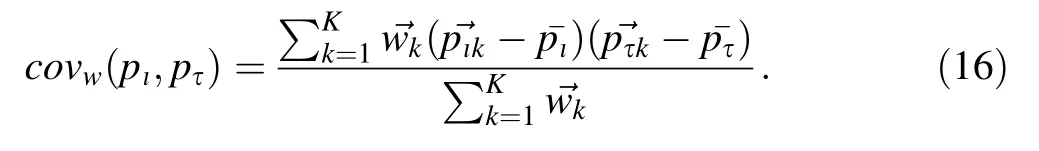
where ¯pιand ¯pτare the mean values of pιand pτparameters, respectively, pτkis the value of the parameter(pτ)in the random file k and covw（pι，pτ） is the weighted covariance matrix between parameters pιand pτ.

The use of the global likelihood function used in this work for updating the parameter uncertainties as presented in Eq. 4 raises a number of concerns:

1. Parameter sensitivities were not explicitly taken into account in the computation of the global reduced chi square as presented in Eq. 6. This is particularly important since each parameter would normally have different sensitivities to different cross sections and/or the angular distributions.This could lead to a situation where the weighted averaged parameters computed from the posterior distribution would not necessarily provide the best central values. In these cases, the parameter mean and the MLE values would be different. A possible solution would be to include parameter sensitivities as channel weights in the computation of χ2（xs）, χ2（rp） and χ2（DA）. In this way, if a particular channel is only sensitive to 2 or 3 parameters, this information would be included in the computation of the global reduced chi square. The inclusion of parameter sensitivities is however beyond the scope of this work.

2. The use of energy-independent parameters as used in this work does not give enough flexibility to the adjustment procedure. It should be noted here, as mentioned also in Ref. [4],that the predictive power of TALYS is energy dependent and therefore, the use of energy-dependent parameters in the computation of weights would give more flexibility to the adjustment procedure as parameters can be mapped to the weights in energy and/or in angle,thereby improving the ability to better constrain the model parameters to experimental data. An example on the use of energydependent parameters in the treatment of model defects for nuclear data evaluation is presented in Ref. [43].

3. Experimental correlations were not included in the optimization. Since some of the experimental errors are known to be correlated, these correlations should have been included by using the generalized chi square presented in Ref. [4]. However, since these correlations were not readily available, no correlations were used.

2.6 Updating the cross sections

Similar to Sect. 2.5, the weighted mean of the cross sections which corresponds to (or must be close to the values of the ‘best’ file) can be given as:

3 Results

In Table 4, the winning model combination, i.e., the models selected from the parent generation are compared with the corresponding default TALYS models for the p+59Co valid for the 1 to 100 MeV energy range. As mentioned earlier, the parameters to the selected models were subsequently varied to obtain the 1st generation random nuclear data files. It should be noted here that the proton sub-library of TENDL-2019 [20] were produced using default TALYS models and parameters. In the case where selected models were observed to be the same as the default models, these models were not listed in Table 4.Examples of these models include the widthmode(TALYS keyword used to invoke the models used for width fluctuation corrections in compound nucleus calculations),statepot (flag for specifying different optical model parameterization for each excited state in a Distorted Wave Born Approximation (DWBA) or coupled-channels calculation), gshell (flag to include the damping of shell effects with excitation energy in single-particle level densities), preeqsurface (flag to use surface corrections in the exciton model), and massmodel (flag used to invoke the models for nuclear masses). In the case of the mass model for example, there are four mass models available in TALYS however, massmodel 2: Goriely HFB-Skyrme table which is the default TALYS model was used and hence the mass model is not listed in Table 4. However, it was observed in this work that varying the mass models in TALYS did not have any significant impact on the considered cross sections and the elastic angular distributions.

In the case of the pre-equilibrium model, there are two versions of the exciton model available in TALYS:(1) the default two-component model in which the neutron or proton type of particles and holes are followed throughout the reaction and (2) the one-component model which does not distinguish between protons and neutrons. The exciton model has been proven to be a powerful tool for the analysis of continuum emission spectra and excitation functions for projectile energies above several MeV [45].From Table 4, it can be seen that the pre-equilibrium model 3 (denoted by the TALYS keyword preeqmode 3)was selected in place of the default exciton model (preeqmode 2). In the case of the default exciton model used in TALYS, the transition rates are expressed in terms of an effective squared matrix element while in the case of the selected PE model(preeqmode 3),instead of modeling the intranuclear transition rate by an average squared matrix element, the transition rate is related to the average imaginary optical model potential depth [31,45].Also,since the exciton models do not provide a spin distribution for the residual states after pre-equilibrium emission [45],TALYS gives the option to use either pre-equilibrium or compound nucleus spin distribution for the pre-equilibrium population of the residual nuclides.The default model implemented in TALYS is preeqspin 1 where the pre-equilibrium spin distribution is made equal to the relative spin-dependent population after compound nucleus emission [31]. However, preeqspin 2: the spin distribution from total level densities was selected in this work.

Similarly, in the case of level density (ld), the Backshifted Fermi gas model (ldmodel 2) was preferred to the default model (ldmodel 1: Constant Temperature + Fermi gas model).While the default ld and selected ld models are both phenomenological models, they defer in that in the case of the default model,the Constant Temperature Model(CTM) is used at low energies in combination with the Fermi gas model at high energies while in the case of the Back-shifted Fermi gas model, instead of using a constant temperature part, the model is expressed in terms of an effective excitation energy [20, 46]. Also, even thoughsome semi-microscopic optical (JLM) models were included in the model variations, the default phenomenological optical model potentials(OMP)as implemented in TALYS was selected. TALYS uses the local and global parameterizations of Koning and Delaroche [32,45]as the default optical model. In the case of the compound nucleus calculations, the default TALYS model for the width fluctuation correction (WFC) is the Moldauer expression,however, the Hofmann—Richert—Tepel—Weidenmu¨ller(HRTW) model was selected (i.e., TALYS keyword widthmode 2). Even though the HRTW model was selected, it was found in this work that using the HRTW model instead of the Moldauer model had no effect on proton induced reaction cross sections as expected. With the HRTW method, it is assumed that the main correlation effect between the incident and outgoing waves is in the elastic channel while with the Moldauer’s expression, a χ2law with ν degrees of freedom is assumed for the distribution for the partial widths (Γ), which can be calculated from a Porter-Thomas distribution [31, 47].

Table 4 List of the winning model combination obtained from the parent generation for p + 59Co compared with the default TALYS model

In relation to the strength function, the Gogny D1M Hartree—Fock—Bogoliubov (HFB) +quasiparticle randomphase approximation (QRPA) [48] (strength 8) was selected in place of the default Brink-Axel Lorentzian model [50, 51] (strength 2). It should be noted that for neutron induced reactions, the default model implemented in TALYS is the generalized Lorentzian form of Kopecky and Uhl(strength 1) [31,49].According to the Brink-Axel hypothesis, the photo-absorption cross section of the giant electric dipole resonance (GDR) is independent of the detailed structure of the initial state and assumes a standard Lorentzian form for the giant dipole resonance shape [49, 50]. However, even though the standard Lorentzian model accurately describes the GDR close to the resonance centroid for medium and heavy-mass nuclei [54],it often overestimates experimental gamma-ray strength functions at and below the neutron binding energy for dominant E1 radiation and therefore, other improvements such as the Generalized Lorentzian function (GLO)which includes the energy and temperature dependent width in the description of the GDR were developed [55, 56]. It is well known that the reliability of the gamma-ray strength predictions can be greatly improved through the use of microscopic and semi-microscopic models [57]. Therefore, by selecting the Gongny D1M HFB+QRPA model which is a microscopic model, it is expected that this would improve the gamma-ray strength function predictions and hence the description of the gamma emission channel. More information on Gogny-HFB+QRPA strength functions and its application to radiative nucleon capture cross section is presented in Ref. [56].

In Fig. 4, the global reduced χ2distribution as well as the reduced χ2distributions computed for the reaction and the residual production cross sections as well as the elastic angular distributions for p+59Co are presented. The χ2distributions in the plots represent the distribution from the 5th generation. Also in the same figure, the reduced chi square values computed for the ‘best’ file from the parent,1st, 2nd, 3rd, 4th, and the 5th generations, are compared with the values obtained for the TENDL-2019 evaluation using the same experimental data. The global reduced χ2distribution was obtained by taking the average over the different experimental data types considered.

From Fig. 4, it can be seen that our ‘best’ file from the parent generation did poorly compared with the evaluations from the other generations. This is expected since, first, a smaller number of excitation energy bins (20 bins) was used for TALYS calculations of the parent generation while a larger bin size of 60 was used for the other generations as well as for the TENDL-2019 evaluation. It has been observed that the accuracy of TALYS calculations increases with the number of excitation energy bins used.This however, comes at a higher computational cost. By using a smaller number of bins for the parent generation,we were able to run a relatively large number of different model combinations (200 model combinations in total).This however, did not have any significant impact on our model calculations since the same number of bins were used for all the models.From the figure,an improvement in the global reduced χ2can be observed from a high of 41.98 for the parent generation, to a low of 17.01 for our final evaluation (5th Gen.) as expected. Except for the parent generation, the evaluations from the other generations outperformed the TENDL evaluation:reduced χ2values of 41.98, 21.78, 19.51, 17.87, 17.40 and 17.01 were obtained for the parent, 1st, 2nd, 3rd, 4th and 5th generations compared with a reduced χ2value of 22.77 obtained for the TENDL-2019 evaluation. The reduced χ2value obtained for the reaction (χ2(xs) = 16.67) and residual production(χ2(rp) = 19.37) cross sections as well as for the elastic angular distributions (χ2(DA) = 15.00) for the 5th generation, performed better than the TENDL-2019 evaluation:χ2(xs) = 23.13, χ2(rp) = 20.77 and χ2(DA) = 24.94. Also,modest gains were made with regard to the 2nd and 3rd generations: a global average χ2value of 19.51 and 17.87 were obtained, respectively, compared with 21.78 for the 1st generation.This gives an indication that it is possible to improve our evaluations in an iterative fashion. A relative difference of 4.81% (which is less than the 5% target accuracy presented in Eq. 13) was obtained between the global MLE estimates of the 4th and 5th iterations implying that we have reached our targeted convergence value.

In Tables 5 and 6, the reduced chi squares values computed for the different channels used in the adjustments and for each generation, are compared with evaluations from the TENDL-2019 and JENDL-4.0/HE libraries for the reaction and residual production cross sections, respectively. Comparison was only made with the TENDL and the JENDL libraries since these were the only libraries with p+59Co evaluations.The Frankenstein files as presented in the tables were obtained by optimizing model calculations to experimental data for each individual cross section (or the elastic angular distributions), one at a time.

Fig. 4 (Color online) A distribution of the reduced χ2 obtained from the 5th generation showing values obtained for the ‘best’ files from the parent, 1st, 2nd, 3rd, 4th, and 5th generations as well as with the evaluation from TENDL-2019. xs denotes reaction cross sections,rp—residual production cross sections and DA—angular distributions. The global reduced χ2 was computed by combining the individual reduced χ2 values obtained from the different experimental data types

Table 5 Comparison of the reduced chi square values between‘best’files from different the generations and the evaluations from the TENDL-2019 and JENDL-4.0/HE libraries for p+59Co between 1-100 MeV, in the case of reaction cross sections

Table 6 Comparison of the reduced chi square values between the‘best’files from different generations and the evaluations from the TENDL-2019 and JENDL-4.0/HE libraries for p+59Co between 1 and 100 MeV in the case of residual cross sections

From Table 5,it can be seen from the large reduced chi squares obtained for the (p,γ) channel for all the generations that it was difficult for the models in TALYS to reproduce the experimental data for the (p,γ) cross section.In the case of the JENDL-4.0/HE library,a very large reduced chi square value of 1367.91 was obtained for the(p,γ) cross section signifying that the JENDL-4.0/HE evaluation was completely off the experimental data for the(p,γ) channel. This can be confirmed visually from Fig. 5 where the JENDL-4.0/HE evaluation for example, was observed to have significantly under-predicted all the data from Drake (1973) but reproduces the data from Butler(1957) relatively well. This accounts for the large reduced chi square obtained for the (p,γ) cross-sectional evaluation from the JENDL-4.0/HE library. A relatively smaller reduced chi square value of 40.33 was however obtained for the TENDL-2019 evaluation compared with a value of 53.93 from this work(Best file(5th Gen.)).This value was however, reduced to 36.83 for the Frankenstein file. It should be noted here that the Frankenstein file is however,constrained by the model combination used.The relatively large reduced chi square values obtained for the(p,γ)cross section in the case of the evaluations from this work is largely due to the inability of our models to reproduce the two experimental data sets available. We observed in this work that model combinations that were able to fit the data from Butler (1957) where unable to fit data from Drake(1973) and vice versa. Hence, only trade-off solutions could be obtained. We however note here that it is impossible to cover the entire model and parameter space and hence, there would always be a possibility that better solutions may exist in some hidden region of the model and/or parameter space necessitating for the use of more efficient sampling approaches than the brute force approach used in this work. It is instructive to note that even though the use of surrogate models could greatly reduce the computational cost burden,we think that the use of surrogate models would further introduce some simplifications and assumptions into our model calculations since they are simplified approximations of more complex models such as the models used in nuclear data evaluations. For both experiments (i.e., Drake (1973) and Butler(1957)), no experimental uncertainties were reported,hence, a 10% relative uncertainty was assumed for each data point since these were the only experimental data sets available within the considered energy range. Also, no cross-sectional data were available for the(p,non),(p,np)g,and (p,np)m channels in the JENDL-4.0/HE library and therefore, the average reduced chi square presented in Table 5 for the JENDL-4.0/HE evaluation is an average over the (p,n), (p,3n), (p,4n), (p,γ) and the (p,xn) reaction channels.

In the case of the residual production cross sections presented in Table 6, it can be seen that the59Co(p,x)48V cross section benefited greatly from the iterative procedure;a large reduced chi square value of 172 for the parent generation was significantly decreased to a value of 49.28(Gen.1),39.81(Gen.2),37.28(Gen.3),35.38(Gen.4)and 14.73 (Gen.5). It was however observed that the JENDL-4.0/HE evaluations outperformed the evaluations from this work and that from the TENDL-2019 library; reduced chi square values of 13.42 and 60.02 were obtained for the JENDL-4.0/HE and TENDL-2019,respectively.As can be seen in Fig. 7,the JENDL-4.0/HE evaluation appears to be reproducing the experimental data from Michel (1985)while the evaluation from this work appears to be reproducing experimental data from Michel (1997). In fact, the JENDL-4.0/HE library outperformed our evaluations except in the case of the59Co(p,x)57Ni, where our evaluation(Gen.5)was observed to be in a better agreement with experimental data. As mentioned previously, one disadvantage of a multi-objective optimization procedure is that it gives the best trade-off solutions, hence a situation can occur (as in this case), where even though our evaluation performs better globally, it performed badly when compared locally with experimental data.

In Table 7, a comparison of the reduced chi square values obtained for the different generations and that of the TENDL-2019 library for p+59Co between 1-100 MeV are presented for the elastic angular distributions. No evaluation was available in the JENDL-4.0/He and JENDL/He-2007 libraries for p+59Co elastic angular distributions and therefore, were not presented. Similar to Tables 5 and 6,the Frankenstein file in the table denotes the file obtained by optimizing model calculations to only the elasticangular distributions. Also, it should be noted that for the parent generation(Gen. 0),the following incident energies were not computed with TALYS: 5.25, 6.50, 7.00, 7.50,30.30 and 40.00 MeV, and therefore, no results were reported for these energies in the case of parent generation in Table 7. This was done in order to speed up the calculational time for the parent generation. It should be noted however that, this did not have significant impact on the optimization since the spread of the elastic angular distributions due to model variations was observed to be relatively small (see Fig. 9). Furthermore, it can be seen from the table that the evaluations from the 5th generation is an improvement on the Gen.0,1 and 2.The reduced chi square value however increased to 17.14 for Gen.4 before reducing again to 15.00 for the 5th Gen. It was also observed that our evaluation significantly outperformed the TENDL-2019 evaluation where a reduced χ2= 22.95 was obtained.In addition,it can be observed from Tables 5 and 7 that by optimizing model calculations to single channels or only the elastic angular distributions, relatively smalleraveraged reduced chi square values can be obtained as can be seen with the Frankenstein files.

Fig. 5 (Color online) Excitation functions against incident proton energies for the following reaction cross sections: (p,non-el), (p,n),(p,3n),(p,γ),(p,4n),and(p,np)m.The evaluation from this work(i.e.,Best file (5th Gen.)) is compared with the evaluations from TENDL-2019, and the JENDL/He-2007 and JENDL-4.0/HE libraries, and experimental data from EXFOR. The curves in violet represent random cross sections from the 5th generation

Table 7 (Color online) Comparison of the reduced chi square values between the ‘best’ files from different generations and the TENDL-2019 evaluation for p+59Co between 1 and 100 MeV in the case of the elastic angular distributions

In Fig. 5, excitation functions for the (p,non-el), (p,n),(p,3n) and (p,γ), (p,4n) and (p,np)m cross sections of59Co are compared with the evaluations from the TENDL-2019 library. Also, where available, comparisons are made with evaluations from JENDL-4.0/HE as well as with evaluations from the older JENDL/He-2007 library.It can be seen from the figure that our evaluation performed slightly better than the TENDL-2019 library for the(p,non-el)cross section over the entire energy region. It can be seen that both evaluations slightly over predicted the data from Mccamis (1986) between about 35 and 50 MeV. Even though the TENDL-2019 evaluation slightly over predicted the data from Kirkby (1966) at 98.5 MeV, our evaluation was within its experimental uncertainties which resulted in a reduced chi square value of 0.041292. For the (p,3n)cross section,the TENDL-2019 evaluation under predicted the experimental cross sections from about 45 to 100 MeV.The evaluation from this work was however observed to be in good agreement with experimental data from Sharp(1956) and Ditroi (2013) and also, data from Sharp (1956)and Michel (1997) from about 60 to 100 MeV as well as with Johnson (1984) between about 35 and 42 MeV. In general, in the case of the (p,γ) channel, it was observed that the models in TALYS had difficulty reproducing the two experimental data available altogether. Hence, it can observed that the TENDL-2019 for example under predicted most of the data from Butler (1957). Also, the JENDL-4.0/HE evaluation severely under predicted the data from Drake(1973)but fits relatively well with most of the experiments from Butler (1957). Our (p,γ) evaluation appears to be a trade-off solution for the two experimental data sets available. In the case of the (p,4n) channel, our evaluation compares favorably with experiments from Church(1969)and Michel(1979)between 35 and about 50 MeV and compares well with Michel (1997) and Ditroi(2013) between 60 and 100 MeV. The TENDL-2019 evaluation appears to fit the experimental data from Sharp(1956) between 60 and 100 MeV but was unable to reproduce experiments in the threshold and lower energies.The JENDL-4.0/HE evaluation, similar to this work,described data from Michel (1979) favorably but under predicted the data from the experiments in the high energy region between about 55 to 100 MeV. In the case of the(p,np)m cross section, both TENDL-2019 and the evaluation from this work were unable to reproduce experiments at the threshold energies to about 22 MeV. Our evaluation however reproduced favorably the experimental data from about 22 to 30 MeV.

With respect to the(p,n)channel,it can be seen that our evaluation describes the experimental data in the lower energy region as well as data from Chodil (1967) reasonably well. It was however observed that the JENDL/He-2007 evaluation for the (p,n) channel outperformed both our evaluation and that from the TENDL-2019 and JENDL-4.0/HE libraries especially between about 5 - 12 MeV. Interestingly, the evaluation from JENDL-4.0/HE appears to be worse-off compared with the JENDL/He-2007 library which is an older library. One observation made in this work is that it appears more effort was put into improving the residual production cross sections of59Co in the JENDL-4.0/HE library than the reaction cross sections.

In Fig. 6,cross sections against incident proton energies computed for the following residual cross sections:59Co(p,x)56Co,59Co(p,x)55Co,59Co(p,x)57Ni and59Co(p,x)51Cr are compared with the evaluations from the TENDL-2019, the JENDL/He-2007 and JENDL-4.0/HE libraries. Similarly, in Fig. 7, the following residual cross sections:59Co(p,x)51Mn,59Co(p,x)54Mn,59Co(p,x)48V and59Co(p,x)46Sc, are presented. From the Fig. 6, it can be seen that our evaluation and that from the JENDL-4.0/HE and the JENDL/He-2007 libraries are in good agreement with experimental data with reference to the59Co(p,x)57Ni cross section. However, the TENDL-2019 evaluation slightly under predicts all the data in the entire energy region shown. In the case of the59Co(p,x)56Co cross section, our evaluation is in good agreement with data in the threshold energies but under predicted experimental data in the lower energy range between about 30 to 70 MeV.Similarly, the TENDL-2019 and JENDL/He-2007 evaluations had difficulty in reproducing the experimental data especially at the lower energies. However, the JENDL/He-2007 and the TENDL-2019 evaluations are in good agreement with experimental data from about 50 to 100 MeV. The JENDL-4.0/HE evaluation was however in good agreement with experimental data from the threshold to about 48 MeV but similar to our evaluation, under predicted experimental data from about 50 to 100 meV for the59Co(p,x)56Co cross section.

In the case of the59Co(p,x)55Co, the TENDL-2019 and JENDL-4.0/HE evaluation compares favorably with the experimental data than our evaluation and that of the JENDL/He-2007 library. This accounted for the relatively smaller reduced chi squared obtained for TENDL-2019(7.24) and JENDL-4.0/HE (4.10) compared with 22.75 for our evaluation in Table 6. Similarly, in the case of59Co(p,x)51Cr, it can be observed that the JENDL-4.0/HE evaluation reproduces the shape of the cross section quite well except in the very high energy region between about 85 and 100 MeV where it under predicted the cross section by large margins. Our evaluation and the JENDL/He-2007 evaluation however, compared favorably with experimental data at the threshold energies. It was observed that the JENDL/He-2007 library over predicted the59Co(p,x)55Co cross sections with large margins from about 55 to 100 MeV and also data from the threshold to about 55 MeV.The JENDL-4.0/HE evaluation of59Co(p,x)55Co can be said to be a major improvement in the JENDL/He-2007 evaluation.

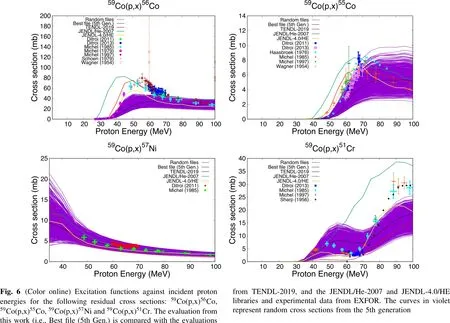
Fig. 6 (Color online) Excitation functions against incident proton energies for the following residual cross sections: 59Co(p,x)56Co,59Co(p,x)55Co, 59Co(p,x)57Ni and 59Co(p,x)51Cr.The evaluation from this work (i.e., Best file (5th Gen.) is compared with the evaluations from TENDL-2019, and the JENDL/He-2007 and JENDL-4.0/HE libraries and experimental data from EXFOR. The curves in violet represent random cross sections from the 5th generation

Fig. 7 (Color online) Excitation functions against incident proton energies for the following residual cross sections: 59Co(p,x)51Mn,59Co(p,x)54Mn, 59Co(p,x)48V and 59Co(p,x)46Sc.The evaluation from this work is compared with the evaluations from TENDL-2019,JENDL/He-2007 and JENDL-4.0/HE libraries,and experimental data from EXFOR. The curves in violet represent random cross sections from the 5th generation

For the59Co(p,x)51Mn,59Co(p,x)54Mn,59Co(p,x)48V and59Co(p,x)46Sc cross sections presented in Fig. 7, our evaluation was seen to be in good agreement with experimental data and in fact, outperformed the TENDL-2019 evaluations for all the channels presented. In the case of59Co(p,x)51Mn for example, our evaluation satisfactorily fits experimental data from Sharp(1956)and is observed to be within the experimental uncertainty of the data from Wagner (1954). Since no experimental uncertainties were recorded for Sharp(1956),a 10%uncertainty was assumed.For59Co(p,x)48V,our evaluation is in good agreement with experimental data from Titarenko (1996) as well as with data from Michel(1985),from threshold to about 90 MeV.The JENDL/He-2007 evaluation appears to be fitting data from Sharp (1956) which came with no corresponding experimental uncertainties.On the other hand,the TENDL-2019 evaluation is observed to have under predicted all the experimental data from about 75 to 100 MeV but was seen to be in agreement with data at the threshold energies. In addition, the JENDL-4.0/HE evaluation fits satisfactorily the experiments from Michel (1985) from threshold to about 95 MeV but under predicts data at 98.2 MeV. With reference to the59Co(p,x)54Mn cross section, our evaluation as well as the TENDL-2019 evaluation had difficulty in reproducing experiments at the threshold energies.However, our evaluation described the data from Michel(1995)satisfactorily between about 30 and 35 MeV as well as data between 50 and 70 MeV but was unable to fit the experimental data from about 70 to 100 MeV for the59Co(p,x)54Mn cross section. The JENDL/He-2007 evaluation on the other hand, fitted well experiments from Johnson (1984) between about 28 and 40 MeV but over estimated data from 45 to 85 MeV. In the case of the59Co(p,x)46Sc cross section, it can be seen that our evaluation and that of the JENDL-4.0/HE library outperforms the TENDL-2019 evaluation over the entire energy region.Excitation functions against incident proton energies for the following residual cross sections:59Co(p,x)g58Co,59Co(p,x)m58Co,59Co(p,x)58Co and59Co(p,x)57Co are presented and compared with the TENDL-2019 evaluation as wll as experimental data in Fig. 8. It can be observed that our evaluations over predicted the59Co(p,x)58Co and the59Co(p,x)57Co cross sections from 45 to 100 MeV. On the other hand, the evaluations from this work as well as from the TENDL-2019 library compares favorably with experimental data for the59Co(p,x)g58Co and59Co(p,x)m58Co cross sections. For the purpose of testing our evaluations, we used channels such as the59Co(p,x)51Mn,59Co(p,x)54Mn,59Co(p,x)51Cr,59Co(p,x)g58Co and59Co(p,x)m58Co that were not used in the optimization procedure. These cross sections are produced with each TALYS calculation. This was done in order that the same channels used for adjustment were not used for testing and validation purposes.It can be observed from Figs. 6, 7 and 8 that the cross sections from this evaluation compared relatively well compared with experimental data as well as the TENDL-2019 evaluation.

Fig. 8 (Color online) Excitation functions against incident proton energies for the following residual cross sections: 59Co(p,x)g58Co,59Co(p,x)m58Co, 59Co(p,x)58Co and 59Co(p,x)57Co. The evaluation from this work is compared with the evaluations from TENDL-2019 library and experimental data from EXFOR. The curves in violet represent random cross sections from the 5th generation

In Fig. 9, cross section against angles (°) for selected incident energies: (a) 11.0 MeV, (b) 7 MeV, (c) 7.4 MeV,(d) 6.05 MeV, (e) 9.67 MeV and (f) 30.3 MeV, are presented for the elastic angular distributions of p+59Co from this work and compared with the evaluation from the TENDL-2019 library.No elastic angular distributions were found in the TENDL-2019 evaluation of p+59Co therefore,the TENDL-2019 elastic angular distributions presented in the figure were obtained by running the TALYS code with the model and parameter sets used to create the TENDL-2019 p+59Co evaluation. In order to enable a good match between our evaluations and experimental data, the experimental incident energies at which the elastic angular distribution were measured were given to the TALYS code as input. From Fig. 9, it can be observed that our evaluations fits satisfactorily the experimental data for all angles except at high angles where some deviations were observed. For example, it can be observed from the figure that the evaluation from this work under predicted the experimental data from about 150°to 180°for the incident energies En=7.4,9.67,11.0,MeV.It can also be observed that the evaluation from this work outperformed the TENDL-2019 evaluation for all the incident energies presented except in the case of En= 9.67 MeV where it is observed that the TENDL-2019 evaluation compared more favorably with experiments from about 140° to 180°.

Fig. 9 (Color online) Cross sections against angles (°) for selected incident energies:a.11.0 MeV,b.7 MeV,c.7.4 MeV,d.6.05 MeV,e. 9.67 MeV and f. 30.3 MeV for elastic angular distributions of p+59Co. The evaluation from this work (‘Best’ file (5th Gen.)) is compared with the TENDL-2019 evaluation.The TENDL evaluation was obtained by rerunning the TALYS code with the same model and parameter set used to create the TENDL-2019 evaluation.The plots in violet represent random cross sections from the 5th generation

3.1 Final parameter uncertainties

To show the convergence of the posterior parameter distributions of the 5th generation, we present a plot example of the convergence of the posterior mean and standard deviation for the vso2adjust (vpso2) parameter in Fig. 10. It can be seen from the figure that even though over a thousand samples were produced, the mean and the standard deviation converges well after about 600 runs or samples.The fluctuations observed after 600 samples were found to be below 1%.Similar plots(not shown)have been produced for the other model parameters and it was observed that a large number of the parameters converged after about 800 samples. For uncertainty propagation to applications purposes, within the Total Monte Carlo approach, it has been observed earlier that convergence could be reached after 300 samples [60].

Fig.10 (Color online)Plot example showing the convergence of the posterior mean and the standard deviation of the vso2adjust optical model parameter distribution (for p + 59Co). The parameter distribution used here was obtained by re-sampling the parameters around the ‘best’ file values obtained from the 5th generation

Fig. 11 (Color online) Distribution of global file weights for p +59Co computed using Eq. 4. The weights have been normalized with the maximum weight in order to relate them to 1

In Fig. 11, a distribution of the file weights computed for p+59Co using Eq. 4,is presented.As expected,a large number of files were assigned with low or insignificant file weights and therefore contributed less to the final (or posterior) uncertainties. This is consistent with earlier results presented with respect to neutron induced reactions in Refs. [10, 15]. The low and insignificant weights obtained could be attributed to the following: (1) the presence of outlier experiments as well as experiments with unreported or under-reported uncertainties, (2) sampling from a region of the parameter space where the likelihood is probably low, (3) the difficulty in optimizing our fits simultaneously to three different experimental data types considered, (4) the presence of model defects, and (5) not considering experimental correlations in the computation of the χ2.In the case of(1),data considered as outlier were assigned with a binary value of zero and therefore not considered in the optimization. Even though outlier experiments were discarded, it was still observed that our models had difficulty in reproducing experimental data especially at the threshold energies. It is observed in Ref. [4] that, the nuclear model calculations can easily be several factors off experimental data at the threshold energies as well as at the high-energy tail of the excitation function.Our solution here has been to exclude a few data points at the threshold regions for cross sections. Furthermore, instead of rejecting outlier experiments, it is proposed that approaches for the automatic correction of the uncertainties of inconsistent experiments and the identification of Unrecognized Sources of Uncertainties (USU) in experiments proposed in Refs. [28] and [29], respectively,be incorporated into the iBMC methodology in future work.

To address(2),an accept/reject method could be used to reject samples with insignificant file weights as carried out in Ref. [15].This approach could however introduce some bias depending on the cutoff parameter. Therefore, instead of rejecting samples, we instead, compute an Effective Sample Size (ESS) using Eq. 12 in order to ensure that a sufficient number of effective samples were available for the computation of the final posterior moments.In the case of (3), it was observed that optimizing our model calculations to three experimental data types simultaneously can be difficult. A solution would be to optimize each experimental data type or cross section individually and then combine them into an evaluation. This would however,lead to inconsistent evaluations as the sum rules must be obeyed. With respect to (5), experimental correlations and covariances are often not readily available and therefore were not considered in this work. The inclusion of these correlations is however recommended for future work.

Table 8 presents a comparison between the posterior mean and the Maximum Likelihood Estimate (MLE) values for a selected number of model parameters in the case of the 5th generation (p +59Co). The corresponding updated uncertainties obtained from each posterior parameter distribution are also presented.The mean values were obtained by taking the weighted average of the posterior distribution of each parameter using the computed file weights while the MLE values are the parameter values of the TALYS input file with the maximum likelihood estimate (i.e., the final ‘best’ file). It was observed in this work that the MAP estimate was the same as the MLE values as expected and therefore, not included in Table 8.

Similar to the prior parameter uncertainty values given in Table 2, the updated (posterior) uncertainties are given as a fraction (%) of the posterior mean values. It can be seen from the table that the MLE and the posterior mean values are close for most of the optical model parameters presented as expected—a relative difference of less than 1%was obtained for most of the optical parameters.This is not surprising, as mentioned earlier, under appropriate regularity conditions, the posterior distribution should be centered at or close to the MLE values. However, large relative change between the MLE and the mean values of more than 10% were recorded for example, in the case of the spin cutoff parameter (e.g., σ2（56Fe）) of the level density model and the single-particle state densities(gπ（56Fe）). For these parameters, it was observed that the prior parameter distributions were not flat but were rather skewed towards the right. This could be attributed to the inability of our algorithm to sample the entire space of these parameters and would therefore require a larger number of samples.

From the table, a relatively significant reduction in the prior uncertainty is observed for a number of parameters.For example, a prior uncertainty of 5% was reduced to 3.5% for the avdadjust parameter and a 20% prior uncertainty was reduced to 8.2% and 7.4% for the wso1adjust and wso2adjust parameters, respectively. Also, a prior uncertainty of 10% and 2% were reduced to 4.5% and 1.3%, respectively, for the rcadjust and the rvadjust parameters. Small or negligible reductions were however observed for parameters such as v1adjust: (from 2 to 1.8%),and in the case of v2adjust and v3adjust parameters,from 3 to 2.7%. For the d1adjust, d2adjust and d3adjust parameters,the prior uncertainties were reduced from 10%for each parameter, to 7.6%, 7.7% and 8.4%, respectively.A large reduction in posterior spread (uncertainties) gives an indication that the parameter under consideration has alarge sensitivity to the channels used in computing the global likelihood function. On the other hand, small or no reduction in the posterior uncertainty implies that the file weights do not have impact on the posterior parameter distribution of interest, signifying no sensitivity of the parameter under consideration to the channels used in the computation of the weights. This is because, by using a uniform or relatively flat priors (as was in this case), the posterior distribution is determined solely (or almost) by the experimental data through the likelihood function.

Table 8 Comparison between the posterior mean (with corresponding updated parameter uncertainties) and the MLE for selected model parameters using file weights computed with files from the 5th generation

Fig.12 (Color online)Prior and posterior parameter distributions for selected optical model parameters: avadjust (apV), avdadjust (apD),v1adjust (vp1), rvadjust (rpV) in the case of the p + 59Co (Gen. 5). An

Effective Sample Size (ESS) of 110 (representing 10.8% of the total sample size) was obtained

In Fig. 12, prior and posterior distributions for selected optical model parameters in the case of the 5th generation: avadjust (apV), avdadjust (apD), v1adjust (vp1), w1adjust (wp1)are presented. As can be seen from the figure, the prior samples were drawn from uniform parameter distributions.The posterior distributions describes the updated information for the considered parameters after experimental data were taken into account. In general, it can be seen that the priors are relatively flat as expected. However, the posterior distribution peaks sharply at the mean value which incidentally is very close to the MLE and the MAP values as expected.The posterior(or updated)uncertainties for the parameters in Fig. 12 are as follows: apV—1.8% (reduced from 2%), apD—3.5% (reduced from 4%), vp1—1.8% (reduced from 2%), rpV—1.3% (reduced from 2%). An Effective Sample Size (ESS) of 110 which represents 10.8%of the total sample size,was obtained.Our inability to significantly reduce the posterior uncertainties for some of the parameters can be attributed to the insensitivity of these parameters to the cross sections and the elastic angular distributions used in computing the file weights.

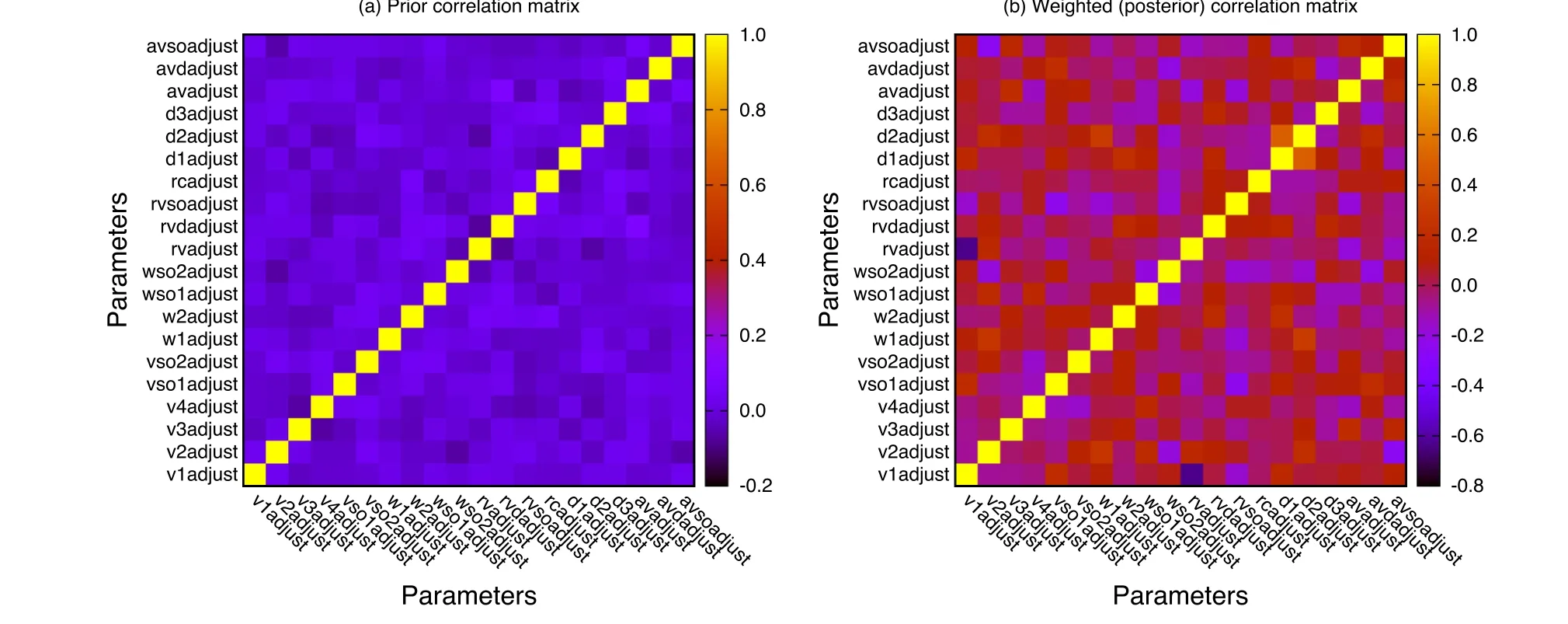
Fig.13 (Color online)Prior and posterior(weighted)correlation matrices for a selected number of optical model parameters for p+ 59Co(Gen.5)

Fig. 14 (Color online) Evaluated posterior correlation matrix for selected proton induced cross sections of p + 59Co (Gen. 5). The incident energy used corresponds to the incident energies of the experimental data used in the computation of the file weights

As a natural consequence of the Monte Carlo method used, correlations and other statistical information such as mean and variances can be extracted from both the prior and posterior distributions. In Fig. 13, prior and posterior(weighted) correlation matrices for a selected number of optical model parameters are presented. The correlation matrices presented are symmetric and give a measure of the strength of the linear dependence between two parameters and vary from -1 (perfect negative correlation) to +1(perfect positive correlation). It can be seen from the figure that the prior correlation values are generally relatively low.This is expected since the parameters were sampled in an uncorrelated manner. Additional correlations were then introduced through the use of the same experimental data used in the computation of the file weights as can be seen in the weighted(posterior)correlation matrix in Fig. 13.A negative correlation was observed between the rvadjust(rpV) and v1adjust (vp1) parameters for example. This is expected as there is a well-known inverse relationship between the rpVand vp1parameters which can be given as follows:vp1*rpV=constant [61].It must also be noted that most of the optical models showed similar behavior as can be seen in Fig. 13. Similar negative correlations were also observed in Ref. [61]. We note here that these parameter correlations were however, automatically taken into account in the simultaneous variations of the model parameters. Similarly, energy—energy correlations for each cross section can be obtained. As proof of principle,evaluated posterior correlation matrices for selected proton induced reaction cross sections ((p,nonel), (p,n), Co(p,γ)and (p,4n)) of p +59Co are presented in Fig. 14. Similar matrices (not shown) were obtained for the residual production cross sections and the elastic angular distributions.These matrices were obtained by combining the global file weights with the cross sections. The high correlations as seen in the figure can be attributed largely to the energy—energy correlations that come from the use of the same theoretical models in the production of the random cross sections. A similar observation was made in Ref. [60].Additional correlations come from the use of the same experimental data in the computation of the file weights.This however, has less impact since the correlations were introduced through the global likelihood function which also took into account, experimental residual cross-section data as well as the elastic angular distributions. These weighted correlations and covariance information can be used for uncertainty propagation to applications.It must be stated here that even though these parameter correlations and covariances are available,the final cross sections were produced from the direct variation of model parameters and not from perturbing the cross sections.

4 Conclusion

In this work, we explored the use of an Iterative Bayesian Monte Carlo (iBMC) procedure for the evaluation of nuclear data in the fast energy region. The goal of the iterative procedure has been to minimize the difference between selected experimental observables and the corresponding nuclear reaction model outputs in an iterative fashion. This was done by exploring both the model and parameter space in order to identify the ‘best’ model combination and corresponding parameter set, that make our experimental data most probable within a Bayesian Monte Carlo framework. The associated uncertainties of the final evaluation were obtained by re-sampling model parameters around the final‘best’file.The proposed iBMC method has been applied to the evaluation of proton induced reactions on59Co between 1 and 100 MeV energy region. The study showed that there is a potential for the improvement of nuclear data evaluations within the limit of the available models, through an iterative process. Since the selected models were still observed to be deficient in their ability to reproduce the experimental data available,we propose the integration and inclusion of model defects into the iBMC methodology. Furthermore, since it was difficult to cover the entire model and parameter space,it is further recommended that more efficient sampling methods be explored in future work.

AcknowledgementsThe authors would like to thank Georg Schnabel from the IAEA and H. Sjo¨strand from Uppsala University for interesting discussions on this topic,as well as to the anonymous referees for many helpful comments.

Author ContributionsAll authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Erwin Alhassan, Dimitri Rochman, Alexander Vasiliev,Mathieu Hursin,Arjan J.Koning and Hakim Ferroukhi.The first draft of the manuscript was written by Erwin Alhassan and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

FundingOpen Access funding provided by Lib4RI—Library for the Research Institutes within the ETH Domain: Eawag, Empa, PSI &WSL. This work was done with funding from the Paul Scherrer Institute through the NES/GFA-ABE Cross Project.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing,adaptation,distribution and reproduction in any medium or format,as long as you give appropriate credit to the original author(s) and the source,provide a link to the Creative Commons licence,and indicate if changes were made.The images or other third party material in this article are included in the article’s Creative Commons licence,unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visithttp://creativecommons.org/licenses/by/4.0/