地球磁层中合声波的扫频机制研究

滕尚纯，陶 鑫

1 同济大学海洋与地球科学学院，上海 200092

2 中国科学技术大学地球和空间科学学院，合肥 230026

0 引言

合声波是行星磁层中一种常见的哨声模式电磁波动.如果将该波动的电磁信号转换为声音信号，听起来如清晨群鸟的叫声，因而得名“合声波（chorus）”（Tsurutani and Smith,1974; Burtis and Helliwell,1976）.在地球磁层中,合声波对于能量电子的动力学行为扮演着诸多关键角色（Horne and Thorne,1998; Horne et al.,2005; Chen et al.,2007）.例如，合声波与几百 keV 的电子发生共振，可将这些电子加速至 MeV 量级（Bortnik and Thorne,2007; Reeves et al.,2013; Thorne et al.,2013）.这一过程被认为是磁层活动期间，辐射带电子通量增加的关键机制.合声波也可以与几百 eV至几 keV 电子共振，改变电子的投掷角，引起这些电子沉降入大气层，形成弥散极光（Thorne et al.,2010; Ni et al.,2016）.如果合声波的振幅受到准周期调制，则对应的极光形式为脉动极光（Nishimura et al.,2010）.正是因为合声波在能量电子动力学过程中扮演的关键角色，故研究者对合声波的科学兴趣持续了半个多世纪.

除了合声波对粒子的重要作用，合声波本身也具有两个典型的特征.其一，合声波的频谱通常具有双带结构，由频率约0.5fce的间断分割开来，频率在（0.1～0.5）fce的被称为下带波动，（0.5～0.8）fce的被称为上带波动，间断结构的成因至今仍充满争议（Maeda et al.,1976; Omura et al.,2009; Liu et al.,2011; Teng et al.,2019b）.其二，合声波的频谱展现出准周期性相干的扫频结构，每一个离散结构显示频率快速的上升或者下降，相对应的合声波被称为上升调或者下降调合声波（Tsurutani and Smith 1974; Li et al.,2012; Teng et al.,2019a）.

合声波被认为在磁赤道附近，约磁纬度3°以内产生（Santolik et al.,2004a,2004b; Agapitov et al.,2017; Teng et al.2018），其产生机制不同于闪电激发的哨声波.后者的频率变化是由传播过程中的波动色散所导致的.合声波扫频结构的激发机制是一个非线性过程.类似的扫频结构不仅出现在合声波中，磁层中的其他波动模式，如电磁离子回旋波（Pickett et al.,2010; Shoji et al.,2013）、磁声波（Fu et al.,2014）、聚变等离子体中的阿尔芬波均可以观测到扫频结构（Wang et al.,2018）.鉴于扫频结构的普遍存在性，理解合声波扫频机制的激发对于空间和聚变等离子体中广泛存在的现象具有重要的意义，本文将结合过去的相关观测以及模拟结果，重点回顾合声波扫频结构的激发模型.

1 合声波扫频结构的观测研究

合声波是内磁层中比较强烈的电磁波动，是相干的、有结构的哨声模波动.哨声模波动在内磁层等离子体条件下的色散关系近似为：

式中，n为 折射率，θ为波动的传播角度，Ωe为不加符号的电子回旋频率.当折射率趋向于无穷大时，波动会发生共振，此时对应的传播角称为共振锥角，是给定频率的波动所能达到的最大传播角度，形式为：

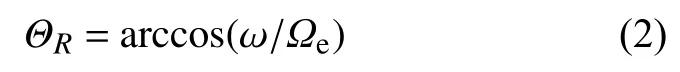
线性理论表明，在地球内磁层的等离子体环境下（β‖≥0.025），波动的最大线性增长率对应波动的传播角度为0°（Gary et al.,2012），即波动平行于背景磁力线传播.磁层观测统计发现，上升调合声波倾向于准平行传播，传播角度一般小于30°，上升调合声波的强度范围从几十pT 到几nT 不等；而下降调合声波是高度倾斜传播的，其传播角往往比较大（大于60°），甚至可能接近共振锥角，波动振幅相较于上升调要弱很多，主要集中在几十pT（Li et al.,2016; Zhang et al.,2018）.观测统计和射线追踪的结果均显示，合声波的传播角度会随着磁纬度的增加而增加（Bortnik et al.,2011; Agapitov et al.,2012）.

一般认为激发合声波的自由能主要来自于～10 keV 的具有温度各向异性的高能电子.尤其在亚暴期间，等离子体片中的电子从夜侧注入，自西向东漂移至日侧，各向异性的电子分布会逐渐形成，进而为合声波的激发提供了自由能，大量观测证实合声波的主要分布区域和能量电子的漂移轨迹是相吻合的（Li et al.,2009,2011）.图1 给出了由THEMIS 和Van Allen Probes 卫星共同观测到的合声波在L-MLT 平面内的全球分布情况（Meredith et al.,2020）.从中可以看出合声波的振幅会受地磁活动的影响，振幅通常为10～100 pT，在强地磁扰动期间，合声波的强度偶尔会达到1 nT.波动的分布具有明显的日夜不对称性，主要分布区域从夜侧至晨侧再至正午侧.在夜侧区域，合声波主要集中在磁赤道附近L<7 区域，而日侧发生率可以延伸到高纬度和L值比较大的区域.此外，下带波动的振幅明显高于上带合声波.

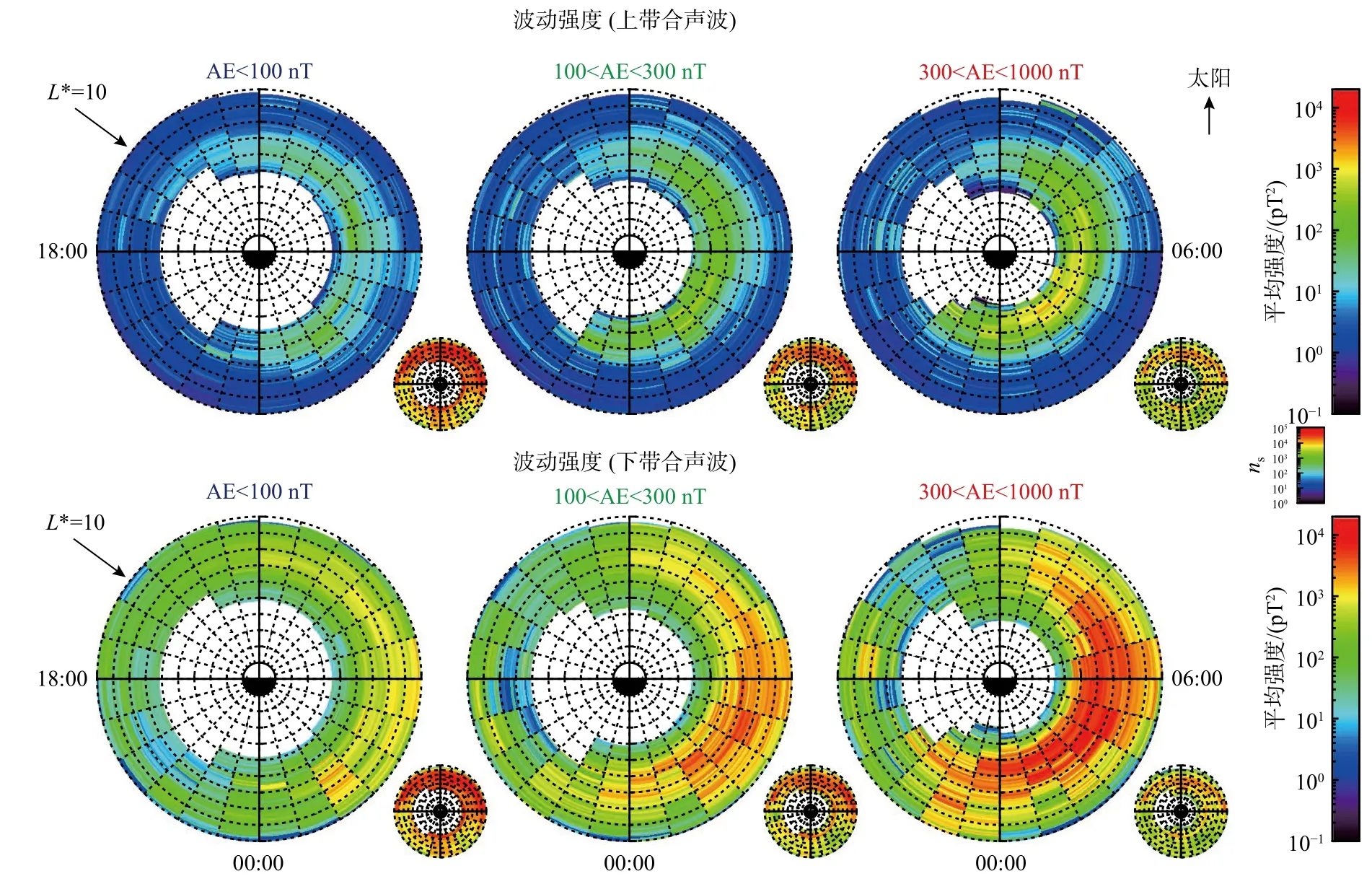
图1 上带和下带合声波在赤道区域（|λm|<6°）的波动强度分布图，不同列表示不同地磁活动强度.平均的波动强度随着磁壳数—磁地方时的变化在大图显示，小图表示相应的采样分布（修改自Meredith et al.,2020）Fig.1 The average wave intensity distribution of the upper and lower band chorus waves in the equatorial region (|λm|<6°).Different columns represent different geomagnetic activity conditions.The average wave intensity as a function of L-MLT is shown in large panels,the corresponding sampling distribution is shown in small panels (modified from Meredith et al.,2020)

分析合声波和粒子的非线性作用以及上升调扫频结构的激发机制，需要对波动的精细结构特征有充分的认识.合声波的精细结构特征主要包括振幅、扫频率、持续时长和重复周期等.这些特征在过去的统计研究中主要有：Macusova 等（2010）和Tao 等（2012）分别用Cluster 和THEMIS 卫星数据分析了合声波扫频率和背景等离子体参数的关系，研究发现合声波扫频率随着磁壳数的增加而降低，且日侧合声波的扫频率低于夜侧，具有明显的日夜不对称性；Shue 等（2015）用THEMIS 数据统计了上升调合声波的重复周期分布，研究表明夜侧和晨侧的重复周期小于日侧和昏侧，背景总磁场和温度是影响重复周期变化的主要因素；Santolik 等（2014）分析了波包的周期以及波包和波动振幅的关系；Santolik 等（2014）用范艾伦探测器分析了合声波精细结构中的波包和瞬时传播角.Teng 等（2017）应用Van Allen Probes 卫星分析了下带上升调合声波精细结构的持续时长，发现夜侧和晨侧的合声波精细结构普遍比日侧和昏侧持续时间短2～4 倍.模拟结果表明背景磁场的不均匀度是控制合声波持续时长与MLT 关系的一个重要因素.

2 合声波与电子相互作用的动力学过程

合声波的激发包含了线性和非线性增长两个过程.在合声波激发的初始阶段，线性增长起到了主要作用.Kennel 等（1966）提出对于平行传播的哨声模波动，波动增长的来源主要是具有足够温度各向异性的共振粒子，且增长率的大小由各向异性和共振粒子的多少决定.如果电子分布函数是具有温度各向异性的双麦克斯韦分布，当温度各向异性足够大且电子通量超过稳定捕获阈值时，回旋共振不稳定性便会发生.Kennel 等（1966）提出的简化线性增长率的计算为：

式中 ω是波动频率，VR是共振电子速度，η(VR)粗略地表示共振电子和总电子的比值，且：

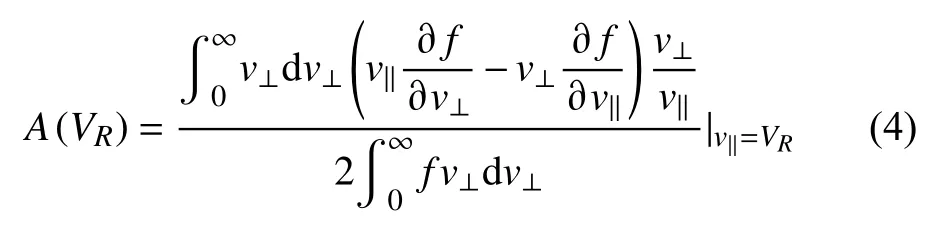
从增长率的公式可知，只有当A(VR)>时，合声波的增长率才为正值.线性理论预测了波动增长的初始阶段，如果经过线性增长阶段，波动振幅达到一定强度，共振电子会和波动发生相干非线性相互作用（Bortnik et al.,2008; Zhang et al.,2018,2019），从而产生合声波的扫频结构.

考虑沿着地磁偶极场传播的一支平行单色哨声波，波动频率为ω，波数为k，假定，其中 δB和B分别表示波动强度和背景磁场强度，ρ是特征回旋半径，那么在（v⊥,v‖,ζ）坐标系下，非相对论条件的洛伦兹方程可以表示为：

式中v表示速度，“‖”和“⊥”分别表示平行和垂直于背景磁力线的方向，变量 ζ 表示v⊥和 δB（波动振幅）的夹角，Ωw=eδB/mc.对于共振粒子，ζ会比 Ωe−1或者 ω−1在更长的时间尺度上缓慢变化.从波动相位的公式（7）可以看出，忽略与波动振幅相关的小项，回旋共振满足的条件可近似为：

其中，ω为波的角频率，v‖为速度平行于背景磁场的分量，k‖为波数平行于背景磁场的分量.当发生共振时，在相对于电子静止的坐标系中，多普勒频移后电磁波的频率（ω−v‖k‖）等于电子回旋频率，电子会受到相位不变的电磁力，进而会持续地发生速度变化.由于电磁场的变化周期与电子回旋运动的周期相当，所以电子很难保持绝热不变量的守恒，电子与电磁波会发生显著的能量交换，电子的能量或者投掷角发生变化，波的振幅也发生变化.考虑到共振粒子满足的共振条件vr≈(ω−Ωe)/k，则有：

结合上式（5～7），公式（10）可以改写成如下形式：

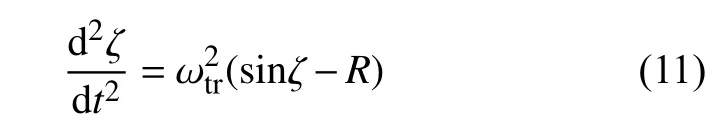
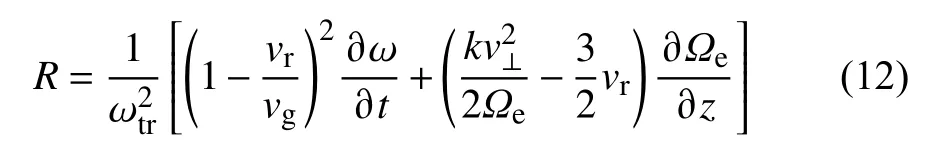
式中，vr为 电子的回旋共振速度，vg为波的群速度，z为沿着磁力线方向的长度.该式的推导和应用在很多探讨合声波激发的文章中给出（Vomvoridis et al.,1982; Omura et al.,2008）.

公式（11）类似一个单摆方程，其中包含附加项R.如果|R|<1，共振电子会存在两种类型的非线性行为，分别为：相位捕获（phase trapped）和相位聚束（phase bunched）.如图2 所示，相位捕获粒子是指这些粒子被波的势场捕获，共振粒子沿着闭合轨迹运动，可以在较长的时间（长于）和波场发生共振.对于这些粒子，它们会持续不断与波动交换能量和动量.相位聚束粒子是指沿着非闭合轨迹运动的共振粒子，这些粒子在分界面以外，只能在小于的时间与波发生相互作用.如果R>1，无法实现相位捕获，共振粒子的相位在[0,2π]之间变化.电子的行为如下图2、图3 所示.

图2 （a）当 R=0.5 时，波的势函数 V(ζ)=变化，其中=−∂V/∂ζ.水平虚线表示势井V(ζ)的最大值，边界处的ζ 用竖直虚点线表示.如果R>1，的符号总是和保持一致.（b）相位捕获（橙线）和未捕获（蓝线）共振粒子在相空(间的)运动轨迹，假定 ωtr 是常数，R=0.5，其中≡kv‖−vr/ωtr，黑色实线表示分界线（修改自Tao et al.,2020）Fig.2 (a) An equivalent wave potential function V(ζ)=with R=0.5,which satisfies =−∂V/∂ζ.The horizontal dashed line marks the maximum value of V(ζ) of the potential well,whose boundaries in ζ are indicated by the vertical dash dotted lines.It is clear that if R>1,the sign of is always the same as that of;therefore,it is monotonic and no potential well can exist.(b) An illustration of trajectories of phase trapped(orange line) and untrapped (blue line) resonant particles in phase space( assum)ing that ωtr is constant and R=0.5.Here ≡kv‖−vr/ωtr.The black solid line indicates the separatrix (modified from Tao et al.,2020)

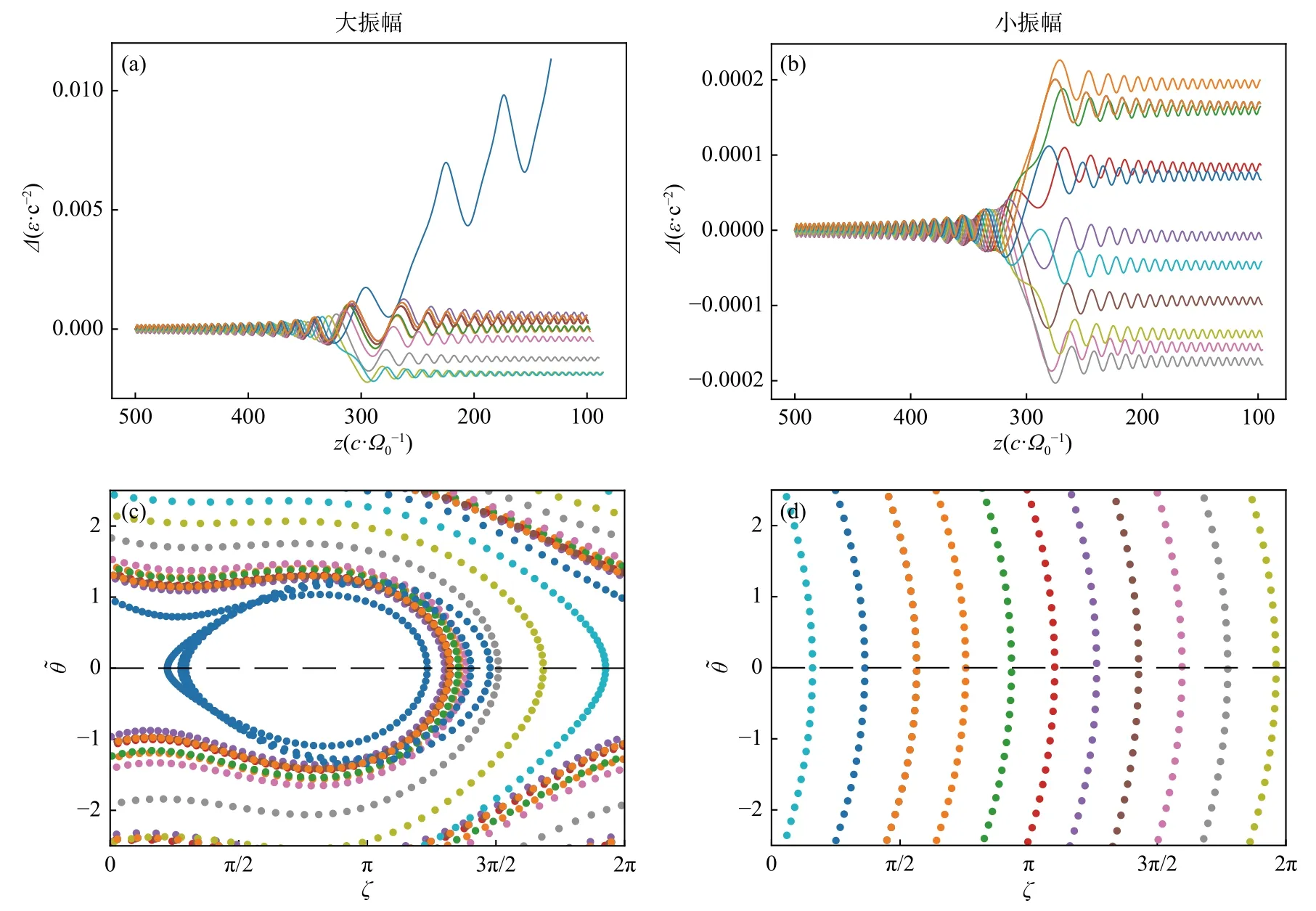
图3 （a，b）通过解洛伦兹方程[公式（5～7）]得到的12 个电子和单色哨声波发生作用的能量变化；（c，d）在共振时相应的相空间图.图（a，c）对应大振幅波动；图（b，d）对应小振幅波动.背景磁场满足 B=B0(1+az2)，电子初始能量满足共振条件，初始的相位在0 和 2π之间均匀分布.不同颜色表示不同电子的运动轨迹，对于图（a,c），蓝色线表示捕获电子的轨迹，其他电子是未捕获共振电子（修改自Tao et al.,2020）Fig.3 (a,b) Energy variation of 12 electrons (top rows) interacting with a monochromatic whistler wave obtained by solving Eqs.(5～7);(c,d) The corresponding phase space plot at resonance.Panels on the left column are for a large amplitude wave=2×10−3 with |R|<1 and those on the right are for a small amplitude wave =10−4 with |R|>1,where B0 is the magnetic field magnitude at z=0.The background magnetic field has the form B=B0(1+az2) with a=2.16×,where Ω0 the cyclotron frequency at z=0.The initial energy of the electrons are chosen to satisfy the resonance condition at z=300c/Ω0 with pitch angle of 150,and the initial ζ is uniformly distributed between 0 and 2π.Different colors indicate trajectories of different electrons.For panels in the left column,the blue lines are trajectories of phase trapped electrons,and other electrons are untrapped resonant electrons (modified from Tao et al.2020)

电子和波发生共振，相位捕获电子造成的直接结果就是相空间洞（或者坡）结构的形成（Nunn,1974; Vomvoridis et al.,1982; Omura et al.,2008,2021; Tao et al.,2017b），进而会引起共振电流JR的形成，−δj·δE表示粒子和波动的能量转移.共振电流由共振电子在相空间运动形式决定，受到R值的影响.测试粒子模拟结果显示当R大约在0.2～0.8 时，功率转移最大，而波动激发一般对应功率转移最大化的过程.图4 展示了Tao 等（2020）模拟出的一个上升调合声波和伴随出现的相空间电子洞结构.图4b 显示在v‖≈−0.15c和v⊥≈0.5c周围出现一个明显的低密度区，附近有一个高密度区，分别对应了相位捕获电子和相位聚束电子集中的区域.图4d 上相空间电子洞可以更明显地看出相位捕获电子运动的区域，即在平行速度分布函数图上，相空间电子洞导致v‖=0.15c附近出现明显的下降.

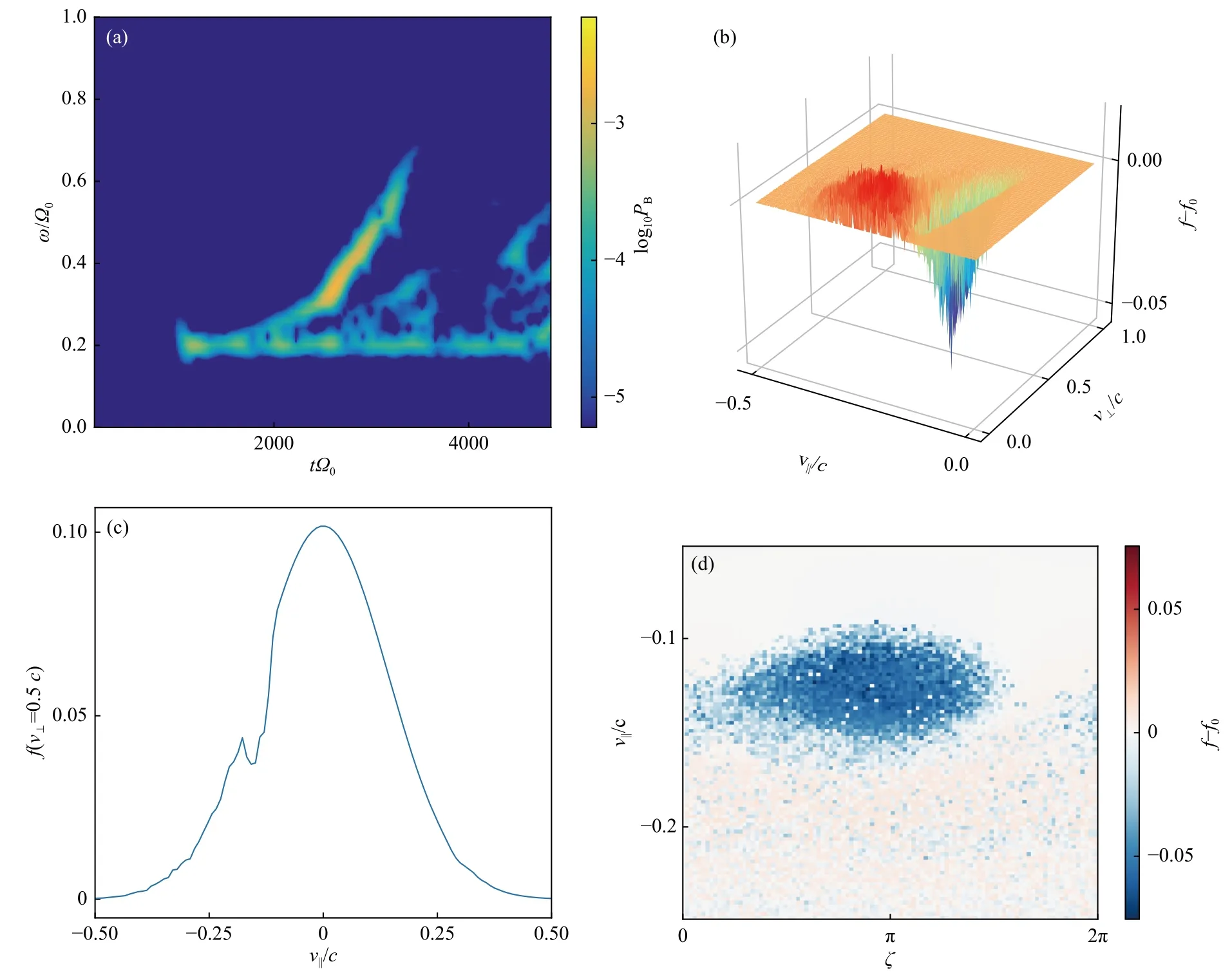
图4 和扫频结构相关的相空间结构示意图，模拟参数和模拟方法参考Tao 等（2017a）.（a）在磁赤道附近（z=0）波动的频谱图，颜色表示波动磁场的功率谱强度.（b～d）表示tΩ0=2 725处，电子的相空间分布，从中可见相位捕获粒子的洞结构的形成.（b）df=f(v‖,v⊥)−f0 的表面图，相空间洞出现在中心v‖≈−0.15c 和v⊥≈0.5c 区域.其中df>0 是由于相位聚束电子形成的.（c）f(v⊥=0.5c)随着 v‖的变化，相空间洞的位置大约在 v‖≈−0.15c.（d）f−f0 在v⊥=0.45c 处随着(v‖,ζ)的变化（修改自Tao et al.,2020）Fig.4 An illustration of the phase space structures associated with chirping elements.The simulation parameters and methods are from Tao et al.(2017a).(a) The frequency-time spectrogram of waves obtained using magnetic fields at equator (z =0).Colorcoded is the power spectral density of the wave magnetic field.Panels (b～d) show phase space distribution functions at tΩ0=2 725,with emphasis on the hole structure formed by dynamics of phase trapped particles.(b) The surface plot of d f= f(v‖,v⊥)−f0.The phase space hole is clearly seen with the center near v‖≈−0.15c and v‖≈0.5c.Those with d f >0 are due to phase bunched electrons.(c) f(v⊥=0.5c) as a function of v‖.Note the hole near v‖≈−0.15c.(d) f−f0 as a function of (v‖,ζ) at v⊥=0.45c.The boundary of this hole is similar to the separatrix in Figures 2 and 3.Note that f and f0 are normalized by the maximum value of f0 in this figure (modified from Tao et al.,2020)

3 合声波扫频的数值模拟模型

合声波的激发过程涉及波粒非线性相互作用，所以用数值模拟的方法研究其中的物理过程是必要的.在研究合声波激发问题上，有几个主要的数值模型.为节省计算资源，Nunn（1990）开发了弗拉索夫混杂模拟模型（Vlasov Hybrid Simulation,VHS），该模型使用宽频波作为触发波动，比粒子云模拟（Particle-In-Cell,PIC）更容易分离出主要物理过程，且更高效.但是该模型需要有输入波动，不能包括自然的饱和机制，因此不易研究从宽频哨声模波动到合声波的过渡状态.近年来，随着计算资源的快速发展，PIC 模拟逐渐应用起来.Katoh和Omura（2007）首次使用PIC 程序，成功模拟出了合声波.该模型是一维（1D）非均匀场下的电子混杂模拟，热电子和冷电子应用了不同的处理方法，热电子使用了粒子方法处理，为具有温度各向异性的双麦克斯韦分布，可以提供激发波动的自由能，冷电子使用流体方程处理.在边界条件的设置上，波动是被吸收的，而粒子是反射的.在考虑背景磁场对合声波激发的影响时，Katoh 等（2013）模拟了4 个算例，模拟程序固定了线性驱动，只改变背景磁场不均匀度.结果显示背景磁场不均匀度越小，合声波发生非线性增长和能够形成上升调合声波的阈值振幅就越小.该模型的成功对之后合声波模拟相关工作具有重要借鉴意义.Hikishima 等（2009）应用1D PIC 模型（KEMPO）重现了上升调合声波.Tao 等（2014）开发了DAWN 程序，并在之后应用了 δf方法（Tao et al.,2017a），可以更好地降低统计上的噪声，便于分析相空间结构与相关电子动力学过程.图5 是应用该模型，在磁镜场中不同垂直热速度条件下激发的波动频谱图（Tao et al.,2020），从上到下只有初始热电子垂直热速度（磁赤道处）发生变化，分别为（a）u⊥=0.32c,（b）u⊥=0.35c和（c）u⊥=0.6c，对应的热电子温度各向异性增加，从模拟结果可以看出，图5b 展示出清晰的上升调合声波，而图5a、5c 均没有出现清晰的分立合声波结构.由此可见，温度各向异性过弱或者过强都无法激发出清晰的合声波扫频结构.

图5 应用DAWN 程序得到不同线性驱动下的波谱.三个模拟结果都是采用和Tao 等（2017a）相同的模拟参数，除了应用不同的垂直电子温度.其中（a）u⊥=0.32c；（b）u⊥=0.35c；（c）u⊥=0.6c（修改自Tao et al.2020）Fig.5 The wave spectrum with different linear drive from numerical simulation using the DAWN code.All three simulations use similar parameters to that of Tao et al.(2017a),except the perpendicular thermal velocity ut⊥.H ere we use (a)ut⊥=0.32c,(b)ut⊥=0.35c,and (c)ut⊥=0.6c,with c the speed of light in vacuum.Correspondingly,the linear drive increases from case A to case C (modified from Tao et al.2020)

在真实磁层环境下，合声波往往不是平行于磁力线传播，而是具有一定的传播角，因此，研究内磁层中斜传播的合声波激发过程需要考虑二维的磁镜场或偶极场.Ke 等（2017）以及 Lu 等（2019）开发了二维一般曲线坐标系下的粒子模拟程序，成功模拟了合声波在磁镜场和偶极场下的激发和演化.

4 合声波扫频的理论模型

4.1 Helliwell 模型

合声波扫频结构的激发机制从1960 年代就进入激烈的讨论，其中一个经典的理论模型是Helliwell（1967）模型.该模型从不均匀背景磁场的角度解释了合声波扫频的产生.为了保持波和粒子耦合时间以及波动强度的最大化，Helliwell 假设波动频率的改变与背景场强的变化一致使得共振条件始终满足.在背景磁场随着位置变化的条件下，电子的回旋频率和多普勒频移后的波动频率保持一致，从而波动频率会发生变化.合声波的扫频率可以通过求解粒子的绝热运动方程、合声波的色散关系以及回旋共振条件得到.对于该模型，合声波的扫频率和热电子分布没有关系，仅和背景参数相关，因此可以完全使用背景等离子体参数（如背景磁场位型、电子密度等）来估算空间某个位置合声波的扫频率.

过去对于合声波扫频率的观测统计结果（Macusova et al.,2010; Tao et al.,2012; Shue et al.,2015; Teng et al.,2017）与Helliwell 的理论预测具有很好的一致性.图6 为Tao 等（2012）利用THEMIS 卫星数据得到的合声波扫频率空间分布.从中可以看出：（1）合声波的扫频率随着磁壳数的增加而降低.利用Helliwell 理论定性的理解这一现象，即为合声波的扫频率会随着背景磁场不均匀度的减小而降低，距离地球越远，背景磁场越均匀，扫频率越低.（2）合声波的扫频率具有明显的日夜不对称性，日侧合声波的扫频率低于夜侧.这是由于日侧磁层顶被太阳风压缩，磁层位型相较于同距离的夜侧磁场更均匀，因而日侧合声波的扫频率更低.

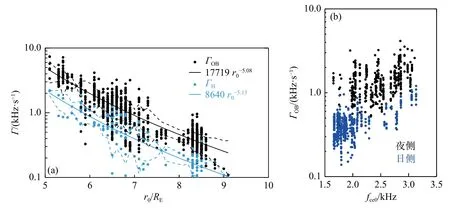
图6 （a）合声波观测的扫频率（黑点）和Helliwell（1967）理论计算扫频率（蓝点）对比.实线为理论计算结果.（b）日侧和夜侧观测的合声波扫频率对比（修改自Tao et al.,2012）Fig.6 (a) The comparison between the observed frequency sweep rate (black dots) and the theoretical frequency sweep rate (light blue dots) from Helliwell (1967).(b) The comparison between the observed frequency sweep rate from dayside (MLT>8 h,blue dots) and dawnside (MLT<8 h,black dots) (modified from Tao et al.,2012)

基于相同的扫频机制，Sudan 和Ott（1971）提出另一个更加定量的模型.在该模型中，激发波动的捕获电子会形成相位相关的电流，造成不稳定性，进而形成新的波动.作者从理论上分析了这些不稳定性造成的波动增长率.

4.2 连续触发模型

Nunn（1971,1974）分析了相位捕获粒子和窄带波动的动力学方程，相位捕获的粒子和波场发生作用之后，其能量和磁矩会经历较大的变化.由Liouville 定理可知，经过几个共振周期之后，捕获粒子的相空间密度会明显区别于周围的其他粒子，对共振电流密度起到了主要的贡献.根据这些分析，作者开发了Vlasov 混杂模型，可以用于模拟上升和下降调合声波（Nunn,1990; Nunn et al.,1997）.

Vomvoridis 等人研究在非均匀磁场、给定波场条件下，相位相关的测试粒子、波动的非线性（Vomvoridis and Denavit,1980），以及合声波扫频等问题（Vomvoridis et al.,1982）.Vomvoridis和Denavit（1979）展示，在|R|<1的条件下，捕获粒子会产生相空间洞/岛，造成比较强的相位聚束分布.Vomvoridis 和Denavit（1980）把非均匀场下波动的增长/阻尼率分为三个部分：γ0、γ1和 γ2.其中 γ0表示类似在均匀场下的影响，增长率通常在几个之后达到饱和，作者推断该增长率最后不会造成较大的波动增长.增长率 γ1表示非均匀场对未捕获电子的影响，大小和线性增长率在一个量级.γ1不会饱和，因为在非均匀场下，共振区域会连续不断地被新的未捕获粒子填充. γ2是最为重要的增长率，表示由于密度和v⊥差异造成的影响.Vomvoridis等（1982）指出当R趋向于0 时，增长率 γ2会消失，对于有效的非线性增长，R的范围应该是0.2≤|R|≤0.8.作者进一步分析了带有扫频的合声波事例，结果表明对于最大的波动放大，|R|～0.5，扫频率和波动振幅成正比，即为：

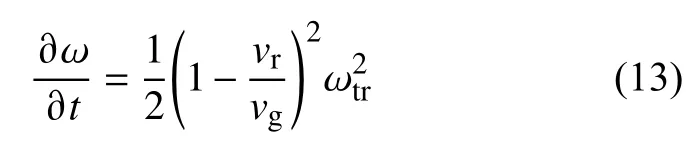
对于（13）式，由于合声波激发区域在赤道处，故∂Ωe/∂z≈0.这个关系在之后的Omura 等（2008,2021）和Zonca 等（2017）工作中也被用不同的方法推导得出.

在另一系列工作中，Omura 等（2008）假定相位捕获电子分布函数的密度恒定，用分布函数的解析形式来研究合声波的激发.作者计算了平行于电场的共振电流（JE）随着R的变化，发现在R=0.4 时，JE可以达到最大值，此时，向波动传输的能量也达到最大（−JE·δE）.通过推导哨声波的非线性增长率以及合声波激发的最小阈值条件，作者提出扫频是由于非线性电流的非线性频率漂移造成的，并获得了扫频率和波动振幅的关系.Omura 和Nunn（2011）提出连续激发模型，并用VHS 程序研究了平行于磁场的电流（JB），通过非线性共振电子形成的JB来解释扫频的结构.

Trakhtengerts（1995）提出用Backward Wave Oscillator（BWO）模型来解释合声波，在该模型中，粒子分布在平行方向较大的梯度会造成合声波的增长.与其他合声波模型不同的是，BWO 模型能够预测合声波精细结构的重复激发性质.Demekhov等（2017）根据BWO 理论模拟了合声波的激发，与THEMIS 观测的扫频率、波动振幅以及精细结构重复周期具有非常好的一致性.但由于粒子数据在投掷角和能量方向的分辨率有限，所以粒子数据的阶梯特征尚未有观测的证据，分布函数的不连续性在一些工作中也被质疑（Nunn and Omura,2012;Shue et al.,2015）.

对于公式（13），计算 ωtr的波动振幅是波动激发时的振幅，而在源区观测到波动是非常困难的，且波动在远离源区、向外传播的过程中，振幅会发生剧烈变化，所以统计上直接比较扫频率和观测的振幅以证明公式（13）往往比较困难.尽管如此，Cully 等（2011）用THEMIS 数据分析了一个事例，展示对于不同的合声波精细结构，扫频率会随着波动振幅的增加而增加.Kurita 等（2012）用无间断的合声波结构展示扫频率和上式预测一致.

4.3 TaRA 模型

尽管合声波的不同激发模型在不同方面有其合理之处，但是扫频过程中的各种问题仍然存在.首先，根据Helliwell（1967）及Sudan 和Ott（1971）的理论，假定扫频是由背景磁场的不均匀度导致，那么均匀磁场中的扫频（Wu et al.,2020）以及BWO 的模型结果（Demekhov and Trakhtengerts,2008）则无法解释.其次，扫频率要么是背景磁场不均匀度（Helliwell,1967），要么是波动振幅（Vomvoridis et al.,1982; Omura et al.,2008; Zonca et al.,2017）的函数.这两个扫频的估算方式完全不同，但彼此都有相应观测和模拟的验证支持（Hikishima et al.,2009; Cully et al.,2011; Katoh and Omura,2011）.根据粒子模拟中波动增长率、电子的相空间动力学以及非线性波粒相互作用理论，最新提出的TaRA（Trap-Release-Amplify）模型实现了对过去几类主流模型的统一（Tao et al.,2021）.该模型根据波动传播方向，将空间中赤道附近区域（波动源区）分成上下游，两个区域在波动激发中分别扮演不同的角色.波动在上游产生，向下游传播，在下游区域，非线性波粒相互作用形成了相干的电子相空间结构；而在上游区域的释放点，当粒子与波动满足相位锁定条件时，波和粒子能量交换达到最大化，使得该相干相空间结构通过选择性激发过程，产生具有扫频的合声波.

图7 为该模型示意图，蓝色波形为模拟中对一给定时刻的合声波波形沿着背景磁场的分布.假定合声波包含了近乎连续频率（ω0,ω1,ω2,...）的哨声模波谱，这些频率之间的间隔非常小，可以认为产生这些波包是由频率从 ω0到 ωN组成.对于上升调扫频结构，起始频率是 ω0，终止频率是 ωN.由于共振电子和波动的运动方向相反，较新电子首先和较早产生的频率为 ω0的合声波在下游发生共振作用.这些电子朝向上游运动，在共振过程中会被相位捕获，产生“相位聚束”电流.当电子运动到上游，波动振幅太小而不能继续相位捕获粒子的时候，这些共振电子会被释放.由于这些电子和波动仍然是相位相关的，一旦释放，它们仍然可以从宽频哨声波谱中选择性放大一些新的波动.挑选的原则是使共振条件可以最长时间地满足波和粒子能量转移最大化.为了方便下文讨论，在此分别定义R1和R2，以区分背景磁场不均匀度和扫频率.

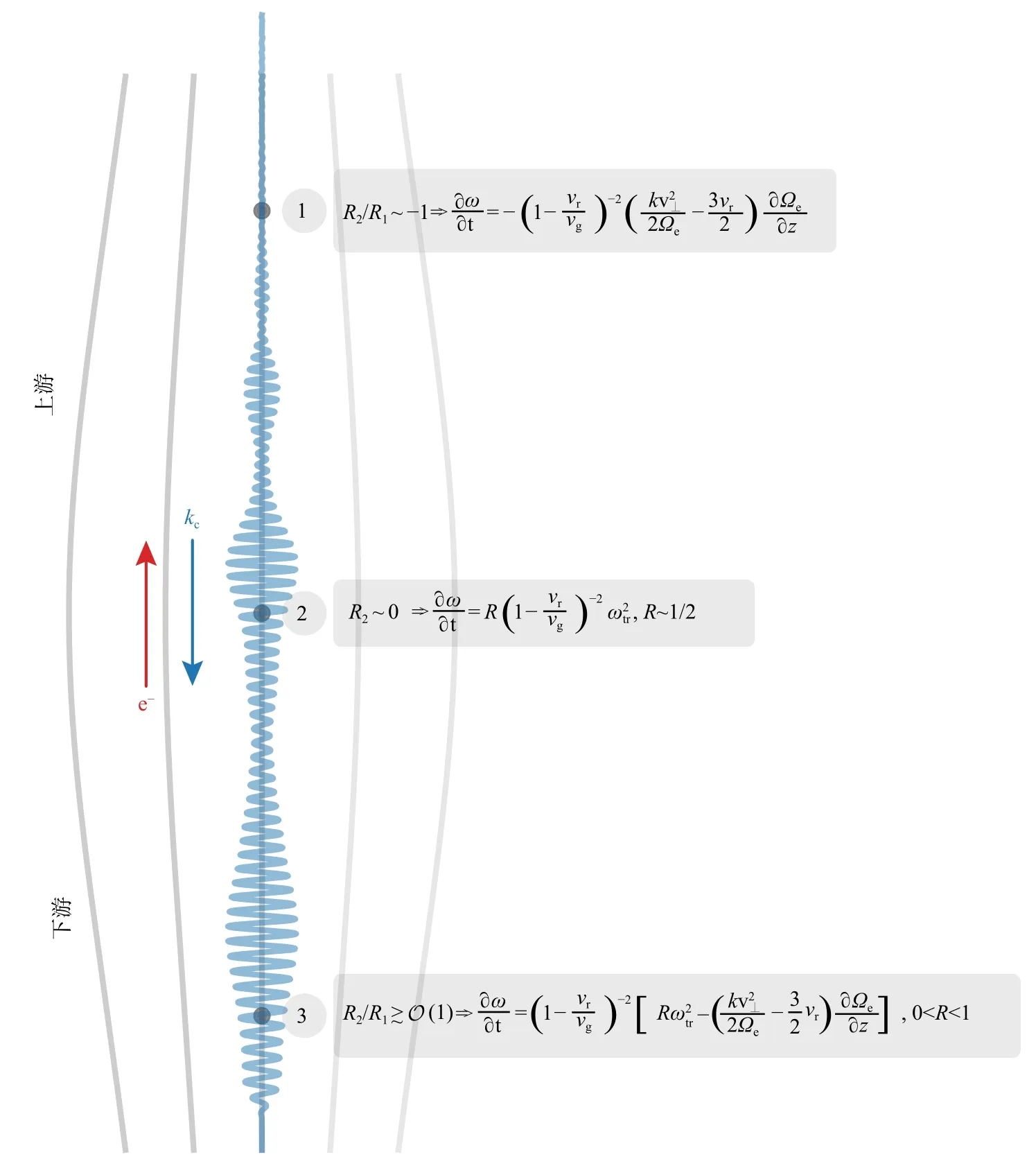
图7 TaRA 模型示意图.红色箭头标识了共振电子的运动方向，蓝色箭头表示合声波波失的方向.蓝色波形是从模拟中得到的，1、2、3 点分别代表释放点（R2≫）、赤道处（R2=0）以及下游处的某点[R2/R1≳O(1)].不同位置相应扫频率的计算分别在对应位置给出（修改自Tao et al.,2020）Fig.7 Illustration of the TaRA model.The red arrow indicates the motion of resonant electrons (e−),while the blue arrow indicates the direction of wave vector (kc) of chorus.The blue waveform is taken from simulation.Points 1,2,3 represent the release point (R2≫),the equator (R2=0),and a point in the downstream where R2/R1 ≳O(1).The corresponding equations for the chirping rate are also given at the three points (modified from Tao et al.,2020)

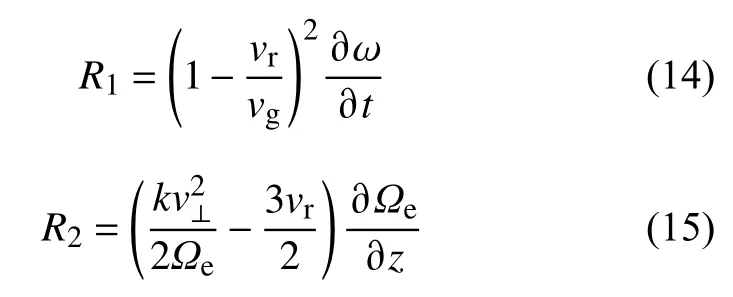
R1表示扫频率的影响，R2表示是背景磁场不均匀度.

根据这个模型，可以在不同位置估算合声波的扫频率.首先，在释放点（即图7 中的点1）新的波动被激发，波动振幅项远远小于不均匀度项R2.与之对应，相位锁定条件需要−R2和R1达到平衡，即为：

从而

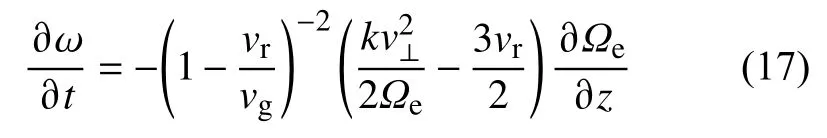
上式定义了扫频率和背景磁场不均匀度的关系.对于磁层中的上升调事例，上游区域负的背景磁场不均匀度是上升调扫频的原因.上游区域波动强度较弱，由产生波包造成的非线性相位捕获电子主要出现在下游区域.在赤道附近，R2～0（对应图7中的点2），根据Vomvoridis 等（1982）的研究，有效波动能量传输主要发生在R的值在0.2～0.8之间.为了简化，R通常取0.5，而Omura 等（2008）通常取R=−0.4.这样就会得到著名的扫频和波动振幅的关系：

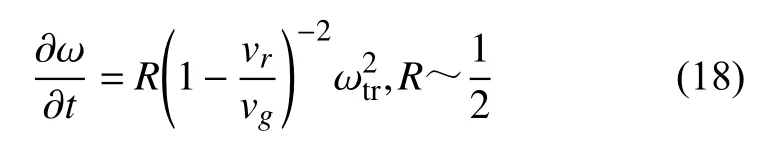
在此需要强调，新的合声波是在上游区域，即图7中点1 产生的，而不是赤道位置.所以公式（17）描述的是扫频如何产生，以及为什么在这种情况下是对应上升调；然而公式（18）则强调合声波激发区域，波和粒子非线性作用的重要性.最后，在下游的3 点，R2和R1相当甚至更大，不均匀度对于R的贡献不能忽略，最后会导致扫频率的如下计算：

从以上描述可知，TaRA 模型和之前提出的模型具有一致的原则，即非线性波粒相互作用导致窄带扫频波动的产生，而不同模型的差别在于如何应用这些准则解释扫频率以及合声波的结构.TaRA 模型首次提出：不同模型的主要差别在于他们是在合声波激发的不同阶段推导波动扫频率，统一了过去看似不相关的理论模型.

TaRA 模型除了实现过去理论模型的统一，还可以对合声波精细结构、窄带特性，以及演化过程提供合理的物理解释.合声波精细结构的波形通常展示出图8 所示的振幅准周期性调制，即所谓的子波包结构（subpacket），Santolik 等（2014）推测这些子波包可能是由一系列窄带波动叠加形成，或是在激发过程中形成.Omura 和Nunn（2011）提出这些子波包是通过一系列触发过程形成的，在合声波激发过程中，触发波动会造成电子的相位聚束和相位捕获，非线性共振电流形成，进而会产生更高频率的新波动，形成子波包.如果波动振幅足够大，新形成的频率较高波动会继续相位聚束新的电子，造成进一步的扫频和更多子波包的形成，所以子波包在该理论中被认为是合声波扫频的基本单元.Tao 等（2017b,2021）用O'Neil 等（1971）的理论解释了子波包的形成，在该理论中，子波包结构可以用波场和相位捕获电子的动量和能量守恒来解释.当相位捕获电子在相空间旋转，其速度、动量会以的周期振荡，自然会造成波动振幅以振荡，形成子波包（subpacket）结构.

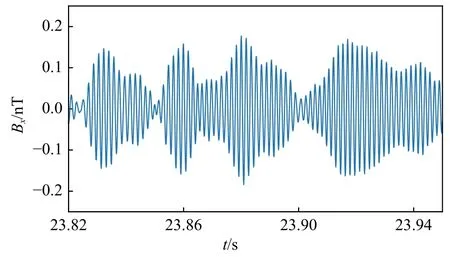
图8 合声波磁场分量波形图，其中展示了准周期性振幅调制，形成了合声波的“子波包”（修改自Tao et al.,2020）Fig.8 An example of Bx-waveform showing quasi-periodic amplitude modulation,forming "subpackets" of chorus waves (modified from Tao et al.,2020)

5 总结与展望

合声波扫频结构的激发是一个典型的非线性等离子体物理问题，理解这个过程有助于深入认识空间等离子体波粒相互作用.本文概括了合声波扫频结构的观测特征、数值模拟以及主流的理论模型，并重点介绍了最新提出的“TaRA”模型，该模型不仅实现了过去模型的统一，还为合声波的观测和模拟现象提供了合理的理论解释.该模型是基于偶极场条件下上升调合声波的PIC 模拟提出来的，对于均匀场下合声波的扫频结构，下降调合声波，以及电磁离子回旋波的扫频问题都有重要的借鉴意义.此外，其他行星（如火星、木星和土星）空间中的合声波扫频性质（Hospodarsky et al.,2008;Menietti et al.,2013,2014; Harada et al.,2016）也有助于检验和拓宽该模型.