田间长波路面不平度表达和分级的新方法

程远盛， 李晓勤， 孙帅帅， 满晓兰， 范非凡， 李志雄

(1.塔里木大学 机械电气化工程学院，新疆 阿拉尔 843300； 2.塔里木大学 现代农业工程重点实验室，新疆 阿拉尔 843300； 3.中国科学技术大学 精密机械与仪器系 中国科学院材料力学行为与设计重点实验室，合肥 230027; 4.延世大学 延世前沿实验室,首尔 03722)

田间路面不平度是影响田间农用机械作业质量[1]，车辆平顺性以及通过性的重要因素[2]。同时也会引起车辆振动，导致零部件疲劳损伤，降低农用车辆的使用寿命[3]。然而，车辆在田间行驶时，较短波长的路面会形成车轮包络，使轮胎—地面系统的相对阻尼增加[4]，难以引起车辆的振动。而波长的增加会增大对车辆的瞬间激励，且引起车辆较大振动强度的原因主要为长波路面的激励[5]。随着我国农业机械化的快速发展，农业机械作业量上升，所以需要一套田间路面不平度测量装置，对田间长波路面的表达和分级进行探究。

传统的测量方法能够测得原始不平度和车辙不平度，却难以得出田间路面的有效不平度，既有效的激励形式[6]。由于车辆振动加速度响应是路面给与位移激励的一种反馈形式，在得知车辆自身力学结构和加速度响应的情况下可以反求路面位移激励[7]，因此逐渐应用到路面不平度的测量中。如Lak等[8]、Pawar等[9]、Wang等[10],均建立了车辆振动响应模型，进行了公路路面振动试验，分析得出路面不平度，证明了运用车辆振动响应估计路面不平度的有效性。Zhang等[11]在求得车辆加速度响应的同时，结合小波变换对桥梁路面不平度进行了重构，为桥梁路面的实时检测提供了帮助。Xue等[12-13]建立车辆-路面系统振动方程，运用车辆振动响应信号进行分析，求出道路中坑洞的尺寸，为公路硬路面的养护提供了较大帮助。以上均为路面不平度的估计提供了有效的建模理论和试验方法，但是每种车型均有自身的力学结构，导致通用性较差难以广泛使用。Bidgoli等[14]设计了一套公路路面振动采集系统，可以运用不同种车型为动力进行不同硬路面的测量。但是测试轮和测试台架尺寸较小，导致通过性较差，难以在野外应用。由于土壤的力学特性易受环境改变，车辆在不同的田间路面行驶时会受到不同的阻力。因此硬路面的车—地系统模型，难以在田间路面运用。

本文针对田间长波路面不平度的测量设计了一套田间软路面不平度的测试系统，并通过对不同长波路面进行测量，对田间长波路面不平度的表达和分级进行了探究。主要运用车辆产生的振动加速度来反求田间软路面的有效不平度，并设置不同尺寸的矩形坑路面，模拟不同长波的田间路面，动力由土槽实验室的牵引车提供。建立车辆-软路面系统方程，得出软路面有效不平度模型，通过锤击试验和模态分析得到有效不平度模型的力学参数。将得到的有效不平度进行空间功率谱密度(PSD)分析，得出不同路面的激励特性。最后结合ISO 8086[15]对路面进行分级。为土壤软路面有效不平度的测量提供了新方法，同时为进一步建立典型的，如犁地、耙地，等土壤软路面的路谱做铺垫工作。

1 材料与方法

1.1 测试系统与路面构造

整车自由度过多会相互干扰影响测试结果，也会增加测试系统模型的复杂程度，因此采用了单自由度设计，同时为了增大通过性采用了实车轮组，测试系统如图1(a)所示。其中轮胎选用山岭公司的825R16全钢丝子午线轮胎，气压为0.5 MPa。采集仪型号为WS-5291、信号放大器型号为WS-2401、信号采集软件为Vib‘SYS，加速度传感器型号为BZ1124，均为北京波普公司生产。其中加速度传感器Z轴方向(垂直方向)灵敏度为6.234 pc/ms-2，频响范围为0.2～8 kHz。车轮垂直方向的总质量m为103.5 kg。牵引车动力由电机提供，并有独立的轨道，运行过程中振动较弱，所以忽略对测试系统的干扰。

(a) 测试系统

(b) 路面构造图1 测试系统和路面构造Fig.1 Test system and pavement configuration

由于田间路面具有极易变形的特性，且每块田间路面都是独立的一种地形，导致路面难以统一。所以本文需对路面进行构造，用于限定路面。主要是将软路面设置为不同激励幅值和不同激励频率的长波路面，用于探究田间长波路面表达和分级的同时，通过求解得出的位移激励频率和空间功率谱密度的峰值点验证该方法的有效性。

试验地点为塔里木大学土槽实验室(经度：81.297 248、纬度：40.544 428)，选取土槽面积为5×30 m2，土壤为干旱性土壤[16]。对修整后的场地进行土壤坚实度测量，土壤坚实度仪器型号为TJSD-750-Ⅱ。将试验场地均匀分为7列3行,共21个点，每个点进行三次测量，三次测量的深度分别为10 cm、20 cm、30 cm，测得数据如表1所示。为了构造不同长波的路面，将矩形坑的深度和跨度设为变量；深度分别为10 cm、20 cm、30 cm，用于改变激励的幅值。跨度分别为10 cm、20 cm、30 cm、40 cm、50 cm、60 cm、70 cm，用于改变激励的频率(波长)。宽度固定为30 cm，两坑之间的距离固定为60 cm。将同一深度和跨度的10个矩形坑路面定义为一种路面，共分为21种。如图1(b)所示。

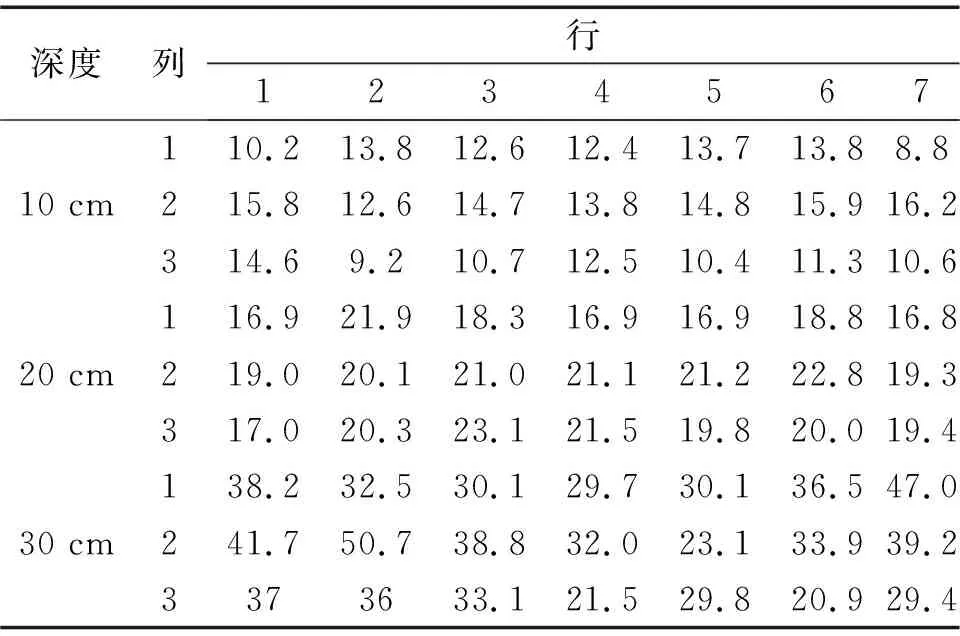
表1 坚实度测试统计表Tab.1 Statistics table of Solidity test kg/cm2

1.2 田间长波路面分级方法

本文以测试台架响应为输出，反求土壤软路面有效不平度。主要包括：① 建立车辆-软路面系统振动方程，得到有效不平度模型，并找出模型的未知参数，包括垂直方向的等效刚度、等效阻尼、速度信号、位移信号;② 通过锤击试验并进行模态参数识别得出等效刚度和等效阻尼；③ 对加速度信号进行一次积分和二次积分，得出车轮垂向的速度和位移信号；④ 对得到的有效不平度进行空间功率谱分析。

1.2.1 有效不平度模型

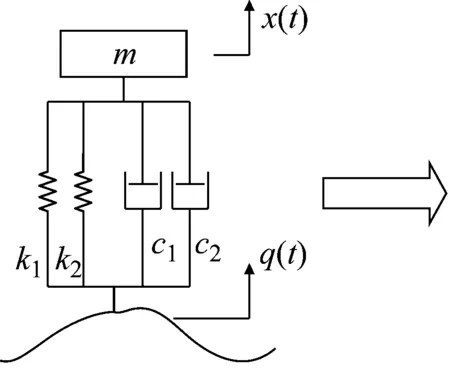
测试过程中，设车轮受地面激励均匀对称，且土壤自身刚度和阻尼也会影响车辆振动特性。因此将车辆—地面系统的刚度和阻尼，在垂直方向上作等效叠加[17]，系统简化过程如图2所示。

(a)

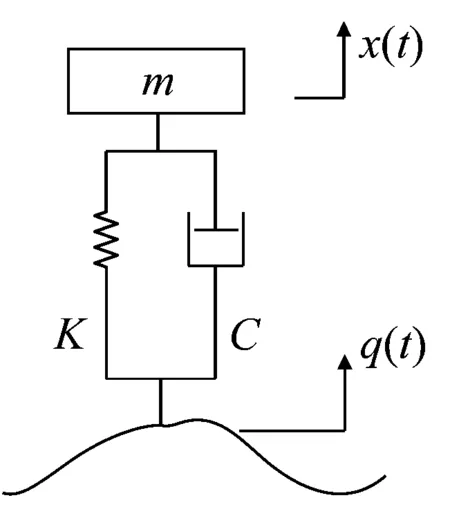
(b)k1-土壤垂向刚度;k2-轮胎垂向刚度;c1-土壤垂向阻尼;c2-轮胎垂向阻尼;x(t)-车轮上下位移;q(t)-有效地面位移输入;K-系统垂向等效刚度总和;C-系统垂向等效阻尼总和。图2 车辆-地面系统模型简化Fig.2 Simplified of vehicle-ground system model

图2(a)为实际振动系统模型，图2(b)为简化后的振动模型。模型中K=k1+k2，C=c1+c2。q(t)为地面有效不平度输入激励，建立振动微分方程如式(1)所示。

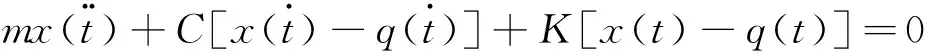
(1)

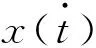
对垂向位移求解可得

(2)

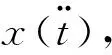
1.2.2 等效刚度、阻尼求解

设计锤击试验进行测试，将力锤产生的信号作为激励力信号，加速度传感器测得信号作为响应信号；将加速度响应信号的拉普拉斯变换与激励信号的拉普拉斯变换之比作为系统响应，即传递函数[18]。选取特征值进行参数识别，得出系统力学参数。

如图3所示，传递函数曲线实部和虚部均有5个峰值点，选取实部为0虚部最高的峰值点频率，进行模态参数识别，得到系统得固有频率ωn和阻尼比ξ，采样频率为5 000 Hz。对7次试验测得的固有频率和阻尼比进行均值处理，得到平均固有频率ωn值为 211.899 8 Hz，平均阻尼比ξ=1.16%,如表2所示。各参数之间关系如式(3)和式(4)所示。因此得出垂直方向等效刚度K为4 647 307.86 N/m，等效阻尼系数C为508.813 8 N·s/m。

(a) 锤击试验

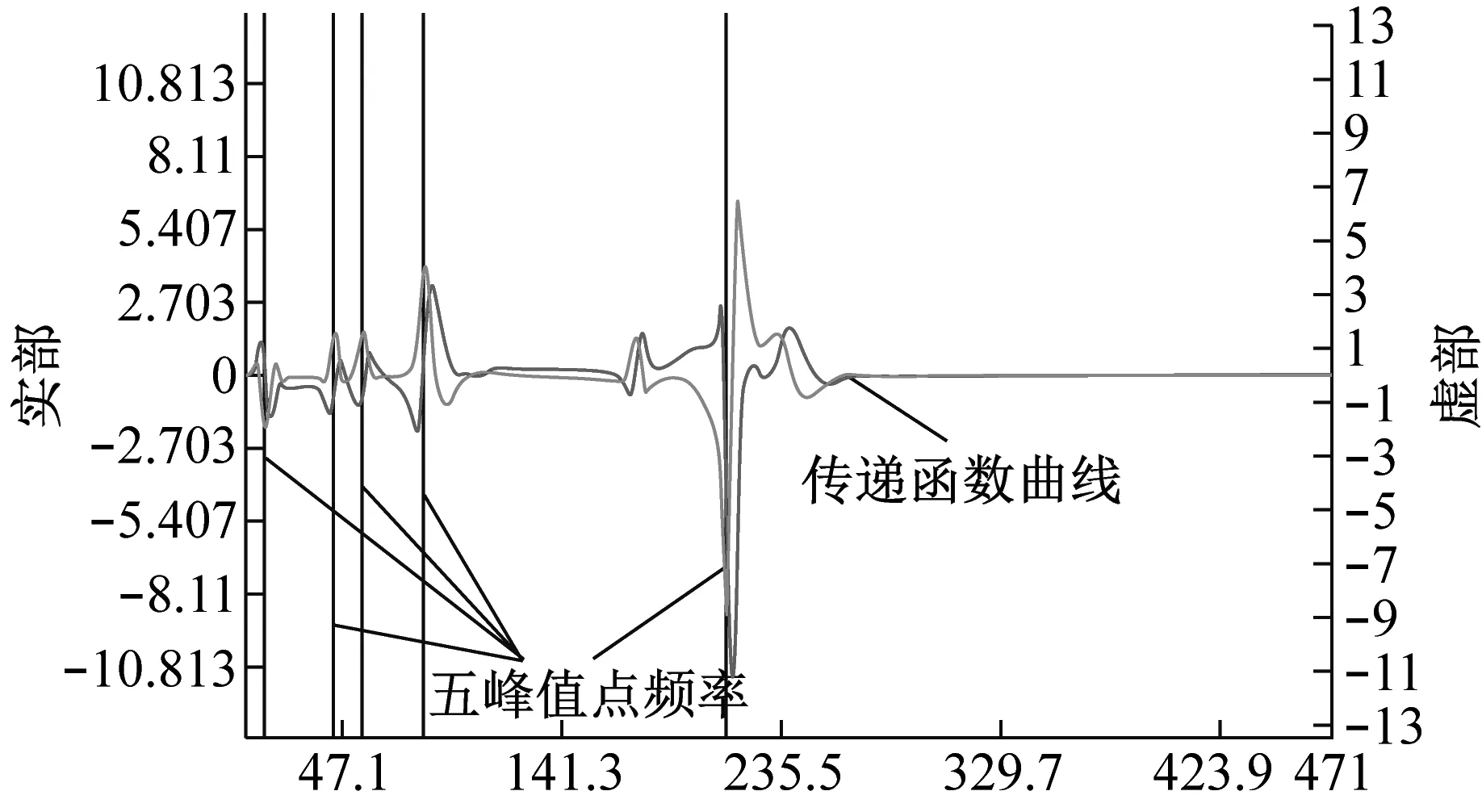
(b) 模态参数识别图3 锤击试验示意图Fig.3 Schematic diagram of hammer test

表2 车辆-地面系统五阶振型对应的固有频率计算结果Tab.2 Calculation results of natural frequencies corresponding to the fifth-order mode of vehicle-ground system Hz

(3)

(4)

1.2.3 车轮垂向位移信号和速度信号的求解

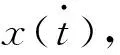
(5)

二次积分得到位移信号频谱为

(6)

其中

(7)

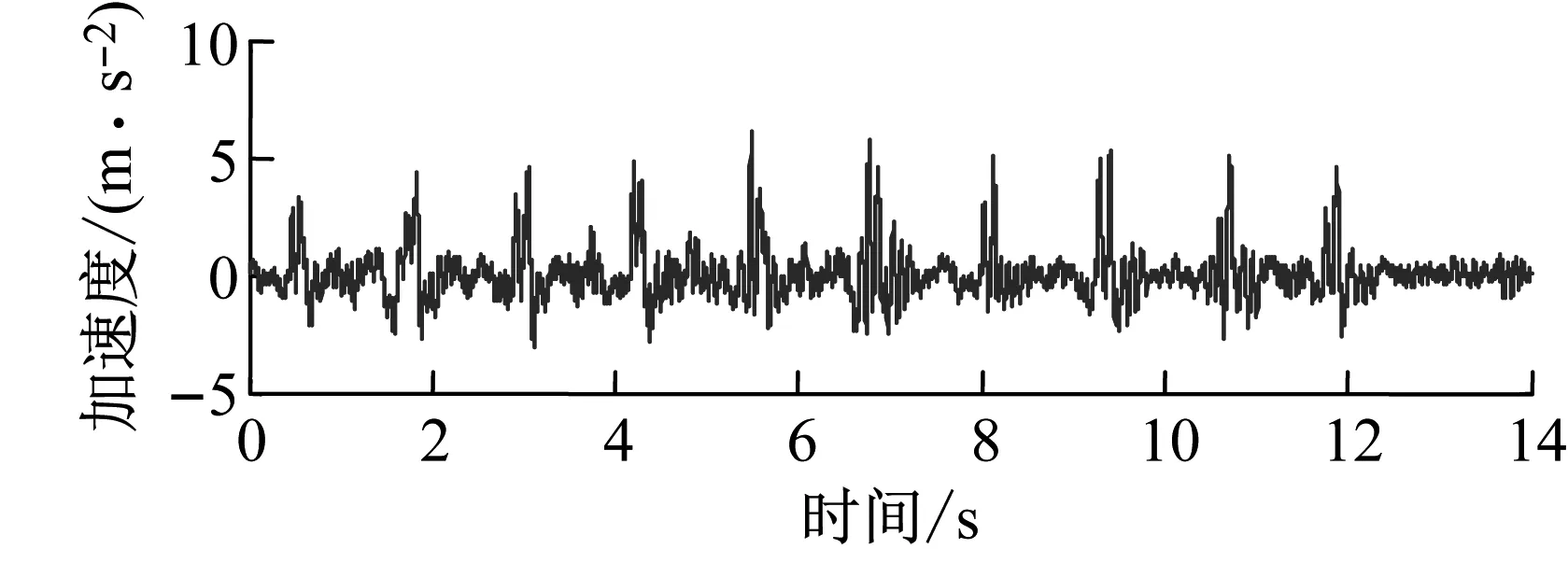
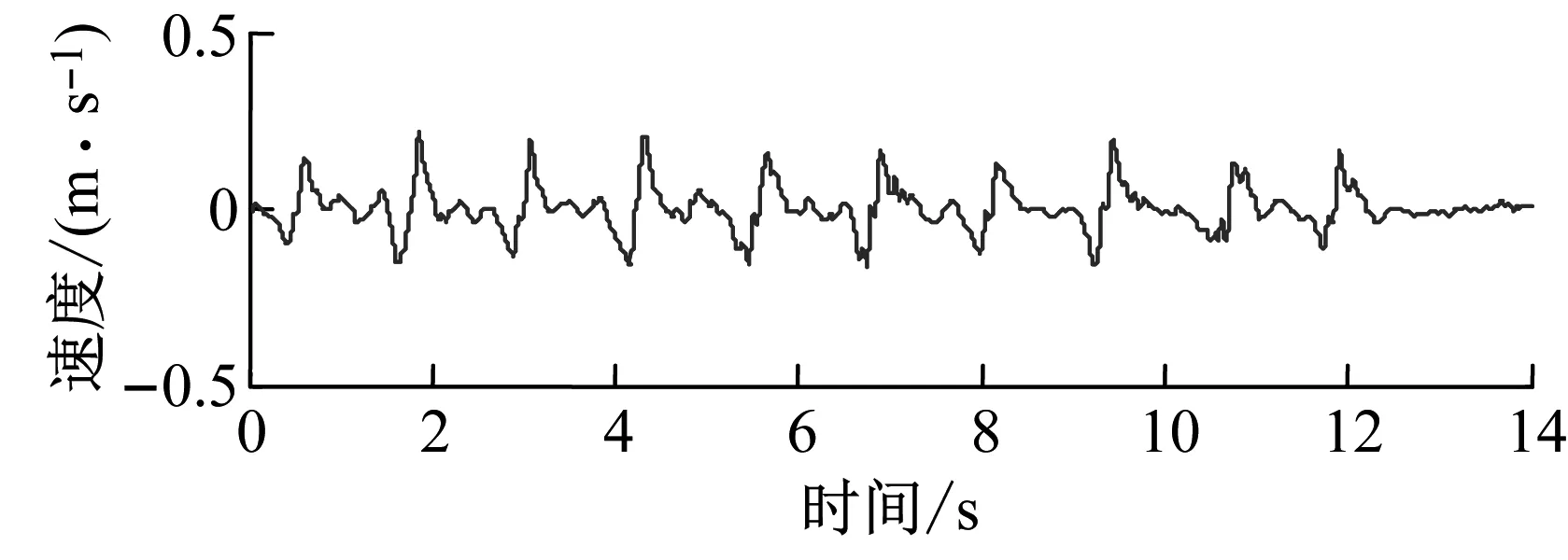
图4 振动加速度信号一、二次频域积分时域图Fig.4 First and second frequency domain integral time domain diagram of vibration acceleration signal

1.2.4 路面不平度等级划分

本文采用软路面有效不平度功率谱密度(PSD)的方法对路面进行评价，以上建立了有效不平度模型，并结合式(3)～(7)求出q(t)所需参数，则软路面有效不平度进行功率谱密度计算公式如式(8)所示。

(8)

式中:PSD(f)为有效不平度的功率谱密度，单位为m3；L为数据长度；f为时间频率，单位为Hz；j为虚数单位。继续对有效不平度功率谱密度进行双对数运算，得到空间功率谱密度。根据国际标准化组织颁布的ISO 8608，路面不平度的拟合公式为

(9)

式中:Gq(n)是有效不平度空间功率谱密度，是由有效不平度时间功率谱密度PSD(f)进行双对数运算得出，单位为m3；n为空间频率，是波长λ的倒数，单位为m-1;n0为空间参考频率，取值为0.1 m-1；Gq(n0)是在n0空间频率下的功率谱密度值，单位为m3;w为频率指数。国际标准化组织颁布的ISO 8608文件中,按路面功率谱密度把路面的不平度程度分为8个等级，并规定了路面不平系数Gq(n0)的几何平均值，如表3所示。

表3 路面不平度8级分类标准Tab.3 8-Grade classification standard of road roughness

2 结果与讨论

本文以牵引车为动力带动振动测试台架进行测试。根据ISO5008可知，农用车辆在田间行驶时速度过慢会难以引起激励，速度太快造成非线性现象[21]。所以，在测试过程中为了保证能够引起测试台架的振动，将车速保持在2 km/h[22]。通过改变原始路面矩形坑的尺寸来改变路面的波长，采样频率设置为2 000 Hz。

2.1 有效不平度模型分析

运用Matlab编写m语言对深度10 cm，跨度为10 cm的数据进行运算，得出软路面有效不平度的时域功率谱密度(其余20组规律一致)。并对有效不平度的功率谱密度进行双对数求解，得出空间域谱图，如图5(a)所示，横轴为空间频率，纵轴为位移功率谱密度值，数据显示部分为0.1～1 000 m-1。可以看出，功率谱密度幅值在整个空间频率范围内变化较大，低频(长波)功率高于高频(短波)功率，且曲线随着空间频率值共分为三段，分别为0.1～1 m-1、1～10 m-1、10～1 000 m-1。在0.1～1 m-1段处于上升阶段，是由于此频带内路面较为平坦，产生的激励较弱。随着空间频率的升高，产生的激励增强。在空间频率1 m-1附近，功率谱密度值达到最高点，并开始下降，路面特性近似于文献[23-24]中的比利时路段。在1～10 m-1段功率谱密度曲线幅值较高，频率分布较为稀疏。在10～1 000 m-1频率分布较密，功率谱密度值较小，是由于土壤软路面极易变形且较短的波长对车轮的激励频率较高，同时难以造成较高的振动幅值所致。说明，车辆行驶在软路面上时，产生振动较大的波段主要在0.1～1 m(1～10 m-1)，短波产生的振动分量较小。所以在10～1 000 m-1范围内舍去不予以计算，如图5(b)所示。并可以看出功率谱曲线中均匀分布5个峰值点。

(a) 整体有效不平度功率谱密度

(b) 局部有效不平度功率谱密度图5 有效不平度功率谱密度时域、空间域图Fig.5 Time domain and spatial domain diagrams of effective roughness power spectral density

当路面不平度空间频率为n，车辆行驶速度为u(t)时，路面不平度输入时间频率f与路面不平度空间频率n之间的关系式为

f=u(t)×n

(10)

式中:n为空间频率，是波长λ的倒数，单位为m-1;u(t)为车辆行驶速度，即2 km/h。设矩形坑后端为主要的激励点，则路面激励的波长可以定义为两坑之间的间距与矩形坑跨度的和。本次试验包含21种矩形坑路面，共有7个波长。由于构造的矩形坑路面近似于非正弦周期信号，会有倍频现象[25-26]。又由于有效不平度空间功率谱密度中有5个峰值点出现，所以结合式(10)对原始路面不平度激励信号进行五次倍频统计，结合不同波长对应的空间频率n，时间频率f，如表4所示。

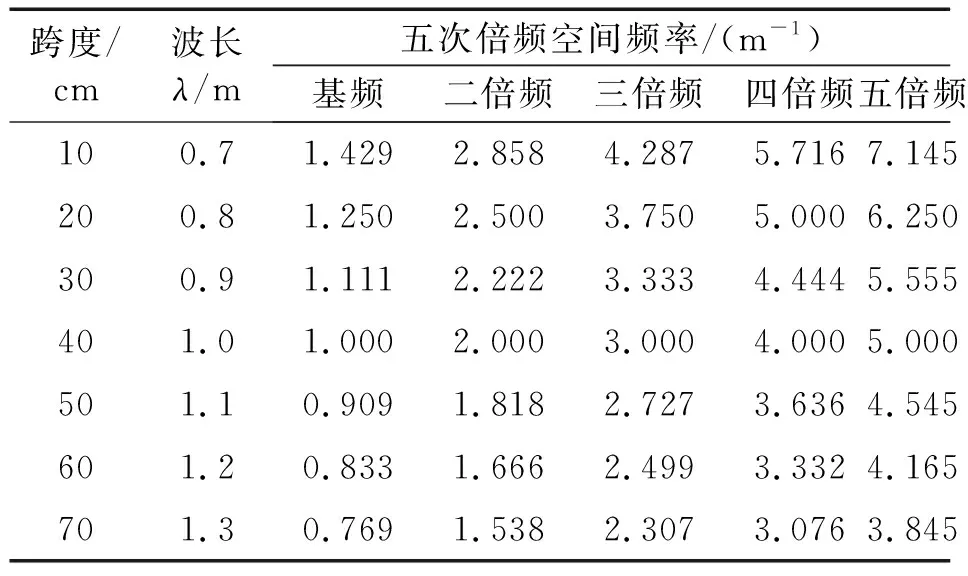
表4 原始路面不平度信号激励点波长、空间频率倍频统计Tab.4 Wavelength and spatial frequency multiplier statistics of the excitation point of the original pavement roughness signal

对有效不平度空间功率谱密度信号的峰值点频率与原始路面不平度的激励点频率的5次倍频进行线性回归分析。结果显示，有效不平度模型信号与原始路面不平度激励点频率的线性回归方程系数均接近于1，R2值范围在0.973 5～0.995 6，如表5所示。说明该路面的激励频率以及激励倍频与模型求解的有效不平度峰值点频率高度相关，与文献[27]中规律一致。表明有效不平度求解方法的有效性，验证了车辆在软路面上行驶时产生的激励点为矩形坑后端。

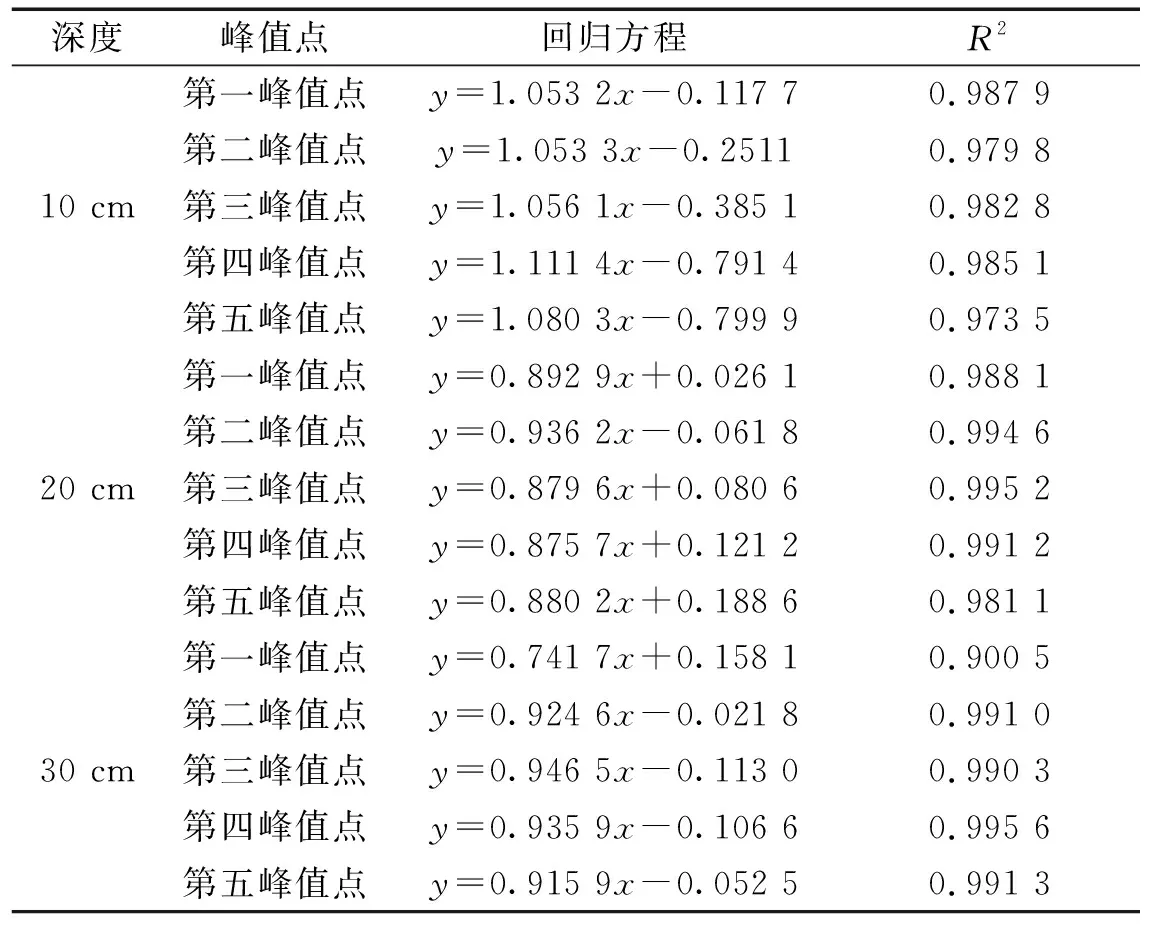
表5 有效不平度功率谱密度信号峰值点频率与原始路面不平度激励点的5次倍频回归分析统计Tab.5 Five times frequency regression analysis statistics of the peak point frequency of the effective roughness power spectral density signal and the original road roughness excitation point

将实际测得的有效不平度空间功率谱密度曲线峰值点频率与原始路面不平度矩形坑后端激励点的5次倍频进行分析，如图6所示。可以看出两者差值较小，且随着矩形坑深度的改变，有效不平度激励频率值和原始路面不平度激励频率值变化不显著；随着矩形坑跨度的增加，有效不平度激励频率值和原始路面不平度激励频率值降低。说明，矩形坑跨度的改变是改变路面波长的主要原因，间接改变有效不平度激励频率值。同时，有效不平度激励点频率略低于原始路面激励点频率。主要分为两个原因：① 在人工构造路面时的系统误差;② 在测试过程中，轮胎和土壤会产生变形增加原始路面的波长，导致有效不平度激励频率(与振动频率一致)与原始路面不平度激励频率值相比偏小。

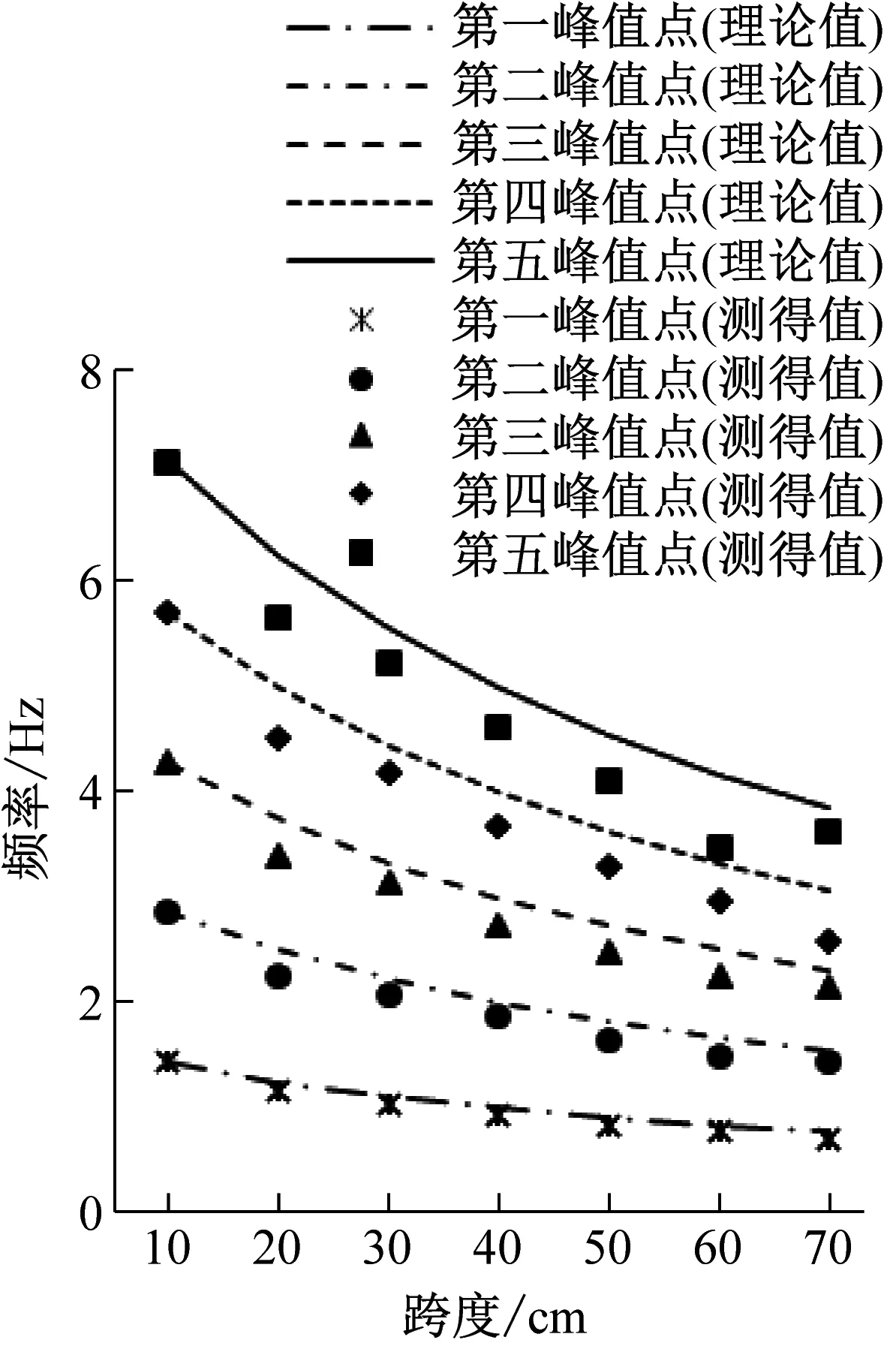
(a) 深度10 cm

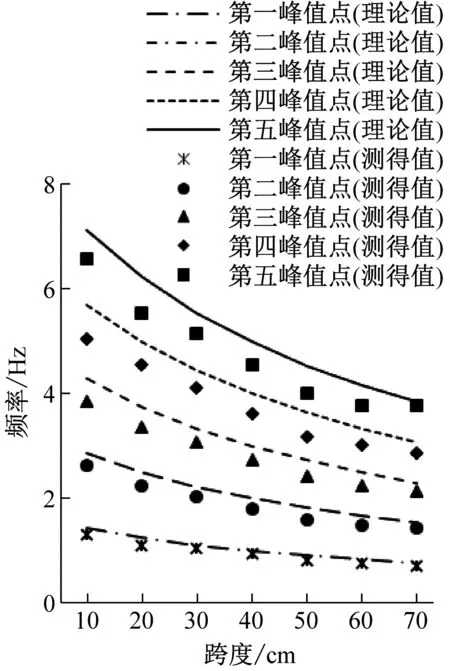
(b) 深度20 cm

(c) 深度30 cm图6 相同条件下原始路面不平度激励点5次倍频频率值和实际测量的有效不平度功率谱密度峰值点频率值Fig.6 5 times frequency value of the original road roughness excitation point and the frequency value of the peak point of the actual measured effective roughness power spectral density under the same conditions

2.2 路面等级特性分析

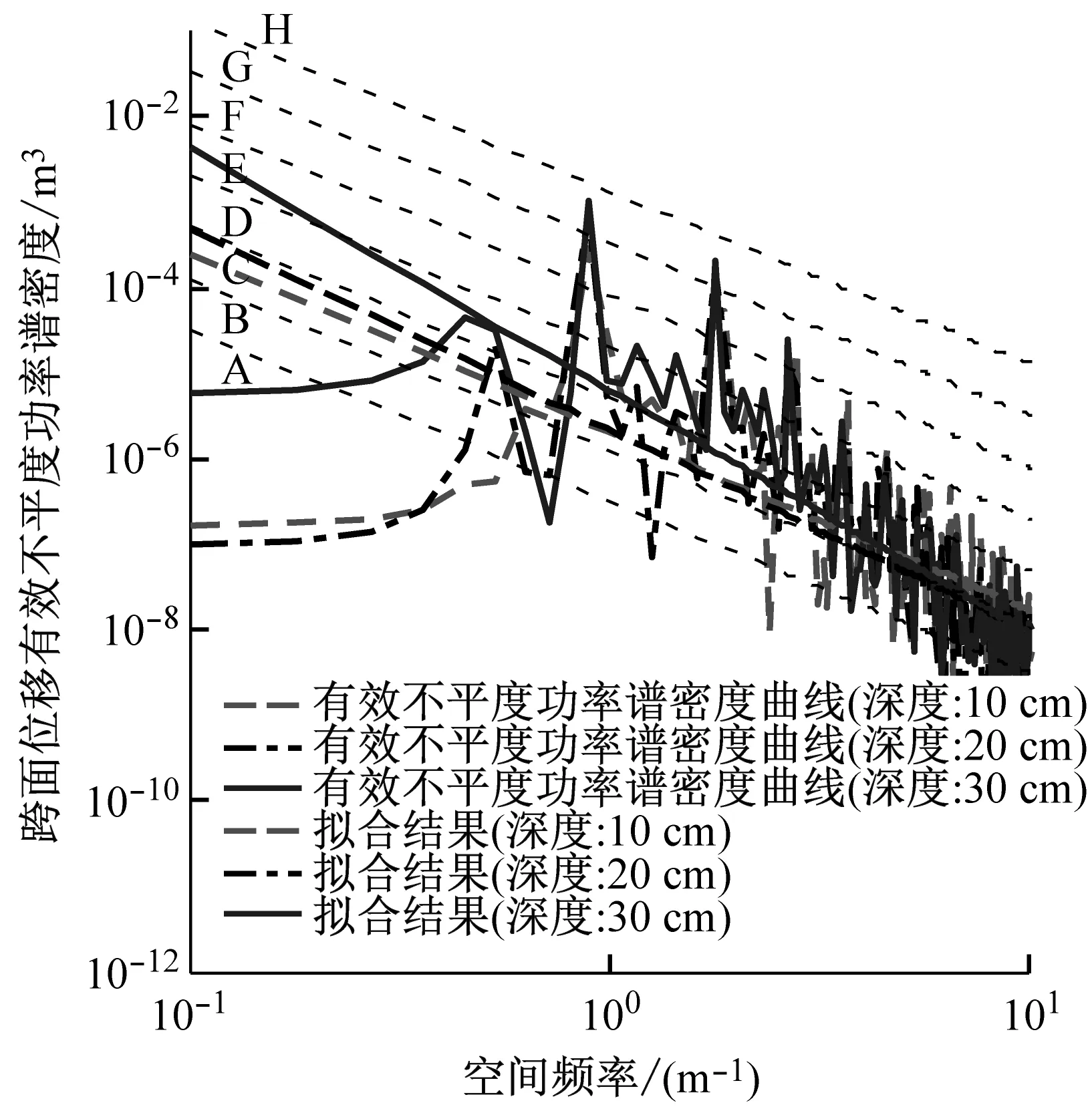
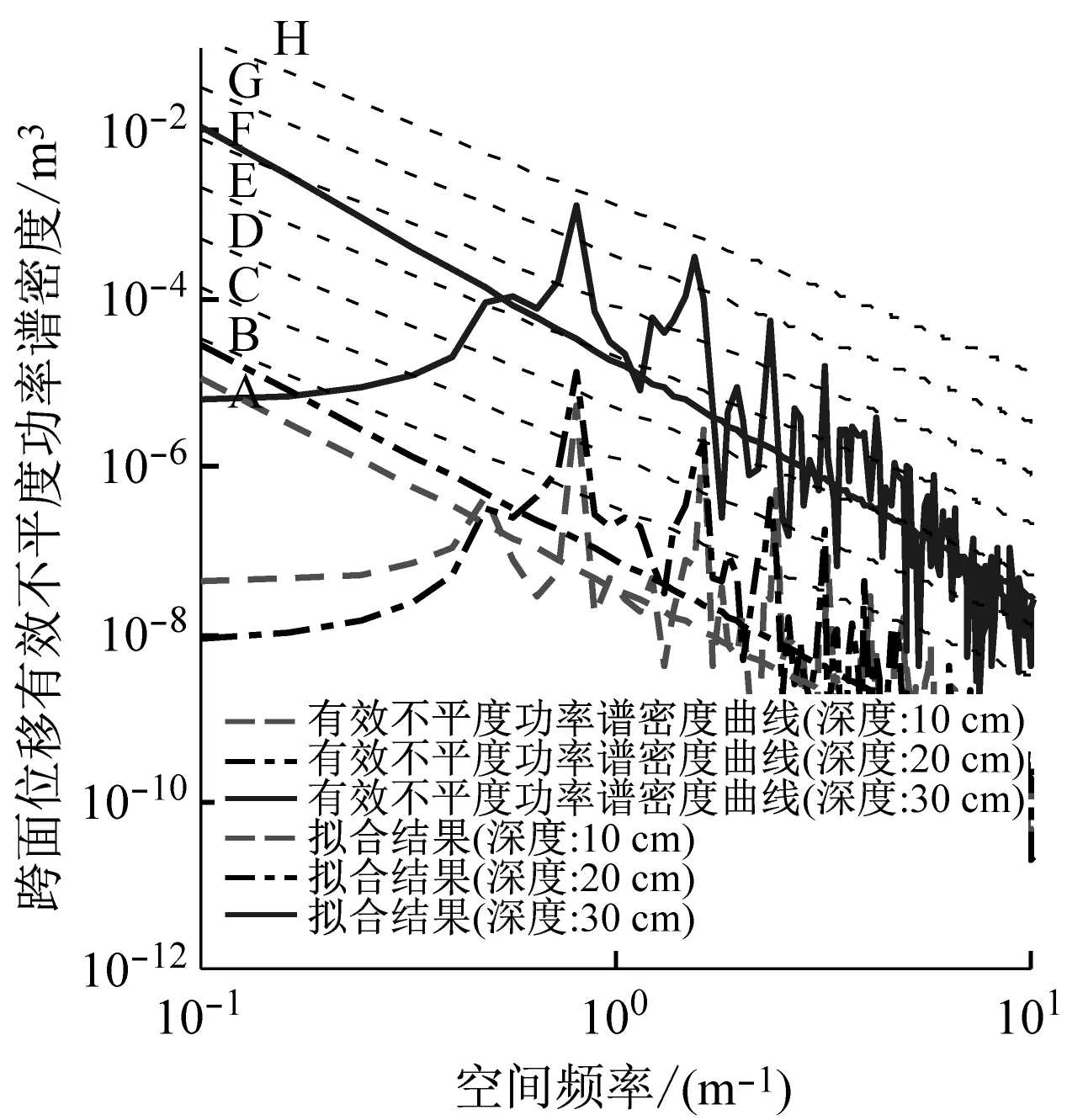
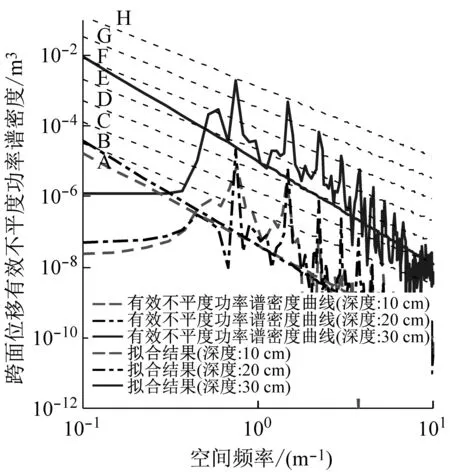
如图7所示，将21组试验数据以跨度为单位，将三个深度的矩形坑信息作为一组进行分析，共分为7组。其中，斜虚线是根据ISO 8608国际标准划分的路面不平度分级线，表示A～H级路面不平度功率谱密度范围，频率指数w取2。曲线为所测土壤矩形坑路面的有效不平度功率谱密度。结合式(9)以空间频率0.1 m-1处作为起点，以10 m-1为终点对功率谱密度曲线进行拟合。可以看出，在深度10～20 cm，跨度在50 cm、60 cm、70 cm时振动幅值较小，原因是矩形坑前端在车轮经过时坍塌过快，同时车轮会接触矩形坑底部，坍塌的松软土壤落在矩形坑底部会作为缓冲，以及矩形坑后端无法直接给与激励，导致该过程无法产生较大的激励。

(a) 跨度：10 cm

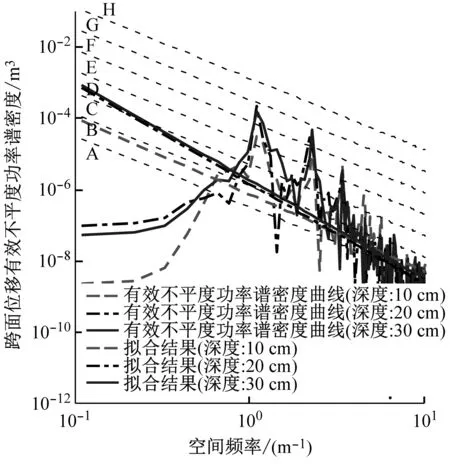
(b) 跨度：20 cm

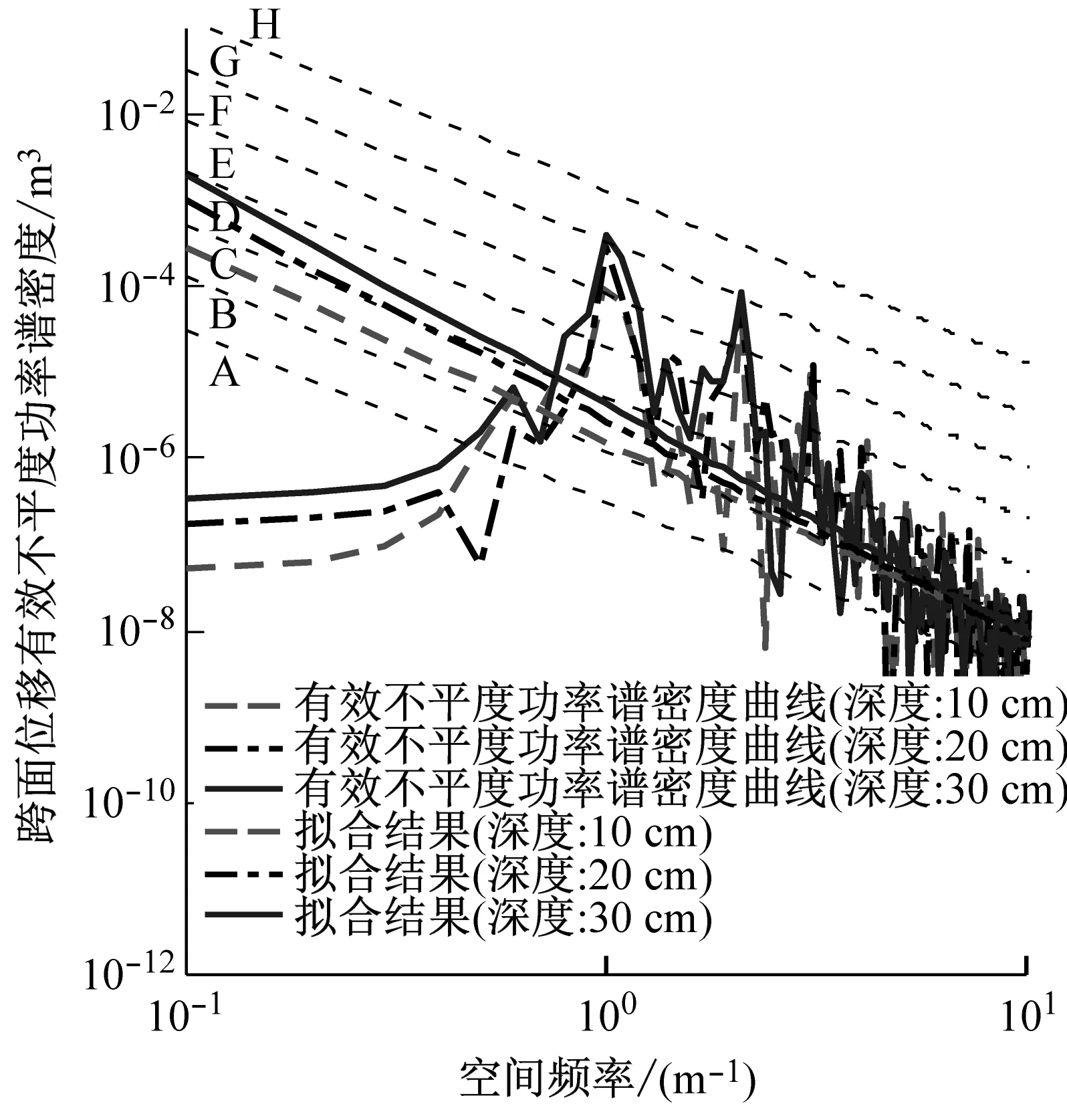
(c) 跨度：30 cm

(d) 跨度：40 cm

(e) 跨度：50 cm

(f) 跨度：60 cm

(g) 跨度：70 cm图7 21组土壤矩形坑路面有效不平度分级图Fig.7 Grad diagram of effective roughness of rectangular pit pavement in 21 groups of soil

继续对软路面的有效不平度频率指数w，拟合直线在空间频率0.1 m-1的功率谱密度值(路面不平度系数Gq(n0)值)进行统计，如表6所示。可以看出,采用对路面有效不平度功率谱密度曲线拟合的方法，可以对该路面进行较好的分级。随着跨度和深度的增加频率指数w在-2.944～-1.946，并且在21组数据中有一处大于-2，其余均小于-2，说明长波在软路面谱中分布较广，也是引起车辆振动的主要原因。同时，在测试轮未接触矩形坑底部的功率谱密度中，随着矩形坑跨度(波长)的增加，峰值点的幅值增大，说明在接触矩形坑后端时产生的瞬间激励较大，与驾驶员的主观判断一致，表明测试和求解的精度较高。路面等级随着矩形坑跨度的增加先增高后降低，最高到达F级，拟合直线最高可穿过3个路面等级。因为矩形坑跨度增加，导致路面长度增加，且有效激励次数不变，所以平均功率值降低。说明单一瞬间激励的强弱无法决定整体路面等级。

表6 路面等级参数统计Tab.6 Pavement grade parameter statistics

3 结 论

本文针对田间长波路面设计了一套有效不平度测量装置，并运用矩形坑路面模拟土壤软路面中不同的波长，并建立车辆—软路面有效不平度模型，以此探究田间软路面长波的有效不平度激励特性。

对21种不同路面的有效不平度曲线进行分析，峰值点对应的空间频率随着跨度的增加而降低，与矩形坑后端作为激励点频率的相关系数(R2)范围在0.973 5～0.995 6。说明产生激励的点主要为矩形坑后端，并验证了求解田间长波路面有效不平度方法的有效性，为土壤软路面谱的测量提供了新方法。

通过田间路面的有效不平度时域功率谱密度和空间功率谱密度的分布规律可以看出，整体数据波动较大，并分为规则的三段数据，幅值较高段为1～10 m-1；21种路面的频率指数w得范围在-2.944～-1.946，且有20种路面的值均小于-2。随着波长增加路面等级先升高后降低，峰值点幅值升高。说明长波路面在路面谱中分量较大，也是引起车辆振动的主要原因；同时表明土壤软路面的分级方式符合ISO国际标准，也符合驾驶员的主观评价。为土壤软路面谱的建立提供新的依据。

本文以固定车速和构造的21种田间路面为出发点结合振动响应反馈位移激励的方法，讨论了田间长波路面的有效不平度和分级特征。为下一步在不同车速下对不同农机具耕作的田间路面的探究做了铺垫工作。