1种改进的流变模型在层状覆盖层坝基上的应用*

王 璠，毛海涛,，侍克斌，王晓菊

(1.新疆农业大学 水利与土木工程学院，新疆 乌鲁木齐 830052；2.山西农业大学 城乡建设学院，山西 太原 030000)

0 引言

河谷中的第四纪松散沉积物主要成分为颗粒粒径较大的漂卵砾石、块碎石以及粉细砂等，粗粒土分布相对更加广泛，且呈强弱相间的层状分布，深度从几十米到几百米不等。在这类地基上建坝，地基承载力不足、稳定性难以满足要求、基础沉降和不均匀沉降过大等是常见问题。除了施工措施原因外，忽略整体覆盖层尤其是粗粒土层的流变性也是原因之一。

土石料的流变模型中主要有Maxwell模型[1]、Burgers模型[2]、Kelvin模型[3]、Bingham模型[4]、理想黏弹塑性体[5]、西原模型[6]等。这些模型通过基本元件的“串联”和“并联”来描述岩土介质的流变特性，建立岩土应力-变形-时间的本构模型，能反应岩土线性黏弹塑性性质，但不能表达岩土的加速蠕变特性；元件模型元件越多，模型越复杂，参数就越多，模型数值计算就越困难[7]。在以往研究岩土变形的流变模型中，H-K模型能较全面地反应岩土弹性、蠕变、松弛变形特性，如蔡新等[8]采用流变学理论，选取Maxwell模型和H-K模型模拟单一岩土料的流变特性，探讨土石料流变特性对土石坝应力、位移的影响；李习平等[9]采用非线性拟合方法，比较了H-K模型和Burgers模型的拟合值与实验数据的关系，验证了H-K模型研究地基流变的适用性；胡刚等[10]将空区顶板-矿柱体系简化为弹性矩形薄板H-K流变力学模型，来分析空区处理对围岩及地表的影响规律。但H-K模型对于单一岩土体的流变研究具有优势，而对性状各异的多层土模拟结果往往与实际有较大出入，覆盖层地基大多由多层岩土体组成，需要研究适合其变形的多层土流变模型。

综上，本文对H-K模型进行改进，研究新的计算模型以适应层状覆盖层的特点，并以青湾坝为例，采用Comsol建立层状覆盖层上大坝流变及流固耦合数值模型，结合实测数据以确定模型的准确性，进而全面评价层状覆盖层流变对坝体、坝基以及主要结构的影响，以期为深厚覆盖层上大坝的稳定计算提供支持。

1 层状覆盖层流变模型

1.1 单一土层的H-K模型

H-K模型从其元件构造上能直观地识别弹性和黏弹性变形分量，其数学表达式能客观地描述蠕变、应力松弛及稳定变形等。

该模型由1个弹模为E1的弹性元件(H)和Kelvin(K)体串联而成如图1(a)，其变形随时间的关系如图1(b)所示。在应力σ作用下，应力-应变关系如式(1)所示：

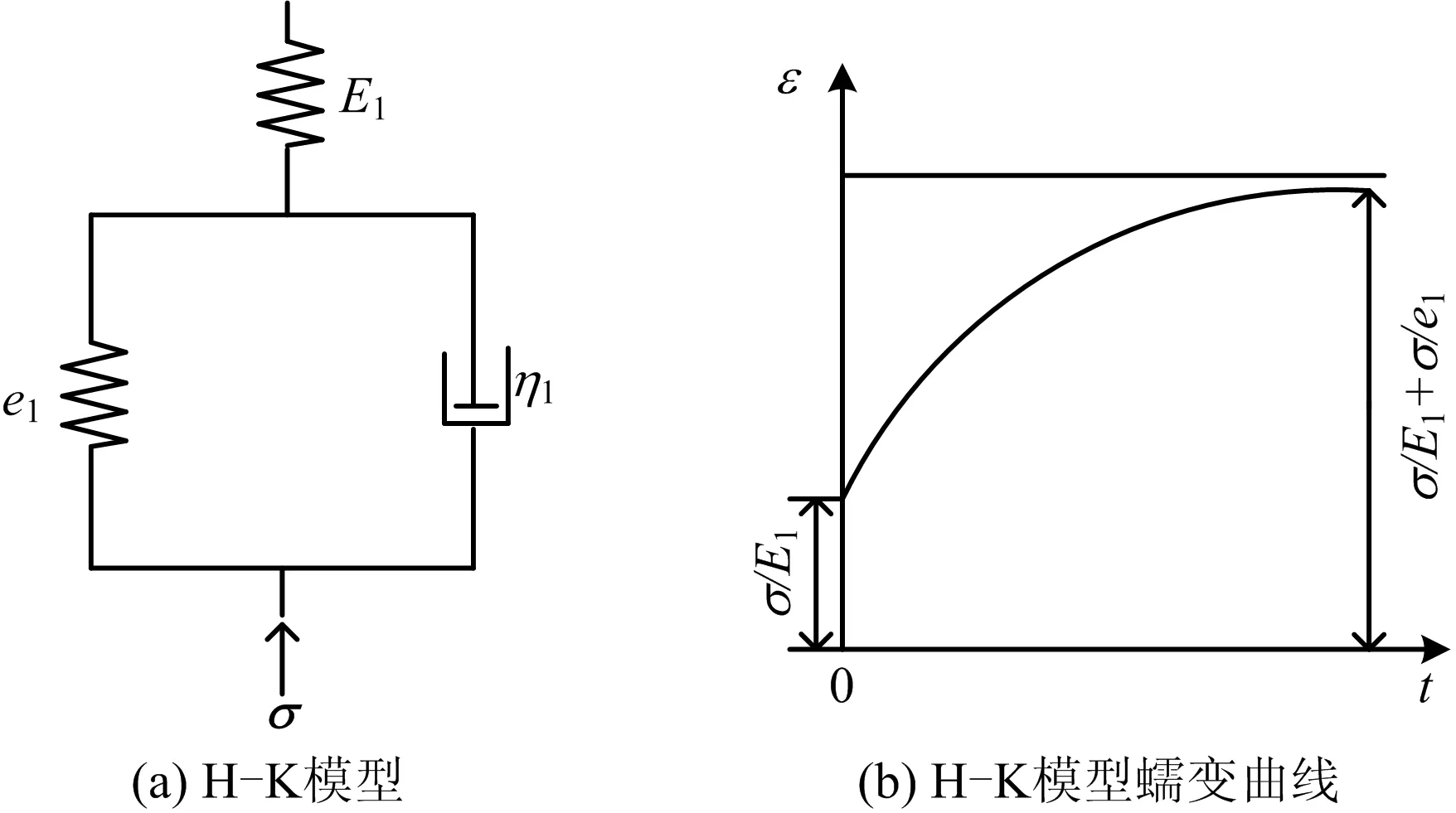
图1 H-K的蠕变模型Fig.1 H-K creep model

(1)

式中：E1，e1分别为H弹簧体及Kelvin 体的弹性模量，Pa；η1为Kelvin 体的黏性系数，m2·s-1；σ是应力，Pa；而总应变ε=εH+εK，其中εH，εK分别为H弹簧体及Kelvin体的应变。

1)当∂σ/∂t=0，即应力σ不随时间变化，由初始应变ε0=σ/E1可得，如式(2)所示：

(2)

由公式(2)可知，应变随时间持续递增(t→∞时，ε→σ/E1+σ/e1)，其应变速率由起始时的最大值逐渐趋近于零。

2)当∂ε/∂t=0，即应变ε不随时间变化，由初始应力σ0=E1ε可得，如式(3)所示：

(3)

由公式(3)可知，应力随时间增大而减小(t→∞时，σ→E1e1ε/(E1+e1))。

上述分析可知，H-K是时间上的衰减模型。模型中关键参数为E1，e1，η1，可通过室内外岩土体流变试验获得。此外，还与泊松比μ，渗透系数k等有关。对于层状覆盖层，各层岩土体特性差异较大，蠕变变形也各不相同，采用H-K模型不能较好反应覆盖层整体蠕变特性。

1.2 多层土H-KS模型的建立

在层状坝基中将每层土作为1个单元，考虑各层之间存在力的传递，各土层性质不同，因此，可将每层土视为1个H-K体，各层总体为串联关系如图2(a)所示。由H-K体串联得层状坝基模型如图2(b)。

由于模型元件构造复杂不利于分析计算，结合模型中各元件所代表的含义，将图2(b)中各层不随时间变化的弹性模量E1、E2、…，Ei合并为模型整体弹性模量E，关系如式(4)所示：

图2 多土层坝基串联模型Fig.2 Multi-soil dam foundation series model

(4)

式中：E为弹性模量，Pa；Ei对应各层岩土变形初期的弹性模量，Pa。

得到简化后的模型如图3，其中E为与时间因素无关的整体变形模量，各层与时间因素相关的蠕变模型不变化。

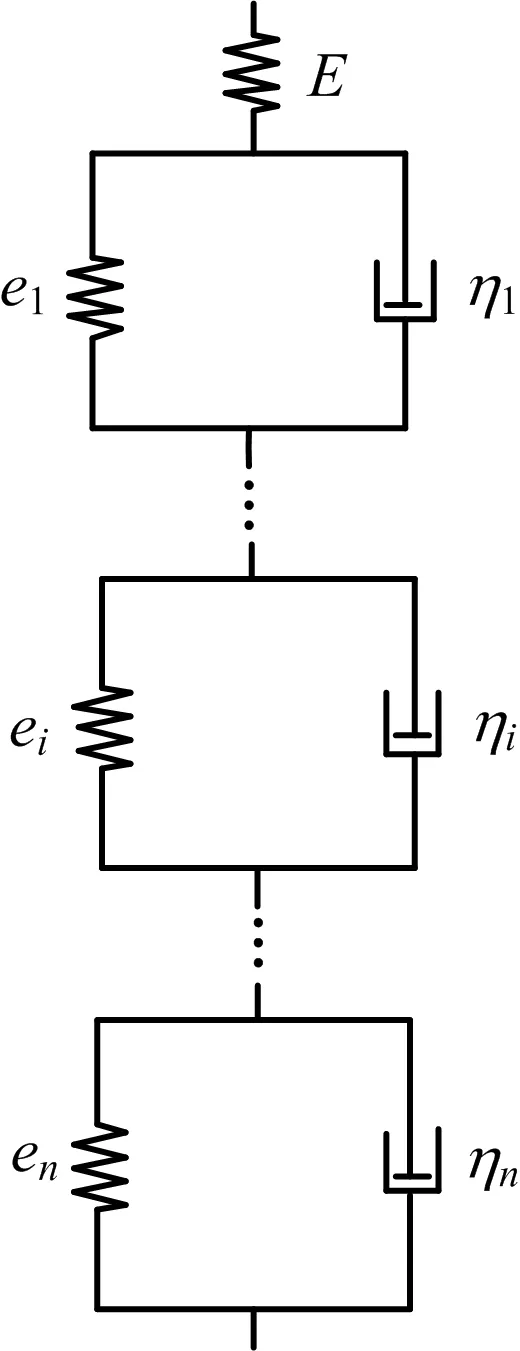
图3 简化后层状土层串联模型Fig.3 Simplified series model of layered soil

简化后形成层状坝基流变计算新模型(以下简称H-KS模型)，在通过试验获取参数方面，该模型因试验次数减少而降低了误差，提高了计算结果精度。

总应变εt等于各H-K元件的应变之和，表达如式(5)所示：

(5)

式中：ε1、ε2、…、εn分别为对应各层岩土的变形量，m。

将式(2)代入式(5)得方程，如式(6)所示：

(6)

式中：σ为恒定应力，Pa；t为加载时间，s；Ei对应各层岩土变形初期的弹性模量，Pa；ηi对应各层黏弹变形的黏滞系数，m2·s-1。

联立式(4)和式(6)可得到模型的变形方程，如式(7)所示：

(7)

式中：E为弹性模量，Pa。

坝基沉降除了受岩土体流变作用外，还受流固耦合效应的影响。因此，坝基沉降需要将流变与流固耦合模型联合计算。

2 流固耦合模型

2.1 渗流偏微分方程

描述多孔介质饱和流体流动的达西定律质量守恒建立流体的连续性方程[11]，如式(8)所示：

(8)

式中：ρ为液体密度，kg·m-3；u为达西速度，m/d；ε∂(ρεp)/∂t为多孔存储项，m/d；Qm为液体源汇项，m/d。

其中多孔存储项表达如式(9)所示：

(9)

式中：S为多孔介质存储系数；P为水头，m。

达西速度表达如式(10)所示：

(10)

式中：k为渗透率，md；μ为液体动力黏度，N·s·m-2；Pf为孔隙压力，Pa；g为重力加速度，m·s-2；D为位置水头，m。

Qm为液体源汇项，由于孔隙空间的膨胀率(∂εvol/∂t)增加，使液体的体积分数增加，从而引起液体汇，如式(11)所示：

(11)

式中：αB为Biot系数；εvol为多孔介质体应变。

将式(9)～(11)代入式(8)可由质量守恒方程得式如式(12)所示：

(12)

式中：H为总水头，m。

2.2 固体骨架变形方程

孔隙弹性将多孔介质中流体流动及颗粒变形联系起来，得到应力、应变和孔隙压力的本构关系，由Biot理论可得流体含量增量、体积应变和孔隙压力的本构关系[12]，联立如式(13)所示：

(13)

式中：σ是柯西应力张量，Pa；C为弹性矩阵；ε是应变张量；αB是Biot系数；Pf是流体孔隙压力，Pa；I为单位矩阵；ζ为多孔介质中流体含量的变化值，m3。

固体颗粒的体积变化Pm的表达式如式(14)所示：

Pm=-Ksεvol+αBPf

(14)

式中：Ks为固体的弹性模量，Pa。

2.3 耦合的实现

采用COMSOL多场耦合来实现流固耦合，其具体流程如图4所示。该流程能完成某一时刻的数值模拟，下一个时刻，应力张量可作为1个附加的各项同性项参与计算[13]，并视为下一时刻的1个初始应力，则该时刻总的初始应力为Pt1，其表达如式(15)所示：

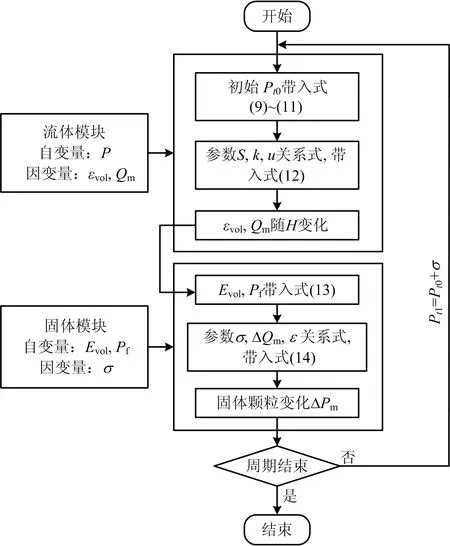
图4 坝基沉降过程数值模拟流程Fig.4 Numerical simulation procedure of dam foundation settlement process

Pt1=Pt0+σ

(15)

式中：Pt1、Pt0分别为t1及t0时刻的初始应力，Pa；σ为t0时刻计算的应力张量，Pa。

整个耦合过程在每一个时间段内反复迭代求解，直到沉降完成为止。

此外，为了解坝基各层流变对其应力应变及渗流的影响，将常用的非流变模型—分层总和法结合流固耦合模型(以下简称HSM模型)与本模型计算结果进行对比分析。

3 工程应用

3.1 工程概况

青湾均质土坝最大坝高50 m，坝长200 m，水库正常蓄水高度45 m。上下游坡度均为1∶2。坝基覆盖层约80 m，根据颗粒组成及物理力学性质等差异，可将其自下而上分为5层：1)以粗粒为主的冰水积含漂卵砾石层，厚11.5 m；2)以细粒为主的堰塞堆积粉细砂层，厚13 m；3)以粗粒为主的冲积含漂砂卵砾石层，厚17 m；4)以细粒为主的堰塞堆积粉细砂层，厚15 m；5)以中粗粒为主的冲洪堆积含漂砂卵砾石层，厚25 m。覆盖层各土层的物理力学参数见表1。

表1 坝体及各层岩土物理力学属性Table 1 Physical and mechanical properties of dam body and each layer of rock and soil

3.2 建模计算

在Comsol中通过自动划分网格，得到1 086个域单元，239个边界元，求解自由度为7 069个，具体见图5。模型底部和两侧设置为固定约束且为不透水边界；上游侧为透水边界，大坝上下游水位分别为45 m和0 m，淹没在水位以下的上游河谷及坝面设置为总水头边界，其它边界设置为潜在出渗边界。

图5 大坝数值模型网格剖分单元Fig.5 Grid division unit of dam numerical model

为了监测坝基沉降、应力和渗流等相关指标，大坝设置了完整的监测系统。为监测坝基沉降，在基建面及截水槽底部共设置5组水管式沉降仪；坝体位移监测包括水平和沉降2项，分别在坝底面、高度为20 m和35 m水平面安装沉降和水平位移设备；在渗流监测方面，坝体内部设置测压管并在坝后设置量水堰。此外，还在坝轴线(断面2)、截水槽底部等重要部位设置应变及渗压计等，大坝监测点布置如图6。

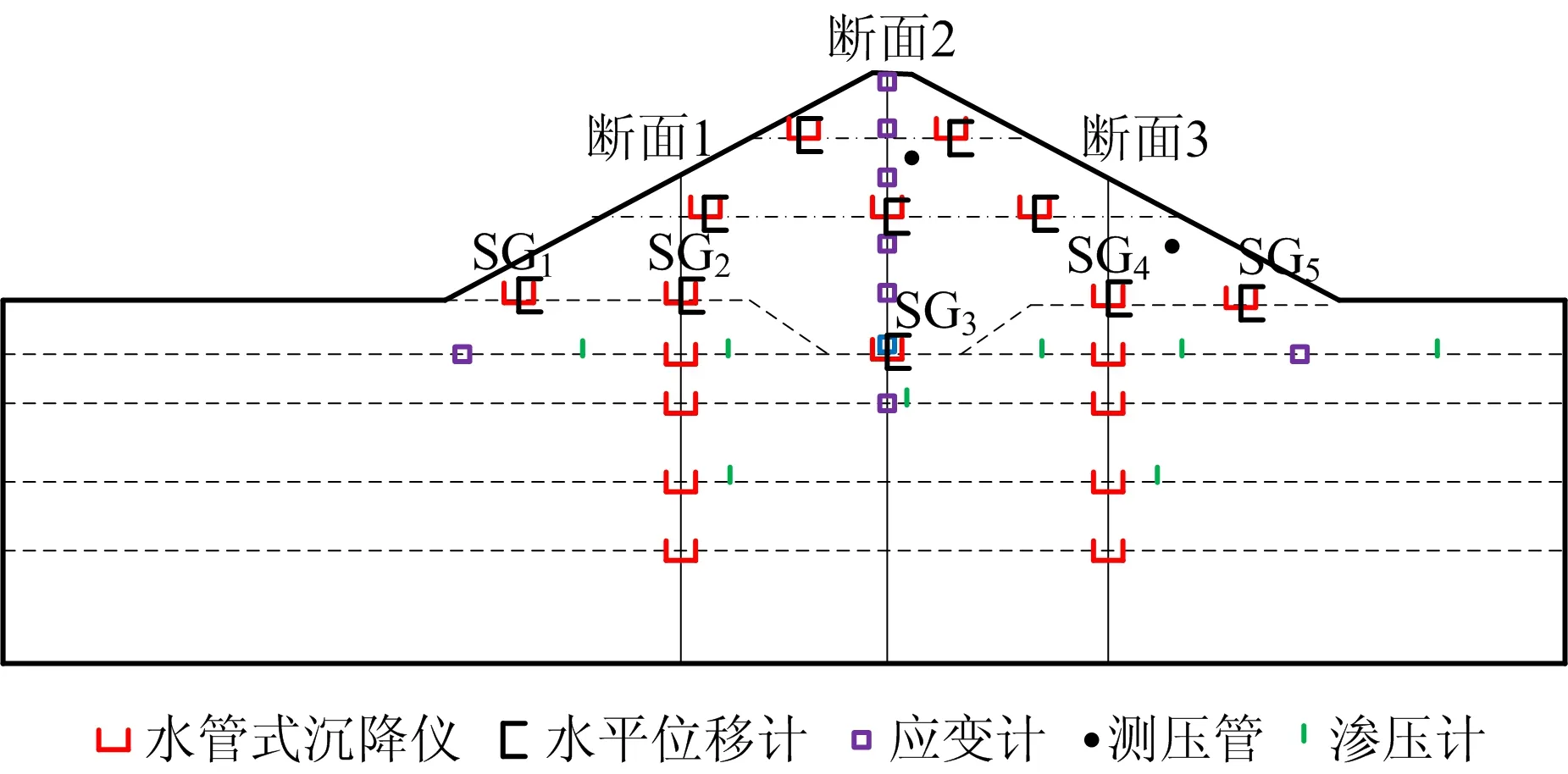
图6 坝体监测系统布置Fig.6 Layout of dam monitoring system

4 结果分析

4.1 大坝沉降分析

4.1.1 覆盖层各土层沉降

采用HSM及H-KS模型分别对大坝沉降进行计算，其结果如图7所示。

图7 2种工况下沉降等直线Fig.7 Contour lines of settlement under two working conditions

由图7可知，H-KS模型计算的沉降量总体上高于前者。坝基各土层的变形增量自上至下分别为11.3，2.5，17.8，4.3，22.5 mm。对比发现，以粗粒土为主的1)，2)，3)土层沉降增量较大，占总沉降量的88.4%，单位厚度增量分别为1.0，1.1，0.9 mm/m。其中5)层厚度较大且位于底部，其变形总量也相应较大，占总增量的38.5%；细粒土为主的土层2)，4)总体变形较小，沉降单位厚度增量仅为0.2，0.3 mm/m。由此可见，考虑流变后的沉降不仅与各土层的性质有关，还与其厚度及所在位置相关。

4.1.2 结果验证

为验证计算结果的准确性，结合图6中坝基沉降监测数据对比结果如表2所示，并以断面1位置为例绘制对比图如图8。

表2 坝基各层沉降量对比Table 2 Comparison on settlement of each layer of dam foundation mm

图8 大坝监测断面1处沉降对比Fig.8 Comparison on settlement of dam monitoring section 1

由表2和图8可知，H-KS模型计算的沉降量在各土层及整体上均与实测值更接近，而HSM模型计算结果与实测值误差较大。说明H-KS模型计算结果与实际沉降更吻合。对于该粗细相间的层状坝基，各层土的沉降量在2种算法下也不尽相同。其中，HSM模型在1)，3)，5)粗粒土层中计算误差较大，如SG1处误差分别为27%，10.6%，16.1%；而细粒土层2)，4)计算结果误差相对较小，误差仅为为0.89%和2.6%；此外，H-KS模型在各土层的沉降计算误差均在5%以内。

综上，HSM模型在流变性较小的细粒土沉降计算中基本符合实际，但在粗粒土层坝基沉降计算方面与实际有较大出入，而考虑流变的H-KS模型计算结果与实际沉降基本吻合。

4.2 应力分析

坝基岩土流变对大坝整体强度会有一定影响，尤其是粗细相间的层状坝基，各土层流变对大坝应力的影响尚不明确，需要进一步探索。

4.2.1 应力整体分布

2种模型下的大坝应力分布如图9所示。

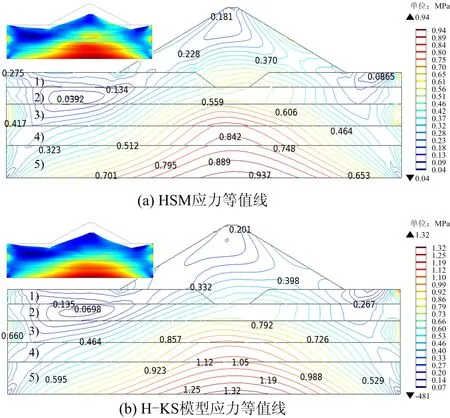
图9 应力分布等值线Fig.9 Contour lines of stress distribution

由图9可知，H-KS模型计算总体应力水平高于前者，坝体和坝基应力分布均是自上而下逐渐增大，并在坝基底部出现应力极值，分别为0.937，1.32 MPa。受坝基流变的影响，坝体整体应力水平有所增长，但增量率较小。值得注意的是，坝踵和坝趾处的应力均有明显增大，增量达到0.027，0.03 MPa。

4.2.2 覆盖层各土层应力变化

取坝轴线处各层应力计算结果如图10，需要说明的是，由于坝轴线处的截水槽将1)层全部替换，替换后土料和均质土坝一致，为细粒黏性土，因此该处计算结果不反应原来的粗粒土。

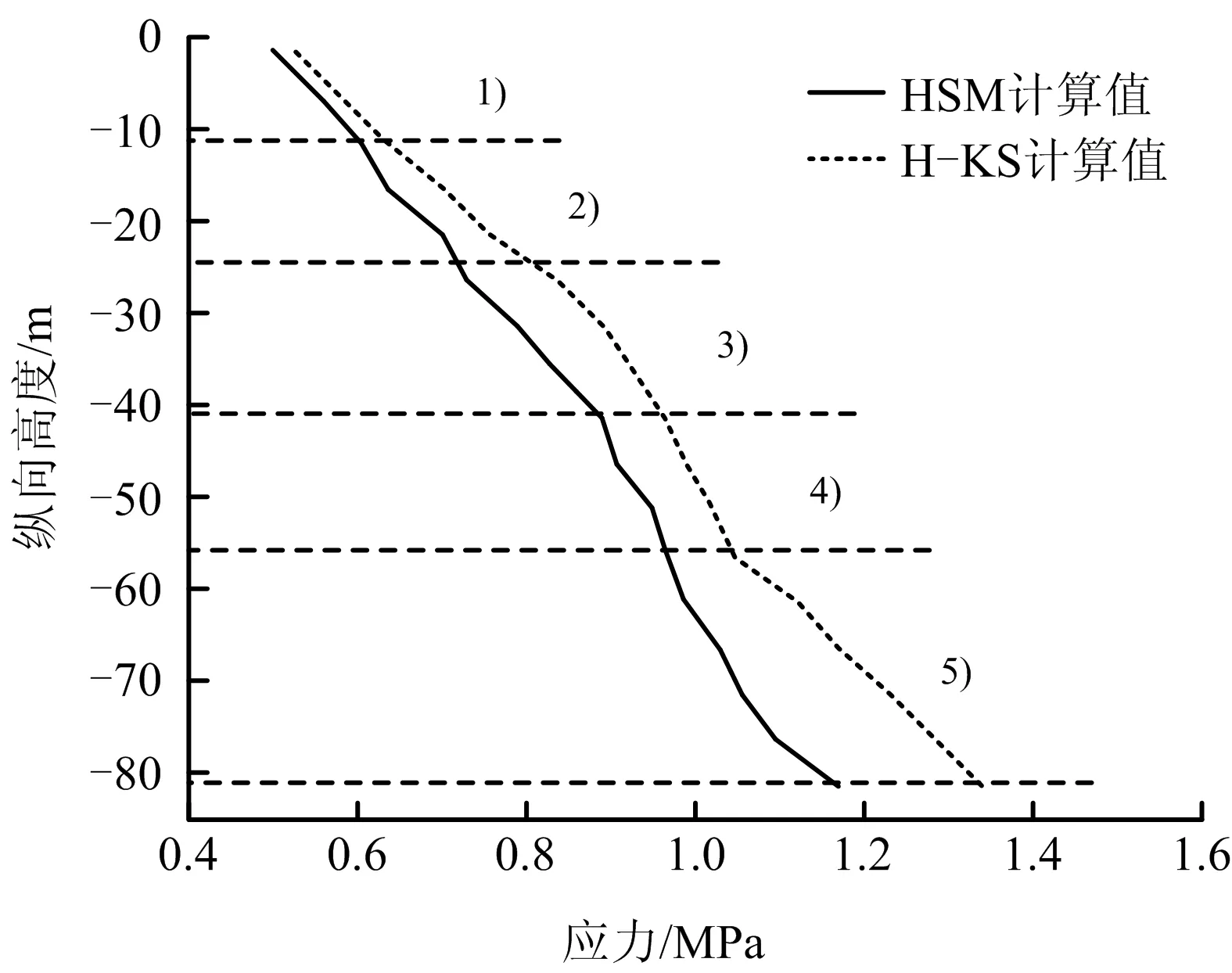
图10 坝轴线处覆盖层各层应力变化Fig.10 Change in stress of each layer of overburden at dam axis

由图10对比发现，以粗粒土为主的3)，5)层应力增量明显高于以细粒土为主的1)，2)，4)层。自上而下各层的应力增量分别约为0.03，0.06，0.1，0.07，0.17 MPa。其中，性质单一、颗粒最细的1)层(截水槽处)应力差别最小，误差在1.2%，2)，4)土层应力增长也较小，均在5.75%左右；而5)层差别最大，总体应力水平增长率约为15.2%。可见，在流变性大的粗粒土层应力方面增量也较大，而在流变性较小的细粒土层应力增量相对较小，说明土层流变性影响着应力变化。

4.2.3 应力结果验证

结合坝体监测数据，取图6中坝体中坝轴线位置应力监测值与2种模型计算结果进行对比如图11所示。

图11 坝轴线处坝体应力变化Fig.11 Change in stress of dam body at dam axis

由图11可知，坝轴线处坝体应力自上而下变化规律不同，自坝顶向下16m应力值随高度基本无变化，甚至出现变小趋势，本模型应力值与实测值吻合且大于HSM模型计算结果；16～26 m处应力与高度呈非线性变化，应力由0.18 MPa增至0.23 MPa，2模型计算结果均与实测值能较好吻合；26 m至坝底应力与高度基本呈线性变化，拟合线性关系分别为：y=-91.1x+43.7、y=-74.8x+40.2，HSM随着高度下降，偏差逐渐加大，H-KS模型计算结果与监测值基本一致。因此，本模型的正确性得到验证，相对于传统模型优势显著。

4.3 坝体变形和应力变化原因分析

综合4.1～4.2计算结果，将2种模型得到的坝体应力、变形极值对比如表3。

表3 坝体应力变形极值对比Table 3 Comparison on extreme values of dam stress and deformation

H-KS模型坝体最大沉降较前者增大15.7%，最大应力值也增大10%。分析其原因，主要是覆盖层各层持续的流变变形对坝体产生的影响。岩土体变形可分为2个阶段：外力变形阶段和流变变形阶段。其中，外力变形阶段大坝在施工碾压过程中，主要受到上部碾压作用压迫，颗粒棱角逐渐破碎、发生位移，孔隙被填充和压密。这一过程随外力碾压功的增加，坝基料孔隙逐渐压密，但上部碾压功影响有限，本阶段岩土料变形并没有彻底完成，大坝填筑完成后，压缩也基本结束。流变变形阶段的施工外力影响完毕，该阶段变形主要是在自重及水荷载作用下的进一步变形，颗粒之间孔隙逐渐减小并密实，这是一个随时间推移变形逐渐趋于稳定的过程。显然，坝体的变形受到坝基覆盖层变形的影响，传统的HSM模型仅计算了外力变形阶段，忽略了流变变形阶段，故而坝体变形相对较小，这与实际情况是不相符的。H-KS模型计算结果相对偏大，但更加符合实际坝体的变形情况。

4.4 渗流分析

除了上述应力场的变化，覆盖层中岩土体流变也影响着渗流场的改变，也是1个流固耦合过程。

4.4.1 大坝孔隙水压力分布

分别计算HSM、H-KS模型得到大坝孔隙压力分布如图12所示。

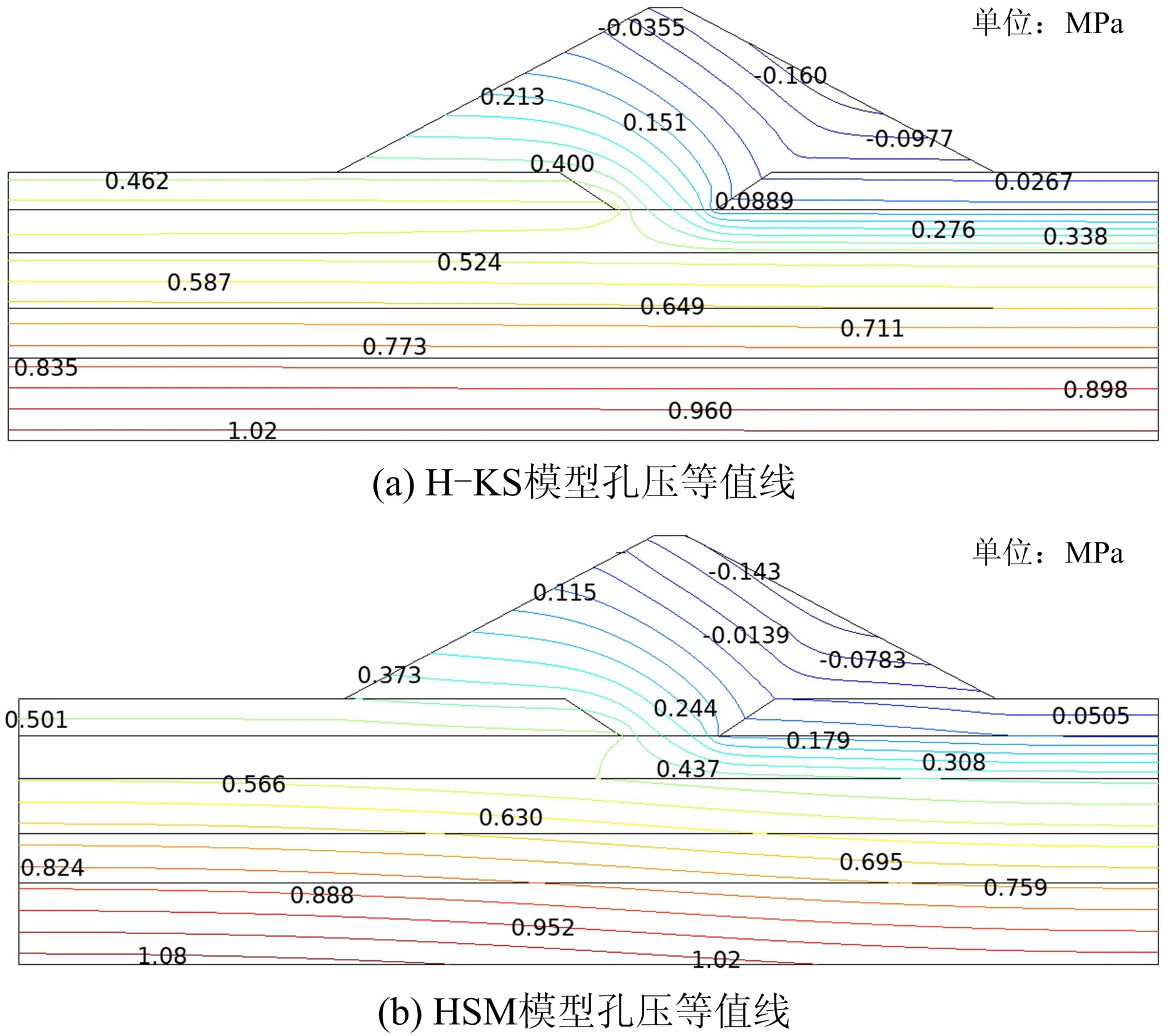
图12 孔隙水压力等值线Fig.12 Contour lines of pore water pressure

由图12可知，H-KS模型计算的各层土体孔压均小于前者，其中流变性大的粗粒层1)，3)，5)孔压减小量较大，平均减小量分别为0.039 MPa，0.043 MPa，0.06 MPa；而流变性较小的细粒料层2)，4)孔压减小量相对较小，仅为0.013 MPa和0.015 MPa。可见岩土体流变对粗细土层的影响也不同，以5)，2)层为例，前者减小约50.6%，而后者仅减小2.48%。分析其原因，主要是各层土在流变效应下，土骨架被压缩而孔隙体积减小，使原来由孔隙水承担的部分压力转由土骨架承担，孔隙水压力减小。其中，粗粒土相对细粒土流变性较大，其孔隙水压力减小量也更大。显然，颗粒孔隙体积的变化加速了流固耦合过程，使坝基渗流场与应力场趋于稳定的时间变短。

4.4.2 渗流结果验证

大坝渗流量实测结果与2模型计算结果对比如表4所示。

表4 坝后渗流总量对比Table 4 Comparison of total seepage amount behind dam

由表4可知，渗流稳定后采用HSM模型计算的渗流量比实测值增加了0.08 m3/s，增量为21.6%；采用H-KS模型计算的渗流量比实测值减少了0.03 m3/s，减小率为8.1%，与实测结果更吻合。

5 讨论

5.1 深厚覆盖层考虑流变的重要性

研究表明[14]，我国西南山区河谷覆盖层自下而上分为1)含泥砂卵碎石层(Ⅰ)；2)漂卵石、含泥砂碎块石、粉细砂互层(Ⅱ)；3)现代河流漂卵石层(Ⅲ)共3大层，覆盖层中粗粒含量相对细粒占比要大得多。本文反映了由于粗粒土流变性较大[15]，大坝运行后其变形、应力、渗透性等变化主要受到粗粒土流变的影响。常规计算方法忽略了覆盖层流变尤其是粗粒土流变的影响，结果与实际情况不相符。忽略覆盖层流变会导致土石坝沉降等变形超过预期，坝体内部因不均匀沉降出现裂缝、结构脱落甚至破坏，影响坝体的安全稳定。深厚覆盖层上大坝的出险加固难度相对较大，前期的设计和坝基处理若未考虑其流变性，也会为后期留下隐患。因此，在深厚覆盖层上建坝，科学对待坝基的流变性并采取合理的工程措施是至关重要的。

5.2 流变对流固耦合的影响

计算结果表明，考虑坝基流变相比不考虑流变模型的沉降量增加了约75 mm，也就是说考虑了坝基流变性后，岩土体的实际孔隙压缩较快且会更小，其渗透性更加弱化，增强了坝基的渗透稳定性。若不考虑流变，流固耦合过程和时间会更长，最终结果也有一定偏差。所以说，流变加速了流固耦合，缩短了流固耦合时间，渗流计算结果更加符合实际情况，为渗流控制与分析提供更合理的理论支持。

6 结论

1)对于岩性、物理力学性质差异较大的层状覆盖层坝基，采用H-KS流变模型能较好反应大坝应力、变形和渗流实际情况，与监测值对比，误差在5%以内，模型在模拟层状坝基方面具有明显的优势。

2)H-KS模型计算结果相比不考虑流变模型的应力、变形分别增大了10%和15.7%，部分增量会影响到大坝结构的安全稳定，应予以重视。

3)流变会导致大坝整体渗透性降低，粗细粒层孔隙水压力分别减小了约50%和2.5%，加速了流固耦合过程，对于重新评估大坝的渗透性有重要参考意义。

4)由于流变性不同，深厚覆盖层中粗粒土层对变形、应力和渗流方面影响最大，细粒土的贡献相对较小；除了与岩性相关之外，还与土层所处位置、厚度等相关。