基于随机搜索优化XGBoost的瓦斯涌出量预测模型*

马 恒，任美学，高 科

(1.辽宁工程技术大学 安全科学与工程学院，辽宁 葫芦岛 125105；2.矿山热动力灾害与防治教育部重点实验室，辽宁 葫芦岛 125105)

0 引言

为有效降低瓦斯事故，井下新水平、新区投产时瓦斯涌出量预测必不可少。此项参数是井下通风、瓦斯日常管理不可缺少的基础参数。传统瓦斯涌出量预测目标是采用矿山统计法或分源预测法结合地质、采掘等多重影响因素选取参数进行预测工作。实际现场中，瓦斯动力现象的准确预测对接续安全生产至关重要。

近年来随着智慧矿山的提出，以人工智能为导向的数字技术在煤矿飞速发展[1-2]。目前，国内外众多学者多采用机器学习算法进行瓦斯涌出量预测。付华等[3]提出了基于CIPSO和ENN的耦合算法，通过参数实时寻优对预测模型收敛速度、预测精度和鲁棒性进行提高；师超等[4]引入了一次指数平滑法进行数据优化，通过蛙跳算法优化Verhulst模型背景值参数建立SFLA-Verhulst组合预测模型；肖鹏等[5]压缩映射遗传算法优化BP神经网络，并采用核主成分分析法对影响因素数据集进行降维，构建CMGANN耦合算法；Yuan[6]利用传统的GM(1,1)模型预测瓦斯涌出量，模型能够实现实时、动态指导。

上述学者的探索对瓦斯涌出量预测工作均有所推进。考虑瓦斯涌出量影响因素较为复杂，以优化数据特征、提高综合模型质量为目标。基于此，以沈阳某煤矿综采面瓦斯涌出量历史数据为对象，搭建1种融合Lasso回归与随机搜索优化XGBoost的模型进行瓦斯涌出量预测，采用Lasso回归筛选出瓦斯涌出量的重要影响因素，得到经特征选择后的样本数据。结合随机搜索调参后的XGBoost模型得到预测值，引入评判指标验证模型有效性。

1 模型构建

1.1 Lasso回归模型

套索回归首次提出于1996年，通过降阶的思想对数据进行压缩估计，其通过构造1个惩罚函数得到1个较为精炼的模型，对回归系数进行压缩并使部分回归系数变为0，从而进行变量的筛选[7-8]。

该算法可有效地从高维变量中选取与涌出量相关的自变量，实现降维目的。该过程只进行筛选影响因素，不进行预测。

Lasso回归系数β可以对式(1)求最小值得到：

(1)

式中：第1项为残差平方和；n为瓦斯涌出量样本数；p为瓦斯涌出量影响因素个数；β0是xij为0时yi的均值；βj为回归系数；yi为因变量瓦斯涌出量值；xij为自变量第i行样本第j个输入值；第2项为压缩惩罚；λ为正则化参数。

正则化参数λ控制这2项对回归系数估计的相对影响程度，其数值确定方法为交叉验证。

1.2 XGBoost模型

极限梯度提升XGBoost是2016年由陈天奇提出的，其在大多数回归和分类问题上表现良好，应用在人工智能、工业等多个领域[9-11]。将其原理与瓦斯涌出量相结合如下：

设D={(xi,yi)}(|D|=n,xi∈Rm,yi∈R)，其中n为瓦斯涌出量样本数；m为样本包含的特征数；xi为样本数据；yi为样本真实值。模型在样本上的预测结果如式(2):

(2)

(3)

式中：l为可微凸损失函数；γ和λ为正则化参数。

(4)

对式(4)中新预测值进行二阶泰勒展开，并去除常数项，其表达式如式(5)：

(5)

式中：gi和hi分别为损失函数中一阶梯度和二阶梯度数据。

假定Ij={i|q(xi)=j}表示第j组叶子节点，展开正则项得到式(6)：

(6)

(7)

(8)

1.3 XGBoost模型参数寻优算法

网格搜索算法，人为地分配1个特定的参数范围，设置调整参数的步长，利用调整的参数训练学习器，并使用交叉验证来评估性能。拟合函数尝试所有参数组合后，最优参数将返回给适宜的学习器，并调整为参数最佳组合。但是该寻优过程耗时较多，效率较低[12]。

随机搜索算法，通过选择每1个超参数的1个随机值的特定数量随机组合从而大大减少超参数搜索的计算量，缩短寻优时间，提升模型性能。其在空间分布中是以随机采样的方式进行的，对于连续变化的参数，随机搜索算法将其作为1个分布进行采样。

网格搜索算法与随机搜索算法示意如图1所示。

图1 网格搜索与随机搜索算法示意Fig.1 Grid search and random search algorithm schematic

2 随机搜索+XGBoost预测模型

本文首先通过特征选择中的Lasso回归对数据样本进行筛选，去除对模型训练中没有积极贡献的特征，选用随机搜索算法优化XGBoost模型参数，构建“随机搜索+XGBoost”预测模型，具体的流程步骤如下：

1)Lasso回归建模：通过交叉验证确定正则化参数λ，从回归系数中筛选出没有积极贡献的特征。

2)划分样本：Lasso回归选出主要影响因素后，更新后的数据作为预测输入，并将新的样本数据进行训练、测试样本的划分。

3)初始化XGBoost模型参数：使用树的数量n_estimators，最大树深度max_depth，学习速率learning_rate，叶子上最小样本数min_child_weight。

4)确定最优参数：给定参数区间，设定随机搜索的种子数，利用随机搜索算法进行参数寻优，直到确定最优参数，判断是否满足预先设定要求。

5)模型对比：通过随机搜索+XGBoost预测模型得到预测值并与传统XGBoost模型与网格搜索+XGBoost模型进行评判指标对比分析。

3 瓦斯涌出量预测实验与分析

3.1 影响因素的选取

本文从初始瓦斯条件、开采条件、煤层地质条件这3个方面对瓦斯涌出量影响因素进行分析。

1)初始瓦斯条件：开采层瓦斯含量是瓦斯涌出的决定性因素，开采层瓦斯含量高会导致瓦斯涌出量高。由于预抽采瓦斯会对瓦斯涌出量产生显著影响，此处假设本煤层预抽采时间固定为2 a。当本煤层瓦斯含量不高时，由于邻近煤层赋存瓦斯含量较高，开采时瓦斯会涌入开采层及采空区。另外，邻近层厚度、煤层间距、层间岩性也会间接影响瓦斯涌出[13]。

2)开采条件：综采面产量的增减与绝对瓦斯涌出量有明显的线性关系，涌出的瓦斯主要来源于割煤机割落的煤块，一般来说，落煤时瓦斯涌出量较高。因此，采高、推进速度以及采出率等可作为瓦斯涌出的相关因素。

3)煤层地质条件：对于我国的开采地质条件，煤层埋深越深瓦斯涌出量越大。一般来说，深部煤层透气性较差，会造成瓦斯积聚。煤层、岩层的渗透性与构造破坏程度、采动裂隙等因素息息相关，采动裂隙又与工作面的长度、开采强度等因素有关。另外由于采掘的持续推进，煤层厚度、煤层倾角的变化，瓦斯的扩散释放也较为明显。

经过综合分析，确定与瓦斯涌出量相关的影响因素见表1。

表1 各影响因素回归系数Table 1 Regression coefficient of each influencing factor

3.2 Lasso回归方法筛选变量

通过查阅文献、结合前人成果，本文以沈阳某矿瓦斯涌出量影响因素数据为例，样本数据源于文献[14]，通过Lasso回归进行影响因素特征选择。

由于瓦斯影响因素众多，直接代入XGBoost模型预测会造成模型复杂度过高。因此，本文选用特征工程中的Lasso回归方法，通过R语言编程对影响较小的因素进行剔除。Lasso回归通过交叉验证确定模型的惩罚力度。交叉验证过程如图2所示。

通过图2可看到λ在不同取值下各变量惩罚函数值的变化情况，经交叉验证得到的正则化参数λ的值为0.012 56，1倍标准差值为0.061 05。由公式(1)原理，通过得到的正则化参数λ，可知各个影响因素的回归系数。Lasso回归系数变化轨迹如图3所示，各影响因素回归系数统计见表1。

图3 Lasso回归系数变化轨迹Fig.3 Lasso regression coefficient change trajectory graph

由表1和图3结合可知，当正则化参数λ的值为0.012 56时，此时有5个变量的惩罚函数值收敛为0，表明这5个变量对模型训练没有积极贡献，故将这5个变量剔除。

通过Lasso回归筛选影响因素后，部分数据样本汇总见表2。

表2 瓦斯涌出量影响因素数据集(部分数据)Table 2 Data set of influencing factors of gas emission (partial data)

3.3 搜索算法参数寻优

由于XGBoost模型参数较多，过多的参数寻优会造成寻优时间过长，本文选取如下4个主要参数通过Python进行寻优：1)使用树的数量n_estimators；2)最大树深度max_depth，一般用于防止过拟合；3)学习速率learning_rate，随着权重的减少，模型鲁棒性会有所提升；4)叶子上最小样本数min_child_weight，其内涵是最小样本的和，和最大树深类似，局部的特殊样本可以通过其取值进行有效避免。参数寻优范围及结果见表3。

表3 超参数寻优范围及结果Table 3 The optimization range and results of super parameters

3.4 随机搜索+XGBoost模型预测结果分析

将样本数据后10组作为测试集，利用随机搜索+XGBoost模型对测试集进行预测，并将预测结果与传统XGBoost模型和网格搜索+XGBoost模型进行对比，对比其他模型结果和相对误差见表4。搜索优化模型预测结果对比如图4所示。

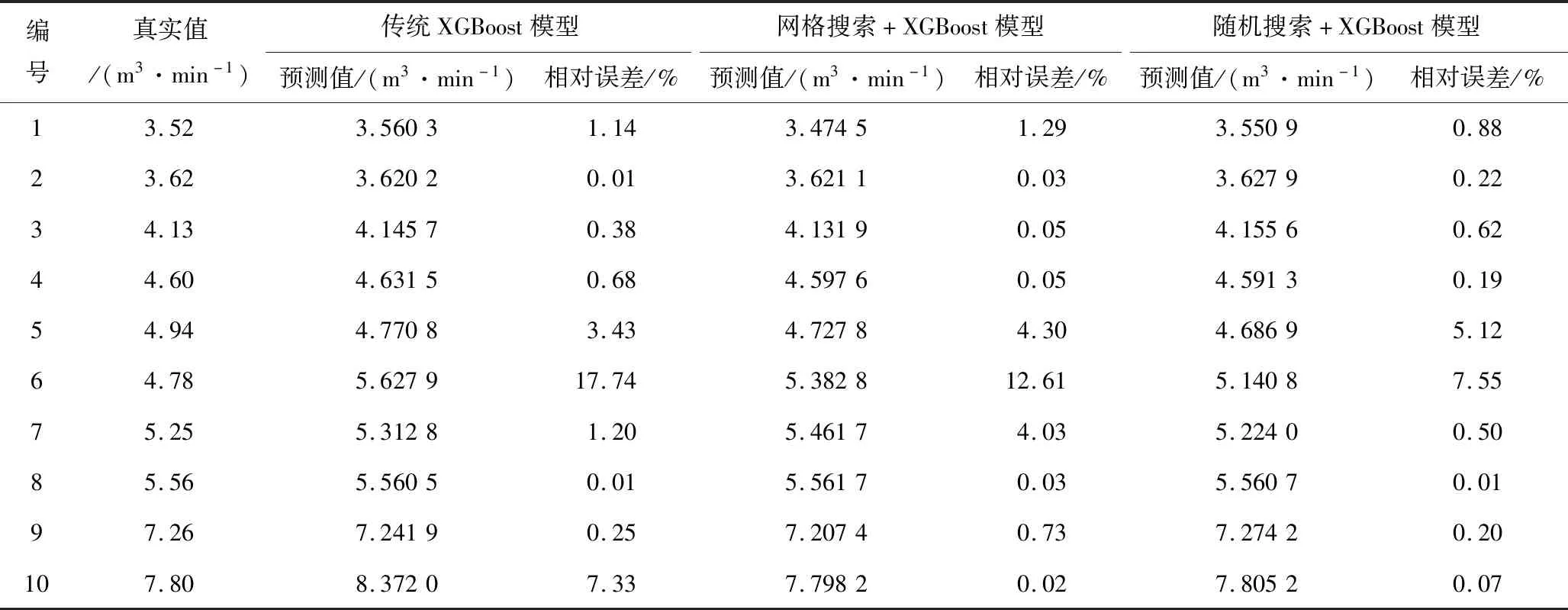
表4 各模型瓦斯涌出量预测结果及相对误差Table 4 Prediction results and relative errors of gas emission of each model

图4 搜索优化模型预测、实际值对比Fig.4 Search optimization model prediction and actual value comparison

从整体上来说，传统XGBoost模型和网格搜索+XGBoost模型平均相对误差分别为3.22%，2.31%。本文的随机搜索+XGBoost预测模型平均相对误差为1.53%，可看出本文模型精度的提升较为明显。

从个别数据上考虑，如编号2，3的3种模型相对误差均小于1%，差距不大，此时均能够满足工程上面的需要。

对于3种模型相对误差计算结果偏差较大的数据，如编号5～7，本文模型与其他2种模型比较，编号5相对误差略高于其他2种模型，编号6，7相较其他2种模型提升较多。其他2种模型最大相对误差均高于一般工程允许的最大误差10%，本文模型最大相对误差为7.55%，表明本文模型能够满足工程实际需要。

采用均方根误差RMSE用来衡量拟合效果，均方根误差越小，预测精度越高；希尔不等系数TheilIC，评价预测结果相对真实结果，拟合误差指数通常在0到1之间，数值越小表明计算值与真实值的差异越小，即计算结果精度越高[15]。分别如公式(9)，(10)所示。

(9)

(10)

各模型评判指标对比如表5所示。

表5 各模型评判指标对比Table 5 Comparison of evaluation indexes of each model

由表5可知，本文模型与传统XGBoost模型和网格搜索+XGBoost模型相比，平均相对误差分别下降了1.69%，0.78%，精度有明显提升。

经过计算，传统XGBoost模型、网格搜索+XGBoost模型和随机搜索+XGBoost模型3种模型的均方根误差分别为0.328 9，0.214，0.140 3 m3/min，希尔不等系数分别为0.030 5，0.02，0.013 2，由此可见随机搜索+XGBoost模型预测精度最高、泛化能力最强。

4 结论

1)从初始瓦斯条件、开采条件、煤层地质条件3个方面分析瓦斯涌出量影响因素，发现各影响因素之间多重相关；通过特征工程中Lasso回归模型对瓦斯涌出量影响因素进行筛选，当正则化参数取0.012 56时，确定瓦斯涌出量主要影响因素，降低建模难度。

2)由于XGBoost模型参数较多，本文主要选取n_estimators，learning_rate，max_depth和min_child_weight4个主要参数通过Python在一定范围内进行参数寻优。将网格搜索、随机搜索与XGBoost模型结合后预测结果进行对比，本文模型选取的最优参数组合分别为522，0.054，4，3。

3)传统XGBoost模型、网格搜索+XGBoost模型和随机搜索+XGBoost模型3种模型的均方根误差分别为0.328 9，0.214，0.140 3 m3/min，希尔不等系数分别为0.030 5，0.02，0.013 2。由此可见，随机搜索+XGBoost模型指标评价综合能力较高，可为现场瓦斯防治工作提供理论基础。