基于差分进化-NM单纯形法的危化品泄漏源定位*

陈增强，高艺博，陈成功，吕宝源，王心哲

(北京石油化工学院 信息工程学院，北京102617)

0 引言

危化品泄漏事故的发生，可能造成人员和财产的巨大损失。确定泄漏源的源强和位置信息，明确泄漏影响范围，是对人员和重要财产进行疏散和转移的关键。

泄漏源定位的典型策略有：烟羽跟踪[1]、多机器人合作[2-4]、概率估计[5]、反算寻优[6]等。近些年，许多学者将群智能算法与扩散模型相结合，用于泄漏源定位的研究，如遗传算法[7]、模拟退火算法[8]、粒子群算法[9]、蚁群算法[10]、果蝇优化算法[11]等。由于单一的优化算法在泄漏源源强反算中存在一定的局限，许多学者开始关注混合算法，例如：陈增强[12]将遗传算法和模式搜索算法相结合，用于毒气泄漏源源强反算，不仅避免了遗传算法过早收敛问题，而且避免了模式搜索算法对初值敏感的问题；张建文等[13]提出混合遗传-Nelder Mead单纯形算法反算泄漏源源强及位置，通过实验证明混合后的算法可以快速准确地反算出结果；蒋彦等[14]将差分进化算法和模式搜索算法结合，将差分进化算法计算过程中没有达到收敛的结果作为模式搜索算法的初始值，计算出最终的结果，提高了算法精度。相关研究表明，通过不同算法的优势互补，可以快速准确地反算出泄漏源源强及位置。

差分进化(Differential Evolution，DE)算法于1997年由Storn等[15]提出，该算法的参数较少，易于实现；但是算法精度不高，寻优效果较差，尤其是在算法后期，种群趋于逐渐收敛的状态，个体间差异性较小，容易造成早熟收敛，搜索停滞的问题[16]。因此本文提出1种混合差分进化-Nelder Mead单纯形算法(DE-NM)应用于危化品泄漏源定位。首先用DE算法进行全局寻优，在执行变异、交叉、选择操作之后，将得到的种群结果作为NM算法的初值，进一步搜索最优结果。

1 源强反算模型

(1)

式中：(x0,y0,z0)是泄漏源的位置坐标，m；Q0是泄漏源的源强，g。

利用优化算法进行迭代寻优，使得目标函数值最小的1组参数，就是要求的最优泄漏源强和位置。

2 混合差分进化-Nelder Mead单纯形算法

2.1 改进的差分进化算法

差分进化算法主要是利用变异、交叉、选择操作进行优化。差分进化算法步骤如下：

1)设置算法参数：种群规模NP、基因长度D、初始放大因子F0、交叉概率CR、迭代次数iter_max、范围domx等。

2)初始化种群,随机生成初始个体，如式(2)所示：

(2)

式中：domx(i,1)是范围矩阵；rand(NP,1)是随机函数。

3)计算种群的适应度值，选出当前最优个体zbest以及最优适应度值bestfitness。

4)迭代开始，先执行变异操作。对于当代第i个个体Xi(t),i=1,2,…,NP，进行差分变异如式(3)所示：

Xi(t+1)=Xi(t)+F*[Xj(t)-Xk(t)]

(3)

式中：Xi(t+1)是产生的新个体；Xj(t)，Xk(t)表示种群中除去当前个体，随机选取的2个互不相同的个体；F为放大因子，在此引入1种新的自适应性函数，以提高算法后期的收敛精度。动态变化的放大因子F表达式如式(4)所示：

F=F0*{exp[iter_max/(iter_max+gen)]-1}

(4)

式中：gen是当前代数。

5)执行交叉操作，如式(5)所示：

(5)

6)利用“贪婪原则”进行选择操作，即在每一次迭代计算中，将当前个体Xi(t)和Xi(t+1)进行适应度函数值的比较，如果Xi(t+1)的适应度值优于Xi(t)，就代替当前个体成为下一代的父代；否则，直接进入下一代。

7)计算新种群的适应度值，如果优于全局最优适应度值，则更新全局最优解zbest以及最优适应度值bestfitness；否则，不更新。

8)判断是否达到预先设定的最大迭代次数。若达到，则输出群体最优解；否则，返回4)。

2.2 Nelder Mead算法

(6)

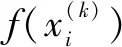
对单纯形顶点进行一系列的反射、扩张和收缩操作，如式(7)～(9)所示：

(7)

(8)

(9)

(10)

重复进行反射、扩张和收缩操作，直到构造的单纯形满足要求为止。Nelder等[17]提出了Nelder Mead单纯形算法的终止准则，如式(11)所示：

(11)

式中：ε是1个大于0的常数。

2.3 混合策略

DE算法虽然有可能实现全局最优解搜索，但也有可能出现过早收敛的弊端；NM算法对初值的要求较高。因此将2种算法结合，首先，利用DE算法进行全局寻优，执行变异、交叉、选择操作，然后，将得到的新种群作为NM算法的初值，每隔5代执行1次NM算法，进一步搜索最优结果。DE-NM算法的流程图如图1所示。

图1 混合差分进化-NM单纯形算法流程Fig.1 Flow chart of hybrid differential evolution-NM simplex algorithm

3 结果与讨论

3.1 高斯模型

高斯瞬时模型如式(12)所示：

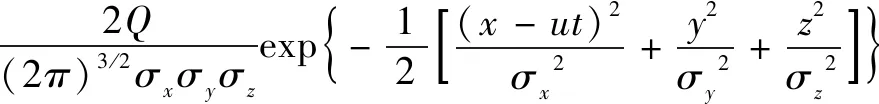
(12)

式中：C(x,y,z,t)是(x,y,z)点t时刻的浓度值，g/m3；Q是污染源的释放强度，即源强，g；(σx,σy,σz)是x，y，z方向浓度分布的标准差，即扩散系数，m；u是风速，m/s；t为释放经历的时长，s。扩散系数计算可参考文献[13]。

(13)

将式(13)代入式(1)，则目标函数如式(14)所示：

(14)

3.2 仿真实验结果

为验证DE-NM算法对危险化学品泄漏源定位的可行性，假设泄漏源强为Q0=2 000 g，泄漏位置为x0=50 m，y0=15 m(考虑地面的情况，设z0=0)，大气稳定度为F级，平均风速为2 m/s，时间为100 s。

DE-NM算法的参数设置如下：种群规模NP=100，基因长度D=3，放大因子F0=0.4，交叉概率CR=0.1，迭代次数iter_max=100。

利用DE-NM算法对目标函数式(14)进行优化，得到的反算结果如表1所示。

表1 DE-NM算法反算结果Table 1 Inverse calculation results of DE-NM algorithm

从表1可以看到Q0，x0，y0的反算结果相对误差分别为3.0%，0.2%，0.7%，反算结果误差较小，表明利用该算法进行事故源定位能够较为精确获取源强和位置信息。

DE-NM算法反算参数Q0、x0，y0的寻优过程如图2所示。图2中实线表示源强Q0、位置x0，y0的变化，虚线表示对应参数的期望值。从图2中可见，在搜索过程中3个参数都能够快速收敛到期望值；搜索过程中即使初值远离期望值，最终也能够收敛到期望值。表1和图2的结果验证DE-NM算法在危化品泄漏源定位问题中的可行性。

图2 DE-NM算法反算结果寻优过程Fig.2 Optimization searching process on inverse calculation results of DE-NM algorithm

由于DE-NM算法初值选取的随机性，每次运行结果不完全相同。算法独立运行20次的结果分布如图3所示。

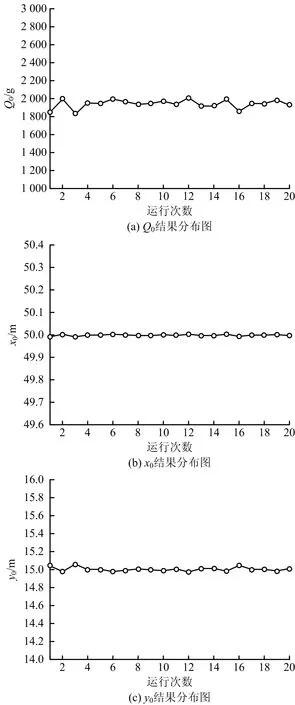
图3 DE-NM算法独立运行20次的结果分布图Fig.3 Distribution of results of DE-NM algorithm running 20 times independently

从图3可以看出3个变量20次反算结果离散程度较小，反算结果较为稳定。

进一步，表2统计DE-NM算法独立运行20次得到Q0，x0，y0的平均值、相对误差以及标准差。

表2的统计结果表明独立运行20次的平均值相对误差较小，各参数的标准差也较小，验证DE-NM算法稳定性较好。

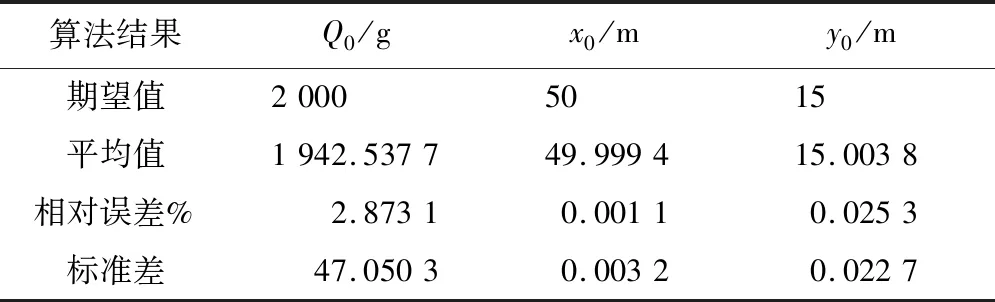
表2 DE-NM算法独立运行20次的结果Table 2 Results of DE-NM algorithm running 20 times independently

3.3 不同算法比较分析

为了验证DE-NM算法的优势，将其结果与DE算法、NM算法进行比较，对比结果如表3所示。DE-NM算法以及DE算法不受初始值的影响，采用随机生成的方式，NM算法对初始值有较高的要求，因此分别选取距离期望值较近的1组数据以及距离期望值较远的1组数据。

表3 不同算法的泄漏源反算结果对比Table 3 Comparison on inverse calculation results of leakage source by different algorithms

由表3分析可知：DE-NM算法的反算结果与期望值的误差较小，反算结果较为精确。NM算法在初值选取接近于期望值时，误差较小；而当初值选取远离期望值时，误差较大。DE算法的反算结果与期望值误差较大。比较结果表明DE-NM算法的反算结果，优于单独使用DE算法或单独使用NM算法的反算结果。

3.4 算法混合间隔的影响分析

对DE-NM算法中NM算法不同间隔代数的结果进行比较分析，结果比较如表4所示。

表4 执行NM算法不同间隔的结果对比Table 4 Comparison on results of NM algorithm executing different intervals

表4结果表明，NM单纯形算法执行的间隔代数对结果的精度影响较小，在运行时间上有所不同。因此可以根据具体问题对运行时间的要求进行间隔代数的合理选取。

4 结论

1)利用DE-NM算法对危化品泄漏源进行定位，可避免DE的过早收敛问题，以及NM的初值依赖性，进而提高定位精度。

2)基于DE-NM算法的定位结果与期望值误差较小，定位精度较高，并且多次运行结果离散程度较小，算法具有较好的稳定性。

3)对比单一算法，DE-NM算法可以快速准确地对泄漏源进行估计，能够为应急决策提供帮助。