液体气溶胶粒子间相互作用的仿真研究

胡 卉， 崔 洋， 徐 震， 关 甜 ， 马骊溟

(1. 长安大学运输工程学院， 西安 710000； 2. 长安大学汽车学院， 西安 710000 )

1 引 言

在日常活动中, 空气中可以较长时间飘浮着具有危害的气溶胶散射粉尘小粒子. 而气溶胶分散体系是由分散介质和分散相构成的. 其中以空气为主要分散介质, 由固体或者液体的小粒子组成了分散相, 在空气中漂浮的固体和液体小粒子则构成了相对固定的扩散体系[1]. 随着中国经济的高速发展，特别是经济发展迅猛的长三角、珠三角出现了区域性大气颗粒物污染现象，气溶胶污染日益成为大气污染控制的难点和痛点. 另外存在于空气中的气溶胶除了自身的污染危险, 粉末形式的环境金属物质存在很大的意外扩散可能性，导致吸入或皮肤接触[2-4]. 吸入被认为是最有可能和最直接的接触环境金属物质的途径[5]，但是皮肤渗透或摄入也可能无意中发生, 还能传播真菌和病毒，导致地区性疾病的流行和爆发[6]. 因此需要对气溶胶形成及扩散过程进行研究，为后续气溶胶的净化提供数据依据[7].

目前对气溶胶形成以及扩散的研究大都采用试验方法. 刘俊等[8]探讨了气溶胶浓度变化过程对雷暴云微物理过程、起电以及空间电荷结构所产生的影响，结合了某次山地雷暴案例，通过在传统的二元雷暴云起和放电模型中，加入云滴冻结因子的试验进一步验证了该理论. 韩雪[9]在一个密闭的空间内均匀地注入气溶胶粒子和空气，通过溜凝作用，注入粒子的直径将伴随着时间呈现一定的函数规律, 用这种结构近似模拟大气气溶胶在风作用下的演变过程. 文献[10]利用自主研制的大型室外光化学烟雾箱模拟系统，在接近真实大气环境条件下，开展烟雾箱实验，设计并制定科学具体的大气光化学烟雾箱模拟实验方案. 石茹琳等[11]在WRF-SBM模型中模拟了一次新疆夏季的冰雹天气过程, 通过气溶胶浓度对比, 对冰雹云的微物理特征、冰雹形成机理和降水过程的影响采用敏感性试验研究. 邓康清等[12]则利用内部流场-热力耦合的三维有限元流体FLUENT计算软件系统和暂态热分析软件系统, 分析了某种烟火型气溶胶发生器燃气流场情况, 从而得到了气溶胶散射的外表面温度场分布, 及其随燃料流量、发生器位置、气溶胶散射燃烧温度、工作持续时间等的改变, 以及气溶胶散射的运动规律. 任浩亮等[13]采用离散相模型模拟气溶胶颗粒在烟幕流场下的扩散规律. 张国强[14]在探索柴油-空气燃料爆轰燃烧的超细雾化的基础上，进一步研究在旋转连续爆轰燃烧室内柴油空气混合气溶胶运动规律，找到运动机理获取最佳雾化模型.

气溶胶越来越广泛地应用在国防、消防、农业、医学等领域，这就需要企业和科学家们不断利用其开发创新，来改善人们生活中的各个方面[15-17]. 其危害的一方面也更需要得到全社会的重视[18-20]. 然而, 在大规模场地进行试验会耗费大量的人力物力成本，并且气溶胶的有害影响存在不可控性[21,22]. 为了提高试验的效率和保证试验的安全可靠性，本文采用大型计算流体力学仿真软件STAR-CD进行研究. 首先，我们基于流体的物理和数学模型对液态气溶胶进行数值模拟；然后采用有限容积法模拟气溶胶在仿真环境中的扩散规律，获得气溶胶粒子在仿真环境中的浓度分布图；最后通过改变气溶胶来源数目和环境压强来对扩散规律进行研究.

2 液体气溶胶喷射数学模型及基本控制方程

流动的流体也要遵守基本的物理规律，通过不同的控制方程进行控制这些流体，从而能够描述流体流动的物理规律. 即：质量守恒方程，理想气体状态方程，动量守恒方程. 如果其中还有流动流体内部的不同成分之间的相互作用，还需要组分守恒方程.

(1) 质量守恒方程

可压缩流体的笛卡尔坐标系张量形式的质量守恒方程为：

(1)

公式中t为时间；ρ为密度；xi为笛卡尔坐标(i=1, 2, 3)；uj为流体在xi方向上的绝对速度分量；sm为质量原项.

(2) 动量守恒方程

流体动量守恒方程式为：

(2)

式中p表示压力；τ表示应力张量分量；si表示动量原项分量.

(3) 组分质量守恒方程

(3)

(4) 控制方程统一形式

从以上各式可以看出，尽管(1)(2)(3)中的具体变量不一样，但是它们反应的物理量守恒形式完全相同.如果用φ代表它们通用的变量，则以上控制方程可以统一表示为：

(4)

式中，φ可以代表求解变量；Γ为广义扩散系数；S为广义源项.

不过由于实际情况比较复杂，几乎都是湍流过程，因此需要更加精确的湍流模型.

3 仿真模型的建立

3.1 CFD解决问题基本步骤

用CFD解决问题需要建立模型，我们需要分别从几何材料、材料、求解控制、网格、边界条件及其他数值因素方面入手，确定研究物体的大小、形状和零部件相对位置等几何要求，明确研究对象的粘度、密度和沸点等物理参数，选择合适的物理模型以及正确的算法程序.

目前，大多数CFD软件解决问题基本工作流程如图1所示.

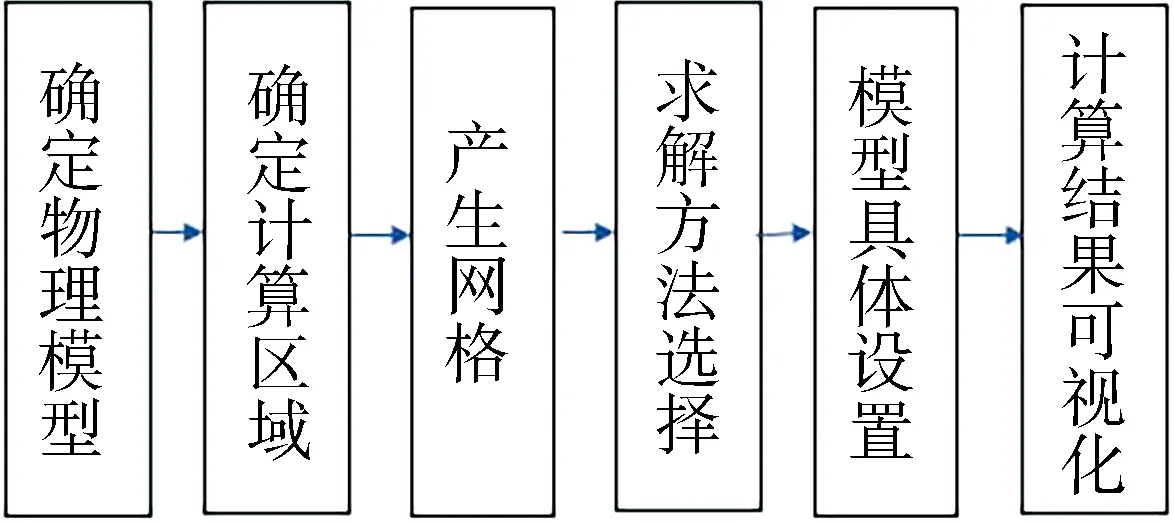
图1 CFD解决问题基本工作流程

3.2 离散方程的建立

STAR-CD的建立基础是有限容积法，而其方法核心是离散方式在区域上的建立.这个方法的实质就是以有限的点来代替之前区域中的无限个点，也就是将区域用网格进行划分，即：计算网格.目前的STAR-CD可以形成多种形状的多面体网格，四面体、六面体甚至不规则的多面体.

就二维问题而言，有限容积法的经典网格如图2所示.P为网格上随意选定的一个点，E、W、S、N分别是east、west、south、north的首字母缩写，分别代表P点东、西、南、北四个方向的相邻节点的标记.e、w、s、n则是指东、西、南、北四个区域的标记.由此形成的二维定常坐标系中，二维有限差分方程的一般形式为：

αPφP=αEφE+αWφW+αSφS+αNφN+SC

(5)

在三维非定常坐标系中，三维有限差分方程的典型形式为：

αHφH+αLφL+SC

(6)

其简写形式为：

αPφP=∑αIφI+SC

(7)

表达式中α为差分方程的系数;SC为常数项;上标0表示的是所选点P的前一状态;H和L分别表示第三维空间坐标上与P点相邻的两个网格点;I则表示与P点相邻的时间和空间的各个网点.

图2 二维差分问题的计算网格与控制体积

3.3 离散方程求解方法

目前STAR-CD中常用三种不同的算法,即SIMPLE、PISO和SIMPISO算法.由于本次仿真是一种非定常流动情况，故需要采用PISO算法.

PISO(Pressure Implicit Solution by Split Operator)算法是一种用分裂算子求解压力的隐式算法.这个算法主要适用于非定常流动，它有着很多优点，比如：针对压力场来说，它的校准精度较高.

PISO算法的一般求解步骤：

(1) 估计压力场p，并估计一个迭代初始速度场；

(2) 求解动量方程，得到速度场u，v，w；

(3) 求解p1′方程，得到p1′；用p1′来校正速度值；

(4) 求解p2′方程，得到p2′；用p1′和p2′来校正压力，即p=p+p1′+p2′；

(5) 求解那些通过源项、流体物性等影响流场的其他变量(如温度、浓度等)的离散化方程；

(6) 通过将新求得的速度代入方程得到新的压力值，再以新的压力值代入(2)中直至收敛；

(7) 得到收敛的最后的值，再依次求出其他的值.

3.4 物理模型

3.4.1 喷孔流动模型 本试验用图3所示的喷射分裂及雾化模型对柴油进行喷射以及雾化处理，以此近似代替液态气溶胶的生成过程.

图3 喷射分裂及雾化模型

本次试验的喷孔模型所采用的喷射规律如图4所示, 其质量流量m是不变的.

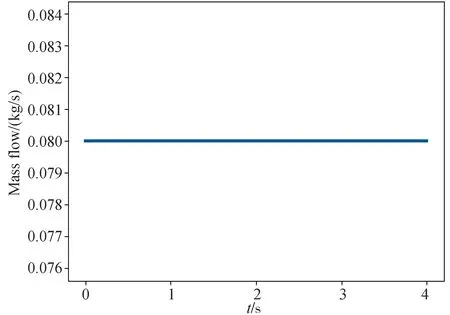
图4 喷孔喷射规律Fig.4 Nozzle jet pattern

质量流量m:

(8)

式中，ρ=708.25 kg/m3为所选液体C12H26的密度;d为喷射直径，本研究中d=0.2 mm；v为质量流率.

质量流率v计算方法：

(9)

其中，Cd=0.6为阻力系数；pabsolute为绝对压力；pinj为喷射压力.

pabsolute=pG+p0

(10)

式中，pG为相对压力;p0=1.013 25×105Pa为标准大气压.

仿真室内，根据其流动特点，选择拉格朗日多项流.

3.4.2 液滴雾化模型 本文采用的液滴雾化模型为Huh雾化模型.该模型的简单描述可以分为以下两个方面.

(1) 喷孔处产生的湍流在缸内形成扰动；

(2) 扰动持续增长，当达到一定程度，压力将会成指数成长.

喷孔出口处的平均湍动能：

(11)

喷孔出口处的湍流耗散率：

(12)

喷射液滴初始初始湍流长度及时间长度：

(13)

(14)

t时刻湍流长度及时间长度随时间衰减关系：

(15)

(16)

式中，U表示喷射的平均速度；L表示喷孔的长度;Kc表示形成损失系数;Kε是经验系数;Cμ为Huh模型系数.结果见表1.

表1 Huh雾化模型的系数

3.4.3 液滴撞壁模型 本文选择的是Bai碰壁模型[23]，这个模型主要是依据液滴所受的惯性力与表面张力之比的We数来决定的.

按照撞壁条件的不同共分为以下七种不同的撞壁类型[24].

(1) 粘附(Stick)撞壁液滴以球状粘附在壁面上，通常发生于低速能量较低的情况;

(2) 蔓延(Spread)撞壁液滴中速情况, 大面积粘合现象.

(3) 反弹(Rebound)液滴撞壁反弹回来;

(4) 反弹破碎(Rebound with breakup) 当TW≤TPR时，液滴不仅会从壁面上反弹回来并且会破碎;

(5) 蒸发破碎(Boiling-induced breakup) 当TW≈TN，液滴由于高温沸腾而破碎;

(6) 破碎( Breakup)当TW>TPA，液滴先是壁面形成油膜，然后油膜分散，形成不同的油膜区域;

(7) 飞溅(Splash)不规则的反弹破碎.

4 仿真室内环境建立

4.1 固定环境设计

4.1.1 基本模型及模型参数 本文采用以STAR-CD建立立方体对液态气溶胶在固定环境中传播进行模拟研究.通过建立立方体模型来模拟真实环境，本仿真模拟的是封闭环境内的传播.

如图5所示，本次研究所采用的模拟环境参数为40 mm×30 mm×120 mm的长方体.计算区域x,y,z方向网格数分别为40, 100， 120.

4.1.2 计算参数设定 由于本文情况属于非定常流动，所以我们采用PISO算法.计算松弛因子设定如表2所示.

图5 环境模型Fig.5 Environmental model

表2 计算松弛因子调整

4.2 操作界面展示

操作界面如图6所示.其中图6a开始界面可以选择参数设计，用于模型搭建以及参数选择；图6b为数据输出窗口，用于仿真数据输出；图6c为主窗口，为可视化区域，用于仿真结果的显示.

(a)开始界面(a) Start interface

(b) 输出窗口(b) Output window

(c)主窗口(c) Main window

4.3 仿真结果

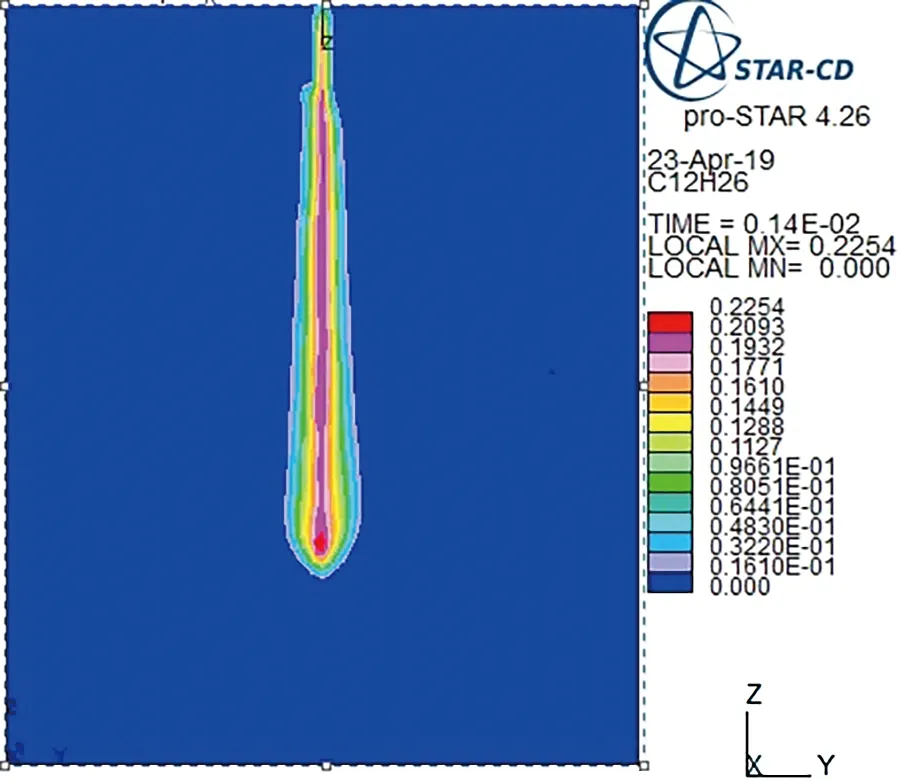
图7以及图9～图12为本仿真试验中的环境浓度场所示图. 图中的喷孔直径均为0.2 mm. 图中的颜色代表环境的浓度，其中蓝色代表环境浓度为浓度最低，红色部分表示浓度最高.图7a、7b、 7c和7d分别为当气溶胶模拟进入环境(0.4 MPa)中0.2、0.4、0.6和2 ms时液体气溶胶的扩散图.从图7可以得出，随着时间的推移，环境中的液体气溶胶会随着时间的增加导致气溶胶扩散，并且会随着时间的流逝大部分聚集在中下部分. 由图8可以看出单个来源液体气溶胶扩散直径随时间的变化，随着时间的增加扩散直径增加，并且在前1 ms内，扩散速度很快，随后速度逐渐减慢.

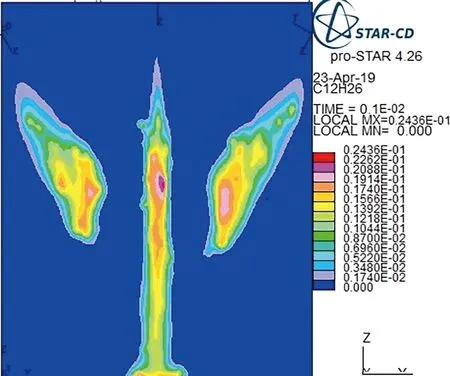
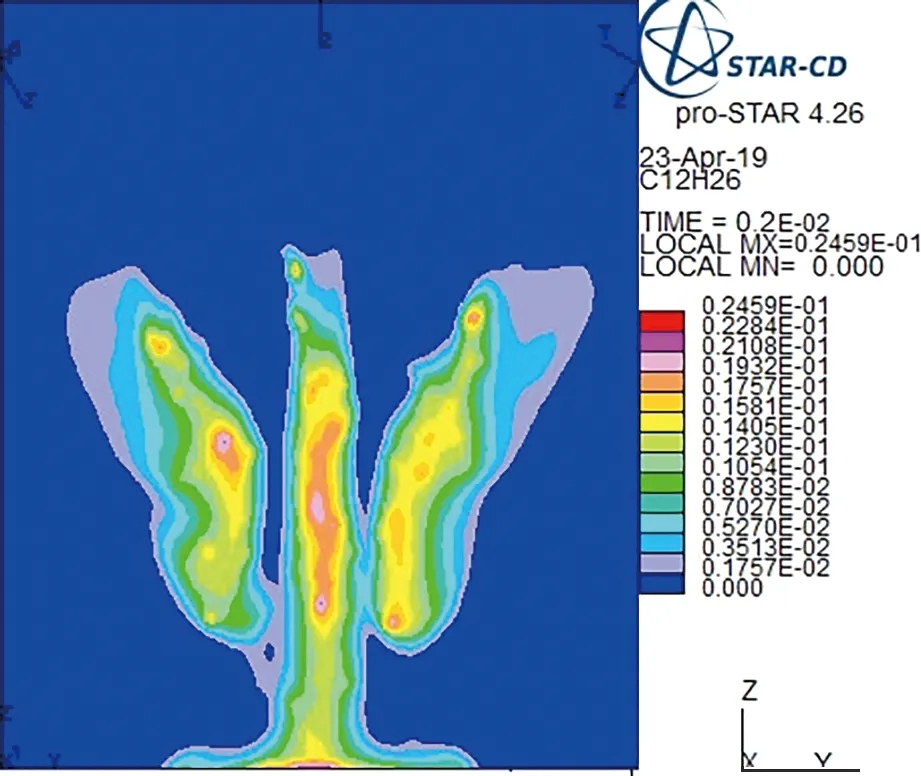
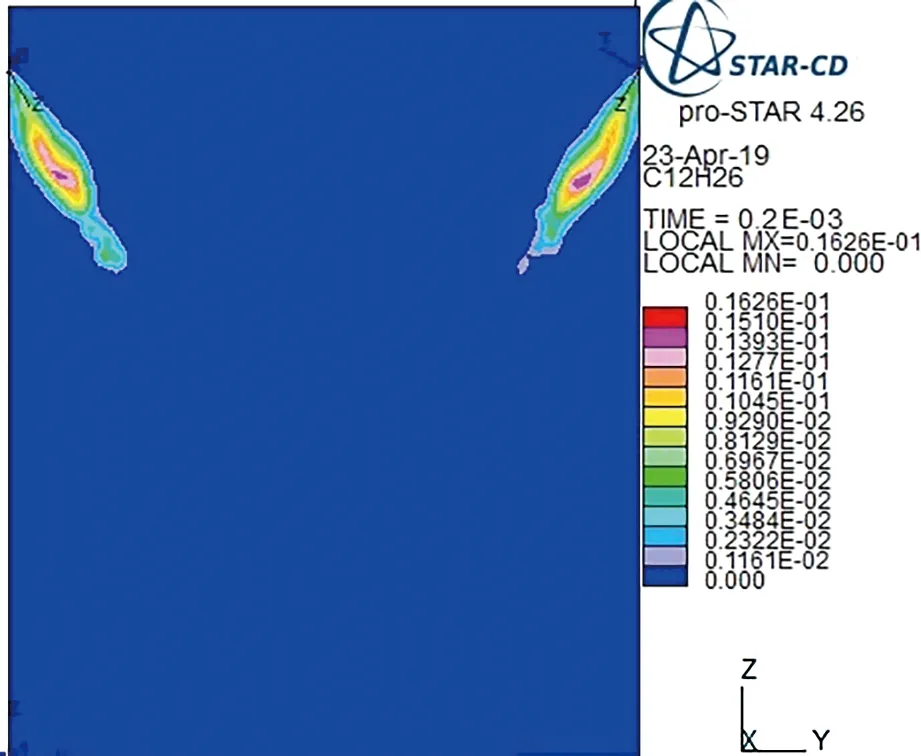
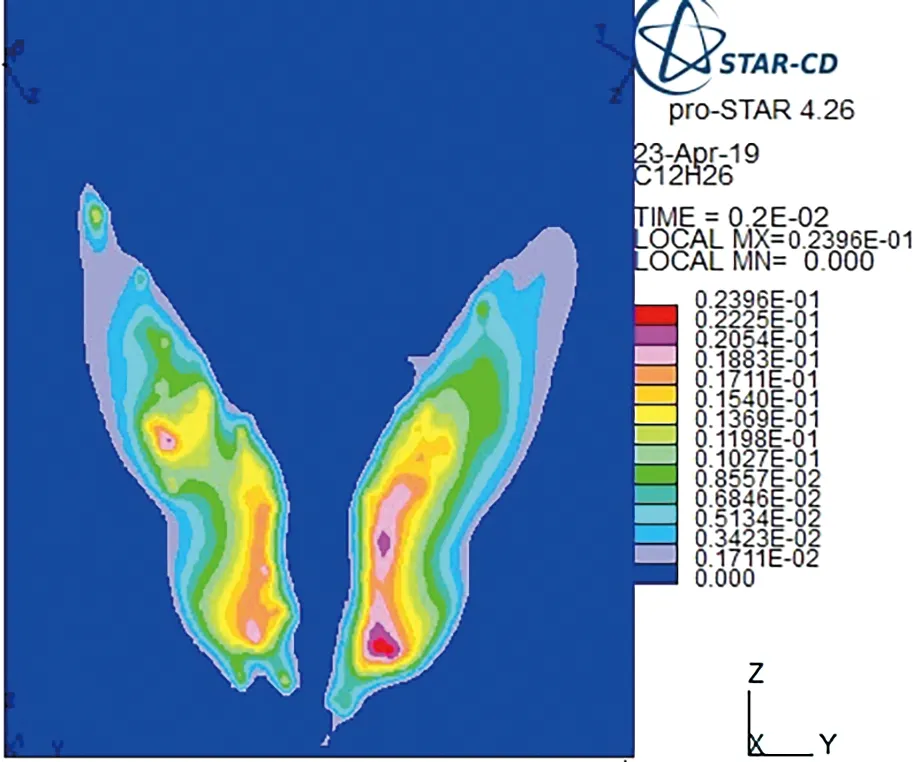
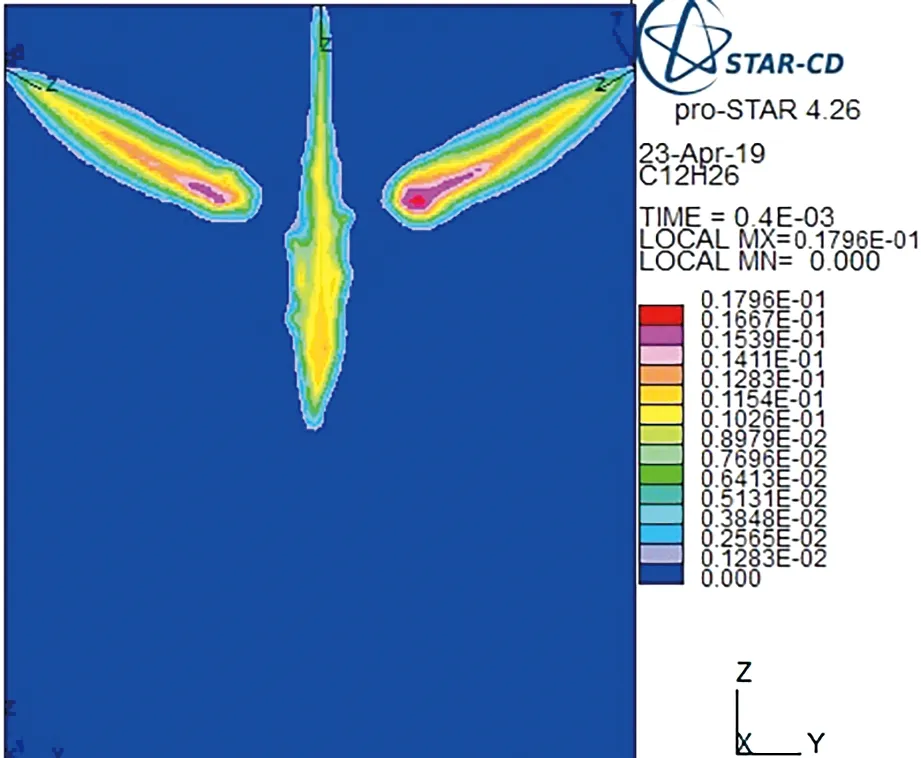
图9为多个液体气溶胶来源进入环境中时，液体气溶胶随着时间变化的传播过程图. 图9a、9b为两个来源(来源1和来源2)开始1和2 ms的仿真效果. 图9c、9d为三个来源(来源1、来源2和来源3)开始1和2 ms的仿真效果. 我们可以看出，在1 ms内，液态气溶胶的扩散速度很快； 随着时间的推移，当多个来源的液体气溶胶汇聚在一起时，整体对外的扩散速度减小，不同来源的液体气溶胶在汇聚的同时共同向下部扩散, 并且当液体气溶胶相互作用时，扩散速度减缓.

图10为改变环境压强(高压4 MPa)情况下得到的单个液体气溶胶来源的仿真实验情况. 图10a、10b、 10c和10d分别为0.2、0.6、1.4和2 ms时液体气溶胶的扩散图. 和图7进行对比，我们可以看出，当改变环境压强时，液态气溶胶在空气中的扩散速率变小.

图11为两个来源(来源1和来源2)模型在变换环境压强(高压4 MPa)情况下的仿真实验情况. 当改变环境压强时，液态气溶胶在空气中的扩散速率变小. 从图11可以看出，进行到2 ms时的扩散范围和低压(0.4 MPa)时的扩散范围一致. 但是随着时间的推移，扩散趋势仍然不变. 图12是三个来源的仿真情况，可以看出和图11具有相同的物理规律.

本节通过搭建仿真模型，模拟液态气溶胶，以长方体模型模拟气溶胶在固定环境中的扩散，对气溶胶在真实环境中传播进行模拟，分析真实环境中气溶胶粒子间的相互作用.

(a)0.2 ms

(b) 0.4 ms

(c) 0.6 ms

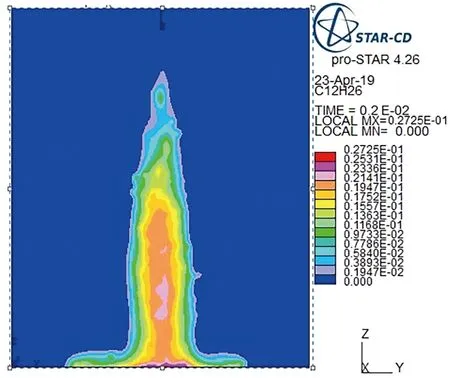
(d) 2 ms

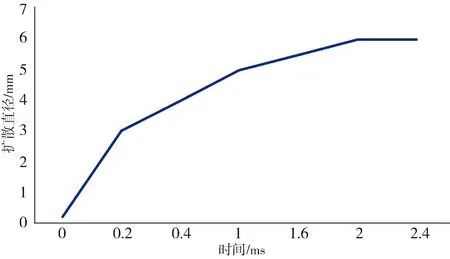
图8 单个来源液体气溶胶扩散直径和时间关系图

(a) 1 ms

(b) 2 ms

(c) 1 ms

(d) 2 ms

(a) 0.2 ms

(b) 0.6 ms

(c) 1.4 ms

(d) 2 ms

(a) 0.2 ms

(b) 0.4 ms

(c) 0.8 ms

(d) 2 ms

(a) 0.4 ms

(b) 0.8 ms

5 结 论

本文利用CFD软件STAR-CD对液态气溶胶形成的过程进行数值模拟研究，模拟液态气溶胶的扩散过程. 液态气溶胶连续注射到立方体模型中，持续释放固定的一段时间. 注射后，分散气溶胶的浓度被允许自然衰减一段时间. 我们得出以下结论：随着时间的推移，液态气溶胶在环境中扩散，并且在中下部聚集；当环境压强增加时，扩散速率减少；当有多个来源时，单个来源分开来看，扩散规律不变，但是当汇聚一起时，由于液态气溶胶之间的相互作用，整体扩散速率有所减少.