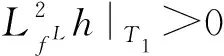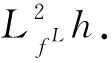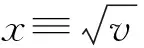Global dynamics of a planar Filippov system with a regular-SN
-, -
(School of Mathematics, Sichuan University, Chengdu 610064, China)
Abstract: In this paper, we investigate the global dynamics of a planar Filippov system with a regular-SN for general parameters not required to be sufficiently small. By analyzing the qualitative properties of the pseudo-equilibria, tangent points, equilibria at infinity as well as all kinds of periodic orbits, we obtain the global bifurcation diagram with eight bifurcation curves and give all global phase portraits in Poincaré’s disc.Some new bifurcation phenomena which do not appear in the case of small parameters is finded.
Keywords: Bifurcation; Boundary equilibrium; Filippov system; Global dynamics
1 Introduction
Filippov system consists of a finite set of equations
whereGi(i=1,…,m)are open regions separated by some (n-1)-dimensional submanifolds inRn. These submanifolds are usually called switching manifolds. Many practical applications use Filippov system, such as electronic[1], mechanical systems with dry friction[2]and neural activities[3].
Consider a two-dimensional Filippov system
(1)
whereα∈Rmandh(x,y;α)=0 is the unique switching manifoldΣ.Usually,fL(x,y;α),fR(x,y;α) are called the left half vector field and the right half vector field, respectively. Bifurcation analysis is one of the most important subjects in qualitative analysis of differential systems. In recent years, there are many results for smooth differential systems. As in smooth systems, many interesting bifurcation phenomena[1, 4, 5]can be observed as the parameters of system (1)change. A special form of system (1)
(2)
was investigated near the originO:(0,0), where (ρ,v)∈R2andρ,vare sufficient small[4]. Notice that the switching manifold in system (2) is a vertical linex=ρ, so that the projection of (v-x2,-y)Tin the direction of the normal vector of switching manifold is a constantv-ρ2. Thus, it is not hard to obtain that the whole switching manifold is either a sliding region ifv-ρ2>0, or a crossing region ifv-ρ2<0, or a set of tangent points ifv-ρ2=0.
There are some interesting problems[6-8], for instance, how about dynamical behavior for general parameters, how about dynamical behavior for non-vertical switching line, how about the global dynamical behavior.Motivated by these interesting problems, in this paper we investigate the global dynamics for system
(3)
where (ρ,v,k)∈R3andk≠0. By transformationsx→x,y→y/k, system (3) is equivalently rewritten as
(4)
where (ρ,v)∈R2. Whenρ=v=0, the originO:(0,0) is a regular point of the right half vector filed and a saddle-node of the left half vector filed, hence, we callOas a regular-SN of system (4). We equivalently investigate the global dynamics of system (4) for general (ρ,v)∈R2and obtain the following result.
Theorem1.1The bifurcation diagram of system (4) is shown in Fig.1 and consists of the following curves:
(i) the boundary equilibrium bifurcation curves:



(ii) the double tangency bifurcation curves:



(iii) the saddle-node bifurcation curves:


Global phase portraits of system (4) are given in Fig.2, whereA,B,Clie at (0,0),(1/4,0),(1/2,1/4) respectively, and

0<ρ<1/4},




-sgn(ρ)ρ2},ρ<1/4},

-∞<ρ<∞}.

Fig.1 Bifurcation diagram of system (4)
Note that (ρ,v) is considered generally inR2. We observe some dynamical behaviors which can not appear in the case thatρ,vare sufficiently small[6]. On the other hand, our result is global dynamics, not only restricted in a small neighborhood of the originO.
This paper is organized as follows. In Section 2 we recall some definitions and theory about Filippov systems.In Section 3, we give some lemmas and finally provide a proof for our Theorem 1.1.
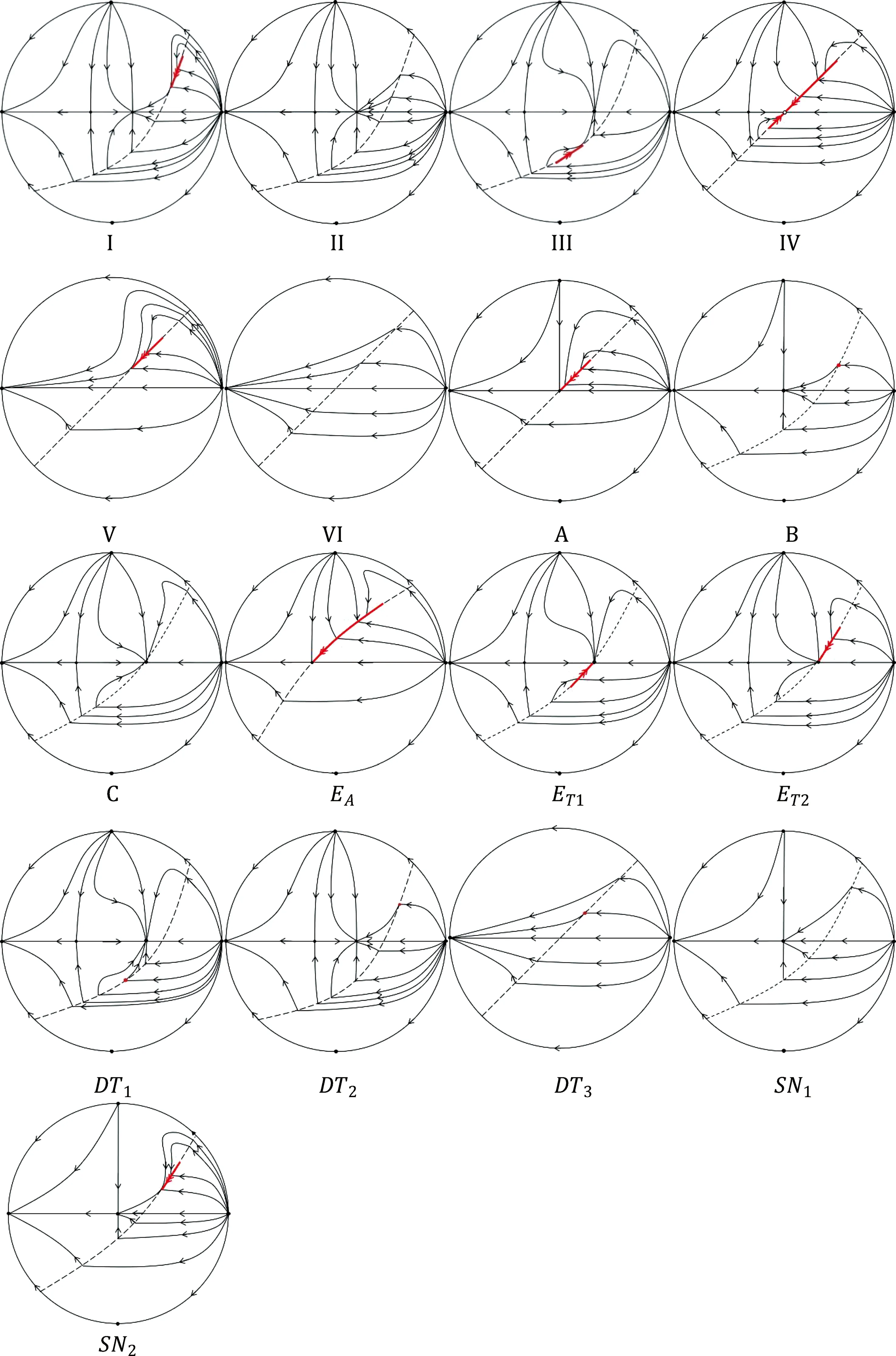
Fig.2 Global phase portraits of system (4)
2 Preliminaries
In Filippov system, we always focus on the result of how the orbit interacts with the switching manifoldΣ. Depending on the sign of normal components of left half vector field and right half vector field, we splitΣinto crossing regionΣcand sliding regionΣsas


whereLfh=〈grad(h),f〉 is the Lie derivative ofhwith respect to the vector fieldf. For (x,y)∈Σc, since the normal componentsLfLhandLfRhhave same sign, the orbit reaching (x,y) fromG1(G2) concatenates with the orbit enteringG2(G1). That is why we callΣcas crossing region. For (x,y)∈Σs, since the normal componentsLfLhandLfRhhave opposite signs, so the orbit reaching (x,y) slides along the switching manifoldΣ. By Filippov convex method[9], the sliding vector fieldfSthat governs sliding motion is given by
fS=λfL+(1-λ)fR
(5)
where
Denoting the numerator offSbyp(x,y),i.e.,

In order to figure out dynamics of Filippov system, as classic odes, we have to analyze singular points. According to Filippov’s approach[11], local singularity is caused by the vanishing of some functions such asfL,fR,h,p,LfLh,LfRhfor system (1). Point (x,y)∈GL(GR) is called an admissible equilibrium iffL=0 (resp.fR=0) is satisfied at that point and called a virtual equilibrium iffR=0 (resp.fL=0) is satisfied at that point. Point (x,y)∈Σis called an admissible pseudo-equilibrium (resp. a virtual pseudo-equilibrium) ifLfLh·LfRh≠0,fR·LfLh-fL·LfRh=0 are satisfied at (x,y)∈Σs(resp. (x,y)∈Σc). Point (x,y)∈Σis called a boundary equilibrium iffL=0 orfR=0 and called a tangent point ifLfLh·LfRh=0 andfL≠0,fR≠0.Moreover, if at point (x,y)∈Σwe have

(6)
we call it a cusp or a double tangent point. Similar definitions hold for the vector fieldfR.
For system (4), we have grad(h)=(1,-1)T, so that
LfLh=v-x2+y,LfRh=-1,
where
fL(x,y;v)=(v-x2,-y)T,
fR(x,y;v)=(-1,0)T,
h(x,y;ρ)=x-y-ρ.
According to definition of sliding regionΣs, we obtain it by solving inequalityv-x2+y≥0. Let

By a straight calculation we getΣs=∅ ifv<ρ-1/4 and
x-y-ρ=0}
(7)
ifv≥ρ-1/4. The boundary of the sliding region is
which consists of boundary equilibria and tangent points. By (5) we have
from which we getfS=0 if and only if (x,y)=(ρ,0). By (7), we have the point (ρ,0) is an admissible pseudo-equilibrium if and only if
v>ρ-1/4,
i.e.,v>ρ2.
3 Proof of the main result
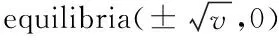
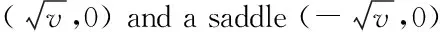
Lemma3.1In the casev>0, system (4) has a saddle and a stable-node ifv<ρ2andρ>0, a saddle ifv>ρ2, and no equilibria ifv<ρ2,ρ<0. In the casev=0, system (4) has a saddle-node ifρ>0 and no equilibria ifρ<0. In the casev<0, system (4) has no equilibria.


In the casev=0,fLhas a saddle-node(0,0). Thenh(0,0;ρ)=-ρ<0 ifρ>0 andh(0,0;ρ)=-ρ>0 ifρ<0. It implies that system (4) has a saddle-node forρ>0, no equilibria forρ<0.
In the casev<0, system (4) has no equilibria becausefLhas no equilibria.
Notice that ifv=ρ2, there is an equilibrium(ρ,0) offLonΣ, so thatfL=0 andh=0 at (ρ,0). This is to say,(ρ,0) is a boundary equilibrium of system (4) ifv=ρ2.
In the following we analyze equilibria of system (4) at infinity. Using Poincaré transformationsx=1/z,y=u/z, which change the infinity of thexy-plane to theu-axis of theuz-plane. We write system (4) as
(8)
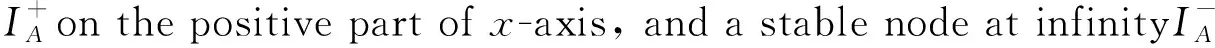
By Poincaré transformationsx=w/z,y=1/z, which change the infinity of thexy-plane to thew-axis of thewz-plane, system (4) is transformed into
(9)

where
G(θ)=sinθcos2θ-vsin3θ,
H(θ)=sin3θ+sinθcos2θ-cos3θ+
vsin2θcosθ.
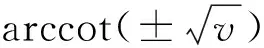

ProofSince
G′(0)H(0)=G′(π)H(π)=-1,
by Theorem 3.7 of Chapter 2 of Ref.[10], system (9) has a unique orbit approaching (0,0) asτ→+∞ orτ→-∞ in the directionsθ=0,π. Then we investigateθ=π/2, which only appear in the casev=0. By the transformationθ′=θ-π/2, we obtain thatG(θ′)=cosθ′sin2θ′. Since the Taylor expansion ofG(θ′)is
i.e.,G(θ′)=(θ′)2+h.o.t. As shown in Ref.[12], in directionθ=π/2, system (9) either has an infinite number of orbits approaching (0,0) asτ→+∞ orτ→-∞, or no orbits approaching (0,0) asτ→±∞. We obtain
(10)
in the casev=0, and system (10) has a solutionw=0. Because of dz/dτ>0(z≠0), we find an orbit leaving(0,0) asτ→+∞ in directionθ=π/2. Therefore, system (9) has an infinite number of orbits approaching (0,0) asτ→-∞, in directionθ=π/2. Similarly, we can prove the conclusion ofθ=3π/2 in this lemma.
Let




G′(θ)=cos3θ-2sin2θcosθ-3vsin2θcosθ
and sinθ1>0,v>0, we have
H(θ1)=sin3θ1(v+1)>0.
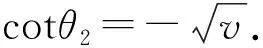
H(θ2)=sin3θ2(v+1)<0,
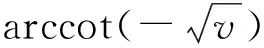
Lemma3.3For the casev>ρ-1/4,v≠ρ2, the fold (K1/2,K1/2-ρ) offLis visible ifρ>1/2v<ρ2, and is invisible eitherρ<1/2 orρ>1/2,v>ρ2; the fold (K2/2,K2/2-ρ) offLis visible ifρ<1/2,v<ρ2, and is invisible eitherρ>1/2 orρ<1/2,ρ2 Firstly, we analyze the tangent pointT1with conditionsv>ρ-1/4,v≠ρ2. By straight calculation, we have v<ρ2⟹4v<4ρ2⟹1-4ρ+4v<(1-2ρ)2⟹ v>ρ2⟹4v>4ρ2⟹1-4ρ+4v>(1-2ρ)2⟹ We can prove the conclusion ofT2by the same strategy. Lemma3.4System (4) has no periodic orbits. Finally, the results of saddle and saddle-node can be proved similarly. Having Lemmas 3.1~3.4, in the following we give a proof for Theorem 1.1.