结合价格波动策略与动态回溯机制的蚁群算法
赵家波,游晓明+,刘 升
1.上海工程技术大学 电子电气学院,上海 201620
2.上海工程技术大学 管理学院,上海 201620
旅行商问题(traveling salesman problem,TSP)是一类经典的组合优化问题,可以描述为一位旅行商从某一城市出发,要求不重复通过所有规定的城市,最后回到最初城市的最短路径问题。
在20 世纪90 年代,意大利学者Dorigo、Maniezzo等人受到自然界蚂蚁觅食的启发,模拟蚂蚁觅食的行为,提出了蚁群算法(ant colony optimization,ACO),并应用于旅行商的问题与分布式优化问题,取得了较好的结果。之后学者们根据自身研究领域将蚁群算法应用于配电网故障定位、火力分配问题、网络路由问题、车间调度问题等。
由于信息素的正反馈作用,蚂蚁系统在后期常常因为个别路径信息素的快速积累导致蚂蚁不会选择其他路径,从而陷入局部最优问题。为了避免信息素的过度积累,减少陷入局部最优的概率,Dorigo在蚂蚁系统(ant system,AS)算法的基础上提出蚁群系统(ant colony system,ACS)算法,并提出了全局信息素更新方式与局部信息素更新方式,加入局部搜索算法,改善了算法陷入局部最优的情况。之后,为了避免信息素过多而导致陷入局部最优,Stutzle 等人提出了最大-最小蚂蚁系统(max-min ant system,MMAS),通过分别设置信息素最大最小阈值,将信息素的浓度控制在一定范围内,从而避免信息素的不断堆积造成局部最优。以上是经典的蚁群算法,虽然它们具有高效的探索寻优能力,但仍存在着容易陷入局部最优、收敛速度慢等问题。针对这些问题,许多学者提出各自的改进策略。
一些学者在加快蚁群算法的收敛速度上做出一些改进,如文献[9]结合遗传算法,提出使用蚂蚁的基因控制蚂蚁选择城市,减少算法初期探索全部路径的时间成本,加快算法前期收敛速度。文献[10]通过全局路径重新设定初始信息素分布,使得算法前期路径的探索具有一定导向性,并且通过信息素的二次挥发,加快算法后期的收敛能力,使算法能够在较短时间内找到较优解。文献[11]提出一种改进的信息素差异化更新策略,在所有蚂蚁完成本次路径构建后,对优于平均路径长度的路径进行信息素加强,对劣于平均路径长度的路径进行信息素削弱,从而增大较优路径的吸引力,削弱较差路径对蚂蚁路径选择的干扰,加快算法整体的收敛速度。上述学者较好地解决了蚁群算法收敛速度慢的问题,但算法仍存在易陷入局部最优的问题。文献[12]提出一种具有记忆特征的区间蚁群优化算法,将信息素浓度推广为一定区间范围,不再束缚于信息素为某一定值,并引入长短时记忆的信息素更新方式,对应不同的挥发系数,使得算法呈现更具层次的多样性。文献[13]为了解决算法陷入局部最优的问题,使用平滑信息素的方法削弱所有路径信息素的差异性,并通过自适应改变算法的取值,增大算法接受随机解的概率,从而实现跳出局部最优。文献[14]根据蚁群算法与鱼群算法的优势互补,提出一种先鱼群再蚁群的混合算法,通过更新率的调整,前期借助鱼群算法找到更多的解,当更新率达到某一值时,转为蚁群算法进行更好的寻优,当算法陷入局部最优时,再通过更新率的变化转为鱼群算法,从而平衡收敛速度慢、易陷入局部最优等问题。虽然以上改进的蚁群算法都从加快收敛速度与提高多样性进行改善,但在解决中大规模的TSP 问题中仍然存在收敛速度慢且容易陷入局部最优等问题。
为了在中大规模TSP 问题中较好地平衡解的多样性与收敛速度的关系,本文提出一种结合价格波动策略与动态回溯的蚁群算法(ant colony algorithm based on price fluctuation strategy and dynamic backtracking mechanism,PBACO)。在价格波动策略中,结合时间序列思想将蚁群算法完整迭代周期根据不同需求分为三类,并根据价格波动平衡,将影响价格波动的供求关系进行匹配,通过分析算法在各类时期的不同需求,对信息素挥发因子进行自适应动态供给,来满足算法各阶段的动态需求,较好地改善算法整体性能。当价格波动策略的供给关系无法实现平衡时,算法将面临局部最优问题,此时引入动态回溯机制,以迭代最优蚂蚁的个体相似度作为标准,将路径信息素回溯至相似度差异显著的时期,而非将路径信息素清零,保证了算法收敛速度的同时能够有效跳出局部最优。通过MATLAB 对TSP 中的不同测试集进行仿真,结果表明该算法在保证收敛速度的基础上,有效提高了解的质量,较好地平衡了多样性与收敛速度的关系。本文的主要工作总结如下:
(1)结合时间序列的思想,将蚁群算法完整迭代周期根据不同内在需求分为A、B、C 三类,并采用价格波动策略对三类不同时期的不同需求,自适应调整信息素挥发因子进行动态供给,使算法能够在不同时期对多样性差与收敛速度慢的问题做出相应的改善,优于传统算法恒定的信息素挥发因子。
(2)通过分析三类不同时期的陷入局部最优情况,引入斐波那契数列抽样来判定算法是否陷入局部最优,而非传统算法逐个判断若干代最短路径均不变的方法。采用斐波那契数列抽样的方式通过抽样更少样本数来判定陷入局部最优,节约时间成本,同时对不同时期采用不同的最大样本数,更为合理地进行抽样样本数的调整,进一步加快算法收敛速度。
(3)在算法陷入局部最优后,最优路径信息素积累较多,此时引入动态回溯机制,以迭代最优蚂蚁的个体相似度作为标准,将路径信息素回溯至相似度差异显著的时期,可以将路径信息素重置为若干代前的路径信息素,这样既增加了下代蚂蚁选择路径的多样性,同时未完全重置信息素,节省了蚂蚁重新构建路径信息素的时间成本,在保证收敛速度的同时能够有效跳出局部最优。
1 相关工作
1.1 ACS 蚁群算法1.1.1 路径构建
ACS 中每只蚂蚁从城市到城市的选择公式:

其中,τ()代表着时刻城市和城市之间的信息素的浓度大小,每条边上的起始浓度都是相同的,记为。 η代表的是、城市之间距离d的倒数,即η=1/d。是在区间[0,1]的常数值,是在区间[0,1]的随机数,∈表示城市属于禁忌表外的可选城市集合。表示当≤时将要被选择的下一个城市。是式(2)轮盘赌的选择方式。、分别表示信息启发式因子和期望启发式因子,越大,表示对下一条路径选择受启发式信息素的影响越大,而值越大,表示对下一条路径选择受城市间距离的影响越大。
式(1)、式(2)表明,当≤时,城市之间信息素高的城市和距离相对近的城市被选择的概率更大,当不符合上述条件,采用式(2)轮盘赌进行路径构建。
ACS 蚁群算法的更新机制分为局部信息素更新和全局信息素更新两部分。
全局信息素更新:当所有蚂蚁都完成一次迭代之后,算法只对当前最优路径上的信息素进行更新,通过算法的正反馈作用,使得最优路径和非最优路径上的信息素的差距逐渐拉大,为蚁群的路径选择增加指向性,加快了算法的收敛速度。公式如下:

其中,是全局信息素的蒸发率;Δτ是信息素增量;是当前最优路径长度。
局部信息素更新:当每只蚂蚁完成一次周游后,算法便会对其走过的路径进行局部信息素更新。局部信息素更新是对所有蚂蚁都进行更新,其作用是为了缩短最优路径和非最优路径之间信息素的差距,增加算法的多样性,提高算法全局搜索能力,避免陷入局部最优。公式如下:
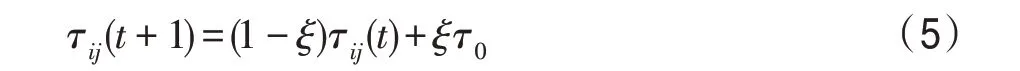
其中,Δτ是信息素增量;为每条边上的起始浓度;是局部信息素的蒸发率。
1.2 时间序列分析法
时间序列分析法是统计学中常用于预测未来发展变化趋势的一种方法,能够以时间的推移预测市场需求趋势,通过将经济跌涨、购买力大小、价格变动等同一常数的观察值,按照时间顺序进行排列,再运用数理统计方法对市场未来趋势的变化进行预测,来确定市场的预测值。
一个时间序列通常由四种要素组成:长期趋势变动、季节变动、循环变动和不规则变动。长期趋势变动是指时间序列在长时期内呈现出来的持续向上或持续向下的变动;季节变动是指时间序列在随季节而重复出现的周期性波动,受气候条件、节假日等各种因素的影响;循环变动是指时间序列变化为非固定时长的周期性波动,其循环周期与趋势不同,它并非是单一方向的长时变化,而是涨落有序的交替波动;不规则变动是指时间序列中除去以上三种要素所剩余的变动,通常随机出现在时间序列中,使时间序列产生不平稳的震荡波动。
时间序列函数可由以上四种元素进行表示,即=(,,,),常用所构建的模型可分为两种,加法模型=+++以及乘法模型=***。当时间序列随时间等宽推进时,常用加法模型;当时间序列的季节变动与长期趋势变动成正比时,常用乘法模型。
1.3 个体相似度
在相似度算法的距离度量中,距离越近则两者差异性较小,证明其相似度越高。但是这类相似度无法直接应用于蚁群算法中,因为当蚁群算法陷入局部最优时,其最优路径基本保持不变,前后两次路径的差异性较小,相似度高,但是对于需要跳出局部最优的问题并非一个好的结果。
考虑到蚂蚁个体在寻找路径时是通过城市节点的连接来进行路径寻优,个体之间形成的闭环路径总会有一些相同路径,因此可用个体间的相同路径信息来表示个体之间的相似度,路径信息相同数越多,则代表个体间的相似度越高,而相同数越少,也表示个体间差异性较为明显。个体相似度的计算过程如下所示。
个体相似度的计算通过相同路径的多少来进行,设两个个体和,其路径信息借助连接矩阵表示,如对应连接矩阵,对应连接矩阵,则有:

其中,代表城市数,在矩阵中,x表示城市至城市的路径信息,如果个体的路径信息中具有城市至城市,则使x=1,否则x=0;因为x与x均表示城市至城市的路径信息,所以x=x,为对称矩阵,个体的连接矩阵同理所示。
个体相似度借助连接矩阵则可以较为明显地比较两个个体的路径信息。在算法运行初期,从随机城市出发的两个蚂蚁个体可能走过完全不同的路径,此时两者的相似度应为0,在算法陷入局部最优或算法运行末期,因为信息素正反馈的作用,两个蚂蚁个体走过的路径可能大体相同,此时两者的相似度为1 或近似为1,所以可构建个体相似度函数,将两个个体的相同路径进行统计处理,使个体间的相似度处于0~1 的范围。个体相似度函数的公式如下所示:
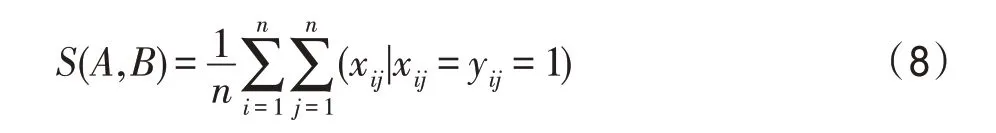
2 改进的蚁群算法
2.1 价格波动策略
价格波动策略结合了价格理论中商品的供求关系对价格的影响,在不同时期商品的价格会受供给和需求的不同而产生变化,但总体价格呈现出波动平衡的状态。而传统蚁群算法在进行路径探索时,存在易陷入局部最优、收敛速度慢等问题,虽然后续提出信息素挥发因子来避免信息素过度积累,改善解的质量,但传统蚁群算法的信息素挥发因子仍具有一定的局限性,信息素挥发因子作为蚁群算法的重要参数,设置为某一定值无法发挥其在算法各阶段的不同作用,对算法整体的适应性较差,因此提出价格波动策略,使算法不同时期的供求关系处于动态平衡状态。
时间序列分析法处理的数据通常是根据时间排列的数据,用来进行曲线的预测与内在发展趋势的变化,本文通过将时间序列思想引入蚁群算法,对蚁群算法各时期的不同状态进行分析分类,为2.1.2 小节价格波动策略的供求关系匹配奠定基础。
下面将通过分析最短路径收敛图来对蚁群算法各时期的不同状态进行分类,为了提高此分类方法的普适性,本文根据文献[7]的ACS 算法,对城市集eil51、eil76、KroA100、KroB100、ch130、ch150、KroA200 和KroB200 进行15 次独立实验,获取各城市集的最短路径收敛图。为了增强说服力,选取各城市集15 次实验中的最优路径收敛图作为典型进行分析。
如图1 所示,蚁群算法的收敛曲线是以迭代数为时间轴,对本次迭代最优蚂蚁的最短距离进行统计,从而绘制成的曲线,因此曲线不会出现往上回升的变化,只存在下降与持平的情况。考虑到以上原因在蚁群算法的特殊性,蚁群算法最短路径的变化曲线在结合时间序列思想时会对曲线的要素做出相应调整,构建符合蚁群算法逻辑的模型。
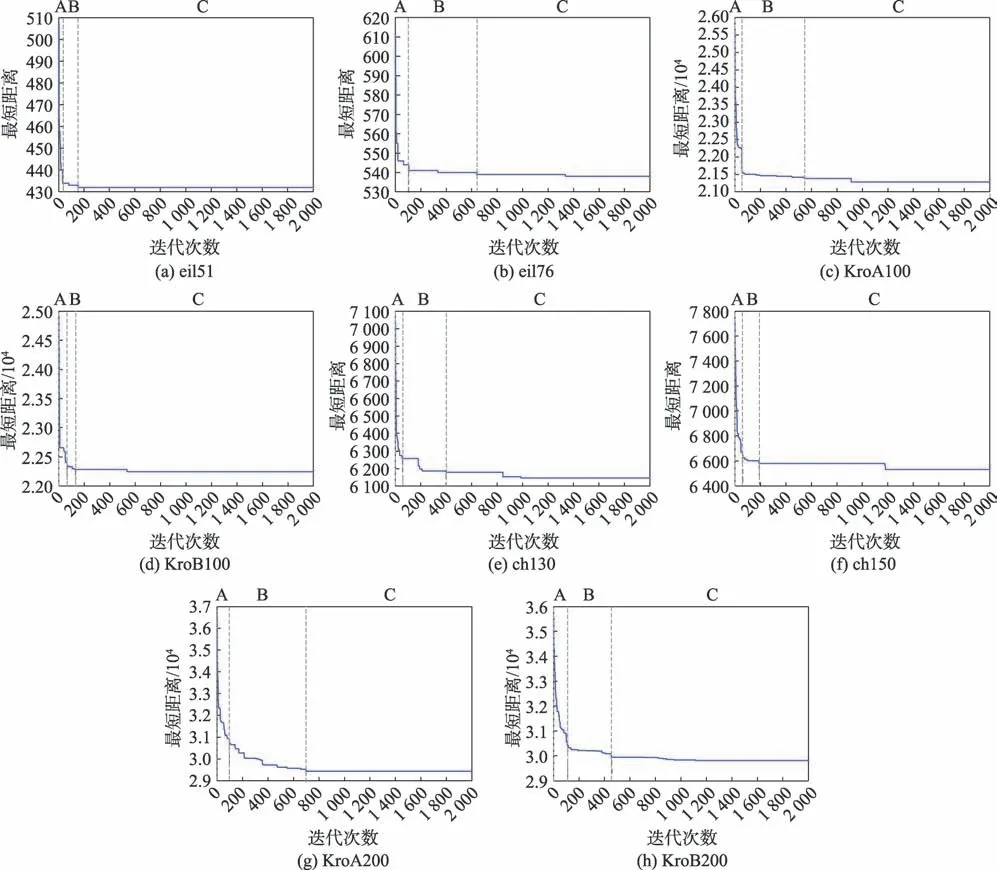
图1 最短路径收敛图Fig.1 Shortest path convergence graph
图1 将根据算法不同时期的不同变化对对应时期的曲线进行要素分类。在图1 中,各城市集的最短路径曲线都可分为A、B 和C 三个阶段。在A 阶段,各城市集曲线呈极速下降趋势,阶段特征为曲线在较少迭代数内落差明显,此时处于算法前期,蚂蚁主要受期望启发式的影响积极探索路径,称之为极速下降变化;在B 阶段,各城市集曲线呈阶梯下降趋势,阶段特征为曲线在持平较短迭代数后发生下降变化,之后再次持平与下降,循环进行,此时处于算法前中期,路径信息素积累至一定程度,蚂蚁的路径选择受启发式与信息素浓度的共同作用,波折探索更短路径,称之为阶梯下降变化;在C 阶段,各城市集曲线呈长期持平或长期持平后下降趋势,阶段特征为曲线在较长迭代数内持平,或在较长迭代数内持平后出现下降,此时处于算法中后期,信息素的正反馈积累使当前最优路径的信息素达到较大值,陷入局部最优,算法只能通过轮盘赌的小概率来寻找更短路径,因此曲线在较长迭代数保持持平,若能找出更短路径,即出现下降现象,称之为恒定兼随机变化。
因为最优路径曲线是以每代进行统计,以上四种分类满足时间序列加法模型,所以可以构建价格波动策略分类模型,如式(9)所示。

其中,为最短路径收敛曲线中的极速下降变化,为极速下降的时长,该时段算法多样性较好,容易找出更优解;为最短路径收敛曲线中的阶梯下降变化,为阶梯下降的时长,该时段信息启发式与期望启发式共同作用,算法多样性逐渐降低,开始陷入局部最优,又跳出局部最优的阶段;为恒定兼随机变化,为恒定兼随机变化的时长,该时期算法的多样性较低,已经陷入局部最优问题,若能跳出局部最优,则为随机变化,若未能跳出局部最优,则为长期恒定变化;为完整收敛曲线,为各阶段时长的总和。
上述通过结合时间序列的思想,分析了蚁群算法最短路径的变化曲线,将蚁群算法迭代周期分为三种阶段时期,在不同时期算法具有不同的需求,而当信息素挥发算子设置为定值时,无法动态调整信息素在各个阶段发挥不同的作用,对算法整体的适应性较差。因此本文提出一种价格波动策略,将影响价格波动的供求关系进行匹配,对信息素挥发因子进行动态调整,用于全局信息素更新公式中,来平衡算法各阶段不同时期的需求。
在算法运行前期,即A 阶段,最优路径曲线处于极速下降变化阶段,此时路径信息素积累量较少,此时若将信息素挥发因子设定为较大值,虽然会削弱正反馈的作用,但此时算法会将期望启发式因子作为主导地位,从而使蚂蚁容易聚集在期望启发式因子最强的路径,变为类贪心算法,容易陷入局部最优;而将信息素挥发算子设为较小值时,有助于加快算法前期的收敛速度,因此在算法前期设置信息素挥发因子为较小值。在算法运行前中期,即B 阶段,最优路径曲线呈阶梯下降阶段,路径信息素积累较为密集,易陷入局部最优,此时采用较大值的信息素挥发因子,来平衡最优路径与其他路径的差异性,使蚂蚁选择其他路径的可能性增大,从而增加探索更优解的概率。在算法运行中后期,即C 阶段,最优路径曲线呈恒定兼随机变化,算法跳出局部最优能力较弱,并在当前最优解上浪费了大量时间成本,因此此时应适当增加算法的收敛速度,应减小信息素挥发因子,以实现算法后期的快速收敛。
综合上述分析,并结合MMAS 的范围限制思想,本文构建一种服从高斯分布的自适应信息素挥发因子。

图2 全局信息素挥发因子Fig.2 Global pheromone volatilization factor
由图2 可知,在算法前期的A 阶段,服从高斯分布的自适应信息素挥发因子将处于较小值,满足算法前期信息素挥发因子较小的需求;当算法运行至中前期的B 阶段,此时算法路径信息素积累逐渐密集,且随迭代数的增加与解的精度的提高,算法陷入局部最优后再跳出局部最优的能力逐渐减弱,此时需要信息素挥发因子也随之增加,而服从高斯分布的自适应信息素挥发因子随迭代数增加而增加,满足此阶段的需求;在算法中后期的C 阶段,最优路径信息素的积累达到较大值,随迭代数的增加与信息素的积累,算法跳出局部最优的概率逐渐降低,此时算法会在当前最优解上浪费大量的时间成本,此时服从高斯分布的信息素挥发因子随迭代数逐步减小,提升算法后期的收敛速度,满足此阶段的需求。
服从高斯分布的自适应信息素挥发因子公式如下所示:

全局信息素更新公式为:

其中,是位置参数,这里设定为1 000;>0 是尺度参数;是调整倍数。通过调整和的值,使信息素挥发因子范围保持在图中各分布区间,对于具体参数选择,在后续实验中会进行分析对比,选出一组相对较好的参数。
2.2 动态回溯机制
动态回溯思想受中值法与最优化估计算法启发,在进行优化计算时通过取区间中值来对最优解不断逼近,当一次中值法结束,对最优解存在区间再次进行中值法,循环往复直至逼近最优解或得到最优解。而在蚁群算法中,常常会遇到陷入局部最优的问题,导致算法在较优解而非最优解浪费大量时间成本,并且解的精度提升较小,因此提出一种动态回溯机制来实现跳出局部最优,改善解的质量。信息素是蚁群算法的核心因素,蚂蚁通过信息素的积累来进行下一个城市的选择,而动态回溯机制正是通过将路径信息素回溯至个体相似度差异显著的时期,此时在未完全陷入局部最优的同时,保留路径信息素的完整性,区别于将信息素初始化的大灾变,节省时间成本,并能有效地跳出局部最优。
动态回溯的核心在于将信息素重置为较优迭代时刻,在判断重置为哪些较优迭代时刻的选择问题上,本文借助个体相似度作为标准,来判断信息素较好的较优时刻,从而进行动态回溯。
该机制首先要对是否陷入局部最优进行判断,传统判断局部最优方式为若干代的至今最短路径是否均相等,此类判断方法需要在每次迭代结束后将最优路径与若干代前每一代的最优路径进行对比,浪费了时间成本。本文借助斐波那契数列来对陷入局部最优进行判定,通过斐波那契数列的抽样方式,结合价格波动策略不同阶段时期的特殊情况,对算法是否陷入局部最优进行判定,在算法前期的A 阶段,算法基本不会出现陷入局部最优的情况;在算法前中期的B 阶段,算法会在陷入局部持续较短迭代数,再跳出局部,此时斐波那契数列抽样的最大样本数会相应减小;在算法中后期的C 阶段,算法会陷入局部最优,并持续较长迭代数,此时斐波那契数列抽样的最大样本数会相应增加。如图3 所示,对比传统局部最优判定方式,假设样本迭代数为50 代,即连续50 代的最短路径均相等,最短路径不发生变化时,判定算法陷入局部最优;而斐波那契数列抽样的方式,在算法前中期设置最大样本数为30,即可通过抽样第1、2、3、5、8、13 和21 这7 组迭代样本的最短路径进行比较,从而判定算法是否陷入局部最优。在算法中后期适当提高最大样本数,设置最大样本数为50,抽样方式同理。随着斐波那契数列的递进,样本抽样跨度显著提高,可以省去检测大量重复样本的时间。采用斐波那契数列抽样进行局部最优的判定,其优点在于能通过抽样的方式快捷合理地判断是否陷入局部最优,节约时间成本,并结合动态回溯机制实现跳出局部最优,使算法解的精度得到较好的提升。
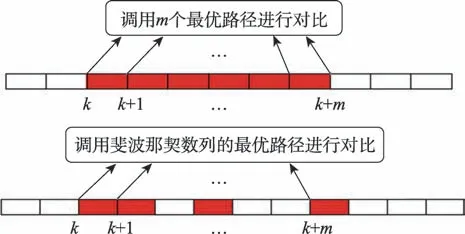
图3 斐波那契数列抽样对比图Fig.3 Comparison chart of Fibonacci sequence sampling
在算法运行时,若出现下一代最优路径与至今最优路径相等,则调用斐波那契数列函数进行判定,设定当前代斐波那契数为1,下一代斐波那契数为2,校验后续满足斐波那契数列代数的最优路径,若经过斐波那契数列抽样后的最优路径都相等,则判定算法陷入局部最优。斐波那契抽样函数公式如下:
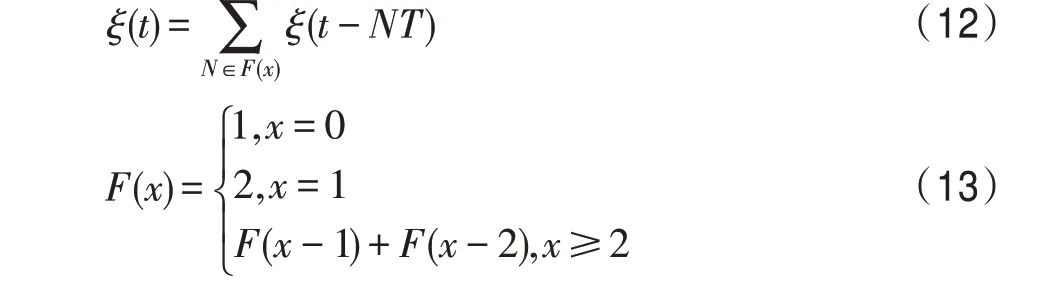
其中,为抽样时刻;=1 为采样周期;()为斐波那契函数;为整数。
若抽样得到的最短路径均相等,则判定算法陷入局部最优,此时对下一代蚂蚁的路径信息素进行回溯,通过式(14)相似度判别公式作为判定条件,回溯到满足此条件且距离当前迭代数最近的较优代,根据式(15)重置其信息素,使其信息素回溯至若干代前个体相似度差异显著的时期,借助此时跳出局部最优能力更强的信息素重新进行路径寻优,迭代代,若仍未跳出局部最优则再次使用式(14),找出满足条件的下一个较优代,再次进行信息素回溯,以此循环直至跳出局部最优或达到迭代最大代数,动态回溯示意图与动态回溯机制流程图如图4、图5 所示。

其中,为个体相似度判定算子,为0 至1 的某一常数。考虑到取1 时,等同于将信息素重置为与至今最优路径相同的路径信息素,并不一定能实现跳出局部最优。为满足相似度判别公式时的迭代数。为信息素回溯后的迭代数,与成正比,当个体相似度高时,回溯的较优代与此时代数相差步长较小,陷入局部最优严重,需要迭代时间加长;反之当个体相似度低时,回溯的较优代与此时代数相差较大,信息素差异明显,此时迭代时间适当缩小。
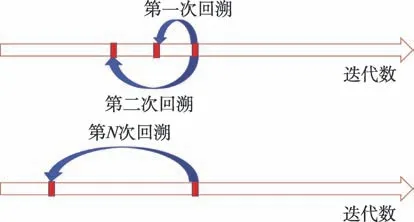
图4 动态回溯示意图Fig.4 Dynamic backtracking diagram
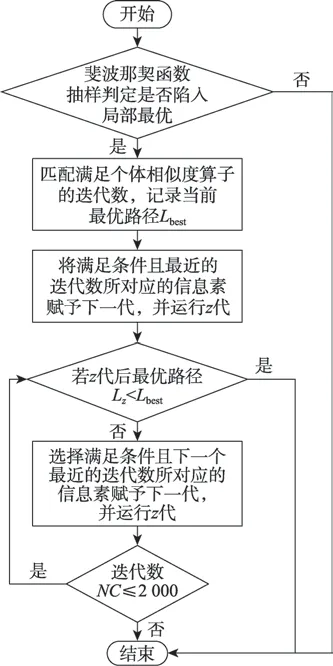
图5 动态回溯机制流程图Fig.5 Flow chart of dynamic backtracking mechanism
当价格波动策略难以通过自适应调整信息素挥发因子来满足算法的需求时,算法陷入局部最优问题,此时将会启用动态回溯机制,使跳出局部最优成为算法的首要任务,通过式(17)强制提升信息素挥发因子,使其达到最大值,来更好地解决跳出局部最优问题。
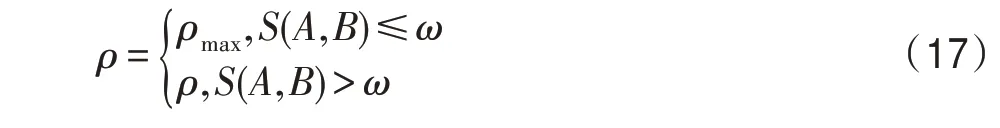
其中,为价格波动策略的最大挥发因子值,当(,)≤时,算法已经陷入局部最优,强制全局信息素挥发因子调整为最大值。
2.3 算法流程
初始化参数,=0。
将只蚂蚁随机分配到各个节点。
根据ACS 算法进行迭代,根据式(10)自适应调整信息素挥发因子,将式(11)作为全局最优更新公式进行信息素更新。
若发现相邻两代最优路径的距离相同,调用斐波那契函数进行抽样,若抽样后的最优路径距离不全部相同,则跳回步骤3;若抽样后的最优路径距离完全相同,则跳到步骤5。
当算法陷入局部最优时,根据式(14)进行动态回溯,匹配满足个体相似度算子的迭代数,记录至今最优路径,根据式(15)将对应的信息素赋予下一代。
以重置后的信息素进行次迭代,若迭代数达到最大迭代时,则找到并输出最优解;若未达到时,则对比当前最优路径与至今最优路径,若当前最优路径小于至今最优路径,则跳出局部最优,跳至步骤7;若不小于至今最优路径,则取满足式(14)的下一个最近迭代数时的信息素回溯,跳回步骤6。
重复上述步骤2~6,直至迭代次,找到并输出最优解。
2.4 算法复杂度分析
虽然本文通过回溯信息素浓度的方式实现跳出局部最优,但并未对迭代总数进行改变。从上述算法流程的分析可以看出,本文算法总的迭代数为,假设算法在第1 代陷入局部最优,动态回溯机制会将若干代前满足相似度标准的该代信息素赋予1代,并运行1 代,若无法跳出局部最优则继续向前寻找满足相似度标准的信息素,赋予第(1+1)代。以此循环,假设迭代数达到代也未能跳出局部最优,则运行总代数为(1+1+2+…+)代,其中=1+1+2+…+;若假设在运行代时实现跳出局部最优,则当前运行代数为(1+1+2+…+),随后运行-(1+1+2+…+)代。综上所述,算法迭代总数仍为,蚂蚁的数量是,城市数为,在每次迭代时因为禁忌表的使用,每只蚂蚁只能搜寻除自身初始城市外的城市,即-1 个城市,因此算法的时间复杂度为(××(-1))即(××),与传统ACS 算法的时间复杂度相同。
3 实验对比与结果分析
为检验PBACO 的算法性能,本文实验使用Windows10 系统,MATLAB2016a 版本的仿真环境,选取国际标准TSP 数据库的多组数据集进行仿真实验。
3.1 节将进行公共参数、价格波动策略与动态回溯机制的参数设置。首先引用文献[7]的公共参数,为了检验后续参数的性能,采用控制变量法,后续全部实验将在统一的公共参数上进行。在设置价格波动策略参数中,以KroA100 作为数据集,将图1 中动态挥发因子的九组不同区间参数,与全局信息素挥发因子为恒定值0.3 时的算法作对比,通过比较30 次独立实验中的最小误差率、满足误差率在0.5%的比例和平均解,来分析挥发因子的动态调整所改善的性能;同时挑出几组较优的区间参数,在A200 数据集上进行30 次独立实验,再次与恒值为0.3 时的算法作对比,通过分析对比更大规模数据集的结果,再次验证算法的改善,并选出一组最佳参数。最后分析动态回溯机制的个体相似度判定因子对性能的影响,综合分析后确定其取值。
3.2 节将进行算法的性能分析,分析不同改进方法的作用。在数据集eil76、KroA150 与tsp225 进行仿真实验,分别对ACS、ACS+波动平衡策略、ACS+波动平衡策略+动态回溯机制进行20 次仿真实验,通过对比实验分析各改进方法的作用及优势。
3.3 节将在多组数据集中对ACS、ACS+3opt 与PBACO 算法进行仿真实验,证明本文算法性能更优,有效改善了蚁群算法解的质量,较好地平衡了解的多样性与收敛速度的关系。
3.4 节将会与其他最新改进算法进行对比分析,再次验证本文改进算法的性能。
3.1 实验参数设置
本文在ACS的基础上进行多次实验,测试了多组参数对算法性能的敏感性作用,统计发现公共参数为表1 所示参数时效果更好。因此,在本文后续实验中,在表1 公共参数不变的基础上测试其他参数,进行敏感性分析。

表1 PBACO 的公共参数设置Table 1 Public parameter setting of PBACO
表1 中,为信息启发因子,影响信息素在路径构建的作用,越小,蚂蚁探索非最优路径的概率增加,解的多样性变好,但容易使期望启发因子作用加强而陷入局部最优;为期望启发因子,越大,蚂蚁选择距离最短路径的概率加大,收敛速度加快,但多样性会降低;为局部信息素挥发率,挥发率过小时,会容易陷入局部最优,挥发率过大时,会影响最优路径的探索;为蚂蚁数量,蚂蚁数量越大,得到的解越多,算法精度相应提升,但会增加时间成本,影响收敛速度;为式(1)的判别阈值,越大,算法探索信息素与距离更短的路径概率越大,收敛速度加快,但多样性降低;为总迭代数。


表2 节点分配组合表Table 2 Node allocation combination table
首先将图2 中的9 组区间参数,与=0.3 在公共参数相同的基础上进行实验对比,在KroA100数据集上进行独立实验30 次,得到的运行结果如表3 所示。
以=0.3 作对比,观察表3 可知,在KroA100 数据集上,各组参数均能找到最优解;在0.1~0.3 区间时,其满足误差率比例与平均解都最优,同时参数为0.1~0.5、0.1~0.9、0.3~0.7 与0.5~0.9 在平均解上都略优于0.3,前三组参数在满足误差率比例上与0.3 持平,虽然0.5~0.9 略低,但在后续仿真时也加入实验,避免遗失潜在优质参数。通过表3 数据可知,价格波动策略在算法各时期对的动态调整,对算法性能具有一定改善作用。
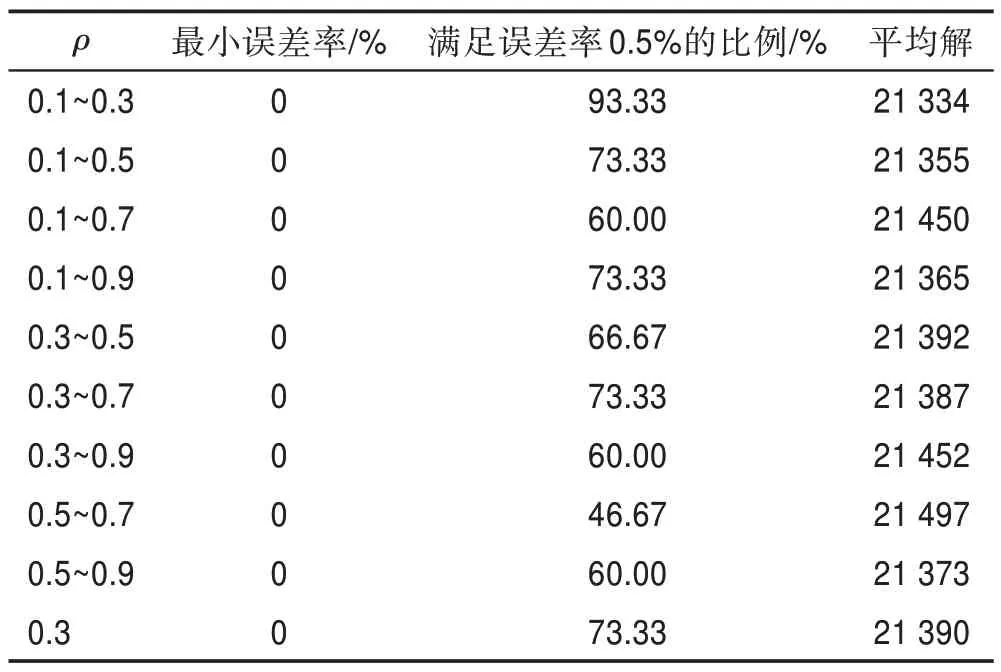
表3 不同区间ρ 在KroA100 对蚁群算法性能的影响Table 3 Effect of different interval ρ in KroA100 on performance of ant colony algorithm
为了确定最佳参数,同时验证算法性能,将以上较优的参数在KroA200 数据集上再次进行独立实验30 次,得到的运行结果如表4 所示。
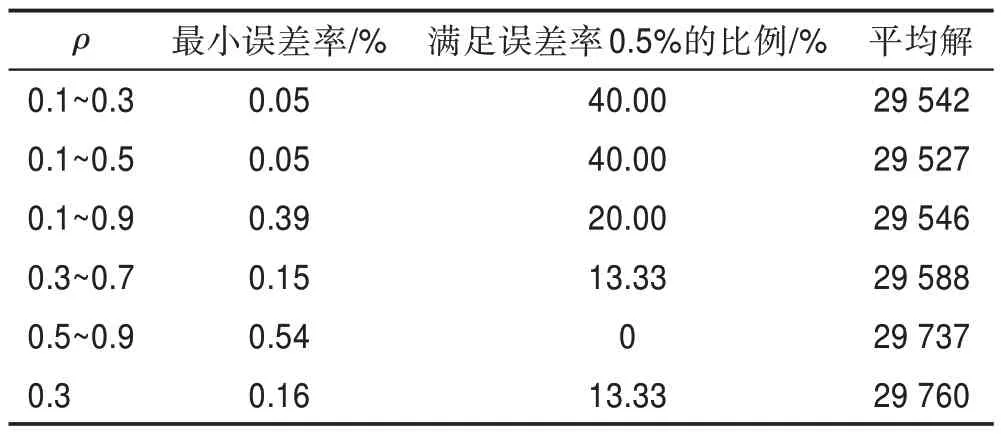
表4 不同区间ρ 在KroA200 对蚁群算法性能的影响Table 4 Effect of different interval ρ in KroA200 on performance of ant colony algorithm
以=0.3 作对比,观察表4 可知,在KroA200 数据集上,参数为0.1~0.3 和0.1~0.5 在最小误差率上最小,能找到精确解的能力优于其余参数,证明此时参数会使解的质量得到提升;在满足误差率比例上,参数为0.1~0.3 和0.1~0.5 均以40%比例高于其他参数,此时参数稳定性能优于其他参数;最后通过比较15组实验最短路径的平均解,发现参数0.1~0.5 的平均解优于参数0.1~0.3,虽然在满足误差率比例上两者持平,但从平均解分析可发现参数0.1~0.5 在解的质量上会略优,因此确定波动平衡策略的参数区间为0.1~0.5,根据式(6),可计算出=577.4,=698.6。
动态回溯机制中参数设置涉及个体相似度判定因子,值越大,个体与最优蚂蚁的路径相似度越高,越难跳出局部最优,值越小,路径差异越明显,但此时也要花费较多的时间成本。综合上述分析并在多组数据集上进行实验,发现在算法陷入局部最优后,回溯至前300 代,个体相似度可降至0.95,回溯至前500 代,个体相似度可降至0.9,再往前回溯虽然个体相似度会较快下降,但其原因是已经贴近初始运行时期,类似于大灾变,因此综合考虑将值设定为0.9。
3.2 算法性能分析
为了验证PBACO 算法各个改进策略的作用,本文将不同策略组合为三组优化方案,分别在数据集eil76、KroA150 与tsp225 进行仿真实验,优化方案如表5 所示。每组优化方案在各数据集进行20 次独立实验,并统计各组方案的最优解、最优解误差率、平均解与迭代次数,并结合收敛曲线与多样性曲线来进行对比与分析,统计结果如表6 和图6 所示。

表5 优化方案表Table 5 Optimization scheme table
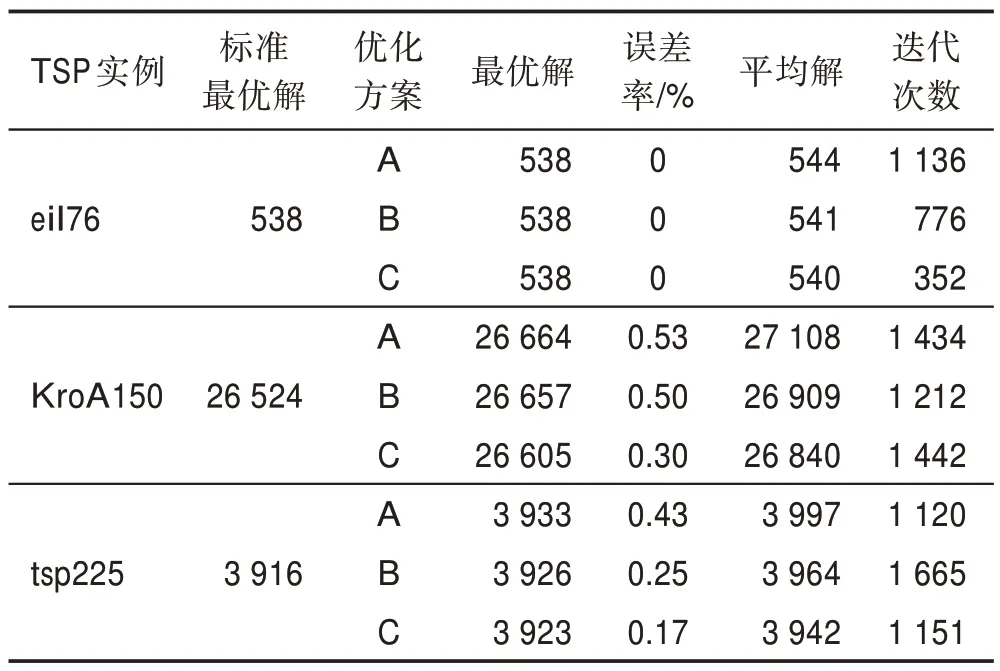
表6 优化方案性能对比表Table 6 Performance comparison table of optimization scheme
从eil76 数据集的实验结果可以发现,A、B、C 方案都可以找到最优解,但是B、C 方案在收敛速度上明显优于ACS 算法,并且更快速地跳出局部最优找到最优解,能够较好地平衡算法多样性与收敛速度,同时从平均解可以看出,改进算法的稳定性也优于ACS 算法。

图6 各测试集收敛情况Fig.6 Convergence of each test set
从KroA150 数据集的实验结果可以发现,在迭代前期,B 方案通过价格波动策略在短时间内就能够找到较优解,优于A 方案,C 方案虽然因为陷入局部最优,未找到较优解,但在300 代左右仍能快速跳出,并找到优于A、B 方案的更优解。在迭代中后期陷入局部最优后,B 方案通过价格波动策略,最先使算法跳出局部最优,但解的精度不高;在此基础上改进的C 方案通过动态回溯机制,进一步跳出局部最优,使算法整体解的精度得到较好的改善。
从tsp225 数据集的实验结果可以发现,B、C 方案在前期收敛速度与探索较优解的能力明显优于A 方案,在中后期的收敛曲线中,C 方案借助动态回溯策略,在更高精度的解中多次跳出局部最优,找到更优解,同时结合表6 中的最优解与平均解可以发现,C方案在解的精度上得到了有效提升,并且相比A、B方案,解的稳定性也得到了明显改善。
3.3 与传统蚁群算法对比分析
为了分析PBACO 算法在不同规模数据集的性能,将ACS、ACS+3opt、PBACO 算法应用于不同城市规模的TSP 实例中,其中ACS 与ACS+3opt 为传统判定局部最优方式,PBACO 算法中的动态回溯机制为斐波那契数列抽样方式判定是否陷入局部最优,结果如表7、图7 和图8 所示。

图7 PBACO 算法在部分城市集最短路径Fig.7 Optimal path of PBACO algorithm for part of city sets
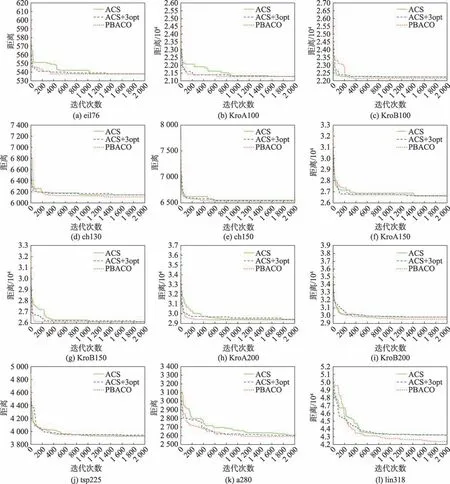
图8 部分城市集收敛情况Fig.8 Convergence for part of city sets
图7 和图8 按顺序分别展示了改进算法在eil76、KroA100、KroB100、ch130、ch150、KroA150、KroB150、KroA200、KroB200、tsp225、a280 和lin318 城市集中的最短路径和收敛情况。从表7、图7 和图8 可以看出,在小规模城市集中,三种算法均能找到最优解,但ACS 与ACS+3opt 的收敛速度明显慢于PBACO 算法,改进算法在前期通过价格波动策略对算法进行改善,能够较快收敛且找到精度较高的解。城市数在100 至200 之间的中规模城市集中,传统算法无法找到ch130 的最优解,而改进算法能通过中后期的动态回溯机制跳出局部最优,找到最优解;对于ch150、KroA150 与KroB150,PBACO 算法相比传统算法均能有效地提高解的精度,并且在KroB150 城市集能精确找到最优解,同时找到最优解的迭代数明显缩减。在城市数大于200 的城市集中,从表7 中可以发现,PBACO 算法在解的精度上得到了较大的改善,并且找到最优解的迭代数也有部分减少,其中KroA200找到贴近最优解的较优解,KroA200 与a280 在改善解的精度的同时将收敛速度提升,虽然在tsp225 城市集中PBACO 迭代数较大,但在动态回溯机制的作用下,多次跳出局部最优,找到更优解。在大规模城市集lin318 中,虽然在迭代前期PBACO 算法陷入短暂的局部最优,但在200 代之后算法解的精度明显提高,在550 代相比传统算法已经找到更优解,并在之后陷入局部最优后,通过动态回溯机制多次跳出局部最优,将解的质量明显改善。

表7 不同规模城市数据集的性能对比Table 7 Performance comparison of urban datasets of different sizes
3.4 与至今最新改进算法对比分析
为了进一步验证PBACO 算法性能,本文选用至今最新改进的融合猫群算法的动态分组蚁群算法(CACS)、考虑动态导向与邻域交互的双蚁型算法(TREEACS)和文献[11]进行比对,如表8 所示。由表8 可以看出,PBACO 算法在小规模城市中与其他算法都能找到最优解,但在中规模城市与大规模城市中,PBACO 算法解的精度相比其他算法得到了较好的改善。
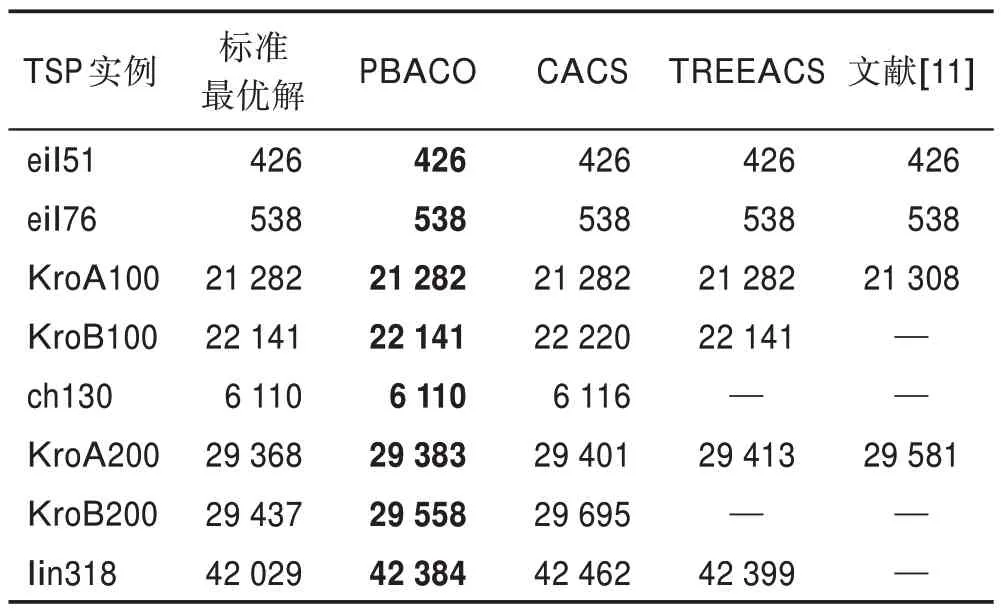
表8 PBACO 与其他最新改进算法比较Table 8 Comparison of PBACO with other newly improved algorithms
通过实验分析与结果对比可知,本文改进后的PBACO 算法与传统蚁群算法ACS、ACS+3opt和至今最新改进的蚁群算法相比,解的精度与收敛性都有明显的改善。
4 结束语
针对传统蚁群算法存在易陷入局部最优、收敛速度较慢等问题,本文提出一种结合价格波动策略与动态回溯机制的蚁群优化算法(PBACO)。通过价格波动策略,以时间序列分析的思想将算法不同需求的时期进行分类,以价格波动平衡的供求思想对信息素挥发因子进行自适应动态供给,在保证收敛速度的同时增大跳出局部最优的能力,能够有效地改善解的质量。在算法陷入局部最优后,引入动态回溯机制,以迭代最优蚂蚁的个体相似度作为标准,将路径信息素回溯至相似度差异显著的时期,在保证收敛速度的同时能够有效地跳出局部最优,明显改善解的精度,并且保证解的稳定性。虽然在实验对比中相较其他算法解的质量得到较好的改善,但在超大规模城市集中算法解的精度还需要进一步提升,因此下一步将进行多种群合作竞争的算法研究,以提高算法在超大规模城市集中的求解能力。

