基于GSA 与DE 优化混合核ELM 的网络异常检测模型

生 龙，袁丽娜，武南南，姬少培

（1.河北工程大学信息与电气工程学院，河北 邯郸 056038；2.河北工程大学河北省安防信息感知与处理重点实验室，河北 邯郸 056038；3.天津大学 智能与计算学部，天津 300072；4.中国电子科技集团公司第三十研究所，成都 610041）

0 概述

随着网络技术的不断发展，特别是Internet 的普及，网络安全问题受到学者的广泛关注。作为一种新的安全防御技术，入侵检测系统（IDS）可以主动保护网络系统免受非法外部攻击。IDS 能够通过检测和响应各种恶意行为来提高系统的可靠性和安全性。文献［1-2］介绍了网络威胁的研究现状，将IDS分为异常检测系统和签名检测系统两类。异常检测系统在检测未知攻击方面表现更好，但是会产生很高的误报率。签名检测系统依靠特定的攻击特征来区分正常活动和恶意活动，但是这些系统的检测效果受到检测规则的直接影响。因此，提高入侵检测系统的检测精度和学习速度仍然是一项艰巨的任务［3］。

当前在入侵检测（ID）领域已经有了大量研究。文献［4］介绍一种有效的异常检测方法，可以从网络流量数据中提取准确的和可解释的模糊规则进行分类。文献［5］将主成分分析（PCA）法用于ID。文献［6-7］介绍了K 最近邻（KNN）方法在恶意攻击检测上的应用，该方法具备高精度和高检测率的特点。文献［8］介绍一种基于贝叶斯理论和决策树的新型多级混合分类器，并将其用于IDS。文献［9］提出一种具有自适应神经模糊推理特征的策略增强模糊模型，该模型以较高的检测精度和较低的误报率来应对与SOAP 相关的攻击。文献［10］提出一种用于自适应入侵检测系统的实时多代理系统的方法（RTMAS-AIDS），该方法允许IDS 进行未知攻击的实时检测，并且应用混合支持向量机（SVM）和极限学习机（ELM）来对正常行为和已知攻击进行分类。文献［11］提出一种基于SVM 算法的入侵检测模型，取得了很好的检测效果。上述研究在检测和报告恶意攻击方面取得了较好的性能，但是在准确率及模型泛化性上仍有待提高。

现有研究旨在提供一种能够准确有效进行网络入侵检测的方法，需针对特定的攻击特征以高精度和快速的学习速度来区分正常活动和恶意活动。文献［12］将粒子群优化（PSO）算法用于SVM-KNN 的参数优化，以构建具有更优准确性的分类器。文献［13］提出一种基于差分进化（DE）的加权SVM 多类分类器。ELM［14］是进行入侵和攻击检测的常用方法。文献［15］提出一种具有高斯核的自适应差分进化极限学习机，用于进行网络入侵检测。PSO 是一种启发式优化方法，需要确定的参数较少，具有收敛速度快和局部优化能力强的优点。文献［16-17］指出DE 算法也是一种启发式优化方法，具有很强的全局优化能力与适应性强的优势。但是PSO 和DE 算法都有其自身的缺点，即前者很容易陷入局部最优，而后者的局部优化能力相对较弱。

本文在上述研究的基础上，将径向基核函数（RBF）与多项式核函数相结合组成混合核函数，构建混合核函数ELM 模型（HKELM），同时将GSA、DE、KPCA 及HKELM 模型相结合，构建基于GSA 与DE 优化HKELM 的网络入侵检测模型KPCAGSADE-HKELM。

1 混合核函数ELM 模型

1.1 ELM 模型

极限学习机（ELM）最初针对单隐层前馈神经网络进行训练，具有学习速度快、泛化能力强的特点［18］。

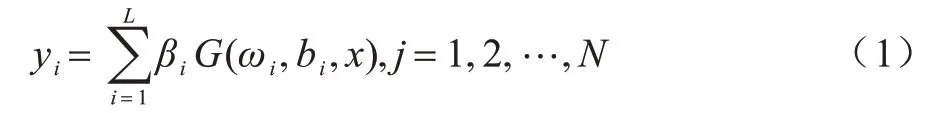
可简写为：

其中：H为ELM 的隐含层输出矩阵；Y∈RN×m为期望输出向量；输出矩阵β∈，为隐含层单元个数。

模型对参数ωi和bi进行随机赋值，即可得出输出矩阵：

其中：H†为H的广义逆。

1.2 HKELM 模型

虽然ELM 模型具有较好的泛化性能，但是将模型应用于几个未知的测试数据集时，ELM 模型的预测准确性可能会相对较低。2012 年，HUANG 等［19］为提高模型的泛化能力，将核参数I/C引入到HHT中，这一ELM 模型即核函数极限学习机（KELM）。KELM 的输出函数如下：

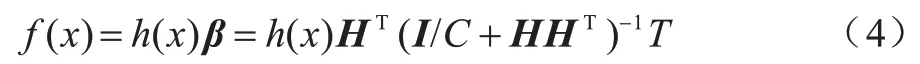
其中：常数C是惩罚参数；I是单位矩阵。

KELM 核函数的定义如下：

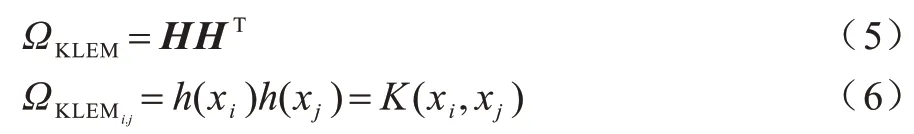
核函数的选择会极大地影响KELM 模型的性能。因此，为KELM 模型找到合适的核函数具有重要意义。多项式核函数是典型的全局核函数，其对应的KELM 模型具有较强的泛化能力和较弱的学习能力［20-21］。径向基核函数RBF 是典型的局部核函数，这意味着相应的KELM 模型具有很强的学习能力和弱泛化能力［20-21］。多项式核函数的泛化能力优于RBF 核功能，而学习能力较差。因此，为了提高KELM 的通用性和学习能力，本文将两个核函数相结合组建新的混合核函数作为KELM 的核函数，此时的KELM 模型即为混合核函数ELM（HKELM）模型。混合核函数的计算公式如下：

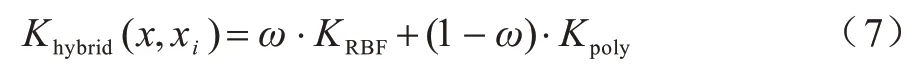
其中：常数ω是混合核函数的权重系数，ω∈[0，1]；Kpoly(x，xi)=(x·xi+b)p代表多项式核函数，b和p分别为常数和多项式核函数的指数参数；KRBF(x，xi)=代表径向基核函数，σ是径向基核函数的指数参数。

2 结合GSA 的差分进化算法

2.1 引力搜索算法

引力搜索算法（Gravitational Search Algorithm，GSA）是ESMAT 提出的一种群智能优化算法，其以万有引力与牛顿第二定律为基础［22］。

GSA 中第i个粒子的质量Mi(t)的计算公式如下：

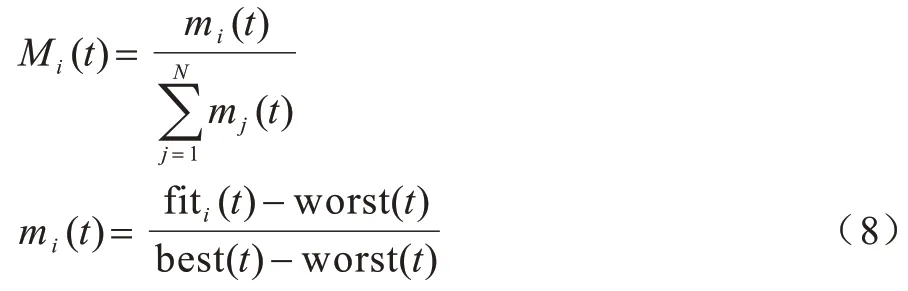
其中：N为粒子的总数；fiti(t)为第i个粒子在t次迭代的适应度；best(t)和worst(t)分别为迭代时所有粒子最好和最差的适应度；mi(t)计算粒子的质量，为第i个粒子相对于迭代中最好和最差适应度的比值［22］，具体如下：

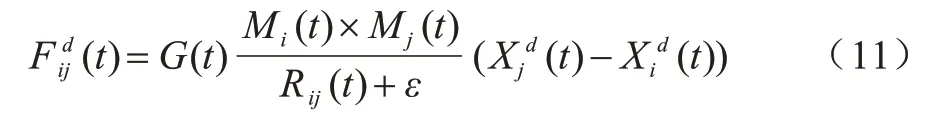
其中：Rij(t)为粒子间的欧氏距离；ε是保证分母不为0 的常量；是第t次迭代时第i个粒子在第d维的位置。

随着迭代次数的增加，引力常数G(t)的值逐渐减小，表示为：

其中：G0为初始引力；T为最大迭代次数；α为衰减系数。

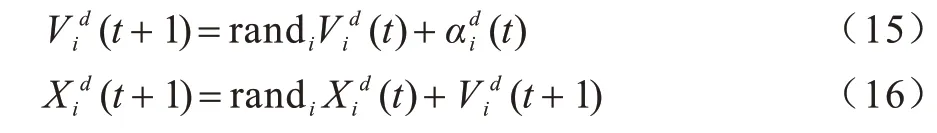
算法的最优解为反复迭代直至满足终止条件后粒子的位置。

2.2 差分进化算法

差分进化（Differential Evolution，DE）算法是一种基于种群进化的智能优化算法［23］。

假设进化代数T，种群规模NP，解空间维度D，第T代的种群个体vi，T=(xi1，T，xi2，T，…，xiD，T)。标准DE 算法步骤如下：

步骤1初始化种群。一般采用随机初始化种群策略。

步骤2变异操作。变异操作是DE 算法的核心内容，常用的变异策略为：

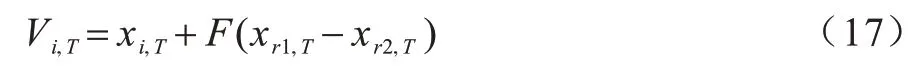
其中：Vi，T为第i个变异个体；xi，T为第i个父代个体；xr1，T和xr2，T是父代中2 个互不相同且不同于xi，T的个体；F为变异率。

步骤3交叉操作。交叉操作能增加种群多样性，其表达式为：

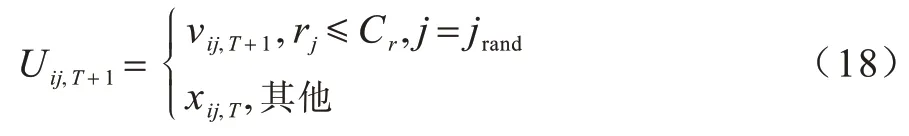
其中：Uij，T+1为实验个体；Cr为交叉率；rj为在［0，1］区间的随机数；jrand∈[1，2，…，D]为随机选择的一个整数。

步骤4选择操作。选择操作通过比较父代个体和子代个体的目标函数值来选择更优的个体，其表达式为：

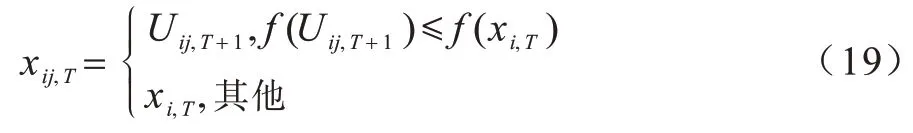
其中：f(·)为适应度值。

计算公式如下：

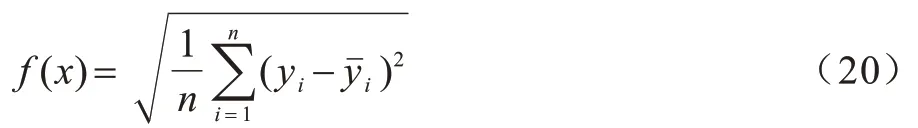
其中：yi和分别是实际结果和预测结果。

2.3 差分进化算法

DE 算法的全局优化能力很强，可以利用差分信息准确地找到搜索空间的全局最优值，然而其局部优化能力相对较弱［24］。GSA 的局部优化能力较强，而其全局优化能力相对较弱。因此，本文将GSA 和DE 算法相结合，提出结合GSA 的差分进化算法（GSADE）。

GSADE 算法流程如图1 所示。

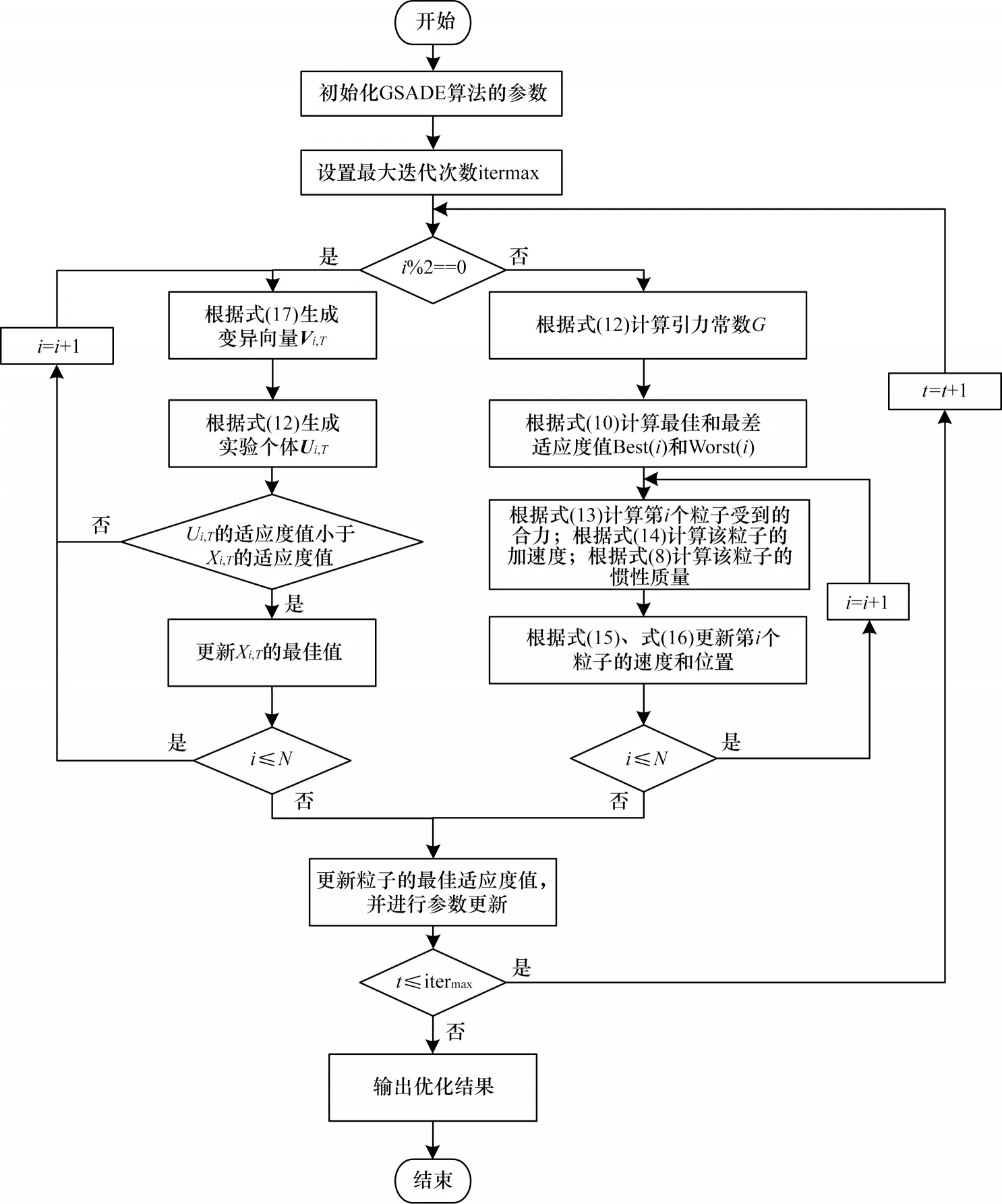
图1 GSADE 算法流程Fig.1 Procedure of GSADE algorithm

GSADE 算法的运行步骤如下：

步骤1初始化种群粒子个数N以及粒子的初始速度与位置。初始化GSADE 的参数，包括衰减系数α、初始引力常数G0等。设置算法最大迭代次数为itermax，当前迭代次数为t。

步骤2根据式（20）计算适应度值。

步骤3如果迭代次数t为奇数，则运行步骤4；否则跳转到步骤5。

步骤4运行GSA 算法：

1）根据式（12）计算引力常数G；

2）对于求解最小问题，根据式（10）计算最佳和最差适应度值best(t)和worst(t)；

3）根据式（13）计算第i个粒子受到的合力；根据式（14）计算该粒子的加速度；根据式（8）计算该粒子的惯性质量Mi(t)；

4）根据式（15）、式（16）更新第i个粒子的速度和位置；

5）如果i≤N，则返回步骤3）；否则跳转到步骤6。

步骤5运行DE 算法：

1）根据式（17）生成变异向量Vi，T；

2）根据式（18）生成实验个体Uij，T+1；

3）如果fiti(Uij，T+1)≤fiti(xi，T)，则运行步骤4）；否则跳转到步骤1）；

4）如果i≤N，则返回步骤1）；否则，转到步骤6。

步骤6根据粒子的新适应度值进行参数更新。

步骤7如果t≤itermax，则返回步骤3；否则，转到步骤8。

步骤8输出更新结果作为最优参数。

3 核主成分分析

主成分分析（PCA）是一种用于特征提取和降维的经典方法［25］。KPCA 由SCHOLKOPF 等［26］提出，是对PCA 的改进，可以有效地处理非线性问题。

使用非线性映射函数φ，KPCA 将非线性训练样本X=[X1，X2，…，XN]T∈Rn×d映射到高维特征空间Γ：

通过使用简单的非线性映射函数φ，输入空间中不可分割的数据在高维特征空间Γ中变得可分离，然后利用PCA 方法提取Γ中的特征，实现了非线性训练样本的特征提取。

4 基于GSA 与DE 优化混合核ELM 的网络入侵检测模型

本文基于上述研究，提出一种新型的网络入侵检测模型——基于GSA 与DE 优化混合核ELM 的网络入侵检测模型（KPCA-GSADE-HKELM）。该模型的具体步骤如下：

步骤1输入数据集及KPCA-GSADE-HKELM模型的初始参数。

步骤2使用KPCA 方法对输入数据集进行降维和特征提取。

步骤3运用预处理的训练数据集训练HKELM模型；使用GSADE算法优化HKELM 的模型参数，当迭代次数达到最大值itermax时，优化过程停止，获得最佳参数。

步骤4使用测试数据集评估获得的最佳HKELM 模型的性能。

步骤5输出模型检测结果的评估指标。

基于KPCA-GSADE-HKELM 模型的网络入侵检测流程如图2 所示。

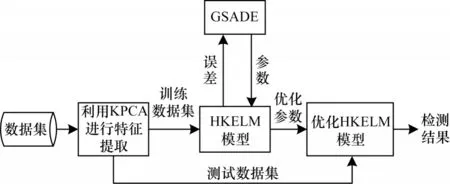
图2 基于KPCA-GSADE-HKELM 模型的网络入侵检测流程Fig.2 Network intrusion detection procedure based on KPCA-GSADE-HKELM model

5 仿真实验

5.1 实验数据

本文在实验中选择KDD99 数据集进行仿真实验。KDD99 数据集中共包含23 种攻击类型，可以分为四大攻击类别：DoS，PRB，U2R 和R2L［27］。由于利用KDD99 完整的数据集在进行机器学习算法训练时很复杂，因此大多数研究人员都使用了KDD99 数据集10%子集作为实验数据。表1 给出了数据集的详细信息，其中训练数据集和两个测试数据集分别表示为T0、T1 和T2。训练数据集T0 与测试数据集T1 一起用来验证GSADE-HKELM 和 KPCAGSADE-HKELM 模型的有效性。此外，本文还利用测试数据集T2 进行KPCA-GSADE-HKELM 模型与其他研究模型的性能比较。

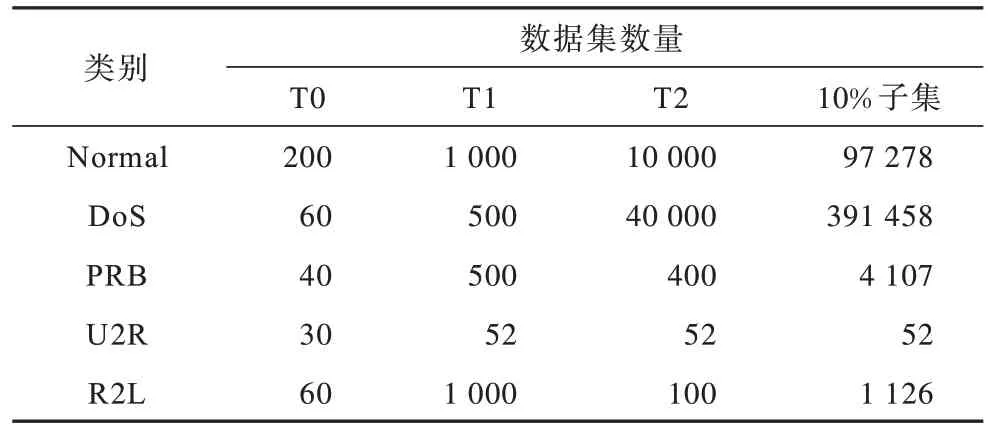
表1 KDD99 数据集详细信息Table 1 Details of KDD99 dataset

5.2 实验结果评价指标

为了评估KPCA-GSADE-HKELM 算法的性能，本文利用python 进行仿真实验分析，采用精准率（Precision）、召回率（Recall）和F-score 值作为每类攻击的评估指标；采用准确率（Accuracy，Acc）、平均准确率（Mean accuracy，MAcc）、平均F-score（Mean Fscore，MF）和假正例率（False Normal Rate，FNR）作为数据集整体的评估指标。表2 为评估指标的详细解释。在数据集中的网络连接可以分为正常（标记为0）、攻击（标记为1，2，…，c−1）两大类，其中c表示网络连接的类别数。

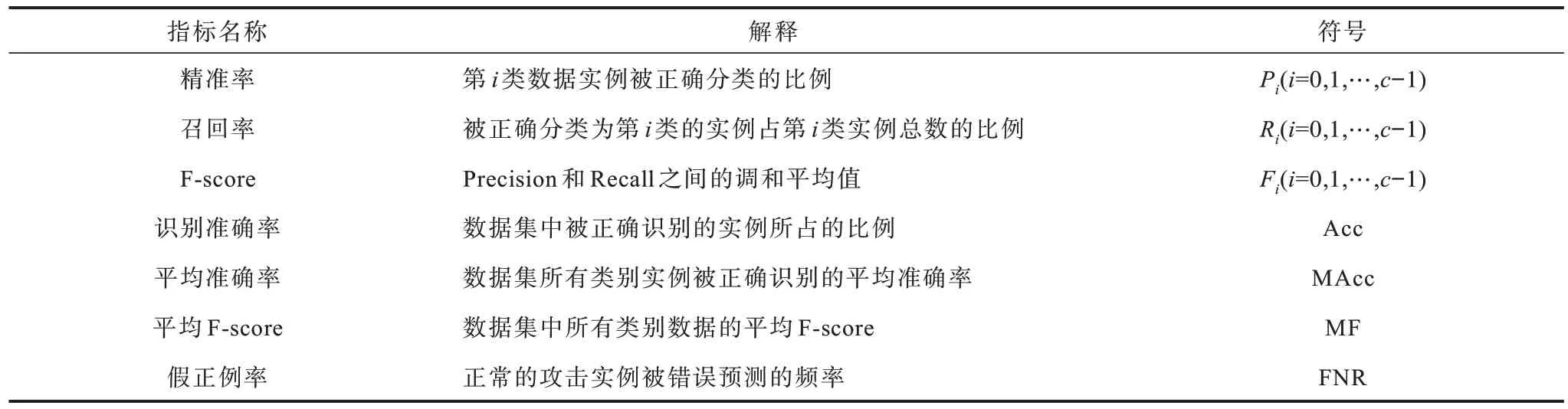
表2 评估指标详细解释Table 2 Detailed explanation of evaluation indicators

5.3 实验结果分析对比

在实验中，本文利用训练数据集T0 和测试数据集T1 进 行GSADE-HKELM 与DE-HKELM、GSAHKELM 模型的性能对比，以及KPCA-GSADEHKELM 模型与GSADE-HKELM 模型的性能对比；最后在数据集T2 上，将KPCA-GSADE-HKELM 方法与其他检测方法分别进行入侵检测。

5.3.1 DE_KELM、GSA_KELM 与GSADE-HKELM模型的对比

由于在对HKELM 进行训练时，通过人工经验很难快速、准确地找到最佳参数值。为此，本文引入了群智能优化算法GSADE，以自适应的方式获得最佳参数值。同时，为验证其效果，将DE-KELM、GSA-ELM 与GSADE-HKELM 模型进行比较。在实验中，DEHKELM 与GSADE-HKELM 中DE 算法的参数设置保持一致，其中种群设置大小NDE设置为20，最大迭代次数itermax设置为100；式（17）中参数F设置为0.8，式（18）中交叉率Cr设置为0.2；GSA-KELM 与GSADEHKELM 中GSA 算法的参数设置保持一致，其中种群大小NGSA设置为20，最大迭代次数itermax设置为100，式（11）中的常数ε设置为2–40，式（12）中的初始重力常数G0设置为250，衰减系数α设置为15。

表3和图3给出了由DE-HKELM、GSA-HKELM和GSADE-HKELM 模型获得的每个类别详细的F-score值。从中可以看出，通过GSADE-HKELM 获得的每个类别的F-score值均高于其他两种方法，尤其是在U2R类数据上。而且，由DE-HKELM 获得的平均F-score值为92.23%，GSA-HKELM 的平均F-score值为93.21%，GSADE-HKELM 的平均F-score值为94.44%。与DEHKELM 和GSA-HKELM 相比，GSADE-HKELM 的平均F-score 值分别提高了约2.11 个百分点和1.23 个百分点。

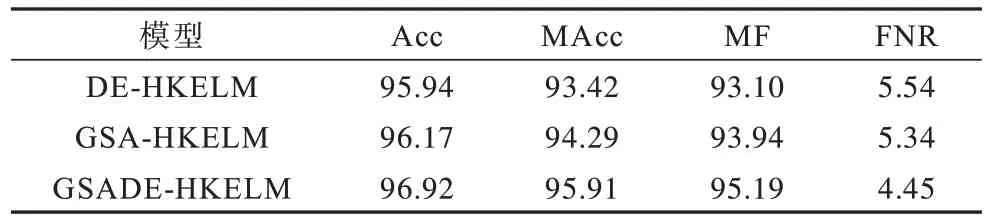
表3 DE-HKELM、GSA-HKELM 和GSADE-HKELM在T1 上获得的每个类别数据的F-score 值Table 3 The F-score value of each category data obtained on T1 by DE-HKELM，GSA-HKELM and GSADE-HKELM %

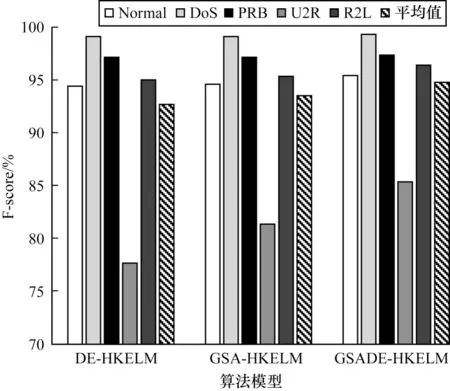
图3 DE-HKELM、GSA-HKELM 和GSADE-HKELM 的F-score 值和平均F-score 值Fig.3 F-score value and average F-score value of DEHKELM，GSA-HKELM and GSADE-HKELM

表4 给出了 DE-HKELM、GSA-HKELM 和GSADE-HKELM 3 种模型在数据集T1 上各种总体评估指标值。GSADE-HKELM 的Acc、MAcc、MF 均明显高于DE-HKELM 和GSA-HKELM，而GSADEHKELM 的FNR 值明显低于其他两种方法。结果表明，混合优化算法GSADE 在确定最佳参数以提高HKELM 性能方面明显优于单DE 和GSA 优化HKELM 模型，将GSA 与DE 算法结合起来进行HKELM 模型的优化时充分发挥了两个算法的优势，克服了两者自身存在的缺陷。

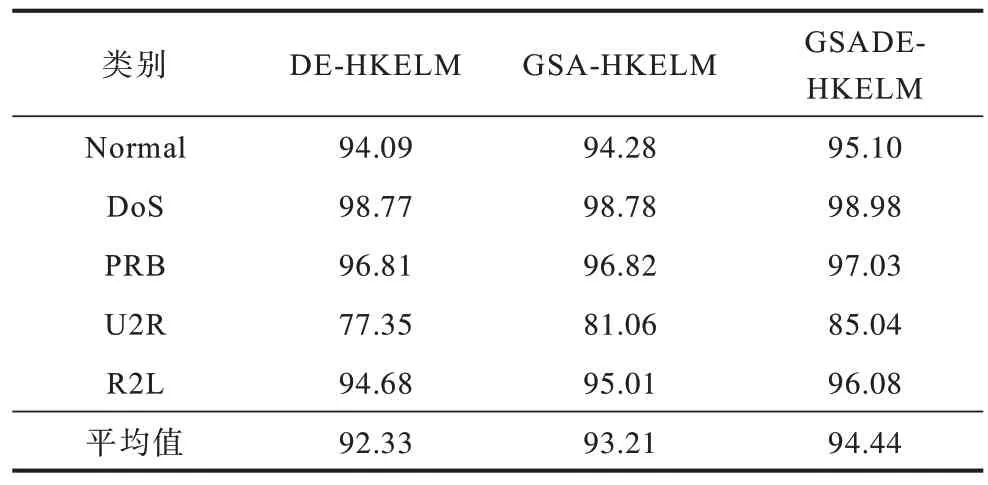
表4 DE-HKELM、GSA-HKELM 和GSADE-HKELM在T1 上的各评估指标Table 4 Various evaluation indicators of DE-HKELM，GSA-HKELM and GSADE-HKELM on T1 %

5.3.2 GSADE-HKELM 与KPCA-GSADE-HKELM的对比

KPCA 算法的引入可以减少不重要的特征对分类结果和计算效率的影响。表5 显示了GSADEHKELM 和KPCA-GSADE-HKELM 在数据集T1 的各种评估指标值。在表5 中，KPCA-GSADEHKELM 的Acc、MAcc、MF 值分别为97.11%、96.08%和94.88%，分别高于GSADE-HKELM 的97.01%、96% 和94.58%。KPCA-GSADE-HKELM 的FNR 为4.15%，与GSADE-HKELM 的4.54% 相比，降低了8.59 个百分点。此外，GSADE-HKELM 的运行时间为0.037 391 s，KPCA-GSADE-HKELM 的 运行时间为0.016 379 s，与GSADEHKELM 相比，KPCAGSADE-HKELM 在时间上降低了56.19%，这表明本文所提出的KPCA-GSADE-HKELM 方法具有更高的计算效率，利用KPCA 首先进行数据集的降维，然后通过GSADE-HKELM 方法进行异常检测时具有更好的检测效果和更高的检测效率。

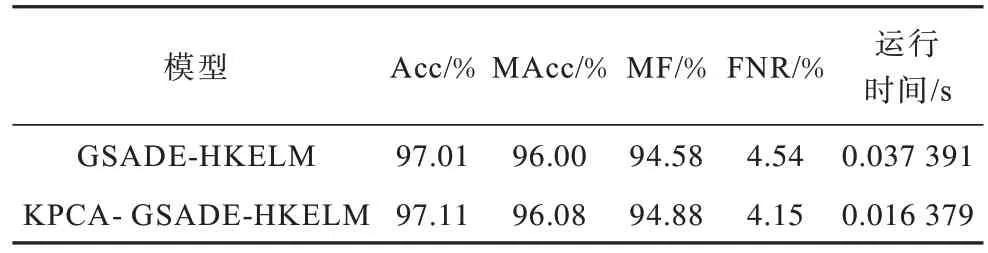
表5 GSADE-HKELM 和KPCA-GSADE-HKELM 在数据集T1 上的评估指标值Table 5 Various evaluation index values of GSADEHKELM and KPCA-GSADE-HKELM on T1

5.3.3 KPCA-GSADE-HKELM 与其他模型的对比

对于本文提出的KPCA-GSADE-HKELM 模型，下面在测试数据集T2上将其与KDDwinner［28］、CSVAC［29］、CPSO-SVM［30］、Dendron［3］分别进行测试，结果如表6 所示。从表6可以看出，与其他模型相比，KPCA-GSADEHKELM 模型在DoS 和U2R 攻击数据上具有更高的分类精度。KPCA-GSADE-HKELM 模型检测结果的评估指标Acc、MAcc和MF 的值分别为98.53%、94.91%和86.74%。KPCA-GSADE-HKELM、KDDwinner、CSVAC、CPSO-SVM、Dendron 模型的MF 值分别为86.74%、59.70%、66.53%、73.42%、84.12%；与KDDwinner、CSVAC、CPSO-SVM 和Dendron 相比，KPCA-GSADEHKELM 模型检测结果的MF 值分别提高了约27.04、20.21、13.32 和2.62 个百分点。这充分说明KPCAGSADE-HKELM 模型在KDD99 数据集上具有更好的性能。

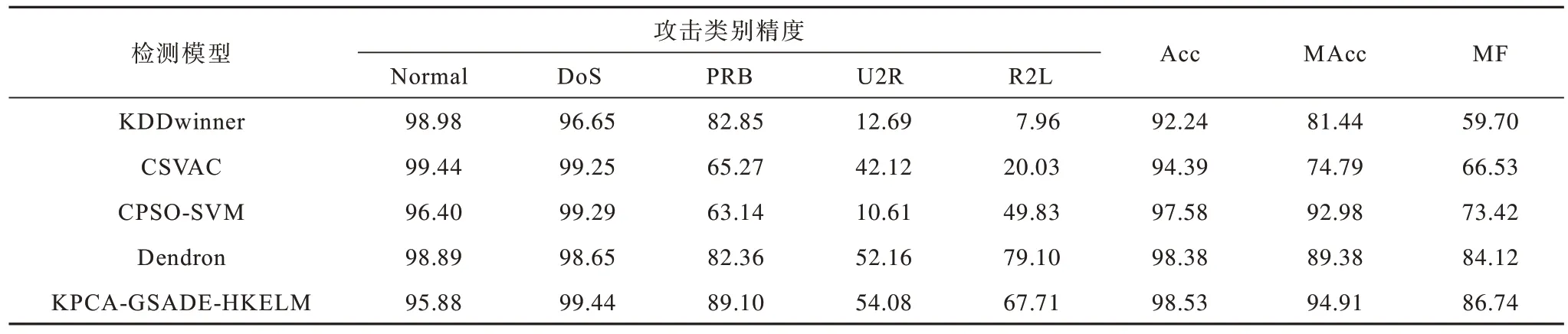
表6 KPCA-GSADE-HKELM 与其他模型在T2 上的检测结果Table 6 Test results of KPCA-GSADE-HKELM and other models on T2 %

6 结束语

本文提出一种基于GSA 与DE 优化混合核ELM的网络入侵检测模型KPCA-GSADE-HKELM。该模型利用能够反映网络流量模式的KDD99 数据集进行模型评估，并将两个核函数相结合构建新的混合核函数HKELM 模型，以提高KELM 的通用性和学习能力。实验结果表明，与KDDwinner、CSVAC、CPSO-SVM、Dendron 等模型相比，KPCA-GSADEHKELM 模型具有更好的检测性能和更高的检测效率。下一步通过将特征嵌入技术与深度学习技术相结合进行网络异常入侵检测［31］，并利用KDD99 数据集及网络流量数据集UNSW-NB15 进行实验，进一步提高网络入侵攻击的检测率。