碳计算和碳管理
近年来,碳排放引起的温室效应等气候问题引起了全世界越来越多的重视。日渐恶劣的气候变化严重危害了生态系统的平衡,对人类活动产生深远的影响。具体表现有我们经常听到的全球气温升高、冰川融化、海平面上升等。此外还如:在一些地区,降水的变化、冰雪的消融改变了当地的水文系统,影响了水源的数量和质量;影响到一些动物的生活习性,改变了它们生活的地理范围、季节性活动、迁移模式、丰富度和物种间的相互作用;对人类农作物生产也产生了很大的影响,危害了粮食安全。事实上,气候变暖不仅只停留在新闻报道和我们的感觉上,而是实实在在地影响甚至是威胁着人类的生存状态。


所谓双碳,是碳达峰与碳中和的简称。
习近平总书记强调指出:“实现碳达峰、碳中和是一场广泛而深刻的经济社会系统性变革。”同时指出:“我们必须深入分析推进碳达峰碳中和工作面临的形势和任务,充分认识实现‘双碳’目标的紧迫性和艰巨性,研究需要做好的重点工作,统一思想和认识,扎扎实实把党中央决策部署落到实处。”
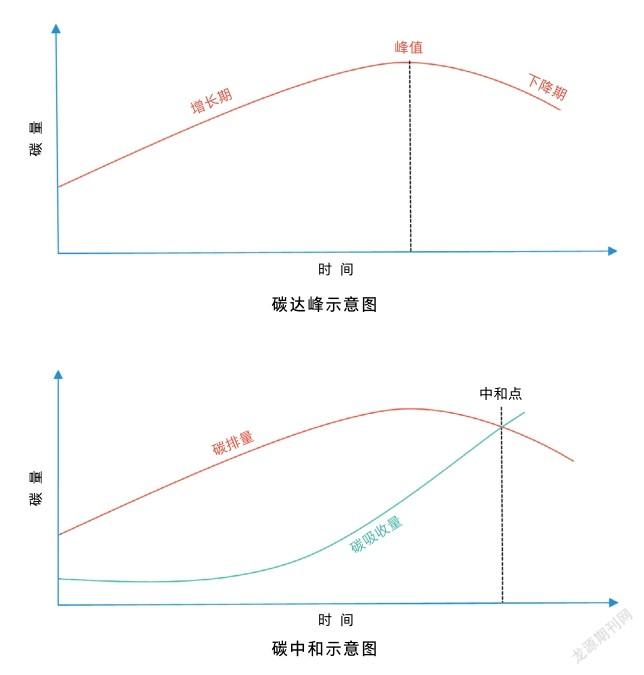
碳达峰指CO2排放量在某一年达到了最大值,之后进入下降阶段。
碳中和则指一段时间内,特定组织或整个社会活动产生的二氧化碳,通过植树造林、海洋吸收、工程封存等自然、人为手段被吸收和抵消掉,实现人类活动二氧化碳相对“零排放”。
可以看到,实际上双碳所涵盖的这两个名词的数学意味很浓。用数学的话说,碳达峰对应的就是微积分中碳排放量关于时间的函数,现在这个函数是增函数,在未来的某时间点将达到最大值,而碳中和就是碳排放中的一正一负两个函数,现在是正大负小,我们需要増负减正,使得其和为零。
面临着严峻的气候变化带来的问题,作为负责任的国家,中国正脚踏实地进行双碳实践。《第三次气候变化国家评估报告》显示,百余年来(1909—2011年)我国陆地区域平均温度增加0.9~1.5℃,目前處于近百年来气温最高阶段,自然灾害风险等级处于全球较高水平。气候变化对我国的影响利弊共存,总体上弊大于利。2007 年6月3日,中国政府发布了《中国应对气候变化国家方案》,明确了到2010年,我国应对气候变化的具体目标、基本原则、重点领域及其政策措施。中国计划2030年左右二氧化碳排放达到峰值,并计划到2030年非化石能源占一次能源消费比重提高到20%左右。同时中国积极参与清洁发展机制项目,截止到2015年5月5日,国家发展改革委共批准CDM项目2073个,估计年减排量为78 162万吨二氧化碳当量。
用一个简单的词表示双碳,主要就是碳减排。由于以二氧化碳为代表的温室气体的排放引起的气候变暖正在全球范围内产生深远影响,从长远来看,全球变暖产生的损失将远远超过控制温室气体排放(从而抑制全球变暖)的措施所需的费用。通过碳减排减少因人类现代生活所产生的二氧化碳和其他温室气体对环境和气候的影响,特别是全球变暖的问题势在必行。
但是,气候变化的成因和效果都是全球性的,而温室气体的排放又与各国的经济活动紧密联系,因此减排需要全球一体的合作。在全球开展统一的气候变化行动是有效和公平地应对气候变化的基础。全球合作共同防御气候变化给人类带来毁灭性影响,越来越成为人们的共识。而在这个行动中,从百姓的低碳生活到政府的减排承诺,从企业的环保措施到国际磋商协议,人们为此正在艰难地努力。
我们知道,减排不是一句口号,更是一种科学的行动,也意味着我们要放弃一些已经享受到的技术发展带给我们眼前的方便、快捷和舒适。减排也表示着我们要投入一些并不是马上能看到效果的项目,从而影响到经济效益。这就是为什么碳减压力和困难是巨大的原因。如何能找到平衡,一方面尽可能地低碳、最大可能地减排;另一方面又尽可能减少我们的生活影响,达到一定的经济效益,就是我们关心的事。而这正是数学所擅长的。
在这场实现“双碳”目标的变革中,数学将扮演非常重要的角色。
恩格斯说:“任何一门科学的真正完善在于数学工具的广泛应用。”双碳是一个新兴的领域,前期它还停留在教育、政策、法律和技术的层面,但随着其脚步,数学必然将在各个方面展现其巨大的能力,使得双碳行动更科学、更有效地发展。这里要用到的数学工具几乎涵盖了数学的各个分支,从数学建模到统计、计算和模拟方法、运筹学、数学分析、泛函、微分方程、最优控制等。而对数学工作者来说也是一个巨大的挑战:碳减排将提出许多有深度有难度的数学问题,等着数学工作者去解决,同时,如何将现有数学知识应用到碳减排具体工作中,也有一条艰难而漫长的路要走。随着计算机、大数据、人工智能的发展,对数学的要求也越来越多,越来越深,越来越紧迫。更多的数学应用领域将会开发出来。所以对应用数学来说,碳减排是一片丰润的土壤,有待数学工作者、碳排第一线的科技工作者去开垦、去耕耘,也期望着在这个领域可以收获丰硕的成果。
尽管双碳领域很新,数学在这里的应用不只是其中技术层面关键的一部分,也是决策和管理的重要依据。它可以帮助人们理解碳排放的原理,利用碳市场的功能处理相关数据、优化碳减排的过程等。尤其在今天大数据和计算机的时代,数学模型的角色更是不可或缺。
在这个专题中,具体阐述一下数学在双碳中是怎样起作用的,重点谈谈碳计算和碳管理、碳金融、碳优化,以及与数学相关的其他双碳问题。
碳计算是双碳数学中的基础问题,主要有碳排放量、碳吸收量、碳减成本等。
碳排放量
从碳达峰的定义就可以看出,有一个基本量是需要计算的,这就是二氧化碳排放量。计算碳税自然要以计算碳排放量为基础。工业生产和现代生活产生的大量二氧化碳,大多数都排放到了大气中,形成了温室效应。如何计算、如何监督,有技术问题更是数学问题。排放量的计算从理论上来讲并不很难,但实际中的情况千变万化,难以简单统一用一个公式或用一种仪器测定。
最基本的碳排放量计算,目前主要是通过消耗化石能源中的含碳量来计算的。例如开了一千米某种型号的车,烧掉了多少汽油,其中排放了多少二氧化碳,这是客观的值,通过仪器测量或者直接计算就可以得到答案。但各行各业的碳排行为复杂许多,对企业来说,不同的能源、不同的设备、不同的产品、不同的技术,碳排放量都不相同,非常繁杂。至少企业可以雇佣专业人员专门计算测量。而对普通百姓来说,如果想支持双碳行动,会感到不知从何入手,所以让大众明白的最好方法就是对碳排进行量化和可视化。让老百姓明明白白地“看见”自己的行为排放了多少碳,从而节制自己的超排行为。这么说来,如何方便地测量二氧化碳排放量还是有很大的工作空间的。还有很多碳排放的计量并不是那么直接简单,例如,采用了一项新技术,改善了环境,方便了操作等,肯定是减碳了,但减了多少,绕了好几个弯,不是很好算。事实上,目前大量的这种问题都没有解决好,需要数学很大的工作量。
碳吸收量
碳中和不仅要计算碳排放,还要计算碳吸收。如果说碳排是正的排放量,碳吸收就是负的排放量。狭义的碳吸收是指通过技术手段将游离的二氧化碳等温室气体固化,并储存起来。这些技术目前还在发展,还不足以消化生活中的碳排。广义的碳吸收包含我们所熟知的绿化等所有能吸收二氧化碳的手段。
碳吸收的计算比碳排放更困难。就拿种树来说,大家都知道,种一棵树可以吸收一些二氧化碳,可是这个吸收量和树的生长阶段、所处环境、季节时间、天气状况以及树的品种都有关系。所以要做多大的投资,造多大的林,才能通过科学管理达到抵消碳排的目的,也就是说碳中和里的碳吸收的合理计算是必不可少的。
碳减成本
要让碳达峰早日到来,就要减排,那么就要计算减排成本,让实施碳减的人明明白白知道自己将花多少钱。这也是一个相当复杂的计算,不仅要看直接的设备和人员成本、专利价值、边际效益、投资周期、技术红利等,还要看未来的影响和发展。这是一个计量经济学的问题。例如,一个企业要进行碳减,就会带来几个问题:首先要投入一笔钱去购买减碳设备和技术,这势必增加了生产成本,但不行动就会被罚超标的碳排;对不同的碳减技术,如何选择?随着时间,技术会不断改进优化,太早引进,失去了引进更好技术的机会,太晚引进,就必须为引进之前的碳排买单。这些问题都可转变成数学中的优化控制问题,可通过数学方法加以解决。
综上,在碳计算中,数学中的数学模型、数值实验、概率统计、回归分析、数据处理、蒙特卡洛模拟及其他数学方法都将非常有用。
碳管理主要指与双碳相关的管理工作。对于双碳这个新的领域,管理的很多问题都是新的,尚待解决。包括宏观管理(制定和执行政策法律、教育大众等,以保证国家对国际社会的承诺)、微观管理(执行碳减政策、落实碳减手段、推广碳减技术等)。其中微观管理是数学的主要舞台。当然,管理的目的还是控制碳排,鼓励碳减。
碳减的宏观管理
双碳的核心是碳減排。碳减排除了鼓励人们低碳生活、绿化环境外,还可通过另外两种手段来达到目的,即课以碳税和进行碳排放交易。
碳税以减少温室气体排放为目的,以化石燃料(煤、石油、天然气)的含碳量或碳排放量为基准征收税费。碳税的合理计算也是数学的范畴,其可以基于前面所说的碳排放的计算加上政策、法律和行政管理来完成。
碳排放交易就是通过制定一定时间和空间内的碳排放控制目标,将其转化为碳排放配额分配给各级政府和各类企业,并允许政府和企业交易其排放配额,形成二级市场。而碳排放交易的管理有赖于碳市场的管理。
碳配额的分配
这是一个不同于金融市场的管理问题,就是政府方面如何合理地进行碳配额的分配。政府要好好利用手中的分配权,鼓励企业进行碳减,以起到引导作用。碳配额是政府根据其承诺,发放给企业的限额碳排放权。除了这个许可,企业可以通过市场进行调节。而这个配额的合理分配需要通过数学计算进行科学管理。例如,政府手中有一批碳许可量要分配给三个发电厂,如何合理分配呢?分配方案要考虑许多因素,如规模、产量、减排能力、技术力量、历史业绩等。简单地按发电量分配显然起不到鼓励减排的作用,而要考虑众多的因素,科学的方法有很多,其中重要的数学方法就是沙普利(Shapley)分配法和层次分析法。
合理规划碳活动
对于人们平常的各种活动,合理安排计划使之进行低碳活动。如果你要进行一次活动,采取如何的策略,才能使既达到目的又能排放最少的碳。如你要去某地办事,交通工具可选飞机、火车、公汽、自驾、共享车等,在时间限制的前提下,用或者分用什么样的交通工具才是碳排最少。数学中的线性规划可以很有效地处理这类问题。随着人们碳控意识越来越强,规划碳活动的方法的需求量也越来越大。
科学调度碳资源
与碳减有关的资源是有限的,如何调度碳资源、碳设备和碳相关工作人员,使得达到碳减的优化目标,这些都可以用到数学中的数学规划和变分法。例如,政府现在只有50个碳技术员,这些人面临制定碳政策、培训碳新人、研究推广碳技术、检查碳排宣传、双碳意义等工作,如何把好钢用在刀刃上,这就需要用到数学中运筹学的优化分配技术。在管理方面,数学中运筹学、图论等学科的方法是很好的工具。
[1]梁进,杨晓丽,郭华英. 碳减排数学模型与应用. 北京:化学工业出版社,2020.
关键词:碳减排 碳达峰 碳中和 碳计算 碳管理 ■

